Плоское напряженное состояние
Плоское напряженное состояние
Напряженное состояние, когда нормальные напряжения возникают как в направлении оси Х, так и оси Y (например, в тонкостенных сосудах нагруженных внешним давлением). А в сечениях, перпендикулярных осям X и Y действуют касательные напряжения (в балках при изгибе) называется плоским (двухосным) напряженном состоянием.
Покажем, что в плоском напряженном состоянии находится, например, плита (или пластина) произвольной формы с толщиной малой по сравнению с прочими размерами. По контуру плиты действует любая взаимно уравновешенная система внешних сил, распределенных равномерно по толщине и параллельных срединному слою. Вследствие малости изменением напряжений в направлении, перпендикулярном к наружным плоскостям плиты, можно пренебречь. В то же время, т.к. внешние силы на наружных плоскостях отсутствуют, то любой элементарной площадке этих поверхностей усилий и напряжений равны нулю, а следовательно, они равны нулю, и для всех сечений, параллельных этим поверхностям. Эти сечения являются главными, поэтому в рассматриваемом случае одно из главных напряжений равно нулю.
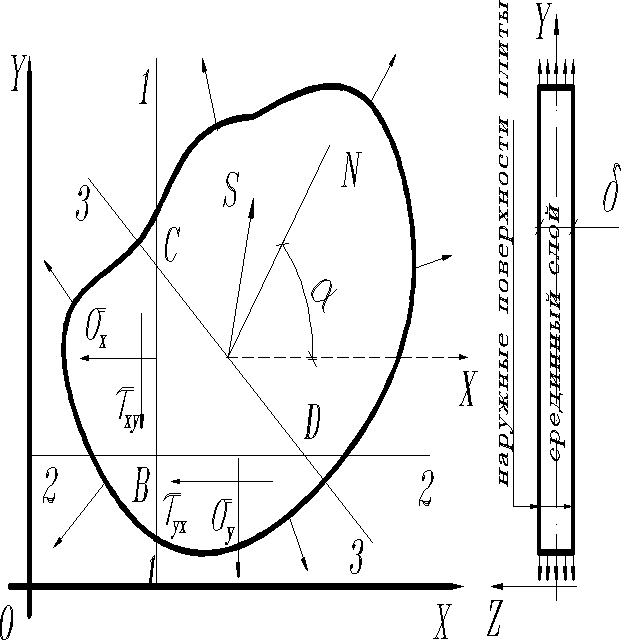
Отнесем тело к координатным осям XOY, расположенным в плоскости срединного слоя. Мысленно рассечем плиту (пластину) сечениями I и II, перпендикулярными осям X и Y. Действие отброшенной части на оставшуюся, вблизи точки B будет представлено напряжениями (напоминаем, что первый индекс для касательных напряжений соответствует оси нормальной к сечению, второй- оси параллельно которой направлено касательное напряжение). Таким образом в общем случае вблизи произвольной точки плиты создается плоское напряженное состояние, при котором .
Напряжения в наклонных сечениях
Поставим задачу: Определить напряжения в произвольном сечении, проходящем через заданную точку B плиты.
Для этого проведем сечение III бесконечно близко от точки B. Полное напряжение в этом сечении можно считать равным полному напряжению в сечении, проходящем через точку B. Положение сечения определяется углом , который составляет с осью X нормаль N к сечению.
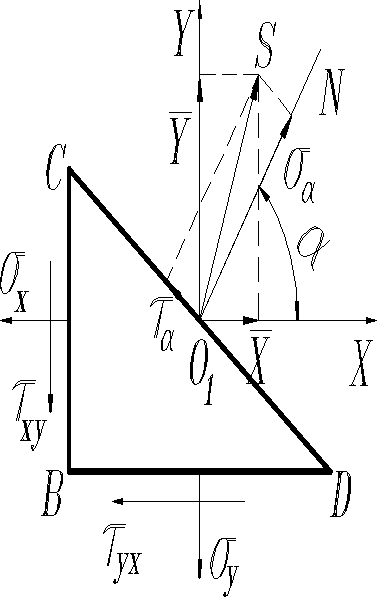
Мысленно выделим из плиты треугольную пластину BCD находящуюся, как и все тело в равновесии. В Виду бесконечно малых размеров пластинки полагаем напряжения равномерно распределенными по граням. Тогда равнодействующая сил, действующих на каждую грань пластинки, может вычисляться, как произведение напряжения на площадь соответствующей грани и будет приложена к центру тяжести грани. Поместим начало координат в точке -центр тяжести грани CD.
Считаем, что напряжения известны. Найдем - составляющие полного напряжения S по координатным осям, а также нормальные и касательные напряжения на грани CD. Составляем уравнения равновесия:
- Сумму моментов относительно точки
После сокращения получим
(1)
Этот результат выражает условие равновесия касательных сил во взаимно перпендикулярных сечениях в непосредственной близости прямого угла, касательные напряжения имеют равные модули и направлены к вершине прямого угла (или от вершины, когда направлены в стороны, противоположные показанным на рисунке).
Обозначим , тогда , , где , -направляющие косинусы.
Уравнения проекции
После сокращения на A
(2)
Найдем нормальную и касательную компоненты полного напряжения
Учитывая, что , , получим
(3)
Можно показать, что:
- - во взаимно перпендикулярных сечениях сумма нормальных напряжений постоянна, а модули касательных напряжений равны;
- - в параллельных сечениях нормальные и касательные напряжения равны по модулю и знаку.
Правила знаков:
- положительные:
-нормальные напряжения , если растягивающие;
-касательные напряжения , если создают вращения элемента BCD относительно точки внутри него против часовой стрелки, а -по часовой стрелки.
Главные напряжения и сечения
Сечения называются главными, если:
- нормальные напряжения достигают экстремальных значений;
- касательные напряжения отсутствуют (равны нулю).
При этом, каким из признаков пользоваться - безразлично, один из них всегда может представлен как следствие другого.
Определим положение главных сечений по второму признаку, полагая, что сечение CD главное, т.е. , а , следовательно
, (а)
Подставив (а) в (2) получим
(4)
Здесь - определяют положение грани CD, когда она становится главным сечением. Система (4) относительно неизвестных является однородной и имеет решение отличное от нуля, только когда определитель системы (4) равен нулю (теорема Руше), т.е.
(5)
В развернутом виде , а после преобразований
(6)
Решая квадратное уравнение, находим модули главных напряжений
, откуда
(7)
Оба корня (7) уравнения (6) являются вещественными, они и дают значения двух главных напряжений и , а третье как отмечалось ранее, в плоском случае напряженного состояния равны нулю. Если , то , то в соответствии с условием , получим , , .
Главные напряжения и , т.е. корни уравнения (6) определяются характером напряженного состояния, и не зависит, от того какая система координатных осей была принята в качестве исходной. Следовательно, при повороте осей X, Y коэффициенты и уравнения (6) должны оставаться неизменными (что ). Поэтому называются инвариантами напряженного состояния.
Найдем направление главных напряжений, или - направляющие косинусы, определяющие положение главных сечений, полагая и вычисленными из выражений (7).
Для этого имеется система уравнений (5), но она однородная и корни её, отличные от нуля, определить невозможно. Из курса тригонометрии известно
(8)
Теперь к уравнению (8) прибавить какое-нибудь из системы (5), например первое
(в)
то получим систему уравнений (8) и (в) неоднородную и определенную, решая которую и установим положение главных сечений.
Подставив в (в) вначале будем иметь
(с)
-косинусы углов, которые составляет с координатными осями X и Y нормаль к первому главному сечению, что те же главные напряжения .
Решая систему уравнения (с) получим
(9)
Таким же образом, подставив в (в)
(10)
В (9) и (10) - углы отмеряемые вращением против хода часовой стрелки от оси X до нормалей к сечениям, в которых действуют соответственно главные напряжения и .
Установим положение главных сечений по отношению друг к другу. Для этого, перемножим почленно уравнения (9) и (10)
(d)
При подстановке в (d) значений и из (7) после преобразований приходим к следующему выражению
(е)
Т.к. , то можно написать . Значить
. Отсюда следует, что главные сечения взаимно перпендикулярны, а и (9’), (10’)
Заметим, что сложив обе строки формулы (7), будем иметь -во взаимно перпендикулярных сечениях сумма нормальных напряжений постоянна.
Главные деформации
Определим деформации в направлении главных напряжений. Для этого мысленно выделим из тела, находящегося в плоском напряженном состоянии прямоугольный элемент, грани которого параллельны главным сечениям. Т.к. по граням действуют только нормальные напряжения, то направления главных напряжений будет совпадать с деформациями, называемыми главными. Используя формулы обобщенного закону Гука и полагая , получим
(11)
Экстремальные касательные напряжения
Предположим, что по граням BC и BD треугольной пластинки BCD действуют главные напряжения и . Тогда и выражения (3) примут вид
(k)
(m)
Исследуем функцию (m) на экстремум, исходя из условия существования . Дифференцируем (m) по .
В общем случае , следовательно (s).
Значок при поставлен для того, чтобы отличить корни уравнения (s), определяющие положение сечений, в которых достигает экстремальных значений, от корней уравнений (9), (10) определяющих положение главных сечений.
Уравнение (s) в пределах имеет два корня, отличающихся друг от друга на и , откуда получаем .
Т.о. сечения в которых касательные напряжения достигают наибольшего абсолютного значения, располагаются под углом к главным сечениям. Эти сечения также взаимно перпендикулярны.
При и выражение (k0 принимает вид
(12)
В этих же сечениях
или (13)
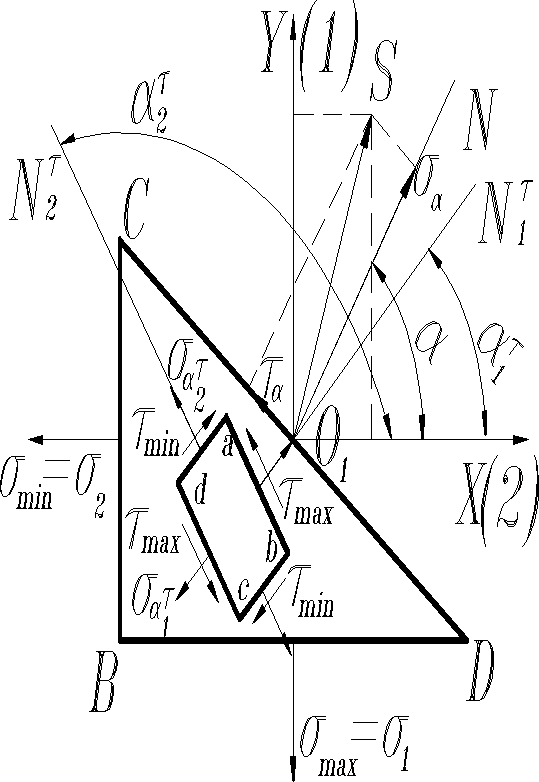
На рисунке и в дальнейшем отсчет углов ведется от оси (2 или 3), совпадающей по направлению с наименьшим из главных напряжений ( или ). Тогда, в соответствии с изложенным, под углом к этой оси располагается нормаль к сечению с , а под углом - с . На гранях пластинки abcd, кроме касательных напряжений могут быть и нормальные , определяемые по формуле (13). Заметим, что всегда больше нуля и поэтому имеет направление, при котором создает вращение элемента abcd относительно любой точки внутри него против часовой стрелки, -по часовой стрелки. В общем случае плоского напряженного состояния , когда заданы не главные напряжения, а и модули экстремальных можно определить по формуле
(14)
которые получены при подстановке (7) в (12).
Удельная потенциальная энергия
При растяжении (сжатии) внешние силы совершают работу вследствие перемещения точек их приложения и вызывают деформации материала. При деформации совершают работу и внутренние силы упругости. Известно, что энергия, накопленная телом при деформации, называется потенциальной энергией деформации, а величина этой энергии, отнесенная к единице объема материала – удельной потенциальной энергией . При центральном растяжении (сжатии) вычисляли из выражения . В плоском напряженном состоянии удельная потенциальная энергия деформации получится как сумма двух слагаемых
, т.к. и , тогда
(15)
Плоское напряженное состояние