Объемное (пространственное) напряженное состояние
Объемное (пространственное) напряженное состояние.
Известно, что напряжения в сечениях, проходящих через заданную точку нагруженного тела, зависит от ориентации сечения в пространстве. С поворотом сечения меняются и напряжения. Совокупность напряжений, возникающих во множестве сечений, проходящих через рассматриваемую точку, называется напряженным состоянием вблизи точки. Оно поддается анализу не только в частных случаях чистого растяжения, сдвига и плоской задачи, но и в случае нагружения тела силами, произвольно направленными в пространстве.
Исследование законов изменения напряжений вблизи точки не является чисто отвлеченным. Оно необходимо для последующего решения сложных задач, и в первую очередь для расчетов на прочность в общих случаях нагружения. Примером объемного напряженного состояния может служить сопротивление материала при передачи давления от шарика на обойму в подшипнике или от колес подвижного состава на рельсы.
Содержание настоящей темы справедливо для любого сплошного тела.
Напряжения в произвольном сечении.
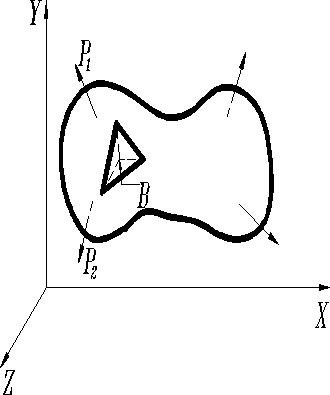
Рассмотрим произвольно нагруженное тело, отнесенное к системе координатных осей XYZ. В окрестности точки В мысленно выделим бесконечно малый тетраедр BCDE, у которого три грани параллельны координатным плоскостям, а четвертая CDE имеет ориентацию, характерной нормалью N с направляющими косинусами , , , т.к. тетраедр бесконечно мал, то в пределе все четыре грани можно считать проходящими через точку В. Начало координатных осей поместим в точку - центр тяжести CDE.
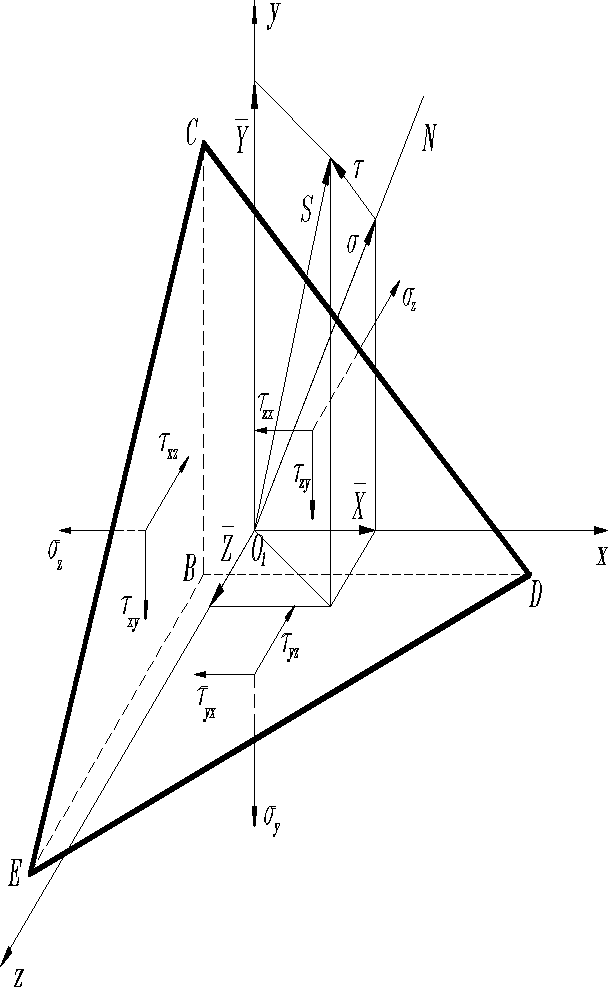
Действие окружающего тела на тетраедр заменим внутренними силами. Интенсивность этих сил есть напряжения. При этом на гранях, параллельных координатным осям, полное напряжение направлено тремя составляющими: нормальным и двумя касательными напряжениями, в значки которых расставлены в соответствии с правилом, изложенным ранее. Проекции на координатные оси вектора полного напряжения S в сечении общего положения CDE обозначим через X, Y, Z, составляющие S на нормаль N и перпендикулярно ей – через и .
Поставим задачу: Найти
Запишем суммы моментов всех сил относительно координатных осей.
(в это уравнение не вошли силы, параллельные оси Z, и силы, линия действия которых пересекают эту ось).
После сокращений получаем
или (1)
Аналогично из и соответственно будем иметь
, (1)
Три уравнения (1) выражают закон равновесия касательных сил: в двух взаимно перпендикулярных сечениях составляющие касательных напряжений, перпендикулярных к общему ребру равны по модулю и направлены либо к ребру, либо от ребра. Это справедливо для всех точек напряженного тела, независимо от вида приложенных нагрузок и свойств материала. Следствием является то, что на взаимно перпендикулярных гранях выделенного тетраедра имеем не девять, а только шесть независимых компонентов напряжений.
Для записи уравнений проекции всех сил на координатные оси удобно ввести следующие зависимости между площадями граней тетраедра. Обозначим площадь грани CDE через А, а так как грани BCD, BDE, BCD являются проекциями грани CDE на соответствующую координатную плоскость, то , , .
Проектируя усилия, действующие по граням тетраедра на ось Х, получим
; Откуда
(2)
Подобным образом, из уравнения и
(2)
Полное напряжение S определим как диагональ параллелепипеда, построенного на . Значит
(3)
Составляющая S на нормаль N равна
(4)
или как сумму проекций на N компонентов напряжения S
(5)
Подставляя (2) в (5) получим
(6)
И, наконец, для касательного напряжения получим
(7)
Т.о. формулы (2)-(7) позволяют найти полное напряжение S и его составляющие , в любом сечении, проходящем через точку тела и определяемом направляющими косинусами , если известны шесть компонентов напряжений вблизи этой точки . Иными словами: напряженное состояние вблизи точки определяется шестью компонентами, называемыми компонентами тензора напряжений, а совокупность напряжений во всех сечениях, которое можно провести через точку – тензором напряжений . Тензору в отличие от вектора, определяемого тремя величинами, не может быть дано простого геометрического толкования и его обычно задают матрицей (таблицей), написанный в виде
(8)
Если взамен исходной системе осей X, Y, Z выбрать новую систему, компоненты изменятся, т.е. значения будут иными. Однако тензор напряжений остается тем же. Поясним на примере.
Вектор определен матрицей, членами которой являются координаты конца вектора :
- 0 60). Если перейти к системе X, Y, Z, то для того же вектора получим (100 0 0).
Компоненты вектора изменились, но сам вектор остался неизменным.
Существование главных сечений. Эллипсоид напряжений.
Пусть через точку В напряженного тела проходит сечения с нормалью N , направляющие косинусы которой . Отложим вдоль нормали вектор . Под радикалом используется знак плюс, если и знак минус, если ;
Главные напряжения и главные сечения.
Пусть вблизи некоторой точки напряженного тела известны компоненты тензора напряжения . Требуется определить главные напряжения и положение главных сечений.
Положим, что одно из наклонных сечений является главным. Тогда и вектор полного напряжения S сольется с вектором , т.е. расположится вдоль нормали N к сечению, и, следовательно
, , (а)
Подставив (а) в (2) и приводя подобные члены, получим
(9)
Система однородных уравнений (9) относительно направляющих косинусов определяющих положение главных сечений, имеет решение отличное от нуля при условии
(10)
Раскрывая определитель (10) и используя условие равновесия касательных сил, получаем следующее кубическое уравнение
(11)
где (12)
Уравнение (10) имеет три вещественных корня .
Они и дают три значения главных напряжений . Коэффициенты остаются неизменными при повороте координатных осей и называются инвариантами напряженного состояния.
Для нахождения направляющих косинусов определяющих положение главных сечений, необходимо поочередно подставить , , в какие-нибудь два уравнения (9) и решить их совместно с получив совместно .
Главные деформации и закон Гука.
Относительные деформации в направлении главных напряжений называются главными деформациями и вычисляются по формулам
(13)
Покажем, что - это наибольшая относительная деформация, которая может иметь место вблизи точки.
Введем в правую часть первого уравнения системы (13) очевидный нуль :
(14)
и по аналогии получим
(14)
где .
Т.к. в общем случае , то из анализа выражений (14) приходим к заключению , что и требовалось доказать.
При одновременном действии нормальных и касательных напряжений обобщенный закон Гука будет представлен формулами
(15)
Экстремальные касательные напряжения.
При расчете прочности материала, важную роль играют наибольшие касательные напряжения.
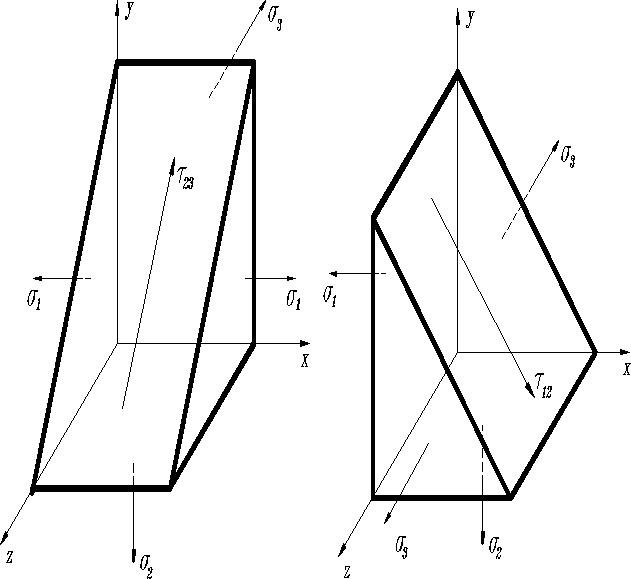
Допустим, что три взаимно перпендикулярные грани тетраедра являются главными, а главные напряжения известны. Запишем выражение для касательного напряжения 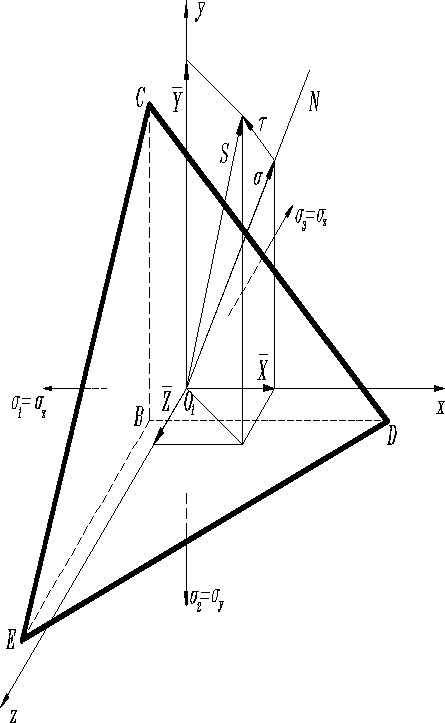
на наклонной грани CDE, т.к. , то уравнения (2), (3) и (5) примут вид
(а)
(в)
Подставив (а) и (в) в (7)
(с)
Уравнение перепишем относительно и подставим полученное значение в (с) представив касательное напряжение на грани CDE как функцию двух переменных
(d)
В связи со сказанным, условием существования экстремума будет
и (е)
Дифференцируя (d) по , учитывая условие (е) и полагая в общем случае , после преобразования перейдем к уравнениям
(f)
(g)
которые распадаются на следующие
(h) ; (i)
(j) ; (к)
Очевидно, подлежат рассмотрению 4 варианта:
- , . Тогда , . Это сечение перпендикулярное к оси Z , но в нем , и следовательно, первый вариант не приносит экстремальных касательных напряжений.
- Одновременно удовлетворяются уравнения (i) и (k). Вычитая (к) из (i) получаем , а это возможно только как частный случай, т.к. решение ведется в предположении, что . Значит, этот вариант тоже отпадает.
- Одновременно удовлетворяются уравнения (i) и (j). Тогда подстановка (j) в (i) приводит к , а из находим .
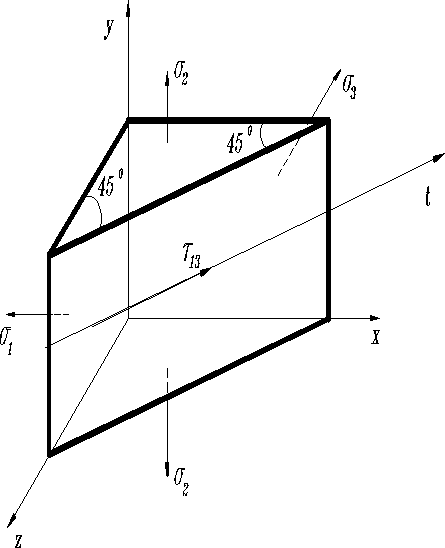
Очевидно, что направляющие косинусы , определяют сечение, расположенное параллельно оси Y и под углами 450 к осям X и Z. Касательные напряжения в этом сечении найдем подставив , в (с):
(16)
Это и будет одно из экстремальных значений касательных напряжений. Направление определим из уравнения проекций сил на оси, приложенных к призме:
Откуда при получаем , значит, придано верное направление (от большого главного напряжения к меньшему ).
- Удовлетворяются уравнения (h) и (k). Повторив решения выполненное при рассмотрение третьего варианта, будем иметь
(17).
И, наконец, выразив или через два других направляющих косинуса, представив , как функцию и или и , проделав решение, подобные приведенному выше, найдем третий экстремум
(18).
Т.к. касательные напряжения достигают экстремальных значений в сечениях, наклонных к главным под углом 450, и равны полуразности тех главных напряжений, линия действия которых пересекают сечения. Наибольшим касательным напряжением, при условии является .
Заметим, что в сечениях с экстремальными касательными напряжениями есть нормальные напряжения , вычисляемые по формуле (в).
Удельная потенциальная энергия деформации.
Предполагая постепенное возрастание главных напряжений и пользуясь принципом суперпозиции, подсчитаем удельную потенциальную энергию, как сумму энергий от действия каждого из по формуле
(19)
или с учетом (13)
(20)
Удельная потенциальная энергия деформации может рассматриваться как состоящая из двух частей:
- Энергии , накапливаемой за счет изменения объема V упругого тела;
- Энергии , связанной с изменением формы тела, т.е
(а)
Такое разделение оказывается удобным при дальнейшем рассмотрении вопроса о прочности материала.
Подсчитаем величины и .
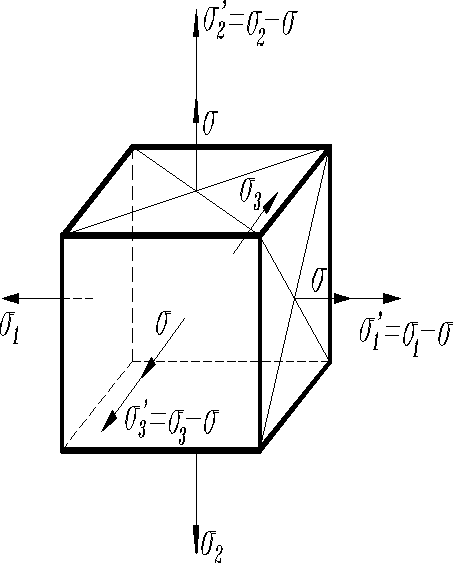
Пусть по граням мысленно выделенного из тела кубика действуют главные напряжения . Разделив векторы этих напряжений на составляющие, изменяющие объем и форму:
- Напряжения , одинаковые по всем направлениям, будут изменять объем;
- Только форму - напряжения , , (в).
Если (в) подставить в выражение относительного изменения объема тела то должны получать ноль, т.е.
В общем случае , поэтому , и, следовательно
(21)
Тогда энергия изменения объема вычисляемая по формуле (19)
(22)
где - относительная деформация при всестороннем действии одинаковых напряжений .
Потенциальную энергию, соответствующую изменению формы выделенного элемента, найдем как разность
После преобразований получим
(23)
При центральном растяжении, когда , , удельная потенциальная энергия формоизменения определится из выражения
(24)
Если напряженное состояние вблизи точки задано компонентами тензора напряжений
, то полная удельная потенциальная энергия деформации вычисляется по формуле
(25)
Выводы:
Показано, что если вблизи точки тела заданы компоненты тензора напряжений, то можно определить полное напряжение и его составляющие в любом сечении, проходящем через эту точку, найти модули экстремальных нормальных и касательных напряжений, а также установить сечения, в которых они действуют, вычислить главные деформации и удельную потенциальную энергию деформации. Многие положения темы справедливы для любого сплошного тела, в том числе и неупругого.
Полученные результаты используются при расчете прочности материала в сложных случаях напряженного состояния.
Объемное (пространственное) напряженное состояние