Геометрические характеристики поперечных сечений
Геометрические характеристики поперечных сечений
Основным объектом, изучаемым в курсе сопротивления материалов, является стержень (брус). Сопротивление стержня различным видам деформации зависит не только от его материала и размеров, но и от очертания оси, формы поперечных сечений и их расположения, которыми являются площадь, положение центра тяжести сечения, статические моменты и моменты инерции площади сечения.
При растяжении (сжатии) – сопротивление стержня пропорционально площади поперечного сечения. Чем больше площадь поперечного сечения, тем меньше напряжения и удлинения стержня или .
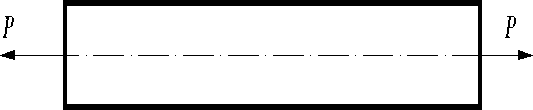
Если сила приложена к стержню перпендикулярно его оси
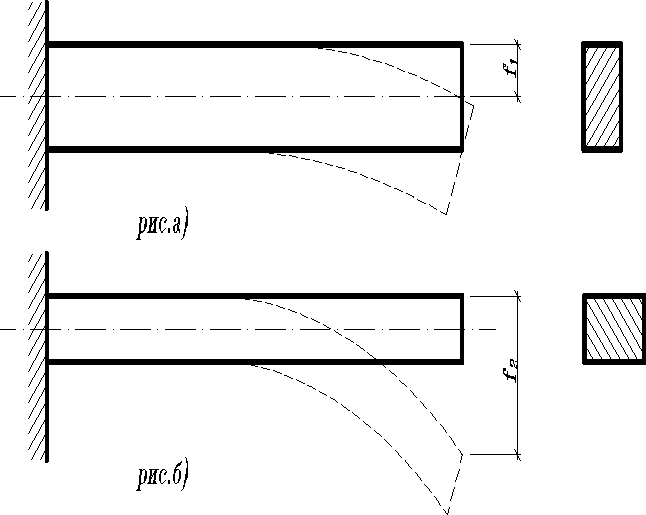
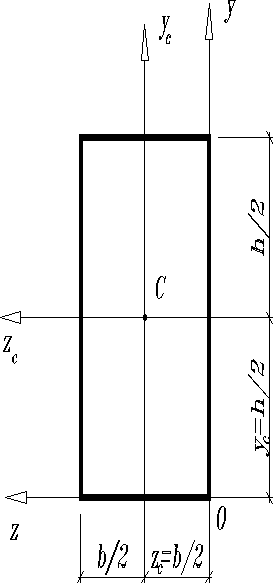
При одной и той же площади в зависимости от ориентировки поперечного сечения (рис. а) и (рис. б) стержень по разному сопротивляется действию силы. Отсюда можно сделать заключение, что площадь поперечного сечения не может характеризовать сопротивляемость стержня изгибу. Оказывается, при изучении изгиба, кручения и других случаев деформации стержня необходимо привлекать более сложные геометрические характеристики сечения. В связи с этим возникает задача об изучении некоторых геометрических свойств различных плоских фигур.
Площадь поперечного сечения стержня
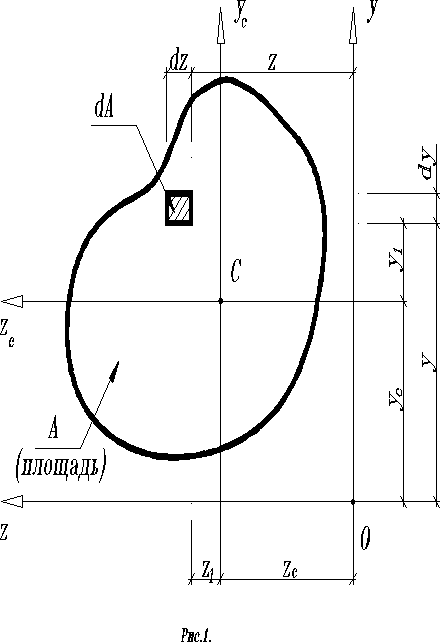
Рассмотрим брус произвольного поперечного сечения. Зададимся системой координатных осей ОХ, ОУ, OZ. Выделим бесконечно малый элемент площадью с координатами y, z. Площадь поперечного сечения бруса будет равна
(1).
Например, в случае прямоугольника получим
.
В инженерной практике часто встречаются сечения, составленные из нескольких частей, каждая из которых имеет простую геометрическую форму. При определении площади такой фигуры необходимо разбить её на составные части и затем воспользоваться суммированием.
Статические моменты плоских фигур
По аналогии с выражением для момента силы относительно какой-либо оси можно составить выражение и для момента площади, которое называется статическим моментом. Так, произведение элемента площади на расстояние от оси OY. - называется статическим моментом элемента площади относительно оси OY. Аналогично - статический момент элемента площади относительно оси OZ. Просуммировав такие произведения по всей площади фигуры, получим статические моменты относительно осей Y и Z
и (2)
Статические моменты измеряются в единицах длины в кубе – см3, м3.
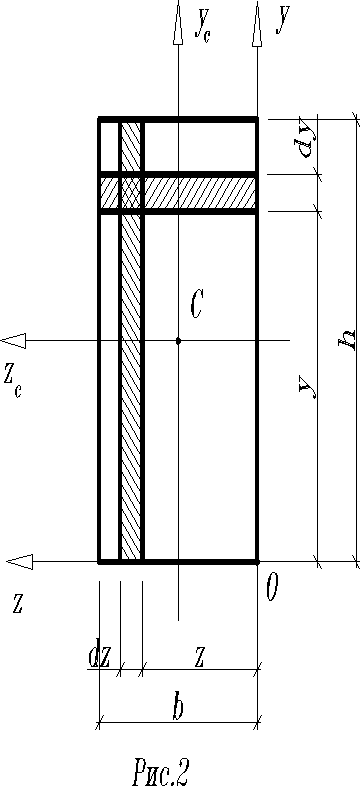
Например, для прямоугольника будем иметь
;
.
Ординаты “y” и аппликата “z” входят в подинтегральные выражения с соответствующими знаками. Поэтому статический момент может иметь знак “+”, “-“ и может быть равен нулю. Ось, относительно которой статический момент равен нулю, называется центральной, а точка пересечения двух центральных осей – центром тяжести фигуры. Задача определения статических моментов плоских фигур значительно упрощается, если известно положение центра тяжести фигуры. Нахождение положения центра тяжести можно проиллюстрировать следующим примером.
Пусть С – центр тяжести фигуры (рис.1), “y” и “z” – координаты элементарной площадки относительно центральных осей и ;
и - координаты центра тяжести фигуры “С” относительно осей ОУ и OZ. Тогда , и
Но и - как статические моменты относительно центральных осей и . Поэтому и (3).
Откуда , (4).
Например, в случае прямоугольника
; .
В случае сложной фигуры
;
и (4) примет вид
(5).
Формулы (5) позволяют определить координаты центра тяжести сложной плоской фигуры, если известно положение центров тяжести составляющих фигур.
Замечания: 1) В случае, когда фигуры разбивается только на две части, её центр тяжести “C” всегда лежит на прямой, соединяющий центры тяжести С1 и С2. В случае, если фигура имеет ось симметрии, то центр тяжести расположен на этой оси.
Осевые, полярные и центробежные моменты инерции плоских фигур. Радиусы инерции.
Осевые или экваториальные моменты инерции площади плоской фигуры относительно осей OY и OZ определяются соответственно выражениями
и (6)
в которых элементарная площадь умножается на квадрат расстояния до соответствующей оси, а интегрирование производится по всей площади . Осевые моменты инерции иногда называются моментами второго рода.
Момент инерции плоской фигуры относительно оси “X”, перпендикулярной плоскости этой фигуры, называется полярным моментом инерции. Он определяется выражением
(7)
где каждый элемент площадью умножается на квадрат расстояния до точки “0” пересечения оси “X” с плоскостью фигуры. Заметив, что , будем иметь
(8).
Отметим, что величины осевых и полярных моментов инерции всегда положительны.
Центробежным моментом инерции называется интеграл произведений площадей элементарных площадок на их расстояния относительно координатных осей OZ и OY
(9)
В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю.
Согласно определению момента инерции (6 9), он имеет размерность длины в четвертой степени – см4, м4. Поэтому при делении осевого момента инерции на площадь получается величина размерностью длины в квадрате. Корень квадратный из этой величины называется радиусом инерции фигуры. Т.о. обозначив радиус инерции через , получим
; (10)
и - соответственно радиусы инерции относительно осей Y и Z.
В случае прямоугольника имеем
;
;
;
;
Зависимость между моментами инерции для параллельных осей
Рассмотрим фигуру произвольного поперечного сечения. Так как , , то (рис.1)
а с учётом, что ; ; , получим
(11).
По аналогии
(12)
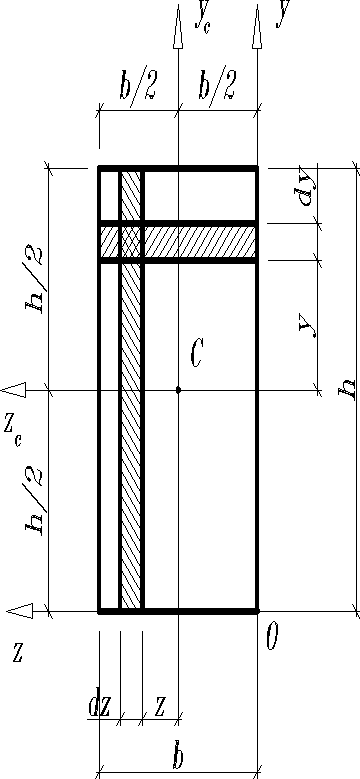
Т.о. если известны моменты инерции фигуры относительно центральных осей её, то момент инерции относительно осей параллельных центральным можно определить из выражений (11), (12). Используя эти же выражения, найдём моменты инерции относительно центральных осей прямоугольника.
.
В случае сложной плоской фигуры, состоящей из нескольких простейших, моменты инерции определяют суммированием
(12’)
Изменение осевых и центробежных моментов инерции при повороте координатных осей
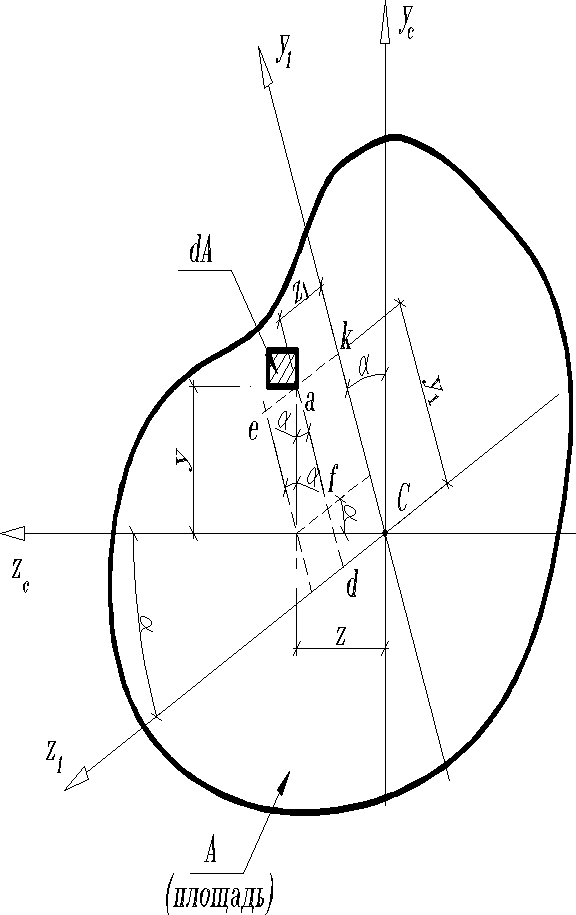
Из формул (12) следует, что изменения моментов инерции достаточно ограничить случаем моментов инерции относительно центральных осей. Имея это в виду, и принимая начало координат в центре тяжести фигуры “C”, найдём моменты инерции относительно осей CY1 и CZ1, повернутых по отношению к первоначальным осям CY и CZ на угол . Угол считается положительным, если отложен против часовой стрелки.
Выражения для моментов инерции
;;
;.
Координаты площадки в системе повернутых осей по формулам преобразования координат при повороте осей имеем , и, следовательно,
Т.о. (13)
По аналогии
(14)
(15)
Иногда выражения для и записывается в другом виде, путём подстановки
и
Аналогично
Сложив (13) и (14) получим . Т.е. сумма моментов инерции относительно двух взаимно перпендикулярных осей постоянна (инвариантна) к повороту осей. Видим, что моменты инерции и центробежный момент являются непрерывной функцией угла поворота .
Главные оси и моменты инерции.
Определим экстремальные значения момента инерции , исходя из условия существования экстремума функции . Для этого возьмём производную по х от выражения (13) и приравняем её нулю.
или
(а)
Разделив (а) на , найдём (16)
Уравнение (16) имеет два корня: I-ой и III-ей четверти положительные, в двух других (I и IV) - отрицательные. При этом один корень отличается на , т.е. . Т.о. моменты инерции достигают экстремальных значений относительно осей, расположенных под углами
и . Оси, относительно которых моменты инерции достигают экстремальных значений, называются главными осями инерции. Таких осей две и они взаимно перпендикулярны ( и ).
Найдём модули экстремальных моментов инерции, называемыми главными моментами инерции. Для этого в выражение (13) подставим , ,
и затем вместо
(в)
Для получения экстремальных значений , в выражение (в) подставим (16). Тогда
Откуда ; (17).
Для определения относительно какой из осей момент инерции максимальный и относительно какой минимальный, продифференцируем (13) два раза по
(18)
Если при подстановке в (18) , , и получим , то под углом расположена ось, относительно которой момент инерции максимальный ; и наоборот при под - .
Замечание I. Центробежный момент инерции относительно главных осей инерции равен нулю. Действительно, из (15) имеем
Подставив в последнее выражение вместо его значение из (16) получим
Замечание II. Главные центральные оси инерции являются главными во всех точках. Если к одной из главных центральных осей, например, Yc провести перпендикулярно в произвольном месте ось Z1, то
Т.е. ось Yc остается главной независимо от того в какой точке будет находиться начало координат.
Замечание III. Сложив выражение (17) будем иметь
Т.о. относительно главных осей инерции:
- Моменты инерции достигают экстремальных значений.
- Центробежный момент инерции равен нулю.
Главные оси и моменты инерции могут быть определены для случая начала координат в произвольной точке. Например, для случая, представленного на рисунке при
; ; ;
; ;
При ; При
Эллипс инерции
Главным осям инерции соответствуют главные радиусы инерции, вычисляемые из выражений
; (19)
Для случая представленного на рисунке ; .
Построим на главных осях инерции фигуры эллипс инерции с полуосями, равными главным радиусам инерции. Причем вдоль оси I отложим отрезки , а вдоль оси II - отрезки . Такие эллипсы называются эллипсами инерции.
Главный центральный эллипс инерции находит применение при графическом определении момента инерции относительно произвольной оси, например, “y”. Можно показать, что
(20)
где - кратчайшее расстояние между осью “y” и осью “y1”, параллельной оси “y” и касательной к центральному эллипсу инерции в точке A, наиболее удаленной от оси “y”.
Т.о. достаточно, зная площадь А фигуры и имея чертёж, выполненный в масштабе, определить измерением расстояние , подставив значения А и в (20), найти требуемый момент инерции .
Изложенная теория позволяет определять геометрические характеристики поперечных сечений элементов и использовать их при выполнении инженерных расчётов.
Напишем выражение момента инерции относительно оси W под углом ; - т.к. оси z и y главные.
Уравнение эллипса .
Уравнение касательной к эллипсу (m), которую проведём параллельно оси W;
где и координаты точки касания.
Из чертёжа (d).
Сравнивая (m) и (d), можно сделать вывод ; или ;
подставим в уравнение эллипса инерции
Величина численно равна радиусу инерции относительно наклонной оси. Это позволяет графически определить момент инерции относительно любой оси проходящей через начало координат
Для этого достаточно провести касательную к эллипсу параллельно этой оси и замерить кратчайшее расстояние между касательной и осью. Это расстояние и будет равно радиусу инерции для рассматриваемой оси.
Моменты инерции простых фигур
Прямоугольный треугольник
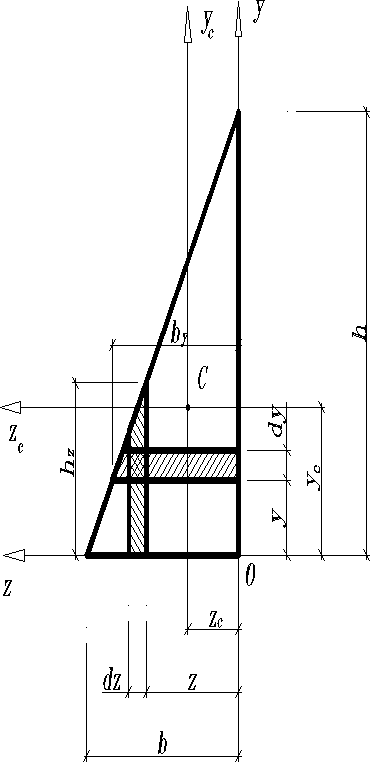
;
;
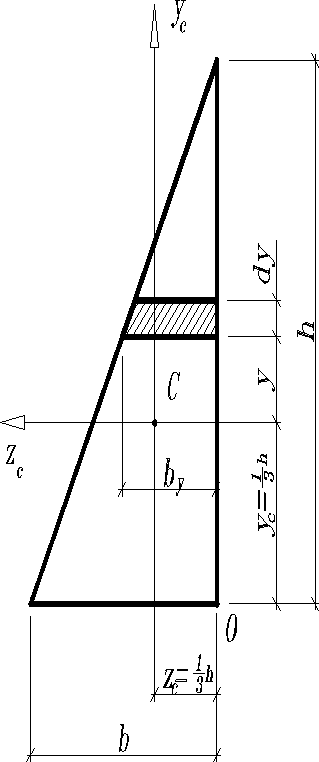
Круг
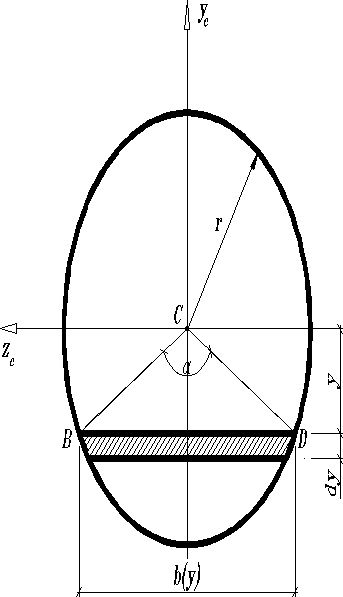
Ширина полоски будет переменной по высоте сечения. Площадь . Момент инерции . Так как верхняя и нижняя половины сечения одинаковы, то вычисление моментов инерции достаточно провести для одной нижней и результат удвоить. Пределами для изменения будут 0 и , тогда . Введём новую переменную интегрирования – угол , тогда ; ; . Пределы при ; при , следовательно
.
II способ. Сначала вычисляем полярный момент инерции.
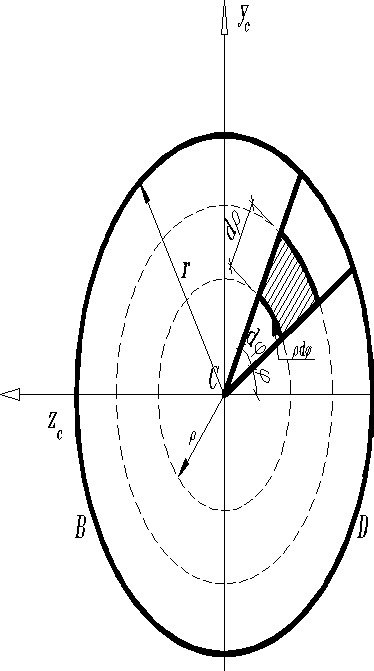
;
;
Учитывая, что полярный момент инерции равен сумме двух осевых моментов, получим
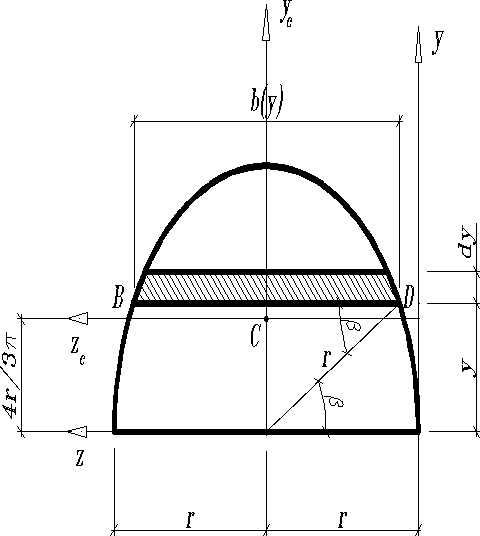
Полукруг
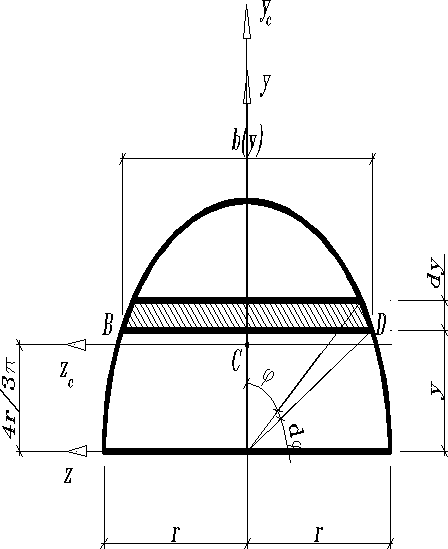
; ; ; .
при изменении от нуля до угол изменяется от до нуля, т.е. при ; при , следовательно:
статический момент
;
координаты центра тяжести
;
;
.
; ; ; .
при изменении от нуля до угол изменяется от нуля до , т.е. при ; при , следовательно:
статический момент
;
координаты центра тяжести
;
;
.
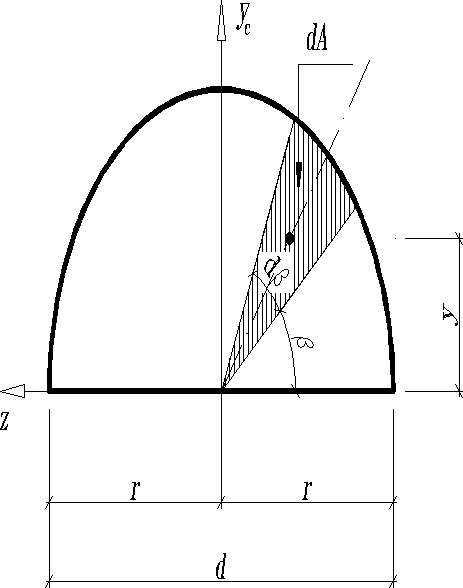
Для определения статического момента полукруга можно разбить его площадь на элементарные сектора. Площадь каждого из таких секторов определяем как площадь треугольника с основанием и высотой , т.е. ;
Ордината центра тяжести ;
Равнобедренный треугольник
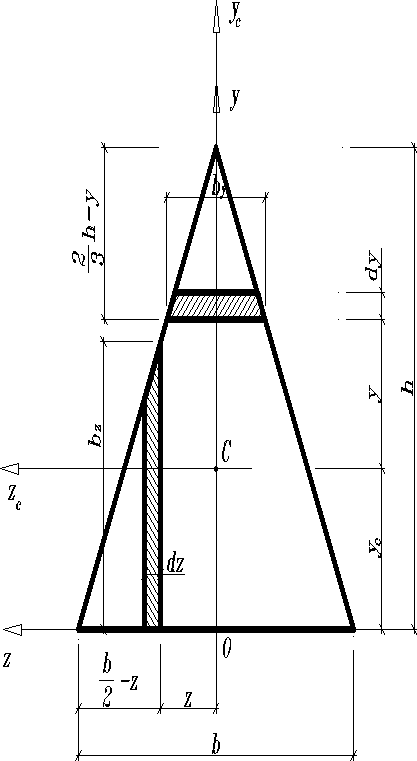
;
;
Кольцо
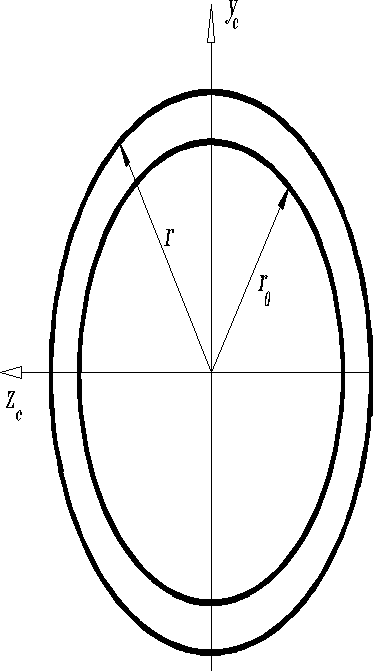
Статический момент половины площади относительно центральных осей
где
или
Тонкое кольцо
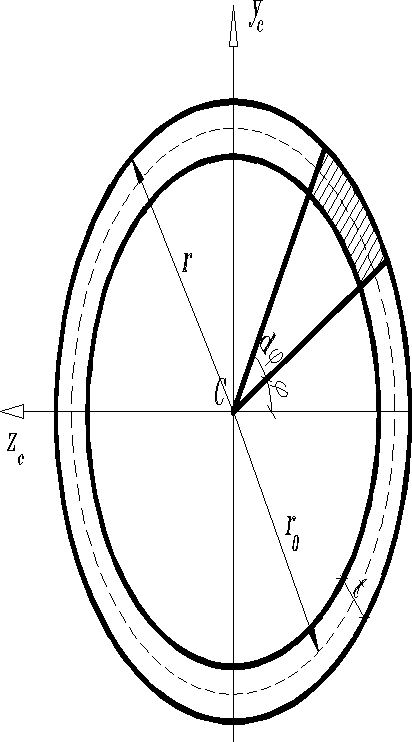
Толщина кольца пренебрежимо мало по сравнению с радиусом . Рекомендуется предварительно подсчитать полярный момент инерции кольца , выразив , тогда
Из курса математики известно:
Статический момент полукольца будет равен разности статических моментов относительно диаметра наружного и внутреннего полукругов
;
Момент инерции
где - средний радиус трубы;
Геометрические характеристики поперечных сечений