Напряжения при плоском поперечном изгибе

Рассматриваются балки, имеющие хотя бы одну продольную плоскость симметрии V. Внешние силы располагаются в этой же плоскости. Направлены по нормали к оси абсцисс Х. Если при чистом плоском изгибе , то при плоском поперечном изгибе на участках балки изменяется по длине бруса. Теперь и нормальные напряжения вблизи сходственных точек поперечного сечения будут различными. Действительно, полагая непрерывными функциями абсциссы Х, получим, что если в сечении действуют , то вблизи точки с координатами y и z возникает напряжения . А в сечении , отстоящем от на расстоянии имеются соответственно -.

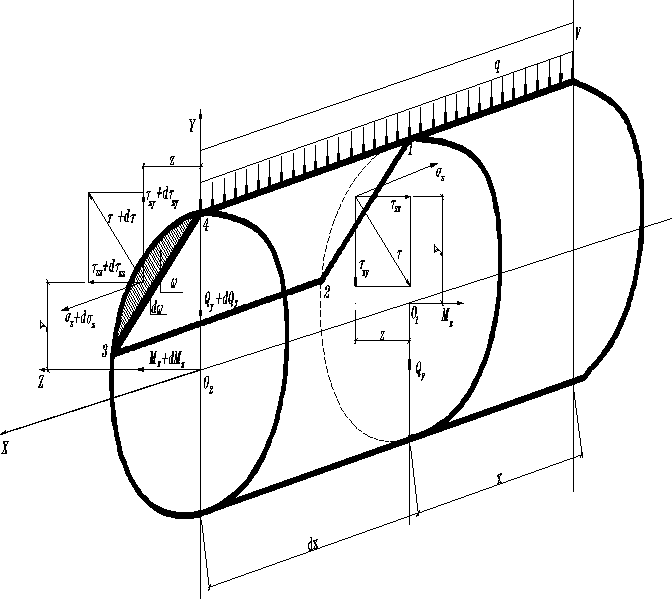
Проводя мысленно произвольное продольное сечение 1234, параллельное оси Х, выделим из балки элемент длиной с площадью торцов . Равнодействующая нормальных сил на дальнем торце , на ближнем . Для обеспечения равновесия элемента по сечению 1234 должно действовать касательное усилие dT, определяемое из условия

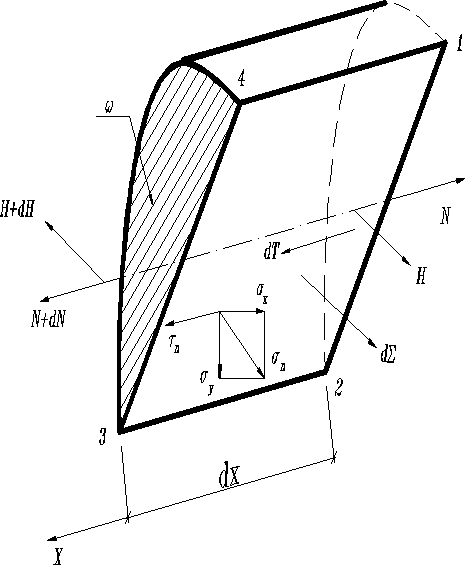
; Откуда

(1)

В результате вблизи произвольной точки продольного, на основании закона равновесия касательных сил, и поперечного сечения возникают касательные напряжения, которое обозначают через (в сечении 1234 –рис.2), ( в сечениях и с компонентами ; (рис.1)). Касательные напряжения вызывают сдвиги, сопровождающиеся угловыми деформациями и приводящими к искривлению поперечных сечений.

На рис2. равнодействующая касательных усилий на дальнем торце представлена величиной H на ближнем . Теперь для обеспечения равновесия выделенного элемента оказывается возможным появление в продольном сечении 1234 нормальных напряжений с компонентами и равнодействующей нормальных усилий .

Следовательно, в общем случае плоского поперечного изгиба балки произвольного поперечного сечения вблизи рассматриваемой точки создается сложное напряженное состояние, и определение внутренних усилий по заданным внешним силам является статически неопределенной задачей, решать которую в сопротивлении материалов приходится приближенно.

Нормальные напряжения

В случае чистого плоского изгиба стержня () нормальные напряжения в поперечных сечениях определяются по формуле

(2)

При , сечение балки плоское до изгиба в результате действия касательных напряжений искривляется. С учетом влияния этого искривления должны быть изменены и выводы о распределении напряжений . Однако исследования, проведенные точными методами теории упругости, и результаты экспериментов показывают, что наличие и сопутствующие им искажения, лишь незначительно изменяют найденные по формуле (2) нормальные напряжения (за исключением особых случаев). Так, например для двухопорной балки прямоугольного поперечного сечения, загруженной равномерно распределенной нагрузкой, ошибка в определении наибольших () по (2) составляет 0,27% и 1,07% при , где - высота и пролет балки. Возникающие в продольных сечениях этой балки составляет от соответственно 1,33% и 5,28%. Приведенные расхождения при вычислении напряжений не имеют практического значения и . Заметим, что если , то элемент следует рассчитывать как пластинку (балку-стенку), применяя метод теории упругости: если поперечная сила на участках балки постоянная, то результаты точного решения и полученные по (2) совпадают.

Поэтому в дальнейшем и при плоском поперечном изгибе нормальные напряжения будем определять по формуле (2). Это равносильно следующим допущениям о том, что:1) поперечные сечения остаются плоскими при изгибе с поперечной силой; 2)давления продольных волокон друг на друга отсутствуют, т.е..

Касательные напряжения

Для решения задач об установления зависимости касательных напряжений от координат точки в поперечном сечений введем третье допущение, сформулированное русским инженером и ученым Д.И.Журавским (1782-1871?) и состоящее в следующем:

вблизи точек сечения, расположенных на линии перпендикулярной плоскости действия внешних сил, значении составляющей полного напряжения параллельной этой плоскости, одинаково. Т.е. в случае компонента является функцией только ординаты y и при .

Основные особенности распределения касательных напряжении по сечению любого вида могут быть выявлены при исследовании в трех формах поперечного сечения балки: прямоугольной, двутавровой и круглой.

а) прямоугольное поперечное сечение

Пусть ширина балки высота и . Требуется найти компоненты полного касательного напряжения вблизи точки с координатой y и построить эпюры при .

На уровне y мысленно проведем горизонтальное сечение. Т.к. размер мал, то можно считать, что напряжения равномерно распределены не только по ширине (на основании третьего допущения и закона равновесия ), но и по длине сечения 1234, следовательно, создают усилие

(а)

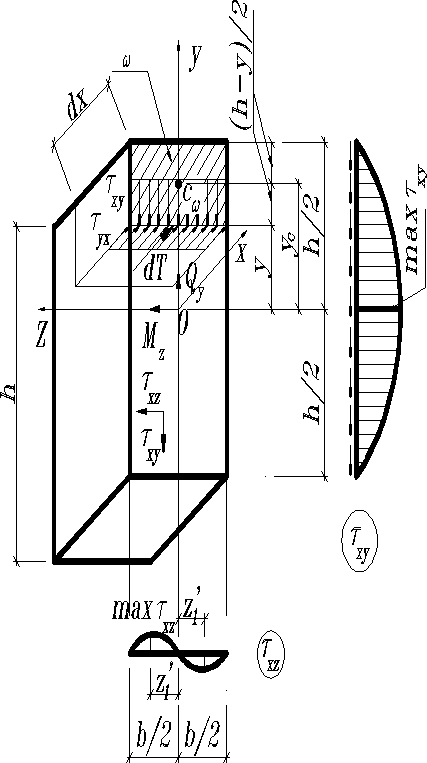
В свою очередь dT определяется выражением (1), которое с учетом (2) принимает вид

(б)

где -статический момент относительно главной центральной оси инерции z части поперечного сечения площадью w (на рис.3 –заштрихована), расположенной выше точки вблизи которой определяется .

Приравнивая правые части уравнений (а) и (б) и деля полученное равенство на , получим

Сечение постоянно по длине балки, т.е. не зависят от Х, а , поэтому .

Согласно, закона равновесия касательных сил, равномерно распределенные (см. третье допущение) касательные напряжения возникают в поперечных сечениях расположенных вблизи линии 12 и равные

(3)

Знаком минус учтено направление , которое всегда противоположно направлению вектора поперечной силы . Формула (3) впервые была получена Д.И.Журавским в 1855 году и носит его имя. Закон распределения по сечению напряжений при и заданной силе определяется изменением статического момента

Подставляя в (3) значения и после преобразований найдем, что

(4)

Выражение (4) является уравнением параболы, следовательно, касательные напряжения по высоте балки прямоугольного поперечного сечения изменяются по параболическому закону. Экстремальные имеют место вблизи точек, расположенных на оси Z () ; ;

т.е. в 1,5 раза больше напряжения, полученного в предположении о равномерном распределении по высоте сечения.

В таблице приводятся численные коэффициенты, на которые умножить приближенные значение , чтобы получить компоненту полного напряжения и при точном расчете, выполненном методом теории упругости для балки из материала с коэффициентом Пуассона

Координаты точек	Напряжение	h/b
		5	2	1	0,5
y=0, z=0		0.9998	0.083	0.940	0.856
		0	0	0	0
y=0,		1.0004	1.003	1.126	1.396
		0	0	0	0
		0	0	0	0
		0.0101	0.040	0.114	0.310

Видим, что:

элементарная формула (3) дает практически точные когда ;
наибольшие напряжения имеют место вблизи точек с координатами на верхней и нижней гранях (эпюру ), но вдоль осей y и z и при , .

В инженерных расчетах пользуются формулой (3) и в случаях , а компонентой обычно пренебрегают.

Двутавровое поперечное сечение

Двутавр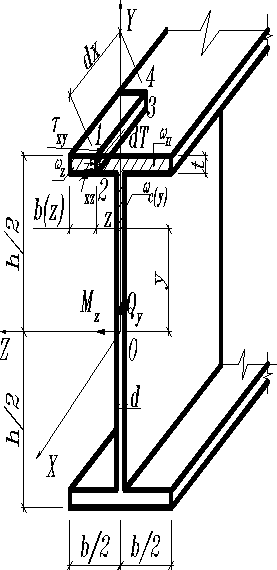

рассматривают как сечение, составленное из трех прямоугольников: двух полок высотой t шириной b и стенки высотой и шириной d. Пусть и в несколько раз больше t и d. Тогда с достаточной точностью можно принять, что в стенке касательные напряжения представлены только составляющими равномерно распределенными по ширине d, а и вычислять по формуле (3). Статический момент относительно главной центральной оси инерции z части поперечного сечения площадью лежащей выше точки с ординатой определяется выражением

(5)

где h – высота двутавра; -статический момент полки с площадью относительно оси z, ординат центра тяжести, которой равна ;

-статический момент стенки с площадью относительно оси z, имеющий ординаты центра тяжести .

Теперь

(6)

Следовательно, напряжение по высоте стенки изменяется по параболическому закону и направлена противоположно вектору.

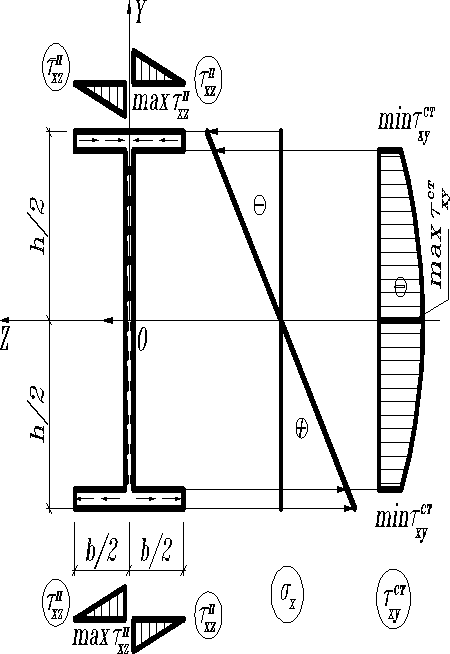
Напряжения в стенке

В полке уже нельзя полагать напряжения равномерно распределенными по ширине b. В свесах полок , то вертикальной составляющей полного напряжения на этих участках пренебрегают и эпюру по высоте полки не строят. Здесь более существенным компонентом является , для отыскания которого, например, в левой верхней части полки, на расстояние z мысленно проводим вертикальное сечение , и выполнив операции аналогичные использованным при выводе формул (3) находим . А так как, , то в интервале и получим

(7)

Т.о. по длине свесов полок напряжение распределяются по линейному закону. При положительной поперечной силе будем иметь:

; ;

В полках направлены либо к оси y, либо от неё, в стенке - против направления . Горизонтальные напряжения образуют систему самоуравновещивающихся сил. Поперечная сила в основном воспринимается стенкой, поэтому в несколько раз больше , разница между и менее существенна. На полки, расположенные в зонах действия наибольших нормальных напряжений приходится значительная доля изгибающего момента . Например для стандартного двутаврового профиля №24равнодействующая равна , , изгибающий момент, воспринимаемых полками равна , . Таким образом, двутавр является одним из рациональных типов сечений в случае поперечного плоского изгиба.

В действительности и будут иными- влияет резкое изменение сечения при переходе из полки к стенке, вызывающие увеличение напряжений. Для устранения этого явления в вершинах входящих углов устраивают закругления (галтели). Вообще, распределение касательных напряжений в областях соединения полок со стенкой следует сложному закону.

Сплошное круглое поперечное сечение

Исследуем касательные напряжения вблизи точек хорды AB находящейся на расстоянии y от центральной оси инерции z, если в сечении , .

Оставляя в силе допущение о равенстве вертикальной составляющей полного напряжения вблизи всех точек с ординатой можно определить эту составляющую по формуле (3)

(8)

где -ширина сечения на уровне y (длина хорды AB);

-статический момент кругового сегмента относительно оси z, расположенного выше прямой AB и имеющего площадь ; и -центральный момент инерции и площадь круглого сплошного поперечного сечения радиусом .

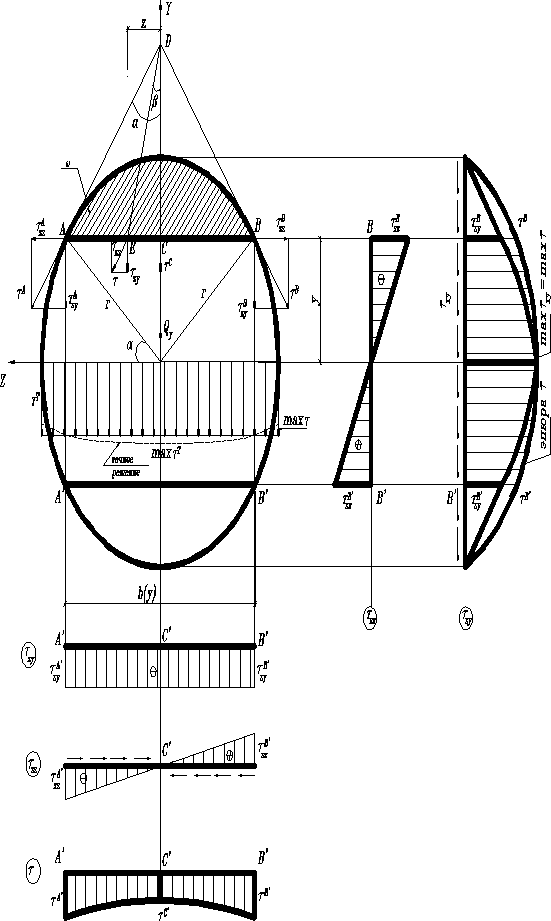
Напряжения у точек контура A и B направлены по касательным к окружности контура. В силу симметрии, напряжения вблизи средней точки С хорды AB параллельно оси y. Линия действия пересекутся в точке D на оси y. Имея в виду полную симметрию круга, примем гипотезу, сто направления всех полных касательных напряжений у горизонтальной прямой AB сходятся в этой точке D. Тогда (знаком минус учтено направление , но

поэтому

(9)

(10)

Эпюра имеет параболическое очертание с наибольшим модулем при y=0.

Компонента вдоль горизонтальной () и вертикальной () хорд изменяется по линейному закону, экстремальное значение имеет место вблизи точек контура с координатами , а по осям y и z . Полное касательное напряжение является нелинейной функцией y и z, у точек, расположенных на горизонтальном диаметре . Результаты изложенной приближенной теории, хорошо согласуется с точными .

Рассмотренные примеры позволяют сделать некоторые общие заключения о касательных напряжениях в сечениях при плоском поперечном изгибе:

вид эпюры зависит от формы поперечного сечения балки;
формула Журавского вносит погрешность, которая не очень существенно сказывается на результатах расчетов при изгибе балок сплошных сечений высотой h порядка ширины b ;
в тонкостенных элементах с большой степенью точности можно считать, что полное касательное напряжение направлено параллельно касательной к срединной линии и распределяется равномерно по толщине контура;
под действием поперечное сечение балок искривляется.

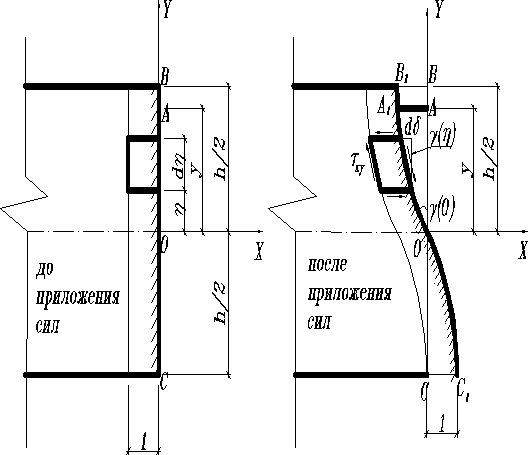
Поясним последнее. Для элемента высотой и длиной 1, находящейся на расстоянии от продольной оси, например балки, прямоугольного поперечного сечения с имеем

Интегрируя полученное выражение, находим абсолютный сдвиг на уровне y вызванный

Из графика функции представленного на рисунке видно, что поперечное сечение балки не остается плоским.

Напряжения при плоском поперечном изгибе