Основные задачи сопротивления материалов

Лекция №1

1. Основные задачи сопротивления материалов

Сопротивление материалов – инженерная наука, в которой решается задача о выборе материала и назначение размеров любого элемента конструкции при обеспечении долговечности и экономичности конструкции в целом. Запроектированное тело должно надежно сопротивляться внешним воздействиям. Элемент конструкции считается прочным, если под действием внешних факторов он не разрушается, жестким - если изменение геометрических размеров его вследствие деформации не превышают заданных значений, и устойчивым, если сохраняется первоначальная форма равновесия его.

Остановимся пока на рассмотрении вопроса обеспечения прочности материала.

Основным объектом исследования в сопротивление материалов является брус (стержень). Брус- материальное тело, одно из измерений которого (длина L) значительно больше двух других. Также в сопр. мат. исследуются пластины (плита)-(это твердое тело, ограниченное двумя плоскими поверхностями, расстояние между которыми () значительно меньше двух других измерений ширины и длины ) и оболочки (материальное тело, ограниченное двумя криволинейными поверхностями, расположенными на близком расстоянии друг от друга. Толщина оболочек значительно меньше двух других измерений, т.е. ширины и длины. ). Массивные тела ( когда все три размеры - величины одного порядка) изучаются в механике деформируемого тела на более строгих, чем в сопротивление материалов, математических началах.

{Брус может быть образован перемещением плоской фигуры (W) вдоль прямой или кривой линии (L). Плоская фигура при этом перпендикулярна касательной в точке (O) к линии (L). Если линия (L) геометрическое место центров тяжестей площади (А) фигуры (W), то оно называется осью бруса. Фигура (W) называется поперечным сечением бруса. Если фигура (W) меняет свои размеры по мере продвижения по линии (L), то брус называется брусом переменного сечения. Валы, оси, балки, крюки т.д. являются примерами бруса.)

(Характеристики материалов и основные гипотезы об их свойствах.

Внешние силы вызывают деформацию тела, т.е. изменение их размеров или формы, либо то и другое одновременно. Различают общую деформацию, распространяющуюся на весь объём тела, местную деформацию, происходящую лишь в малой части объема тела. Эти деформации могут быть:

• упругими (обратимыми) – тело после снятия нагрузки восстанавливает форму и размеры;
• остаточными (необратимыми) – не исчезающими после снятия нагрузки.

Если остаточная деформация не сопровождается местным разрушением, то она называется пластической. Если же при малых остаточных деформациях происходит разрывы, то деформация называется хрупким. Деформации, зависящие от времени называются вязкими. К проявлению вязких свойств материала относится ползучесть (рост деформации при постоянной нагрузки) и релаксация (уменьшение внутренних усилий при постоянной полной величине деформации).)

В сопр.мат. принимаются некоторые упрощающие допущения относительно свойств материалов. Считается, что материал тела: 1) имеет сплошное (непрерывное) строение; 2)однороден, т.е. обладает во всех точках одинаковыми свойствами; 3) изотропен, т.е. имеет во всех направлениях одинаковые свойства. Таким образом в сопр.мат. рассматривают материалы как однородную изотропную сплошную среду независимо от микроструктуры. Свойства такой среды, называемой расчетной моделью твердого тела, определятся расчетными характеристиками, являющимися некоторыми средними величинами, полученными в опытах с образцами из соответствующих материалов.

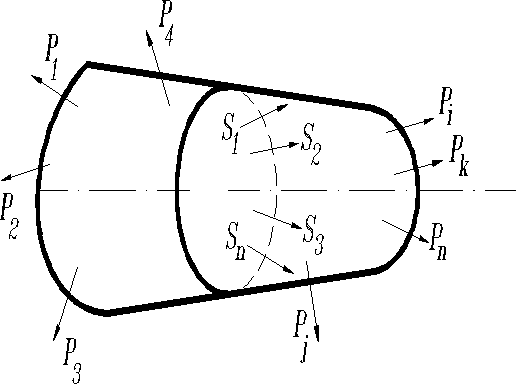
Пусть реальное твердое тело находится в равновесии под действием внешних сил . При этом между частицами тела возникают силы взаимодействия - внутренние усилия (силы). Они стремятся сохранить тело, как единое целое, препятствуя деформации его, а внешние силы наоборот.

При некотором увеличении сил пропорционально одному и тому же параметру, то уравнения равновесия нарушатся. Но возникающие при этом внутренние усилия могут оказаться недостаточным для сохранения тела как единого целого, и оно может разъединиться на части – разрушиться.

Условие разрушение ;

Условие прочности ;

где -действующее внутреннее усилие; -разрушающее внутреннее усилие.

Так как конструкция должна иметь определенную гарантию против разрушения, то условие прочности целесообразно представить в виде , где -допускаемое усилие материала; -коэффициент запаса прочности материала против разрушения.

Классификация внешних сил

Внешние силы воздействия на твердое тело есть результат взаимодействия с другими телами, среди которых могут быть твердые тела, жидкие и газообразные среды. Это взаимодействие происходить на границе тела – его поверхности – при непосредственном механическом взаимодействии (поверхностные силы) или может быть распределен по объему тела, если взаимодействие носит гравитационный (инерционный) или электромагнитный характер.

Поверхностные силы – приложены по всей или некоторой части поверхности тела. Если размеры площади приложения сил малы по сравнению с размерами тела, то размерами названной площади пренебрегают и представляют нагрузку в виде силы Р или пары сил М, приложенной в точке элемента. Такую нагрузку называют сосредоточенной и выражают,, например, в Ньютонах для силы или Ньютон на метр для пары сил.

Если силы приложены по всей или значительной части поверхности тела, то их называют распределенными. Они выражаются в единицах силы отнесенных к длине q (н/м) или площади p н/м2. Давление колеса на рельс можно представить сосредоточенной силой, собственный вес снегового покрова, приходящейся на единицу длины кровельной балки - распределенной нагрузкой q, а давление газа на стенки котла - распределенной нагрузкой p.

Объемные силы (силы тяжести тела, силы инерции, магнитные силы и т.д.) приложенные к любой части объема тела, характеризуется силой, отнесенной к единице объема (н/м3), или к единице длины q (н/м - погонный вес).

Помимо активных (первичных) сил к внешним силам относятся и реактивные (вторичные) силы – реакции связей, дополняющие систему сил до равновесия. Вся система активных и реактивных сил называется нагрузкой.

По характеру действия различают статические и динамические нагрузки. Статические – изменяют величину и направление с очень небольшой скоростью, так что возникающие при этом ускорениями тел и его частей можно пренебречь. Динамические нагрузки сопровождаются интенсивными во времени ростом нагрузок, вызывающих возникновение значительных ускорений, в результате чего появляется необходимость учитывать силы инерции (ударные нагрузки, повторно-переменные, внезапно приложенные и т.д.).

По времени действия различают постоянные (собственный вес конструкции) и временные (машины, люди, ветер, снег и т.д.) нагрузки. Перечисленные постоянные и временные нагрузки являются полезными или регулярными. Могут быть случайные нагрузки (например, сейсмические).

2.Метод сечений.

Для нахождения внутренних сил в сопр.мат. применяется метод сечений.

При этом нагруженное произвольной уравновешенной системой сил тело в интересующем месте мысленно рассекается плоскостью “m-m” на две части В и С, и, например часть В рассматривается отдельно. Действие части С на В заменим системой внутренних сил . Часть В находится в равновесии под действием внешних сил (P) и внутренних (S) сил. Пусть - главные вектор и момент внешних сил, приведенных к точке О сечения. Тогда условие равновесия отделенной части тела имеет вид

и или .

Т.е. главный вектор и момент внутренних сил должны быть равны по модулю соответственно внешних сил, но иметь противоположные направления. Так можно найти главные вектор и момент внутренних сил. Заметим, что при действии произвольной системы внешних сил в различных сечениях возникают различные внешние силы.

3.Понятия о напряжениях и напряженных состояниях.

Внутренние усилия характеризуются интенсивностью, т.е. силой отнесенной к единице площади. Эта интенсивность называется напряжением и измеряется в паскалях (Па=н/м2). Определим напряжение.

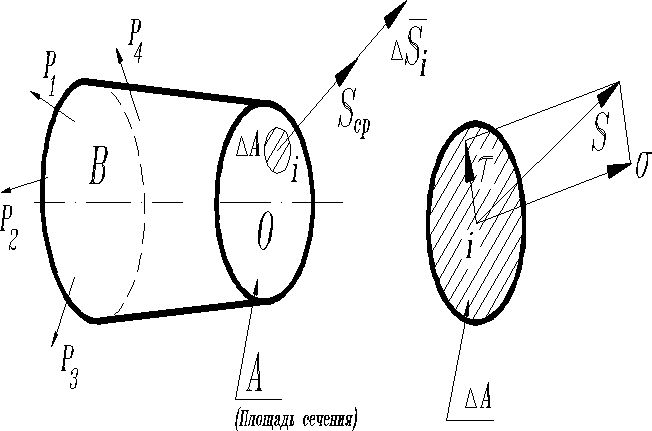
Для этого в границах сечения А вблизи точки выделим бесконечно малую область площадью . Равнодействующую внутренних сил действующих в границах обозначим . Тогда величина - средняя интенсивность внутренних усилий на площадке или среднее напряжение в указанной области. Истинное полное напряжение вблизи точки получим из выражения . Напряжение не зависит от размеров сечения и может служить количественным показателем, позволяющим судить о прочности материала вблизи заданной точки.

Полное напряжение представляет вектор и обычно раскладывается на составляющие. Составляющая полного напряжения на нормаль к сечению обозначается буквой и называется нормальным напряжением. Составляющим полного напряжения в плоскости сечения называется касательным напряжением и обозначается буквой .

Совокупность напряжений, возникающих во множество сечений, проходящих через произвольную точку тела, образует напряженное состояние вблизи этой точки. Если в любом сечений тела все составляющие полного напряжения распределяются равномерно по сечению, то такое напряженное состояние называется однородным. Во всех других случаях напряженное состояние будет неоднородным.

Перемещения, деформация и деформированное состояние.

Под действием внешних сил точки тела занимают новые положения – перемещаются. Проекцию полного перемещения на ось Х будем обозначать буквой , тоже на оси Y и Z – соответственно буквами .

Так различные точки тела получают различные перемещения, то происходит изменение размеров тела и формы, либо то и другое одновременно. Тело деформируется. Изменение линейных размеров тела и его частей называется линейной, а изменение угловых размеров – угловой деформацией. Совокупность линейных и угловых деформаций по различным направлениям и плоскостям, проходящим через точку, образует деформированные состояния вблизи этой точки.

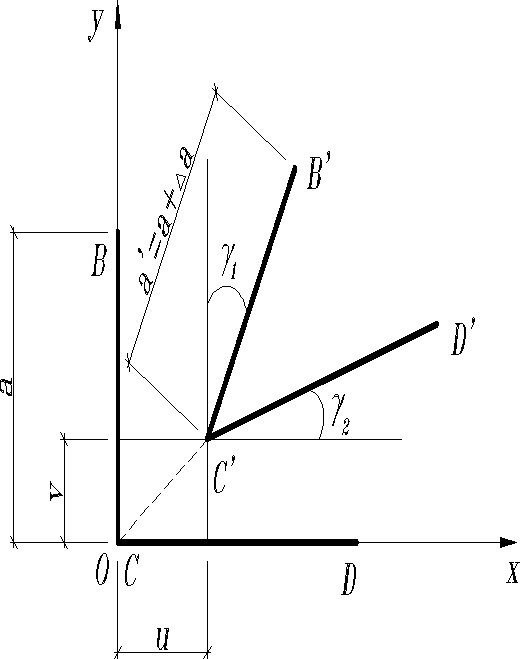
Если вблизи исследуемой точки выделить бесконечно малый прямоугольный элемент ВСD, то в результате деформирования тела он в общем случае займет новое положение . В виду малости элемента, его стороны останутся прямолинейными, но длины их изменяются (увеличатся или уменьшаться) и они повернутся по отношению к первоначальному положению. Точка C () займёт новое положение с координатами (). Отрезок есть полное перемещение точки C, проекции этого перемещения на координатные оси .

Длина, например стороны ВC, до приложения сил равная , изменится и станет равной . Полная абсолютная линейная деформация стороны ВC будет . Отношение - называется относительной линейной деформацией и служит мерой степени деформации материала, т.к. не зависит от размеров тела. Деформации по оси Х обозначается , по сям Y и Z - . Угловые или сдвиговые деформации в плоскости XOY , в плоскости XOZ и YOZ - . Положительным линейным деформациям отвечает увеличение размеров тела (удлинения) по соответствующим направлениям. Положительным угловым деформациям соответствует уменьшение углов между положительными направлениями координатных осей, отрицательным – увеличение углов.

Принципы начальных размеров и независимости действия сил.

Определим абсолютную деформацию бруса длиной L=100 см, изготовленного из малоуглеродистой стали, в случае если его относительная деформация стала равной допустимой .

.

Так как деформации основных строительных материалов в системах обычно малы по сравнению с геометрическими размерами тел, то при анализе внутренних сил применяют:

1.Принцип начальных размеров, согласно которого при составлении уравнений равновесия тело рассматривается как недеформированное, имеющее те же геометрические размеры, что и до нагружения внешними силами.

2.Принцип независимости действия сил или принцип суперпозиции, по которому полные перемещения и внутренние усилия, возникающие в упругом теле от различных факторов (несколько сил, температурных воздействий и т.д.) равны сумме перемещений и усилий, вызванных каждым из этих факторов, и не зависит от последовательности их приложения.

Например, в случае действия на стержневую систему силы узел А переместится вниз, заняв положение А1и угол изменится. Но, на основании п.н.р., усилия в стержнях системы определяется из уравнения равновесия узла А (), полагая геометрические размеры системы () неизменными. Эти усилия и перемещения узла А, в соответствии с п.с., можно найти рассмотрев действие на систему сил в отдельности и сложив результаты двух расчетов.

Основные задачи сопротивления материалов