Определение перемещений при плоском поперечном изгибе
Определение перемещений при плоском поперечном изгибе.
Рассматриваются балки, представляющие собою прямых стержней с постоянным по длине поперечным сечением и продольной плоскостью симметрии. Под действием вертикально направленных внешних сил расположенных в плоскости симметрии, балка изгибается.
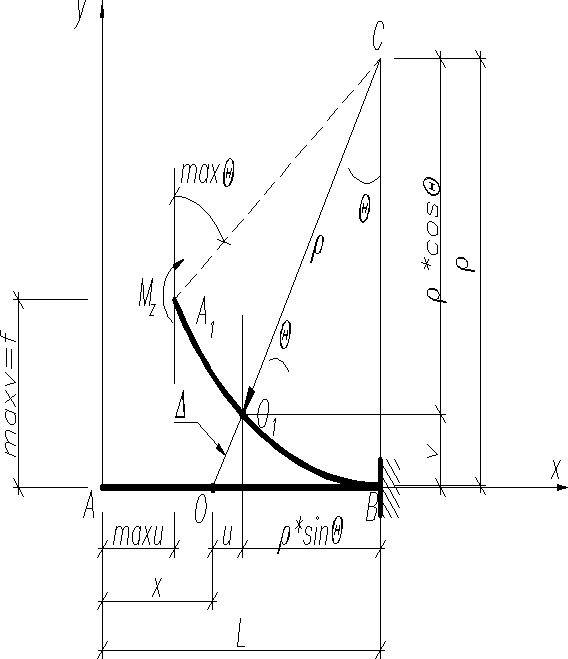
В дальнейшем предполагается, что пластические деформации при этом не возникают. Продольная ось балки АОВ превращается в некоторую кривую А1О1В1, которая называется изогнутой осью (линией погиба, упругой линией). Поперечное сечение занимает новое положение (), поворачивается на угол (угол поворота сечения) по своему первоначальному положению () и получают линейные перемещения . Проекции полных перемещений центров тяжести (О) поперечных сечений обозначаются :
- на продольную ось недеформированной балки ;
- на нормаль к продольной оси недеформированной балки v – компонента называется прогибом балки в данном сечении.
Угловые и линейные перемещения от действия на элемент нормативных нагрузок не должны превышать установленных пределов. Обычно максимальный прогиб (стрела прогиба) ограничивается определенной величиной – допускаемым прогибом , составляющим (от длины пролета) в зависимости от назначения сооружения или машины. Получающие при этом углы поворота сечений не превышают 10. Поэтому для осуществления расчета на жесткость необходимо научится вычислять перемещения балки от любой внешней нагрузки. При этом необходимо:
- располагать начало координат на одном из концов балки, направляя ось Х по продольной оси недеформированного элемента, а ось Y –вверх;
- расчет производим от действия нормативных нагрузок.
Перемещения при чистом плоском изгибе ()
Мысленно рассечем незагруженный брус двумя сечения I-I и II-II на расстоянии равным 1, малым по сравнению с поперечными размерами. Выделим на расстоянии от нейтральной линии (оси Z) отрезок gh. Относительная деформация этого отрезка под действием внешних сил определяется по закону Гука или с учетом найдем
(1).
Значит, деформации по высоте поперечного сечения распределяются по линейному закону. При - верхняя часть бруса () укорачивается, нижняя ()-удлиняется. Отрезки, расположенные на нейтральном слое, не изменяют свою длину .
Сечения занимают положения . Касательных напряжений, по условию задачи, в поперечных сечениях нет. Поэтому сечения -нормальные к продольном линиям до деформации, заняв положение , останутся нормальными к линиям и после деформирования бруса (например, угол ) будет возможным, если продольные линии изогнуться по дуге, а следовательно, и весь брус изогнется, При деформации материала поперечное сечение поворачивается относительно нейтральных линии как твердое тело, оставаясь плоским.
Продолжим линии до взаимного пересечения в точке О, которая является центром кривизны изогнутого бруса. Обозначим буквой -радиус кривизны оси бруса в деформированном состоянии и поставим задачу определить кривизну .
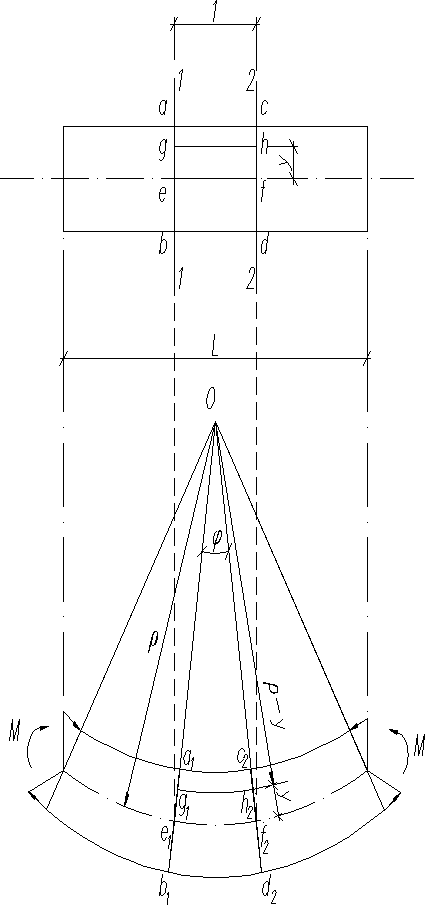
Свяжем функциональной зависимостью кривизну с внешними силами, представленными изгибающим моментом . Из геометрических соображений имеем:
.
Находим абсолютную деформацию отрезка gh
а затем и его относительную деформацию
(2)
Т.к. левые части уравнений (1) и (2) равны, то, приравняв правые части, получим формулу для определения кривизны оси изогнутого бруса
или (3)
При постоянных значениях изгибающего момента , и изгибной жесткости величина . Следовательно, продольная ось однородного призматического бруса под действием приложенных к его торцам пар искривляется (изгибается) по дуге круга радиусом .
Изучаемый вид напряженного состояния называется плоским изгибом, потому, что поперечные сечения бруса и после деформации остаются плоскими, а продольные слои изгибаются (искривляются) по дугам. При этом как будет показано в дальнейшем, ось изогнутого бруса располагается в плоскости действия внешних сил или в параллельной ей плоскости.
Был рассмотрен плоский изгиб при . Если проделать подобные исследования, положив то получим
(4); (5); (6).
Таким образом, может быть два случая плоского изгиба, в плоскости XCY -, XCZ-.
Признак плоского изгиба:
- нейтральная линия сливается с вектором изгибающего момента;
- ось изогнутого бруса располагается в плоскости действия внешних сил или параллельной ей плоскости.
Условие плоского изгиба:
- изгиб будет плоским, если плоскость действия внешних сил перпендикулярна к одной из главных центральных осей инерции поперечного сечения бруса.
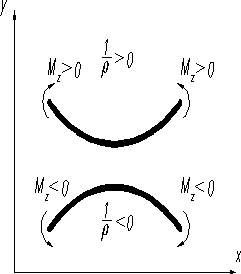
Под действием пары сил с моментом –Mz, например, на консоль линия прогибов А1О1В1 изгибается по дуге окружности, длина которой останется равной L, а кривизна определяется выражением . Если , то ось изогнутой балки обращена вогнутостью вверх и , при получается . Имеет соответствие между знаками изгибающего момента и кривизны.
Угол поворота и прогиб , и перемещение сечения, расположенного на расстоянии x от левого конца балки соответственно равны
Наибольшие получим при х=0.
; ; .
При достаточно большом угле поворота сечения {}, для инженерной практике, будем иметь
.
Т.к. значительно меньше , то в обычных балках компонентом пренебрегают, определяя только угол поворота сечений и прогибы .
Перемещения консоли от сосредоточенной силы на свободном конце
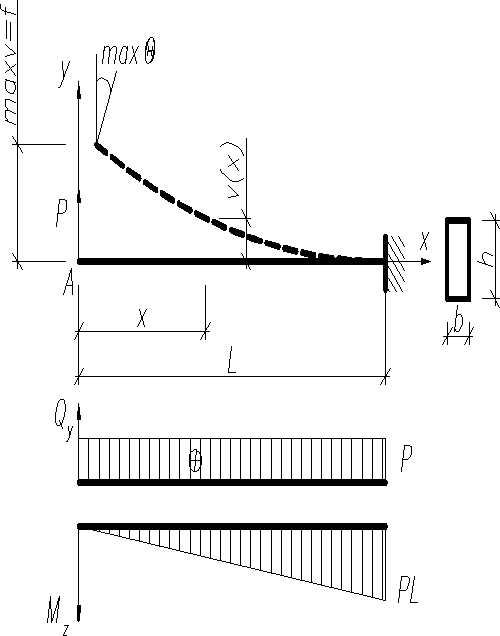
Исследуем перемещение балки прямоугольного поперечного сечения , схема и эпюры которой представлены на рис. . Составляющие внешних сил в произвольном сечении представлены поперечной силой и изгибающим моментом . Применяя принцип суперпозиции, определим и отдельно от Qy и Mz.
Влияние поперечной силы на перемещение балки
Наибольшие касательные напряжения возникают во всех сечениях вблизи точек с координатами y=0 и вычисляются по формуле , а нормальные и касательные напряжения здесь равны нулю. Мысленно выделенные у этих точек
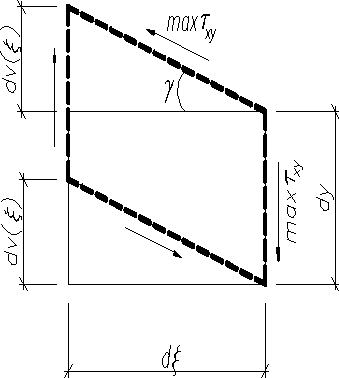
прямоугольные до приложения силы бесконечно малые элементы длиной и высота dy под действием превращаются в параллелограммы и занимают положения, показанные на рис. . штриховыми линиями. Левая грань элемента, находящаяся, например, на расстоянии от свободного конца балки в границах интервала , получит по отношению к первой грани положительное (в направлении оси y) вертикальное перемещение
Тогда полный прогиб центра тяжести сечения с абсциссой x будет равен
(а);
Откуда
При -кривизна плоской линии, определяемая (см.курс высшей математики) выражением
(7)
будет равна нулю. Следовательно, постоянная по длине балки поперечная сила не вызывает искривления продольной оси этой балки.
Заметим, что здесь и в дальнейшем положительными считаются:
- прогиб при перемещении точек вверх, независимо от расположения начала координат;
- тангенс угла поворота- при повороте сечения против часовой стрелки, для случая начала координат на левом конце балки, и по часовой стрелке, когда начало координат на правом конце.
Из уравнения (а) видно, что наибольший прогиб имеет место при х=0
,
а пологая , получим (8).
Влияние изгибающего момента на перемещения балки
Т.к. от действия Qy(x) ось балки остается прямой, то формулой (3) можно воспользоваться и при . Приравнивая правые части выражений (7) и (3) и учитывая, что знаки и кривизны совпадают, получаем точное дифференциальное уравнение оси изогнутой балки
(9)
При прогибах , имеющих место в инженерных конструкциях, величина - оказывается ничтожно малой по сравнению с единицей. Поэтому, отбрасывая в знаменателе формулы (9) будем иметь приближенные уравнения оси изогнутой балки
(10)
которым обычно пользуются для определения перемещения при . В уравнении (10) изгибающий момент вычисляется для недеформированной балки.
Умножив на dx обе части выражения (10) и проинтегрируем
и (11)
Интегрируя второй раз, получим
(12)
здесь C и D- постоянные интегрирования;
С - пропорциональна тангенсу угла поворота сечения в начале координат;
D- пропорциональна прогибу сечения в начале координат.
(11)-уравнение тангенсов углов наклона касательной к изогнутой балки или уравнения тангенсов углов поворота сечений;
(12) -уравнение прогибов изогнутой оси балки.
В рассматриваемом случае при имеем
; ; .
Постоянные интегрирования определим из условий закрепления балки (граничных условий):
- тангенс угла поворота сечения -получим .
- в месте заделки при прогиб - получим ;
На свободном конце при х=0
(13);
(14).
Сложив (14) и (8), получим полный прогиб свободного конца балки от поперечной силы и изгибающего момента
Даже при -ошибка при определении без учета влияния поперечной силы составляет 4% от . Аналогичные выводы можно сделать и в отношении .
На участках действия распределенной нагрузки поперечная сила уже является функцией абсциссы x и вызывает искривление оси балки. Но увеличения от этого наибольшего прогиба, например, в консоли прямоугольного поперечного сечения с отношением не превышает 5%.
Вывод: Если высота балки мала по сравнению с её длиной, то, с приемлемой точностью, можно пренебречь влиянием поперечной силы и пользоваться при определении перемещений только приближенным дифференциальным уравнением оси изогнутой оси (10).
Определение перемещений в балках с несколькими участками нагружения.
Поставим задачу:
- определить наибольший прогиб двухопорной балки постоянного поперечного сечения, нагруженной силой P.
Опорные реакции равны . Начало координат возьмем на опоре A. Балка имеет два участка.
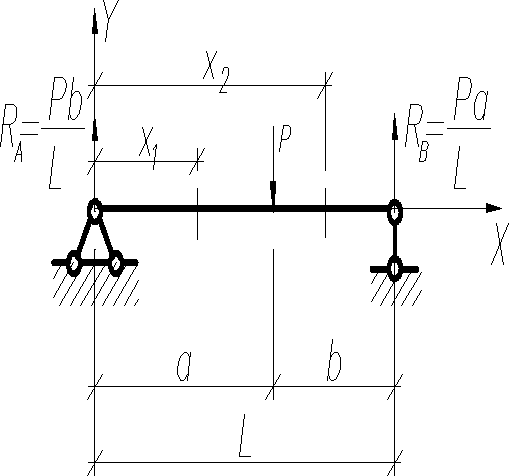
Первый участок
; ; ;
Второй участок
;; .
В решение вошли четыре постоянных интегрирования C1, D1, C2, D2 , т. е. вдвое больше, чем число участков. Если же балка по условиям нагружения имеет n участков, то интегрирования всех дифференциальных уравнений дает 2n постоянных. Для определения этих постоянных можно составить 2n уравнений, используя два условия на опорах и 2(n-1) условий непрерывного и плавного сопряжения изогнутой оси на границе смежных участков, где прогибы и тангенсы углов поворота сечений равны, т.к. нет разрывов и изломов упругой линии. В рассматриваемом случае это:
- в сечении при получим ;
- в сечении при получим ;
- на опоре A при прогиб получим ;
- на опоре B при прогиб получим откуда ;
Пусть . Сечение, в котором прогиб имеет наибольшую величину, определим из условия . Подставляя и в уравнение найдем , тогда
Следовательно
Если сила P находится посредине пролета, то , тогда .
Если отодвигать силу P к правой опоре, то при . Абсцисса с наибольшим прогибом меняется всего от до . Как показывают исследования, разница между прогибом посредине пролета не превышает 3%. Следовательно, . Это заключение применимо при действие на балку любых нагрузок, вызывающих изгиб в одну сторону.
В балках с постоянным поперечным сечением при числе участков этот процесс можно свести к отысканию двух постоянных интегрирования C и D, если соблюдать следующие правила:
- 1) задаваться началом координат общим для всех участков, располагая его в крайней левой (или правой) точке оси балки;
- 2) все составляющие выражения изгибающего момента предыдущего участка сохранять неизменными в выражении изгибающего момента последующего участка (или по другому: правая часть последующего участка должна содержать правую часть предыдущего участка в неизменном виде);
- 3) вновь вводимые в выражение изгибающего момента последующего участка составляющие должны содержать множитель (x-a) где a – сумма длин всех предыдущих участков от начала координат;
- 4) при интегрировании двух членов вида использовать формулу ;
Следствие:
- для выполнения правил 3) необходимо вводить в выражения изгибающего момента сосредоточенный момент с множителем равным единице (здесь -абсцисса сечения, в котором приложен момент );
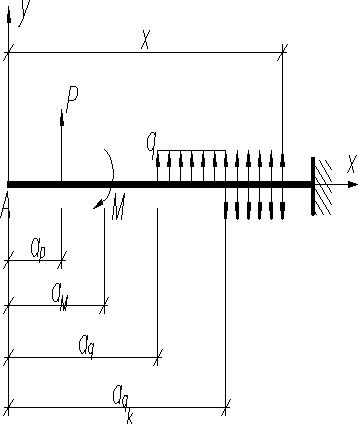
- для выполнения правил 2) нельзя допускать скачка в сторону уменьшения интенсивности распределенной нагрузки. Если по условию задачи произошло, например в сечении с абсциссой , то распределенная нагрузка продолжается до конца балки и добавляется одновременно “компенсирующая” нагрузка обратного знака и той же интенсивностью
Изложенный метод определения перемещений называется методом выравнивания постоянных интегрирования.
Метод начальных параметров
Выбрав начало координат в крайней левой точке оси балки (в точке A на рис. ), составим выражения для изгибающего момента в произвольном сечении последнего 5-го участка с соблюдением выше указанных правил
Тогда дифференциальное уравнение оси изогнутой балки на этом участке примет вид
(а)
Уравнение тангенсов углов поворота
(в)
Уравнение прогибов
(с)
Заметим, что в (а), (в) и (с) в выражения могут быть только положительными величинами. Если , то соответствующая нагрузка расположена справа от рассматриваемого сечения и также, слагаемое должно быть вычеркнуто из выражения. Например, при х=0 из (в) и (с) будем иметь
(d); (e)
-угол поворота и прогиб сечения в начале координат, называемыми начальными параметрами.
Для случая несколько сосредоточенных моментов и сил, а также нескольких участков, распределенной нагрузки формулы (в) и (с) с учетом зависимостей (d)и (e) записываются в следующей форме
(15)
(16)
Выражения (15) и (16) называются универсальными уравнениями тангенсов углов поворота своими знаками все внешние силы (включая опорные реакции), расположенные между началом координат и сечением с абсциссой х, в котором определяются перемещения. Знаки слагаемых определяются знаком соответствующего силового фактора.
Применим уравнении (15) и (16) к нахождению прогиба и угла поворота свободного сечения балки, защемленной одним концом и загруженной равномерно распределенной нагрузкой интенсивностью q (рис. )
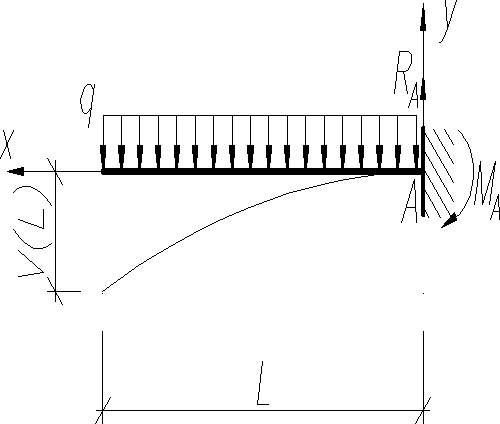
Учитывая, что вместо (15) и (16) получим
Недостаток универсальных уравнений (15) и (16) состоит в том, что их нельзя непосредственно использовать для определения перемещений в балках с переменным по длине поперечным сечением .
Расчет на жесткость при изгибе
Определив значение наибольшего прогиба балки , и сравнив его с допускаемым прогибом , запишем условие жесткости балки
(17)
Например, при известных значениях (см.рис. )
Т.е. жесткость балки обеспечена. Если условие (17) не выполняется, то проводят перерасчет и определяют требуемый момент инерции
Определение перемещений при плоском поперечном изгибе