Внецентренное растяжение и сжатие стержней большой жесткости

Весьма часто равнодействующая внешних сил бывает приложена не в центре тяжести поперечного сечения стержня, а с некоторым смещением (эксцентриситетом) относительно главных центральных осей инерции поперечного сечения, т. внецентренно

Определение напряжений.

Пусть в продольных сечениях напряжения , а в поперечных сечениях нормальные напряжения распределяются по закону (а)

и нет касательных напряжений (в).

Выясним, какими внешними силами создается заданное напряженное состояние.

Решение будем вести относительно главных центральных осей инерции поперечного сечения бруса, для которых

, , (с)

Подставив (а) и (в) в уравнения равновесия и учитывая (с), получаем

(1.1)

(d)

(1.2)

(1.3)

(1.4)

(1.5)

, (е)

(1.6)

, (f)

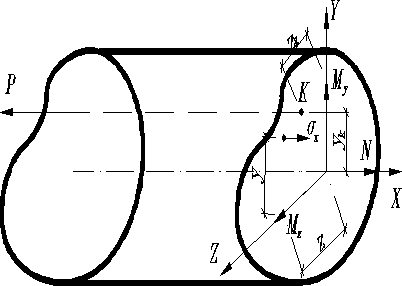
Таким образом, заданный вид напряженного состояния вызывается продольной силой и изгибающими моментами.

Переписав выражения (d), (e), (f) относительно постоянных B, C, D и подставив значения этих постоянных в уравнения (а) получим формулу для определения нормальных напряжений

(1)

-координаты точки, вблизи которой вычисляется нормальное напряжение, относительно главных центральных осей инерции поперечного сечения бруса;

- площадь и главные центральные моменты инерции сечения, соответственно.

Систему представленную продольной силой и парами сил , векторы которых взаимно перпендикулярны, можно заменить одной силой, параллельной и приложенной в точке с координатами . Действительно, пусть на торцах бруса внешние силы приводятся к растягивающей силе Р, параллельной к оси Х. Тогда для левой отделенной части бруса, представленные на рисунке, главные вектор и момент внешних сил в поперечных сечениях будут представлены составляющими

(g); ;

(h); (i).

Здесь знаком минус учтено, то, что направление силы Р и оси Х противоположно (см(д)), и то, что направление момента силы Р относительно оси Z противоположно движению часовой стрелки (см(i)).

Принимая во внимание (g), (h), (i), формулу (1) можно привести к виду

; (2)

-равнодействующая внешних сил (при растяжении вводится в (2) со знаком плюс, при сжатии со знаком минус);

- координаты точки называемой центром растяжении (или давления- в случае сжимающей силы) относительно главных центральных осей инерции поперечного сечения бруса.

Рассмотренный случай напряженного состояния, когда внешние силы приложенные по торцам бруса, приводятся к равнодействующей силе Р параллельной оси бруса, и нормальные напряжения в поперечных сечениях распределяются по закону (1) или (2), называется чистым внецентренным растяжением (или сжатием).

Условие чистого внецентренного растяжения: внешние силы по торцам бруса распределены по закону (1) или (2).

Признак: внешние силы приводятся к равнодействующей силе, параллельной продольной оси бруса.

Если закон распределения внешних сил произвольный, то они приводятся к равнодействующей, параллельной продольной оси бруса, то в сечениях достаточно удаленных от торцов по принципу Сен-Венана напряжения можно определят по формулам (1) и (2).

Понятие о нейтральной линии. Расчет прочности при внецентренном растяжении (сжатии). Эпюра напряжений.

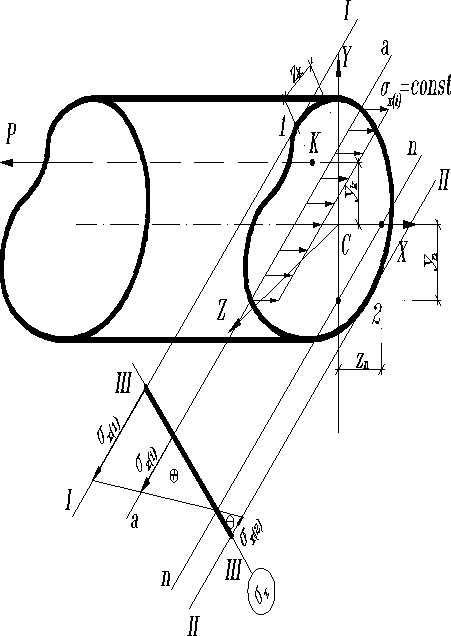
Исследуем распределение нормальных напряжений при внецентренном растяжении бруса с . Из выражения (2) следует, что вдоль любой прямой напряжения распределяется по линейному закону (зависит от в первой степени). Есть также прямые, называемые в дальнейшем изонапряжениями, вблизи которых

и предварительно умножив обе части этой формулы на

или и окончательно

(3) или

где и - квадраты главных радиусов инерции;

-аналог напряжений, возникающего при центральном растяжении (сжатии);

-свободный член.

Выражение (3) представляет собой уравнение прямой в отрезках. Т.к. для различных значений зависимости (3) будут отличаться только свободным членом

, то, следовательно, прямые равных напряжений параллельны между собой . Отрезки , отсекаемые изонапряжениями (3) на главных центральных осях находим из условий

(4)

Изонапряжению на рисунке соответствует прямая а-а.

При определенных значениях нормальные напряжения в поперечных сечениях внецентренно растянутого бруса могут быть не только растягивающими, но и сжимающими, и равными нулю. Точки поперечного сечения, вблизи которых образуют линию, называемой нейтральной. Задавшись , получим и тогда зависимости (3) и (4) примут вид

(5)

; (6)

Выражением (5) представлен уравнение нейтральной линии, а из (6) определяются отрезки , отсекаемые этой линией на координатных осях.

Чем дальше точки сечения располагаются от нейтральной линии, тем больше возникающие вблизи них напряжения . Наибольшие действуют вблизи точек 1 и 2, наиболее удаленных от нейтральной линии. Эти точки найдем, проводя к контуру поперечного сечения бруса касательные I-I и II-II параллельные n-n. Для рассматриваемого случая внецентренного растяжения вблизи точки 1 возникает наибольшее растягивающее напряжение, в вблизи точки 2 наибольшее сжимающее напряжение. Поэтому для обеспечения прочности бруса потребуется выполнение следующих условий

(7)

Эти же условия используются для определения допускаемой силы

(8)

Для наглядного представления напряженного состояния внецентренно загруженного бруса обычно строится эпюра нормальных напряжений в скалярной форме. Для этого в произвольном месте (расстоянии от сечения) перпендикулярно нейтральной линии n-n проводится прямая III-III. Из точек пересечения её с касательными к контуру I-I и II-II откладываются отрезки в определенном масштабе соответствующие и . Отрезки отложены в разные стороны, т.к. , . После чего проводится прямая 1-2, которая если расчет и построения выполнены без ошибок, пересечет линию Ш-Ш и n-n в общей точке О. Образованная фигура называется эпюрой напряжений .

Особенности взаимного расположения центра растяжения (давления) и нейтральной линии

Из выражения (6) следует, что центр растяжения (давления) и нейтральная линия всегда располагаются в противоположных квадратах (знаки и противоположные);

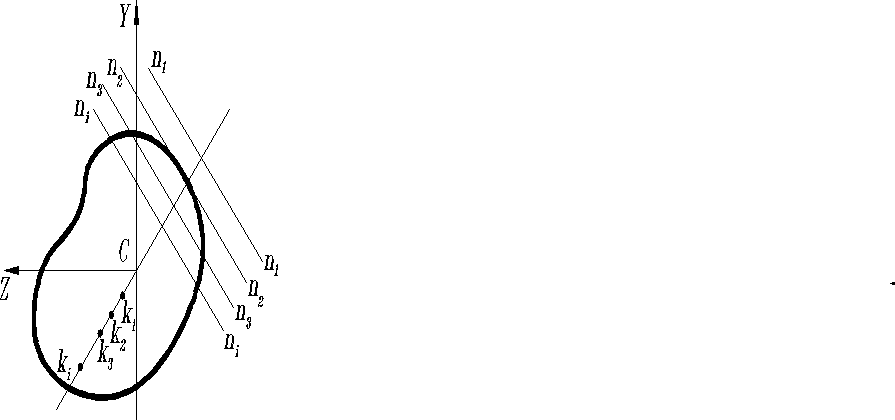
Если , то ; если то и наоборот. При приближении центра растяжения (давления) к центру тяжести поперечного сечения бруса - нейтральная линия удаляется от начала координат и наоборот;

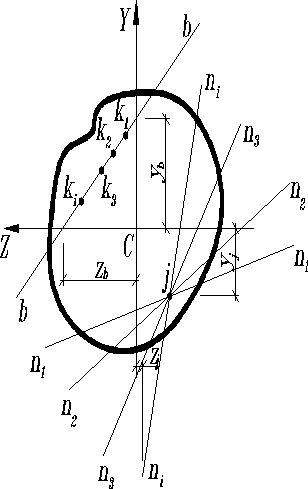
Если центр растяжения (давления) перемещается по прямой b-b, то нейтральная линия поворачивается относительно точки , называемой полюсом. Координаты полюса определяются по формулам

; ; (9)

где -отрезки, отсекаемые прямой b-b на координатных осях.

Два частных случая:

Если центр растяжения (давления) перемещается по центральной прямой, то нейтральная линия перемещается поступательно;

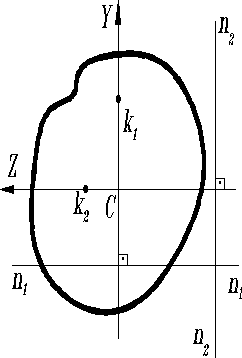
Если центр растяжения (давления) расположен на одной из главных центральных осей инерции поперечного сечения бруса, то нейтральная линия располагается перпендикулярно этой оси.

Ядро сечения. Свойства и способы построения ядра сечения.

При достаточно близком расположении центров растяжении (давления) от центра тяжести центра тяжести бруса нейтральные линии находятся за пределами или касаются сечения. Напряжения вблизи этих точек имеют одинаковый знак, за исключением в точке касания нейтральной линии где . При достаточном удалении центров растяжения (давления) от центра тяжести сечения нейтральные линии пересекают поперечное сечение, возникают растягивающие и сжимающие напряжения.

Материалы, плохо сопротивляющиеся растяжению (бетон, кирпичная кладка, природные камеи, чугун), или совсем не воспринимающие растягивающих усилий (некоторые пластмассы при длительном действии нагрузки), применяются для изготовления элементов подвергающихся сжатию. Представляет интерес установить область таких удалений центров давления от центра тяжести сечения, при которых вблизи всех точек поперечного сечения напряжения будут сжимающими, или, в крайнем случае, равными нулю. Такую область называют ядром сечения.

Если центр давления, расположен на контуре ядра сечения, то нейтральная линия касается контуру поперечного сечения бруса.

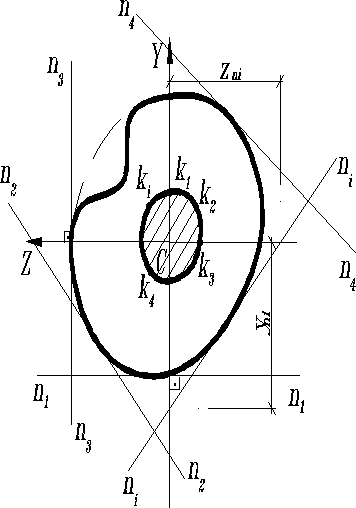
Проводят множество нейтральных линий, касательных к контуру поперечного сечения. Определяя отрезки , отсекаемые нейтральными линиями на координатных осях, по формулам (6) () можно определить координаты соответствующих центров давления. Множество точек, полученных таким образом, образуют замкнутую линию. Часть сечения, заключенная внутри и на самой линии - есть ядро сечения.

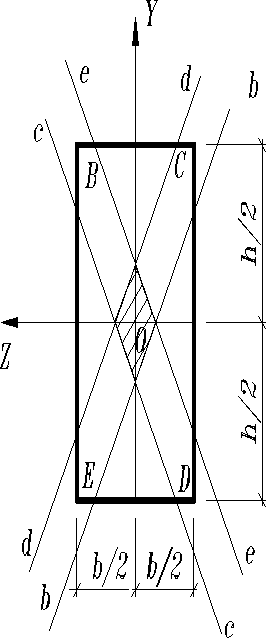
Построим ядро для прямоугольного поперечного сечения. Поворачиваем нейтральную линию n-n вокруг угловой точки сечения В (полюс) с координатами , , тогда отрезки, отсекаемые прямой а-а, по которой перемещаются центры давления, найдем по формулам (9)

; ;

после чего проведем и саму прямую а-а. Затем аналогичным образом, построим прямые b-b, c-c, d-d, соответствующие вращением нейтральных линии вокруг вершин C, D, E. Образованная пересечением прямых фигура 1234 и есть ядро сечения.

Свойства ядра сечения:

Сколько контур поперечного сечения бруса имеет прямых участков – столько ядро сечения имеет вершин;
Сколько вершин имеет контур поперечного сечения бруса- столько прямых участков имеет контур ядра сечения;
Ядро сечения не имеет входящих углов.

Ядром сечения называется область вокруг центра тяжести сечения, расположение в которой центра давления (растяжения) приводит к возникновению во всем сечении напряжений одного знака.

Вычисление деформации бруса.

Для материала, подчиняющегося закону Гука, относительные деформации вычисляем по формуле . В свою очередь . Поэтому или (а),

где -первоначальная длина бруса;

- абсолютная линейная деформация продольного волокна.

С учетом (2) деформация произвольного продольного волокна при внецентренном загружении бруса будет определяться из выражения

(10)

Найдем деформацию продольной оси, для которой зависимость (10) при , приводится к виду , т.е. тому же, что и в случае центрального загружения бруса.

Вывод: при внецентренном растяжении (сжатии) удлинение (укорочение) продольной оси бруса не зависит от точки приложения равнодействующей внешних сил.

Внецентренное растяжение и сжатие стержней большой жесткости