Динамическая нагрузка

Нагрузка, прикладываемая с большой скоростью и вызывающая ускорения частиц тела или соприкасающихся с телом элементов, называется динамической. Например:

силы инерции в деталях машин, движущихся возвратно- поступательно с переменной скоростью;
нагрузки чрезвычайно малой продолжительностью;
периодически меняющиеся во времени со значительными скоростями напряжения, возникающие во вращающихся осях машин, находящихся под действием постоянной поперечной нагрузки.

Динамические нагружения, по сравнению со статическими существенно изменяют процесс деформирования и поведение материала. Поэтому изучение действия динамических нагрузок ведут в направлении: а) нахождения величины динамических деформаций и напряжений; б) исследования влияния этих напряжений на механические свойства материалов.

Общий метод расчета на динамические воздействия основан на принципе Даламбера:

Всякое движущиеся тело может рассматриваться как находящиеся в состоянии мгновенного равновесия, если к действующим на него внешним силам добавить силу инерции, равную произведению массы тела на ускорение центра тяжести, которая направлена противоположно ускорению.

Тогда, если известны силы инерции, то можно применить метод сечений и для определения внутренних усилий использовать уравнения равновесия. В тех случаях, когда определение сил инерции затруднено (например, при ударе), для нахождения динамических напряжений и деформаций используется закон сохранения энергии.

Равноускоренное движение тела. Динамический коэффициент.

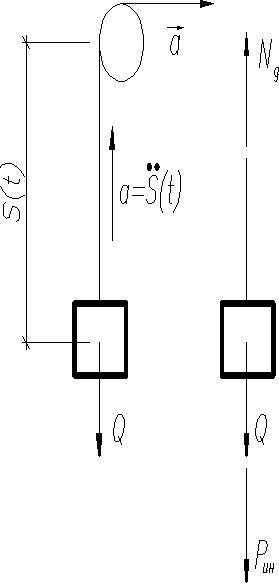
Рассмотрим равноускоренный подъем груза , подвешенный на тросе. К телу кроме его веса по принципу Даламбера должно быть приложена сила инерции , направленная в сторону, противоположную ускорению (ускорение равнопеременного движения). Применяя метод сечений, из условия равновесия определим значения усилия возникающего в тросе при подъёме

или

Выражение в скобках характеризует отличие усилия в торосе при равноускоренном подъёме груза от усилия, возникающего при его статическом приложении. Следовательно

. Здесь - усилие в тросе при статическом нагружении.

Усилие от динамической нагрузки равно усилию от статической нагрузки, умноженному на динамический коэффициент. Для определения численного значения усилия в тросе необходимо найти ускорение . Воспользуемся уравнением равнопеременного движения при нулевой начальной скорости

, где - расстояние, пройденное за время .

Влияние центробежных сил

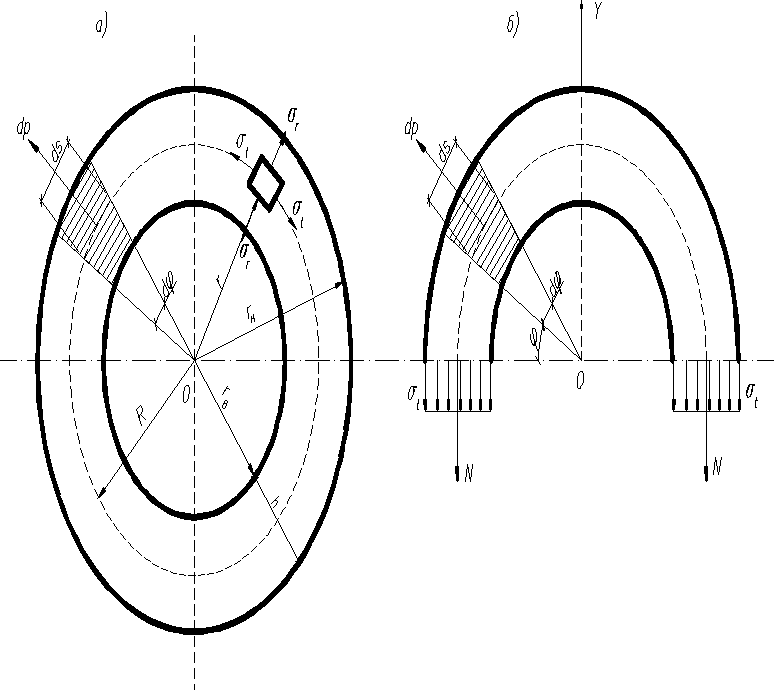
При вращении тела с постоянной угловой скоростью , угловое ускорение равно нулю. Поэтому тангенциальное ускорение , а радиальное (центростремительное) направленное к центру вращения ускорение , где - радиус – вектор точки. Следовательно, к любому элементарному объему вращающегося тела с массой приложена сила инерции (центробежная сила), направленная в сторону, противоположную , и равная . В результате чего в теле возникают напряжения. В случае вращения тонкого кольца вокруг оси О с радиус R срединной линии которого значительно больше высоты сечения, что делает возможным пренебречь сопротивлением кольца изгибу.

На элемент кольца длиной действует центробежная сила .

Здесь - площадь поперечного сечения кольца; - толщина кольца ; - объемный вес материала; -ускорение свободного падения.

В кольце возникают растягивающие усилия N. Разрежем кольцо по диаметру и спроектируем все силы на ось :

или . Откуда

или и .

Полагая напряжения распределенными равномерно по сечению, будем иметь

(1)

Т.о., напряжения в кольце зависят от объемного веса материала и линейной скорости . Полученное приближенное решение в качестве первого приближения может быть использовано при расчете обода маховика и других аналогичных элементов, где допустимо пренебречь влиянием спиц.

Определение перемещений и напряжений при ударе

Удар – взаимодействие движущихся тел в результате их соприкосновения, связанное с резким изменением скоростей точек этих тел за весьма малый промежуток времени.

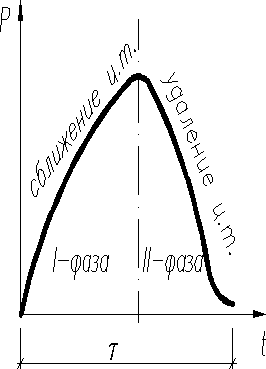
Импульс силы удара равен изменению количества движения и может быть найден достаточно точно, а вот силу удара и его продолжительность до сих пор определить не удается. Это объясняется тем, что за исключительно короткий промежуток времени, в который совершается удар, трудно произвести измерения, связанные с определением силы удара. Поэтому производят условный расчет на удар, по которому определяют внутренние силы и перемещения, возникающие после удара.

При определенных предположениях можно найти силу, статически прикладываемую в точке удара, чтобы вызвать наибольшое динамическое перемещение системы. Такую силу обычно называют динамической .

Продольный удар

При забивки свай тяжелый груз падает с некоторой высоты на верхний торец сваи и погружает её в грунт; груз останавливается мгновенно, вызывая удар. За время удара между обеими ударяющими деталями возникают большие взаимные давления. Скорость ударяющегося тела за очень короткий промежуток времени изменяется и в данном случае падает до нуля. На него от ударяемого тела передается реакция , направленная в сторону, обратную его давлению.

По закону равенства действия и противодействия на ударяемую часть конструкции передается такая же сила, но обратно направленная. Эти силы вызывают напряжения в обеих телах.

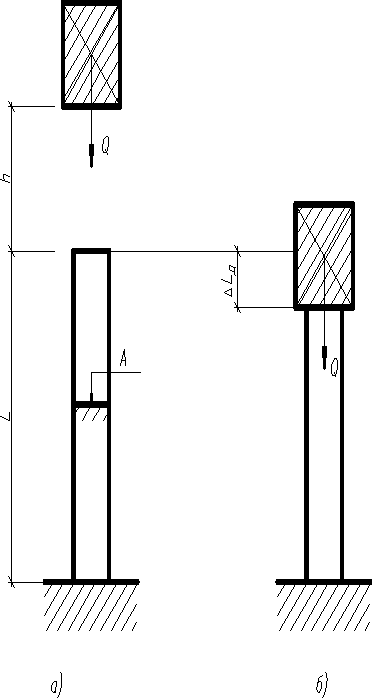
Пусть, груз с весом без начальной скорости, падает на неподвижный стержень с высоты (рис.а)). Если пренебречь сопротивлением движению, то скорость тела в момент удара . Эта скорость за время удара упадет до нуля. Получающиеся большие ускорения (замедления) приводят к возникновению значительных инерционных сил, которые и определяют действие удара. Т.к. неизвестно, то установить закон изменения скорости и силу инерции теоретически весьма затруднительно. Поэтому для определения перемещений и напряжений, вызванных действием ударных нагрузок, пользуются энергетическим методом, основанным на законе сохранения энергии и следующих допущениях:

Напряжения в ударном элементе не превосходят предела пропорциональности, и закон Гука сохраняет свою силу;
Тела после удара не отделяются друг от друга;
Ударяющее тело является абсолютно жестким и не деформируется;
Потерей части энергии, переходящей в теплоту и в энергию колебательного движения соударяющихся тел пренебрегаем;
Масса ударяемого элемента мала по сравнению с массой ударяющего тела и в расчет не принимается.

Кинетическая энергия падающего груза, численно равна работе, совершаемой им при падении и деформации стержня: , где - перемещение в точке удара, равное укорочению стержня. Потенциальная энергия деформации стержня при сжатии . Здесь в соответствии с законом Гука , откуда . Пользуясь законом сохранения энергии и пренебрегая потерями энергии, вызванными местными пластическими деформациями при соударении тел можно записать или . Откуда . Разделив все члены полученного уравнения на и учитывая, что -укорочение стержня от статически приложенной нагрузки будем иметь квадратное уравнение , решив которое найдем . Оставляя знак плюс (решение со знаком минус перед радикалом противоречит физическому смыслу задачи), получим окончательно

(2)

где - динамический коэффициент.

Разделив обе части (2) на длину стержня и умножив на модуль упругости Е, перейдем на основании закона Гука от деформаций к напряжениям

(3).

Видим, что динамические напряжения и перемещения зависят от статической деформации ударяемого тела. Чем больше (при прочих равных условиях), тем меньше и . Поэтому для смягчения удара применяют прокладки (резиновые, пружинные) дающие больше деформации. При ударе условие прочности имеет вид , но кроме этого при сжатии стержня во избежание продольного изгиба , где -критическое напряжение.

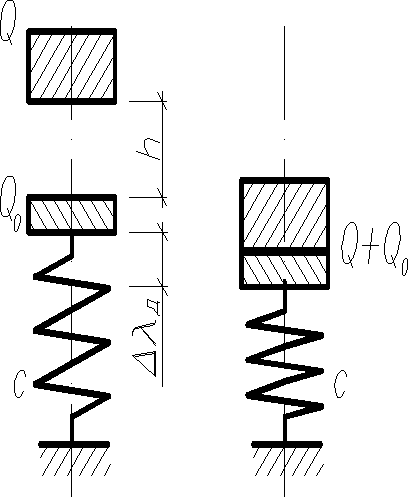
Рассмотрим случай:

- жесткость пружины (сила, вызывающие смещение на единицу длины).

(1)

После удара, вследствие полученной начальной скорости пружина сожмется на величину

(2), или

. (3)

После соприкосновения тела как бы слипаются и продолжают совместное движение со скоростью , сжимая пружину.

По теореме об изменения количества движения получим

(4), откуда (6)

Пружина продолжает сжиматься, а скорости тел уменьшается. Сила сжатия пружины достигает при . Воспользуемся теоремой об изменений кинетической энергий

(6)

- кинетическая энергия в момент наибольшего сжатия пружины ;

- энергия после удара в начальный момент движения;

- работа всех сил на пути .

(7)

Сила тяжести на пути совершает работу .

Со стороны пружины на тела действует переменная сила.

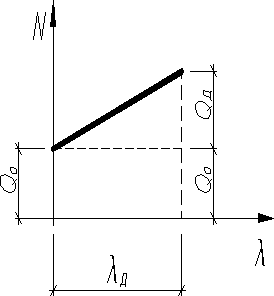
(8)

(7) и (8) подставим в (6)

(9)

, ,

, где .

Если тело падает на невесомую, т.е., то .

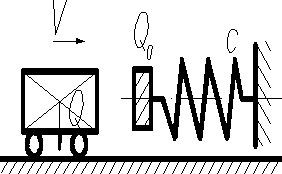
Аналогичное решение можно получать и для горизонтального удара

, с другой стороны , тогда

Поперечный удар

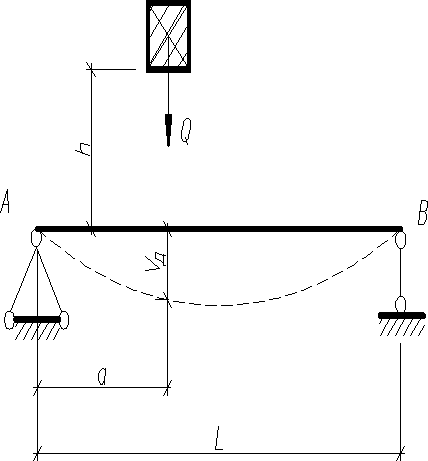
Аналогичные формулы можно получить и для случая поперечного (изгибающего) удара. Только в этом случае вместо следует принимать статический изгиб балки - в месте удара, а вместо динамический прогиб .

Частный случай: Если h=0, т.е. имеет место внезапное приложение нагрузки, то из (2) и (3) получим деформации и напряжения, вдвое больше, чем при статическом действии: , .

Когда масса ударяемой конструкции не мала по сравнению с массой ударяющего тела, то им пренебречь нельзя. В этом случае динамический коэффициент определяется по формуле

(4)

где -статическая деформация (,) в точке падения груза;

-полный вес ударяемого тела; -коэффициент приведения равный, при растягивающем (сжимающем) ударе и при изгибающем ударе в середине пролета простой балки.

Учет массы ударяемого элемента приводит к уменьшению величины динамического коэффициента, т.е. к снижению эффекта удара ( по (4) меньше ).

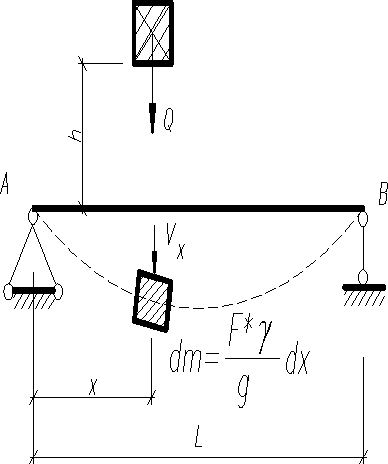
Для определения кинетической энергии системы, предположим, что скорость элемента балки, отстоящего от левой опоры на расстоянии пропорциональна перемещению этого сечения от статической нагрузки, приложенной в виде силы Р в точке удара. Это условие пропорциональности можно выразить . Здесь - соответственно скорость и прогиб в середине пролета.

Приняв, что точка удара расположена в середине балки, будем иметь следующее уравнение прогибов:

Следовательно

, .

Кинетическая энергия системы будет определяться равенством

Найдем теперь кинетическую энергию для балки, у которой посредине пролета прикреплена приведенная масса. Считая, что скорость движения этой массы будет равна величине , получим

Две системы можно считать эквивалентными друг другу, если у них количество будут одинаковыми. Если приравнять два полученных выше выражения для энергий, то легко заметить, что коэффициент будет определяться равенством

Подставим найденное значение в формулу динамического коэффициента. Тогда для балки на двух опорах при ударе падающим грузом в точку, расположенную посередине пролета, получим

-прогиб балки в точке удара от статического действия груза;

- вес балки;

h – высота падения;

G – вес падающего груза.

Приближенный учет распределенной массы

; ; ;

при ;

при

;

, ;

;

, получим, что

Динамическая нагрузка