Основные результаты теории кручения сплошных прямых стержней некруглого поперечного сечения
Основные результаты теории кручения сплошных прямых стержней некруглого поперечного сечения.
В инженерной практике кручению подвергаются стержни, имеющие прямоугольное, треугольное, эллиптическое и другие сечения. В этих случаях сечения искривляются (депланируются). Следовательно, напряженное состояние не может быть определено введением упрощающих гипотез типа гипотезы плоских сечений. Задачи решаются методами теории упругости. Приведем основные результаты решения для некоторых наиболее часто встречающихся форм поперечных сечений стержней, при свободном кручении.
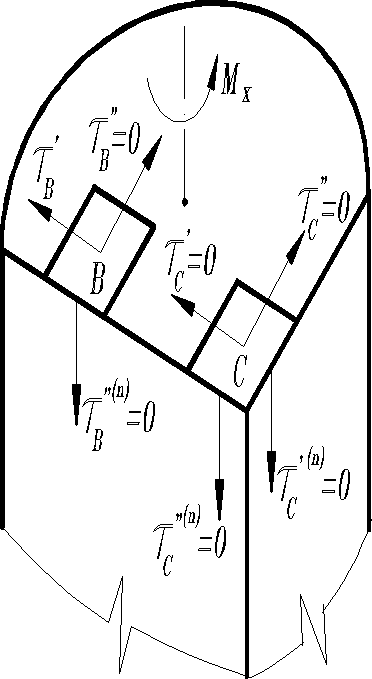
Отметим, что в стержне произвольного сечения касательные напряжения вблизи точек контура направлены по касательной к нему. Действительно, предположим, полное напряжение вблизи точки В представлено двумя составляющими:
- По касательной к контуру ;
- По нормали .
В силу закона равновесия на свободной поверхности стержня должно действовать напряжение . Но по условию задачи на этой поверхности нагрузка и внешние силы отсутствуют, т.е. . Следовательно, , и касательная напряжения . Аналогично можно показать, что если контур поперечного сечения имеет угловую точку, например С (см. рис.), что в окрестности нее .
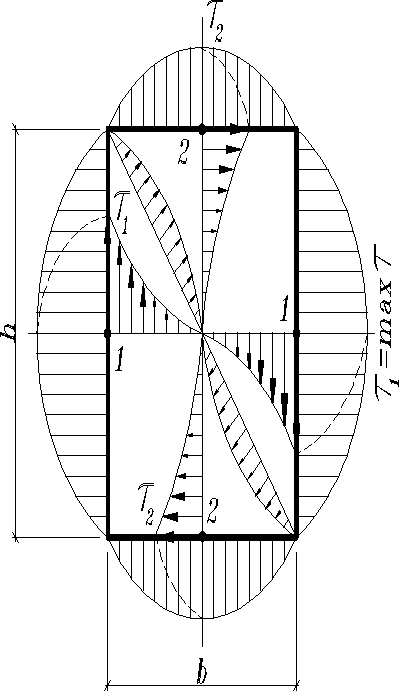
Прямоугольное поперечное сечение, . По центральным прямым распределяются нелинейно. Наибольшие напряжения возникают у поверхности посредине длинных сторон вблизи точек 1 и определяются по формуле
(1)
Напряжение посредине коротких сторон меньше и выражаются через следующим образом
(2)
Относительный угол закручивания вычисляется из выражения
(3)
а угол поворота сечения аппликатой относительно сечения с аппликатой равен
(4)
|
1 |
1,5 |
1,75 |
2 |
2,5 |
3 |
4 |
6 |
8 |
10 |
||
|
0,208 |
0,231 |
0,239 |
0,246 |
0,258 |
0,267 |
0,282 |
0,299 |
0,301 |
0,313 |
0,333 |
|
|
0,141 |
0,196 |
0,214 |
0,229 |
0,249 |
0,263 |
0,281 |
0,299 |
0,307 |
0,313 |
0,333 |
|
|
1,00 |
0,859 |
0,820 |
0,795 |
0,766 |
0,753 |
0,745 |
0,743 |
0,742 |
0,742 |
0,743 |
При , то с большой точностью можно принять . Тогда
; ; .
При этом распределение по толщине стержня приближается к линейному. В формулах (1), (3), (4)
(5) (6)
есть некоторые геометрические характеристики, которые можно по аналогии со стержнем круглого поперечного сечения назвать моментом сопротивления и условным моментом инерции при кручении.
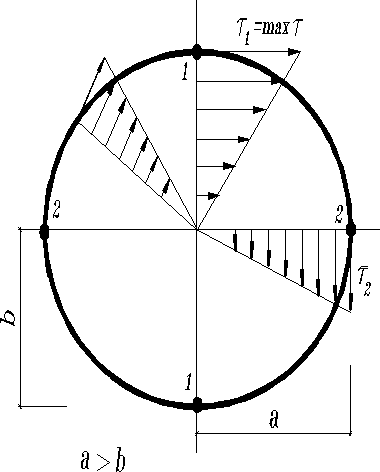
Для эллиптического сечения
(7)
(8)
(9) (10)
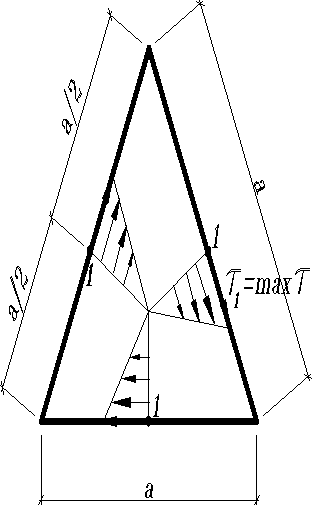
Для сечения имеющего форму равностороннего треугольника со сторонами , имеем
(11)
(12) (13)
здесь ; .
Свободное кручение тонкостенных прямых стержней открытого профиля.
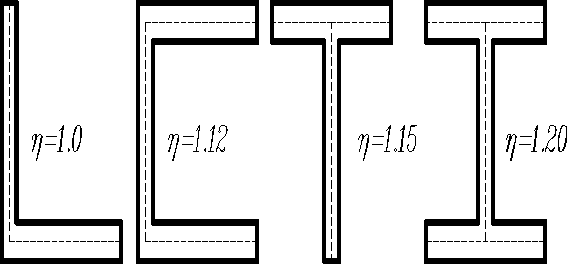
Теория расчета на кручение стержней прямоугольного попе-речного сечения используются для приближенного решения задачи о кручении тонкостенных стержней незамкнутых профилей, которых можно представит в виде нескольких узких прямоугольников. Геометрическое место точек, которые расположены в середине толщин стенок элемента, образует среднюю линию. У стержней открытого профиля эта линия незамкнута. Элемент называется тонкостенным при условии , где - длина средней линии и толщина стенки любого из прямоугольников, составляющих поперечное сечение.
Поставим задачу: Определить наибольшее касательное напряжение , относительный угол закручивания и угол поворота при свободном кручении тонкостенного стержня открытого профиля.
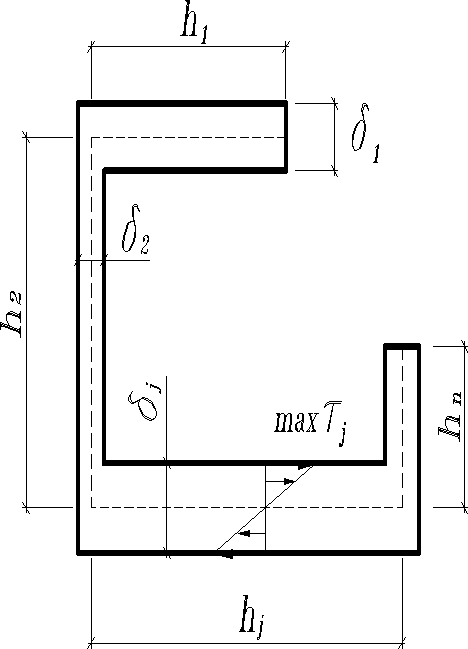
Разделим поперечное сечение на прямоугольников. Пусть на первый из них передается крутящий момент , на второй ,…, на j-тый , на -ый . Тогда момент воспринимаемый всем сечением, будет равен
(а)
Если принять допущение, что профиль при деформации не изменяет свою форму, то относительные углы закручивания и углы поворота всех частей элемента следует считать одинаковыми
(б)
(в)
Каждый участок сечения является прямоугольником, для которого
(г); (д)
Откуда ;;…;
и подставляя в (а) найдем . Теперь из (1)
(14)
Из (б) и (г)
(15)
из (в) и (д) (16)
Следовательно (см. (14)) наибольшие касательные напряжения возникают вблизи точек контура, расположенных посредине длинной стороны участка с наибольшей толщиной стенки
(17)
В выражениях (15) и (17)
(18)
(19)
есть момент сопротивления и условный момент инерции поперечного сечения стержня при кручении.
Изложенный способ определения , как отмечалось, является приближенным, поскольку не учитывается переменность толщины отдельных элементов профиля, повышение и внутренних углов и другие факторы. Заметим, что во избежании местных перенапряжений эти углы выполняются округленными.
Понятие о пленочной (мембранной) аналогии
Для исследования напряженного состояния сложных профилей и уточнения результатов расчетов при кручении применяют косвенные методы, среди которых важнейшим является метод аналогии.
В механики встречаются случаи, когда совершенно различные по физической сущности задачи сводятся к одним и тем же дифференциальным уравнениям. Тогда между задачами может быть установлена аналогия. Оказывается, что независимо от формы исследуемого сечения, распределение напряжений при кручении сводится к дифференциальному уравнению, которым определяется равновесие пленки (мембраны), натянутой по контуру того же очертания и нагруженной равномерно распределенным давлением. Аналогом напряжений является угол , образованный плоскостью контура с касательной к поверхности пленки, а аналогом крутящего момента - объем V, заключенный между плоскостью контура и поверхностью пленки.
Пусть требуется установить закон распределения в сечении. Представим, что на заданный контур натянута мембрана, нагруженная равномерным давлением. С помощью пленочной аналогии получают и количественные значения , и в различных сечениях при кручении. В частности , более точная формула для определения условного момента инерции стержня открытого профиля
где -поправочный коэффициент, зависящий от формы профиля.
Свободное кручение тонкостенных прямых стержней закрытого профиля
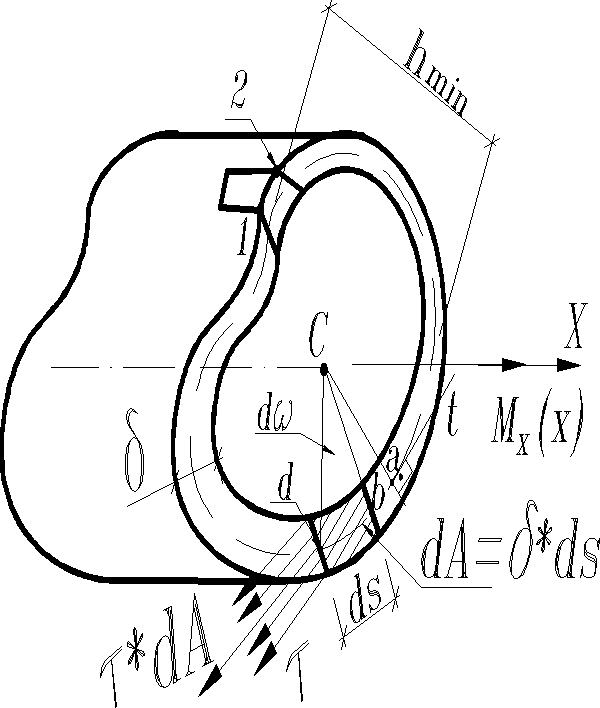
Тонкостенный цилиндри-ческий стержень с замкнутой средней линией для которого выполняется условие (- минималь-ный поперечный размер, - наибольшая толщина профиля). Считаем плавно изменяющейся вдоль контура. Определим касательные напряжения и угловые дефор-мации.
Ось Х совместим с осью кручения, представляющей совокупность точек (центров кручения), вокруг которых происходят повороты сечений.
В виду незначительной толщины стенки принимается допущение о том, что напряжения по толщине распределяются равномерно и направлены по касательной к средней линии (гипотеза Р.Бредта).
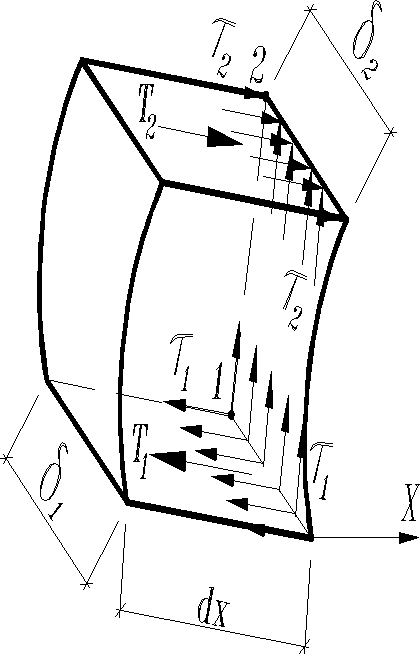
Из стержня мысленно выделим элемент длиной dx. Пусть толщина контура в месте 1 будет , а в месте 2-. Соответственно через и обозначим напряжения в поперечном сечении. По закону равновесия касательных сил в продольных сечениях возникают также равномерно распределенные напряжения и , равнодействующие которых и .
.
Т.к. места 1 и 2 взяты произвольно, то (а)
Следовательно: 1) произведение (поток напряжений) для замкнутого контура не изменяется; 2) наибольшее напряжение там, где толщина наименьшая.
Заметим, что в рассматриваемом случае касательные напряжения являются аналогом скоростей идеальной (не имеющей трения) жидкости, а поток напряжений - аналогом расхода этой жидкости, при движении ее в лотке, имеющем профиль и размеры одинаковые с поперечным сечением тонкостенного стержня ( - совпадает по направлению с постоянны по ширине лотка , -гидродинамическая аналогией.
Момент силы , воспринимаемый элементом поперечного сечения длиной ds, относительно центра кручения С равен . Тогда уравнение запишется в виде . Но , а произведение представляет уравнение удвоенную площадь элементарного треугольника , т.е. . Поэтому
или . Откуда (20)
где -площадь, ограниченная средней линией контура..
Наибольшее напряжение будет в том месте, где толщина стенки минимальная
(21)
где - момент сопротивления стержня закрытого профиля кручению.
Определим угловое перемещение , полагая внешние пары статически приложенными только к торцам стержня. Работы этих пар определяется из выражения и по закону сохранения энергии равна полной потенциальной энергии деформации
(б)
С другой стороны при чистом сдвиге удельная и накопленная в элементарном объеме с размерами энергия соответственно равны и . Проинтегрировав последнее уравнение по длине стержня и по замкнутому контуру, при постоянном поперечном сечении вдоль оси Х получим
Интеграл зависит от закона изменения толщины по контуру и является геометрической характеристикой. Учитывая, что , получим
(в)
Приравнивая правые части формул (б) и (в) найдем
(22)
Относительный угол закручивания
(23)
здесь - есть условный момент инерции сечения стержня при кручении.
Если , например, тонкостенная труба с радиусом средней линии , то , . По формулам (21), (22), (23)
; ; .
Расчеты на прочность и жесткость стержней некруглого поперечного сечения
Условие прочности при расчете по допускаемым напряжениям
(24)
- наибольший по абсолютной величине крутящий момент;
-момент сопротивления при кручении вычисляемый в зависимости от типа профиля;
- допускаемое касательное напряжение.
Условие жесткости
(25)
- наибольший крутящий момент от нормативной нагрузки;
- условный момент инерции поперечного сечения стержня при кручении;
- допускаемый относительный угол закручивания.
Основные результаты теории кручения сплошных прямых стержней некруглого поперечного сечения