Сложное сопротивление прямого призматического стержня
Сложное сопротивление прямого призматического стержня.
На практике многие элементы конструкций и машин испытывают не одну из простейших деформаций (центральное растяжение и сжатие, кручение, плоский изгиб) а две и более. Валы машин подвергаются кручение и изгибу; мачты, трубы, вышки, колонны – сжимаются собственным весом и изгибаются, например, давлением ветра и т.д. Случаи сопротивления элементов сочетанию двух или более простых напряженных состояний называются сложным сопротивлением.
Задача определения напряжений при сложном сопротивлении стержня сплошного поперечного сечения решается в соответствии с принципом суперпозиции, если: а) материал подчиняется закону Гука; б) деформация малы по сравнению с поперечными размерами, т.е. стержень жесткий. Зоны концентрации напряжений, а также места вблизи точек приложения сил, исключаются. Рассматриваются прямые призматические стержни, центр изгиба которых совпадает с центром тяжести поперечного сечения. Строятся эпюры внешних усилий по длине стержня и устанавливается положение наиболее опасного сечения.
В общем случае сложного напряженного состояния приложенные к исследуемой части элементы внешние силы могут быть представлены тремя составляющими главного вектора (продольной N и поперечными силами) и тремя составляющими главного момента (крутящим и изгибающими момента).
; ; ; ;
; ;
{с помощью уравнений равновесия}
;
;
;
;
;
;
- вызывают в сечении нормальные напряжения, а - касательные напряжения.
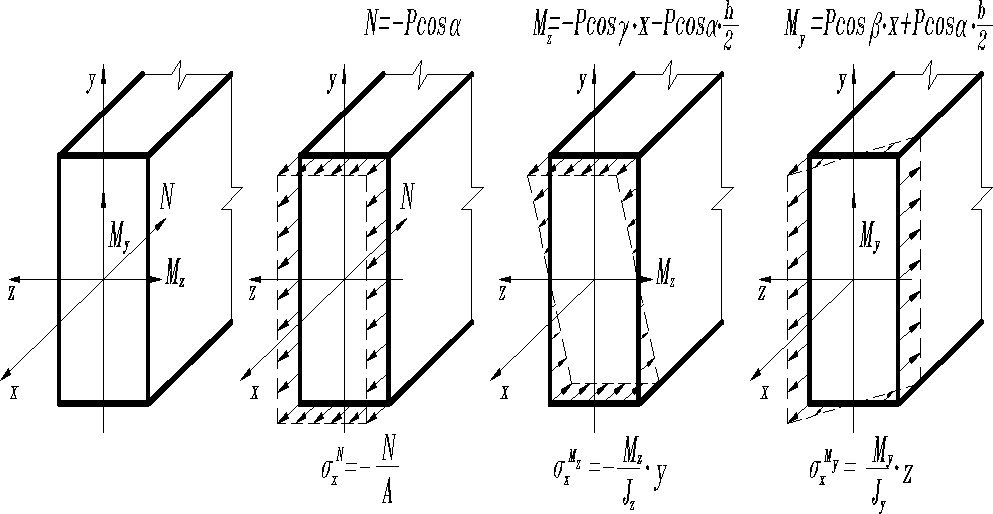
От продольной силы нормальные напряжения равномерно распределены по всему сечению и равны
.
Нормальные напряжения, обусловленные действием изгибающих моментов , находим по формулам
, ,
где и - координаты точки, вблизи которой вычисляется напряжение;
и - главные центральные моменты инерции поперечного сечения стержня.
Применяя принцип суперпозиции, получим полное нормальное напряжение вблизи рассматриваемой точки
(1)
Полагая в (1) и будем иметь уравнение нейтральной линии
.
- напряжение при центральном растяжении (сжатии);
тогда
Отрезки, отсекаемые нейтральной линии на координатных осях равны:
при , (а)
при . (б)
Так как наличие или отсутствие в уравнениях (а) и (б) члена не меняет наклона нейтральной линии к осям координат, то для определения последнего можно воспользоваться уравнением, из которого следует, что
(2)
Складывая геометрически моменты и , действующие в сечении в плоскостях “XY” и “XZ”, найдём величину результирующего изгибающего момента
Угол между плоскостью действия и вертикальной плоскостью “XY” найдём из выражения , тогда .
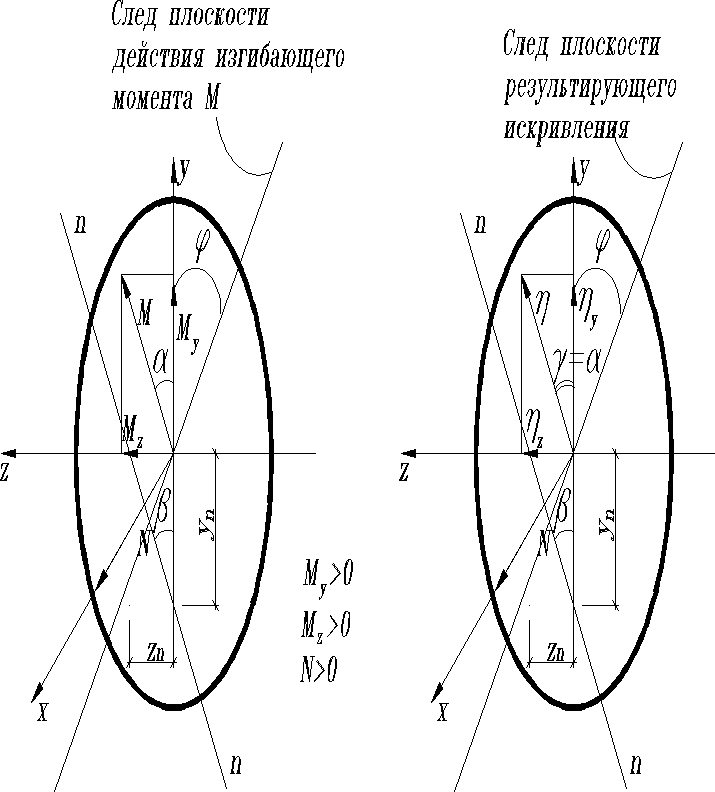
Углы и будем считать положительными, если они откладываются от соответствующих осей ( от оси , а от оси ) против направления вращения часовой стрелки.
Из выражений а) и б) видно, что нейтральная линия в сечении в общем случае не перпендикулярна к следу плоскости действия в том же сечении результирующего изгибающего момента. Эти линии будут перпендикулярны лишь при условии равенства углов и , а это в свою очередь возможно только в следующих случаях: 1) , т.е. ; 2) , т.е. ; 3) .
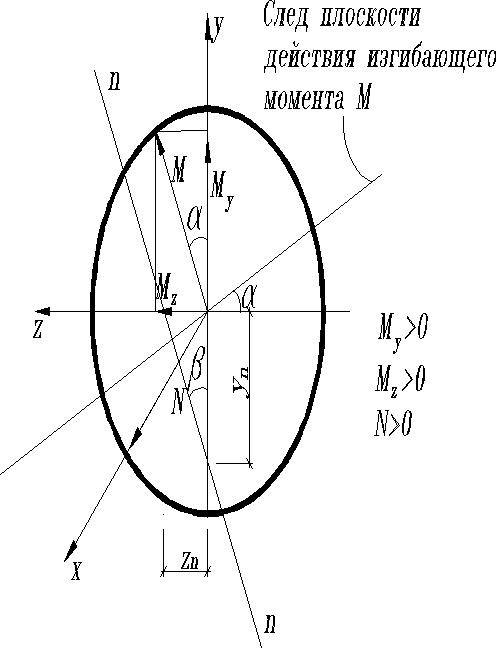
В случаях 1) и 2) независимо от значения и - главных моментов инерции, имеет место плоский изгиб в одной из главных плоскостей инерции стержня, а в случае 3) все оси инерции будут главными центральными осями инерции (круг, квадрат и др.) и изгиб в любом направлении будет плоским.
Общий вывод: Изгиб плоским и нейтральная линия будет перпендикулярна к следу плоскости действия результирующего изгибающего момента, если эта плоскость пересечёт сечение перпендикулярно к одной из главных центральных осей инерции.
Вблизи наиболее удаленных от нейтральной линии точек 1 и 3 возникает наибольшие растягивающие и сжимающие напряжения, которые определяются с подстановкой в (1) координат этих точек.
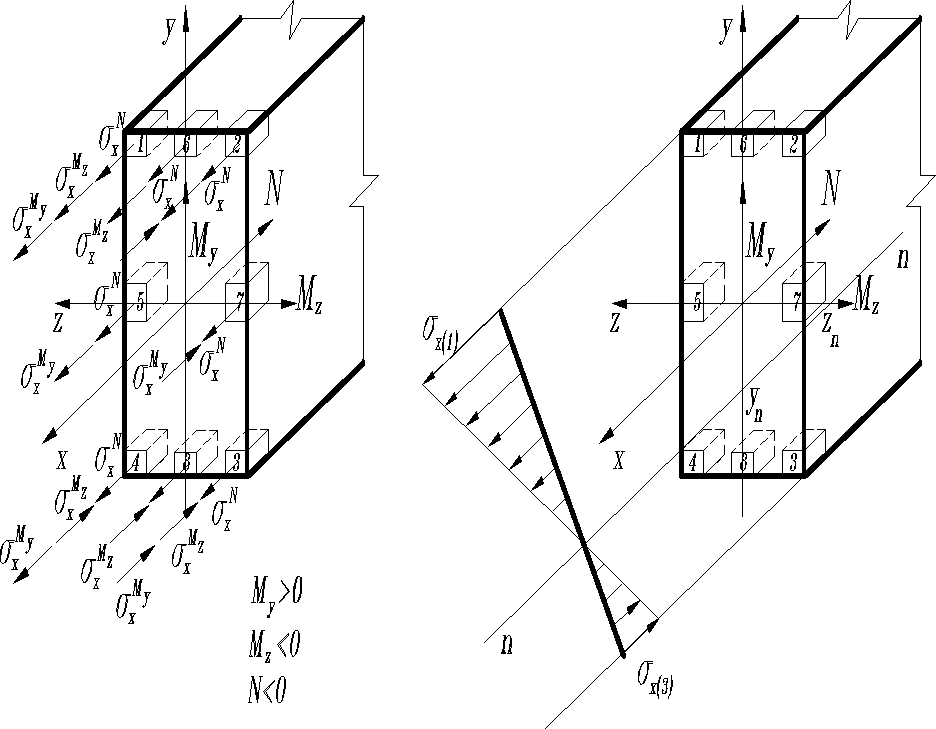
От действия поперечных сил и касательные напряжения находятся по формуле Д.И.Журавского: и . Здесь и - статически моменты относительно главных центральных осей инерции и частей поперечного сечения площадью и , расположенных выше (или ниже) и слева (или справа) от рассматриваемой точки с координатами и ; и - ширина, и высота профиля на уровне и .
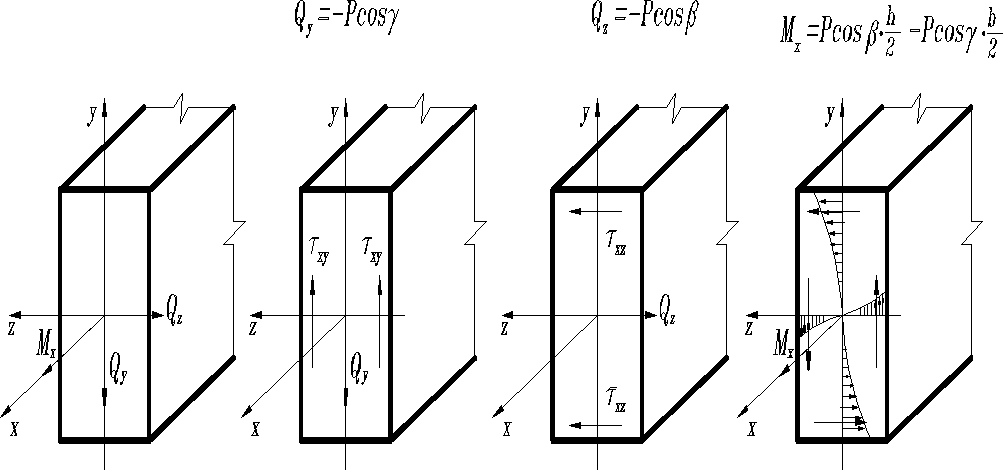
; при
; при
От при свободном кручении появляются только касательные напряжения
. Закон их распределения в общем случае сложен. Для стержня сплошного круглого поперечного сечения эти напряжения вычисляются по формуле . Для элементов другой формы используется выражение
, .
Во всех случаях наибольшие касательные напряжения имеют место вблизи точек контура и направлены по касательной к контуру.
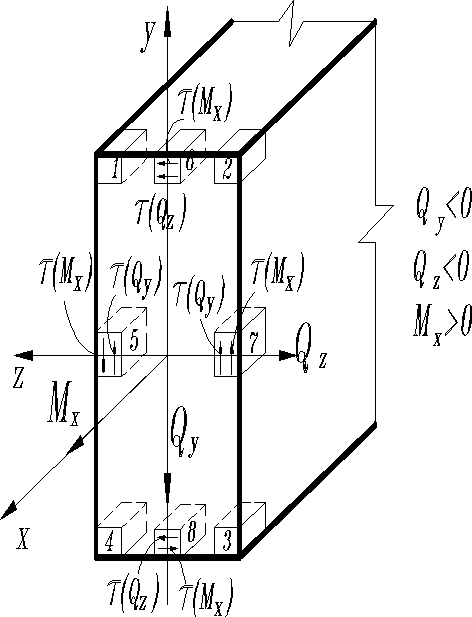
Суммарные достигают наибольшего значения в центре тяжести сечения, где касательные напряжения от кручения и нормальные напряжения от изгиба и равны нулю. Поэтому часто не имеют практического значения. Т.к. и принимают наибольшие значения на контуре, то там обычно разыскиваются опасные точки, вблизи которых получаются наиболее неблагоприятные сочетания и , производится проверка прочности материала стержня. Такими могут быть: точки с , точки с или промежуточные точки контура. При необходимости, например в стержне прямоугольного поперечного сечения, учитываются также и касательные напряжения и , получая полные и геометрическим суммированием , .
Для проверки прочности материала необходимо рассмотреть сочетание и вблизи опасных точек, вычислить в них полные нормальные и касательные напряжения, затем главные напряжения . Далее, применяя одну из гипотез прочности, определить приведенное напряжение и наконец, проверить удовлетворяется ли условие прочности .
Например, для точки 5.
Например, для точки 5.
Круглое поперечное сечение
Наибольшие нормальные напряжения возникают в точках В и С, расположенных на перпендикуляре к вектору полного изгибающего момента и определяется по формулам:
, где .
Касательные напряжения в точках В и С:
;
;
, где - проекция поперечных сил на вектор полного изгибающего момента .
В этих точках касательные напряжения от кручения достигают наибольших значений. От поперечных сил касательные напряжения обычно меньше и значительно меньше нормальных напряжений в этих точках.
Перемещение стержня.
Поперечные сечения элемента перемещаются поступательно вдоль осей Х, Y, Z (от ), поворачиваются относительно этих же осей (от ,) и искривляются (от , , ). Определить перемещения любой точки сечения в общем случае напряженного состояния можно только методами теории упругости. Поэтому в сопротивлении материалов эта задача ограничивается нахождением перемещений точек оси стержня , тангенсов углов наклона касательных к оси изогнутой оси и углов закручивания сечений . При этом применяется принцип суперпозиции: компоненты деформации вычисляются от отдельных групп сил независимо от других и затем геометрически складываются.
Перемещение конца консоли в направлении оси “Х” определяем с помощью выражения
.
Угол поворота конца консоли относительно оси “Х” равен углу закручивания
; где ;
момент инерции при кручении для:
прямоугольника при ; при ;
круглого поперечного сечения ;
Дифференциальное уравнение (изгиба) оси изогнутой балки в вертикальной плоскости
;
после определения постоянных интегрирования С и D, вычисляем составляющую полного перемещения по оси “У” конца консоли , и угол поворота относительно оси “Z” .
Дифференциальное уравнение (изгиба) оси изогнутой балки в горизонтальной плоскости
;
после определения постоянных интегрирования С и D, вычисляем составляющую полного перемещения конца консоли по оси “Z” по формуле , и угол поворота относительно оси “У” .
Полное перемещение
В общем случае сложного сопротивления стержня, в числе других простых деформаций подвергается двум плоским изгибам в главных плоскостях инерции, упругая линия стержня, вообще говоря, будет представлять собой пространственную кривую. При этом кривизна упругой линии в плоскости “XY” (вертикальной) будет равна
(А)
а в плоскости “XZ” (горизонтальной) будет равна
(В)
Если отложить векторы кривизны и на соответствующих осях координат, то вектор полной кривизны упругой линии , представляющий их геометрическую сумму будет направлен под углом к оси “Y”, тангенс которого равен
(3)
Сравнивая (2) и (3) убеждаемся, что углы и равны между собой, т.е. вектор полной кривизны параллелен нейтральной линии, а при отсутствии нормальной силы совпадает с нею. Вследствие этого плоскость результирующего искривления, перпендикулярная к вектору полной кривизны и касательная к упругой линии стержня в данном сечении, всегда перпендикулярна к нейтральной линии. Направление же перемещения центра тяжести рассматриваемого сечения будет перпендикулярна к нейтральной линии только при изгибе в одной плоскости (при и на протяжении всей длины стержня – например, при плоском и косом изгибе).
При (см. рис.) и , т.е. направление перемещения центра тяжести сечения отклоняется от плоскости действия к оси “Y”. Нетрудно заметить, что направление перемещения всегда будет отклоняться от плоскости действия результирующего изгибающего момента в сторону оси с наибольшим моментом инерции.
Применяя принцип сложения действия сил, для нахождения полного перемещения центра тяжести поперечного сечения стержня, можно воспользоваться дифференциальными уравнениями (А) и (В) упругой линии. После интегрирования их с последующим нахождением постоянных интегрирования из граничных условий и определения в данном сечении двух составляющих перемещения и в направлении главных осей инерции “Y” и “Z” величину полного перемещения найдем как их геометрическую сумму .
Вариант II. Для определения перемещений применяем теорему Кастильяно. Потенциальную энергию деформации стержня представим в виде функции всех шести компонентов сил: . Пренебрегая энергией касательных напряжений сдвига
;
;
;
Значок показывает, что интегрирование распространяется на длину такого участка стержня, на протяжении которого функции координаты , т.е. остаются непрерывными. При наличии в стержне нескольких таких участков вместо одного интеграла нужно вычислить интегралы по каждому из участков и взять их сумму.
Применяя теорему Кастильяно, искомые перемещение в направлении какой либо из сил находим из выражении
Под и здесь, понимается обобщённое усилие и соответствующее этому усилию, обобщённое перемещение. Аналогично составляются формулы Мора и Верещагина.
Дополнительно:
В случае а)
В случае в)
;
;
;
;
;
;
;
;
;
;
;
;
Сложное сопротивление прямого призматического стержня