Центральное растяжение и сжатие

а) Чистое центральное растяжение (сжатие) прямого стержня

Допустим, что в продольных сечениях стержня напряжения отсутствуют:

, а в поперечном сечении нормальные напряжения распределяются равномерно

, (а)

и нет касательных напряжений

. (в)

Начало координатных осей совместим с центром тяжести поперечного сечения бруса, т.е. зададимся центральными осями координат, для которых

(с)

Выясним, какими внешними силами создается заданное напряженное состояние.

Подставив (а) и (в) в (1)-(6)-(уравнения равновесия), будем иметь:

(1) (d)

(2)

(3)

(4)

(5)

(6) .

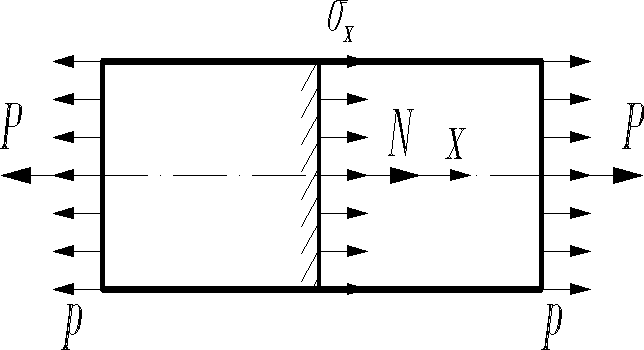
Таким образом, внешние силы приводятся к продольной силе. Т.к. внутренние силы, представленные напряжениями , распределяются по сечению равномерно, то и интенсивность внешних сил , приложенных по торцам бруса, должна быть постоянной и равной по модулю. Задавшись направлением сил от торца, т.е. создавая растяжение стержня, будем иметь случай, представленный на рис.1.

Равнодействующую сил обозначим , она должна совпадать с продольной осью бруса и действовать в направлении сил . Напомним, что продольная сила есть проекция на ось X главного вектора внешних, приложенных к отделенной части тела. При выборе (1.1) полагались, что совпадает по направлению с осью X. В рассматриваемом случае (для левой части стержня) имеем , т.к. направление силы и оси X не совпадают. Тогда выражение (d) примет вид . Откуда (1).

В случае сжатия ( направлены в торец), равнодействующая вводится в (1) со знаком минус. Т.о. при растяжении , при сжатии .

Напряженное состояние, при котором внешние силы распределяются равномерно по торцам бруса и приводятся к продольной силе, а во всех поперечных сечениях возникают только нормальные напряжения и , называется чистым центральным растяжением (сжатием).

Признак чистого центрального растяжения: внешние силы приводятся к продольной силе.

Условие чистого центрального растяжения: внешние силы по торцам распределены равномерно.

Условие прочности при центральном растяжении записывается в виде

. (2)

где - допускаемое напряжение (расчетное сопротивление), установленное для материала, из которого изготовлен элемент. Формула (2) служит как для проверки прочности элемента при центральном растяжении (сжатии), так и для подбора площади поперечного сечения A при заданной силе и принятом для изготовления элемента материала.

б) Нечистое центральное растяжение стержня. Принцип Сен – Венана.

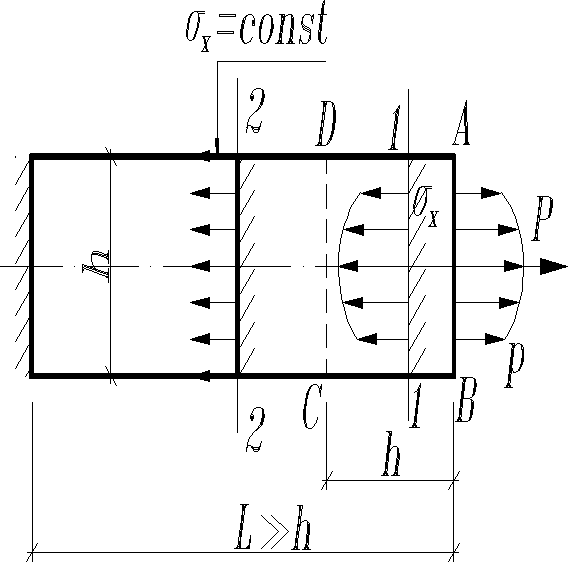
Когда силы распределены по торцам неравномерно, но приводятся к равнодействующей , линия действия которой совпадает с продольной осью бруса, имеем нечистого центрального растяжения (сжатия). Если длина элемента (поперечный размер) то, как показывают исследования в сечениях I-I, расположенных вблизи торца АВ бруса напряжения . В сечениях же 2-2 достаточно удаленных от торца напряжения определяются в соответствии с принципом Сен-Венана, заключающемся в следующем:

Если внешние силы распределены на небольшой части тела, то замена заданных сил статически эквивалентными не влияет на характер распределения внутренних сил в сечениях достаточно удаленных от места приложения внешних сил.

В рассматриваемом случае (рис.2) в сечении 2-2 напряжения и их можно определять по формуле (1) чистого центрального растяжения (сжатия).

За достаточное считается удаление, равное полному размеру загруженного участка (торца) поверхности тела.

Статически эквивалентные силы имеют одинаковые главный вектор и момент.

Принцип Сен-Венана во многих случаях может существенно упростить расчет. Например, нагрузка от колеса машины на мостовую балку, распределенную по площади контакта по довольно сложному закону, можно заменит сосредоточенной силой , что мало повлияет на усилие в местах, удаленных от площади контакта.

Замечание: при для вычисления формулу (1) применять нельзя, в этом случае расчет представляет весьма сложную задачу.

При сжатии достаточно длинных (гибких) стержней может произойти их искривление (потери устойчивости). Этого явления следует избегать, проектируя, жесткие стержни, либо выполнив соответствующий расчет на устойчивость.

в) Закон Гука при центральном растяжении (сжатии) прямого стержня.

Рассмотрим прямой призматический стержень, длина которого до приложения сил , поперечные размеры . Считаем, что материал стержня однородный, изотропный и идеально упругий. Зададимся координатными осями ХОУ (оси Z направлены в сторону наблюдателя). Приложим к торцам элемента статически равномерно распределенные силы,

интенсивностью , равнодействующая которых возрастала от нуля до значения . Осуществляется чистое центральное растяжение.

Длина бруса увеличится и станет равной , поперечные размеры уменьшатся до . Полная абсолютная линейная деформация в продольном направлении будет , в поперечных - и , а относительные линейные деформации по тем же направлениям соответственно

(е)

(к)

Опытами установлено, что:

Абсолютная продольная деформация прямо пропорционально приложенной силе и первоначальной длине и обратно - пропорциональна площади поперечного сечения элемента А, т.е.

(3) или (3’)

где -коэффициент жесткости; -жесткость стержня.

Относительная поперечная деформация прямо пропорциональна относительной продольной деформации

(4)

Стержень в деформированном состоянии остается прямоугольным, форма тела не изменяется, угловых деформаций нет.

Зависимость (3) называется законом Гука в абсолютных единицах. Учитывая и , выражение (3) приводим к виду

(5)

Относительные деформации можно представить в виде

(6)

Зависимости (6) называются законом Гука в относительных единицах в случае равномерного растяжения (сжатия) призматического стержня вдоль продольной оси.

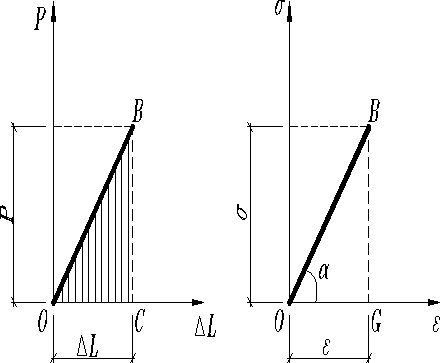
Связь между

можно представить графиками

называемыми диаграммами.

г) Упругие характеристики материалов

Коэффициент пропорциональности Е, входящий в выражения (3), (5), (6) называется модулем упругости или модулем Юнга. Модуль Е - одна из констант материала, измеряемая в единицах напряжения Па, МПа (следует из (5)). Чем больше модуль упругости, тем меньше деформируется стержень при прочих равных условиях (), т.е. он характеризует сопротивление материалов упругой деформации при растяжении (сжатии) и является мерой жесткости материала. Из графика представленного на рис. следует, что модуль Е пропорционален углу наклона участка диаграммы к оси абсцисс.

здесь -масштабы напряжений и деформаций в которых выполнена диаграмма.

Коэффициент пропорциональности , равный абсолютной величине отношения относительной поперечной деформации к относительной продольной деформации

(7)

принято называть коэффициентом поперечной деформации или коэффициентом Пуассона. Коэффициент , также как и модуль Е, является характеристикой упругих свойств материала.

Модуль упругости и коэффициент Пуассона определяется экспериментально из выражений

Для условно упругих изотропных материалов имеем две упругие характеристики Е и (), для анизотропных - несколько. Во многих практических случаях принято считать, что модуль упругости и коэффициент Пуассона при растяжении и сжатии материала одинаковые. Значения Е и и допускаемое напряжение (расчетное сопротивление) для некоторых материалов при температуре 200 представлены в таблице.

Характеристика материала	материал
	Сталь	чугун	алюминий	бетон	Сосна вдоль волокон
	1.92.2	0.951.05	0.70.8	0.150.4	0.10.12
=R		2880 120150	3080	0.71.4 8.025.0	710 1012
	0.240.33	0.230.25	0.320.36	0.10.2	-

д) Изменение объёма стержня при его центральном растяжении (сжатии).

[Обобщенный закон Гука].

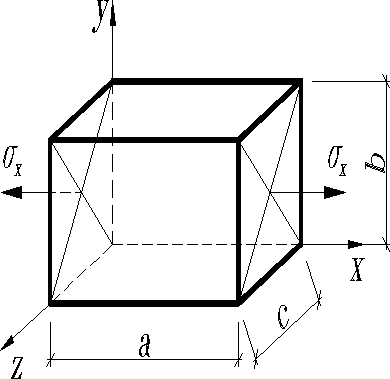
Выделим в стержне, выполненном из материала подчиняющегося закону Гука, прямоугольный параллелепипед, ребра которого до приложения внешних сил имели размеры , и были параллельны координатным осям X, Y, Z.

Поставим задачу: Определить изменение объема, выделенного элемента, если стержень испытывает чистое центральное растяжение.

В соответствии с условием задачи только по граням параллелепипеда, перпендикулярным оси Х, действуют равномерно распределённые нормальные напряжения . Покажем их приложенными только в центре тяжести граней. Т.к. угловые деформации при центральном растяжении отсутствуют, то и в деформированном состоянии выделенный элемент остается прямоугольным параллелепипедом. Только его ребра получат приращения . Объем элемента до деформирования , после деформирования

Пренебрегая произведениями (подчеркнуты), как величинами большего порядка малости по сравнению с и 1,получим

Абсолютное изменение объема найдем из выражения

а относительное изменение объема вычислим по формуле

(8)

При подстановке в (8) вместо значений их соответствии с (6) после преобразований будем иметь

(9)

Если бы по граням выделанного элемента действовали равномерно распределенные напряжения то применяя принцип суперпозиции получим:

от действия только ---

от действия только --

От совместного действия

(10)

(11) - Обобщенный закон Гука.

Выражения (11) носят название обобщенного закона Гука.

Из (10) следует, что для изотропных материалов коэффициент Пуассона не может быть больше 0,5. Действительно, пусть , а (всестороннее растяжение). Тогда -происходить уменьшение объема тела при всестороннем растяжении элемента. Это противоречит результатам опыта и здравому смыслу, следовательно . Коэф. Пуассона, не может быть меньше нуля. Пусть происходить центральное растяжение стержня при , тогда тоже больше нуля, а и .

Т.о. для реальных изотропных материалов

е) Потенциальная энергия деформации при центральном растяжении (сжатии)

стержня из материала подчиняющегося закону Гука.

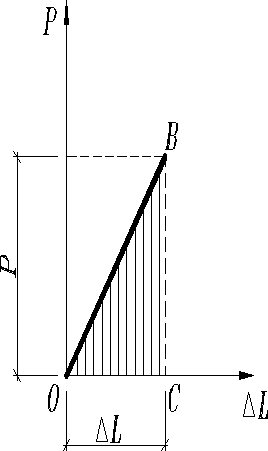
При центральном растяжении (сжатии) внешние силы совершают работу вследствие перемещения точек из приложения. Работа А статически приложенной внешней силы, возрастающей от 0 до значения Р с весьма небольшой скоростью (статическое нагружение) выражается (с учетом масштабов) заштрихованной площадью ОВС диаграммы , и следовательно, равна (12)

или с учетом (3’)

(12’).

При деформации стержня совершают работу и внутренние силы упругости. Т.к. они при нагружении всегда направлены в сторону противоположную перемещению, то работа внутренних сил при нагружении всегда отрицательная. При статическом нагружении и упругих деформациях величина, равная работе внутренних сил, но имеющая противоположный знак, называется потенциальной энергией деформации . Она представляет энергию, накопленную телом при деформации

(h)

На основании закона сохранения энергии имеем

или (13)

и, следовательно, при центральном растяжении (f).

В случае динамического нагружения и при появлении пластических деформаций, часть энергии внешних сил преобразуется в кинетическую движения, в электромагнитную, тепловую и т.д. Поэтому (f) использовать нельзя.

Подставив Р или из (3) в выражение (f), получим для определения потенциальной энергии при центральном растяжении постоянного сечения следующую формулу

(14)

Потенциальная энергия деформации, отнесенная к единице объема материала, называется удельной потенциальной энергией деформации

(15)

Пользуясь законом сохранения энергии (13) можно, при известной потенциальной энергии деформации , определить перемещение по направлению внешней силы, приложенной к системе. Широкое применение в расчетах конструкций имеет также принцип наименьшей работы, в соответствии с которым действительное напряженное состояние равновесия упругого тела (системы) отличается от всех смежных (возможных) состояний равновесия тем, что оно дает минимум потенциальной энергии деформации, т.е. (16)

Где - частная производная полной потенциальной энергии , являющейся функцией неизвестных величин, например, усилий в статически неопределенных стержневых системах, по неизвестному .

Т.о. условие (16) представляет исследователю нужное число линейных уравнений для определения неизвестных величин.

Замечание: при вычислении потенциальной энергии деформации принципом суперпозиции пользоваться нельзя, т.к. в выражение (14) сила Р входит во второй степени.

Центральное растяжение и сжатие