КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ТЕМА № 1 (2лц+2пр+4ср)
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Движением в широком смысле слова называется всякое изменение вообще.
Существуют: механическое, физическое, химическое, биологическое и социальное формы движения материи. Простейшей формой движения является механическое движение
Механическим движением называется изменение с течением времени положения тела в пространстве. Наглядность механических движений была причиной того, что из всех естественных наук механика раньше других получила широкое развитие.
Раздел физики, занимающийся изучением закономерностей механического движения и взаимодействия тел, называется механикой. В настоящее время механика подразделяется на:
1) классическую (неквантовую) механику;
2) квантовую механику.
В свою очередь классическая механика подразделяется:
1) ньютоновскую (нерелятивистскую) механику;
2) релятивистскую механику.
В основе ньютоновской механике лежат законы Ньютона. Эта механика справедлива лишь для макроскопических тел, движущихся со скоростями, малыми по сравнению со скоростью света. Под макроскопическим телом подразумевается тело, образованное очень большим числом атомов; масса такого тела во много раз превосходит массу отдельного атома.
Релятивистской называется механика, учитывающая требования специальной теории относительности (СТО). Она справедлива и при скоростях, сравнимых со скоростью света. Отметим, что согласно СТО скорости тел не могут быть больше скорости света.
Ни одна физическая задача не может быть решена абсолютно точно. Всегда получают приближенное решение. Степень приближения определяется характером задачи, целью, которую собираются достичь. Решая задачу приближенно, пренебрегают некоторыми факторами, которые в данный момент не существенны. Например, часто можно пренебречь размерами тела, движение которого изучается.
Тело, формой и размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.
Говоря о каком-то теле как о материальной точке, мы абстрагируемся от его размеров. Вторая абстракция, с которой приходится иметь дело в механике, это абсолютно твердое тело. В природе нет совершенно недеформируемых тел. Всякое тело под действием приложенных к нему сил в большей или меньшей степени деформируется, т.е. изменяет свою форму и размеры. Однако во многих случаях деформациями тел при рассмотрении их движений можно пренебречь. Если это имеет место, то тело называется абсолютно твердым. Таким образом, абсолютно твердым телом называется тело, деформациями которого в условиях данной задачи можно пренебречь.
Для однозначного определения положения исследуемого тела в произвольный момент времени необходимо выбрать систему отсчета. Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом, по отношению к которому определяется положение других тел в различные моменты времени.
Всякое движение твердого тела можно разложить на два основных вида движения поступательное и вращательное.
Поступательное движение это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе (рис. 1).
При вращательном движении все точки движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения (рис. 2а). Ось вращения может находиться и вне тела (рис. 2б).
Кинематика изучает движение тел, не интересуясь причинами, обусловливающими это движение. Динамика изучает движение тел в связи с теми причинами (взаимодействиями между телами), которые обусловливают тот или иной характер движения.
Радиус-вектор. Радиус-вектором некоторой точки называется вектор, проведенный из начала координат в данную точку (рис. 3).
Его проекции на координатные оси равны декартовым координатам данной точки:
, , . (1)
Радиус-вектор можно представить в виде
. (2)
Кроме того
. (3)
Из определения операции умножения вектора на скаляр следует, что всякий вектор можно представить в виде
, (4)
где модуль вектора , вектор с модулем равным единице, имеющий такое же направление, как и . Вектор называется единичным вектором или ортом вектора . Орт является безразмерной величиной.
2. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Материальная точка при своем движении описывает некоторую линию. Эта линия называется траекторией. В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение и т.д.
Пусть материальная точка (в дальнейшем для краткости мы будем называть ее частицей) переместилась вдоль некоторой траектории из точки 1 в точку 2 (рис. 4). Расстояние между точками 1 и 2, отсчитанное вдоль траектории, называется путем, пройденным частицей. Мы будем обозначать его буквой .
Прямолинейный отрезок, проведенный из точки 1 в точку 2, называется перемещением частицы. Обозначим его символом .
Предположим, что частица совершает последовательно два перемещения: и (см. рис. 5).
Суммой этих перемещений является такое перемещение , которое приводит к тому же результату, что и первые два перемещения вместе. Таким образом, перемещения характеризуются числовым значением и направлением, и кроме того, складываются по правилу параллелограмма. Отсюда следует, что перемещение есть вектор.
2.1. Скорость
Для характеристики направления и быстроты движения точки в механике вводится векторная физическая величина, называемая скоростью. Зафиксируем некоторый момент времени и рассмотрим приращение радиуса-вектора за малый промежуток времени , следующий за (рис. 6).
Средней скоростью точки в промежутке времени от до называется вектор , равный отношению приращения радиуса-вектора точки за этот промежуток времени к его продолжительности :
. (5)
Средняя скорость направлена так же, как и вектор перемещения , т.е. вдоль хорды, стягивающей соответствующий участок траектории точки.
Мгновенной скоростью точки в момент времени называется вектор , равный первой производной по времени от радиуса-вектора этой точки:
. (6)
Перемещение совпадает с бесконечно малым элементом траектории. Следовательно, мгновенная скорость направлена по касательной к траектории точки в сторону ее движения.
Найдем модуль скорости :
. (7)
В общем случае отрезок пути отличается от модуля перемещения . Однако если брать отрезки и , соответствующие все меньшим промежуткам времени , то различие между отрезками и будет убывать и их отношение в пределе станет равным единице:
. (8)
На этом основании можно заменить в формуле (7) на . В результате получим выражение
. (9)
Таким образом, модуль скорости равен производной пути по времени.
Вектор , как и всякий другой вектор, можно представить в виде
, (10)
где , , проекции вектора на координатные оси. Вместе с тем вектор равный выглядит следующим образом:
. (11)
Из сравнения выражений (10) и (11) вытекает, что
, , . (12)
Следовательно, проекция вектора скорости на координатную ось равна производной по времени соответствующей координаты движущейся частицы. Приняв во внимание (3), можно получить формулу
. (13)
Вектор скорости можно представить в виде
, (14)
где модуль скорости, а орт вектора . Введем орт касательной к траектории , условившись направлять его в ту же сторону, что и . Тогда очевидно, что орты и совпадут, так что можно написать следующее выражение:
. (15)
Получим еще одно выражение для скорости . С этой целью подставим в формулу (6) радиус-вектор в виде . Тогда
. (16)
Для простоты ограничимся случаем, когда траектория является плоской кривой, т.е. такой кривой, все точки которой лежат в одной плоскости. Примем эту плоскость за плоскость (рис. 7) .
В формуле (16) вектор оказался представленным в виде суммы двух составляющих. Первая составляющая, которую мы обозначим , равна
. (17)
Она направлена вдоль радиуса-вектора и характеризует быстроту изменения модуля вектора . Эта скорость называется радиальной скоростью. Вторая составляющая, которую мы обозначим , равна
. (18)
Эта составляющая характеризует быстроту изменения радиуса-вектора по направлению. Она называется трансверсальной скоростью.
Можно также показать, что
, (19)
где угол между радиусом-вектором и осью ( полярный угол, отсчитываемый от полярной оси ОХ в направлении против часовой стрелки, расстояние от полюса О до рассматриваемой точки), перпендикулярный к радиусу-вектору орт, направленный в сторону возрастания угла. Подставив это выражение для в (18), получим
. (20)
Мы ввели обозначения и , чтобы подчеркнуть, что составляющая и соответствующий орт связаны с изменением угла .
Очевидно, что векторы и взаимно перпендикулярны. Следовательно,
. (21)
2.2. Ускорение
При любом движении точки, кроме равномерного прямолинейного движения, скорость точки изменяется. Для характеристики быстроты изменения скорости точки в механике вводится векторная физическая величина, называемая ускорением.
Ускорением называется вектор , равный первой производной по времени от скорости этой точки:
. (22)
Заметим, что ускорение играет по отношению к такую же роль, какую вектор играет по отношению к радиусу-вектору .
На основании (6) ускорение точки равно также второй производной по времени от радиуса-вектора этой точки:
. (23)
Проекция вектора ускорения на координатную ось равна второй производной по времени соответствующей координаты движущейся частицы
, , . (24)
Подставим в формулу (22) выражение для скорости . Тогда получим
. (25)
Следовательно, вектор можно представить в виде суммы двух составляющих. Одна из них направлена по касательной к траектории и называется тангенциальным ускорением
. (26)
Вторая составляющая направлена по нормали к траектории и поэтому называется нормальным ускорением
. (27)
Модуль тангенциального ускорения равен
. (28)
Чтобы выяснить свойства нормального ускорения (27), нужно установить, чем определяется , т.е. быстрота изменения со временем направления касательной к траектории.
Очевидно, что эта быстрота будет тем больше, чем сильнее искривлена траектория и чем быстрее перемещается частица по траектории.
Степень искривленности плоской кривой характеризуется кривизной , которая определяется выражением
, (29)
где угол между касательными к кривой в точках, отстоящих друг от друга на (рис. 8).
Таким образом, кривизна определяет скорость поворота касательной при перемещении вдоль кривой.
Величина обратная кривизне , называется радиусом кривизны в данной точке кривой и обозначается буквой :
. (30)
Радиус кривизны представляет собой радиус окружности, которая сливается в данном месте с кривой на бесконечно малом ее участке. Центр такой окружности называется центром кривизны для данной точки кривой.
Можно показать, что
, (31)
где орт нормали к траектории, направленный в ту же сторону, в которую поворачивается вектор при движении частицы по траектории.
Величину можно связать с радиусом кривизны траектории и скоростью частицы . В результате несложных преобразований получается равенство
. (32)
Следовательно, быстрота поворота вектора скорости, как мы и предполагали, пропорциональна кривизне траектории и скорости перемещения частицы по траектории.
С учетом сказанного окончательная формула для нормального ускорения примет вид
. (33)
Модуль нормального ускорения равен
. (34)
Итак, вектор ускорения при движении частицы по плоской кривой определяется следующим выражением:
. (35)
Модуль вектора равен
. (36)
А2
А3
А1
В1
В2
В3
Рисунок 1
а)
б)
Рисунок 2
Рисунок 3
1
2
Траектория
r12
Рисунок 4
1
2
3
Рисунок 5
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 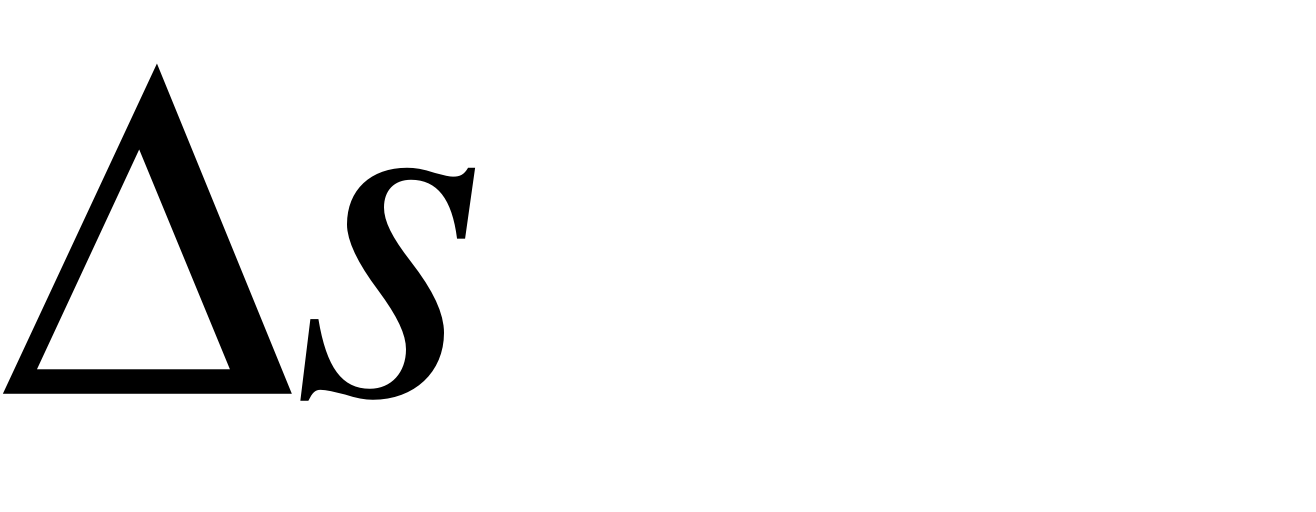
EMBED Equation.DSMT4 
Рисунок 6
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 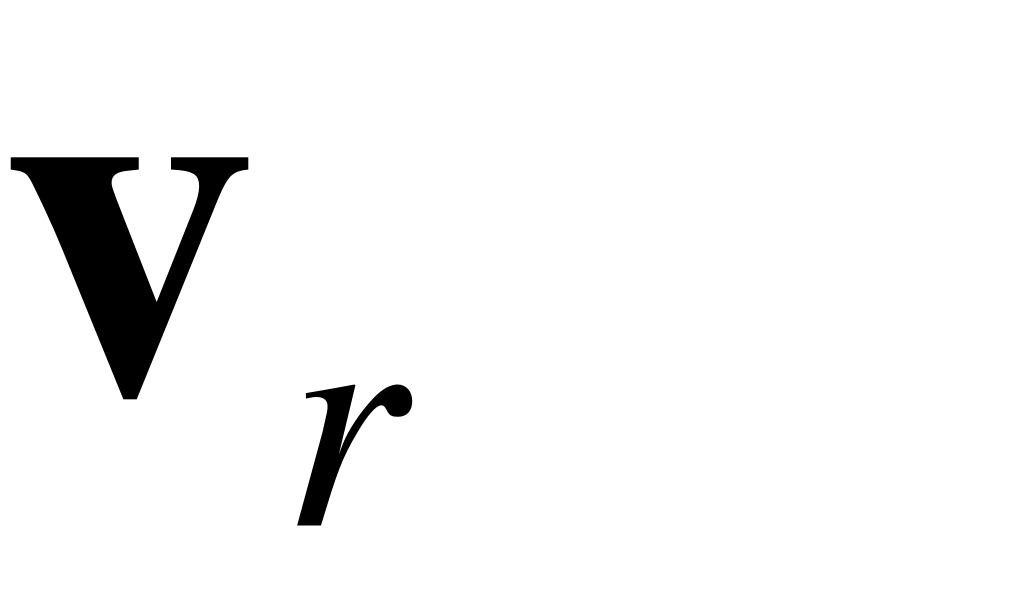
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 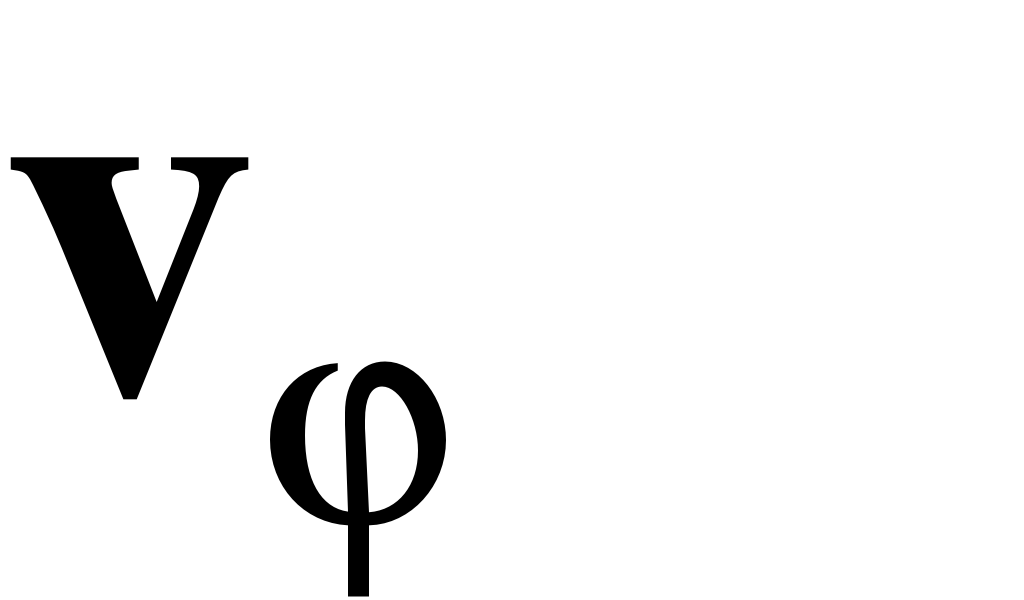
Рисунок 7
EMBED Equation.DSMT4 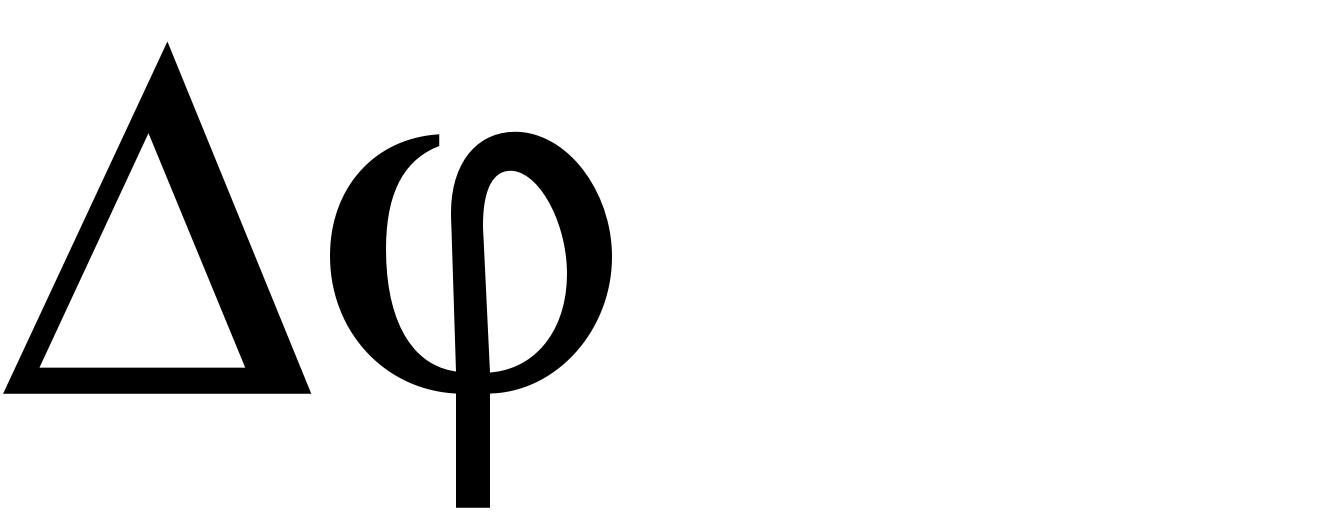
EMBED Equation.DSMT4 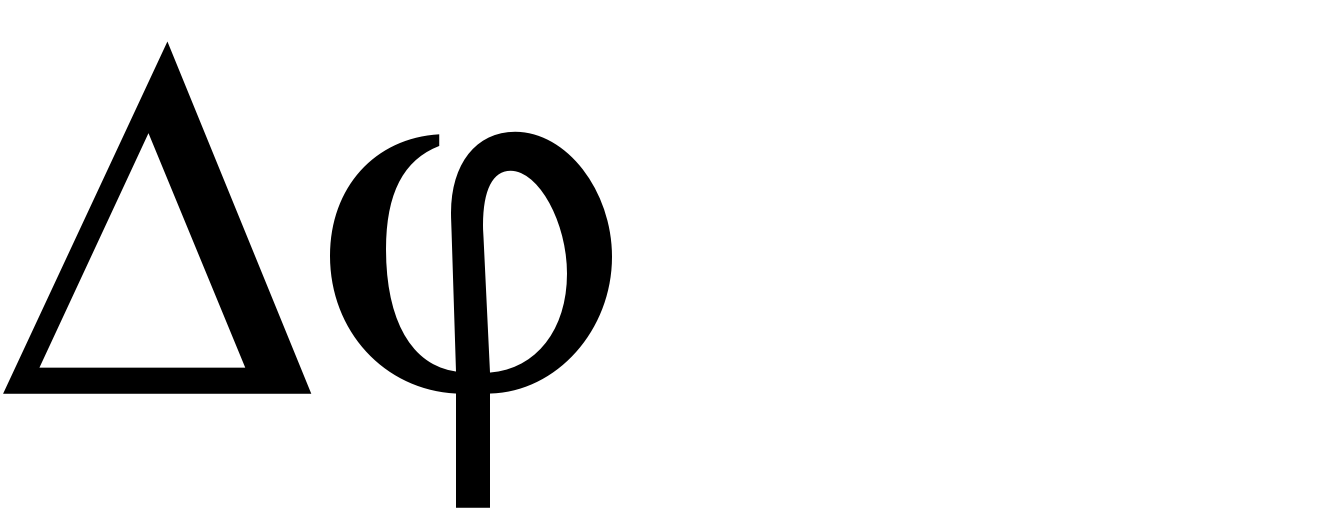
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 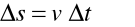
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
Рисунок 8
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ