Информатика, информационные технологии
1. Информатика, информационные технологии
1.1. Информация
1.1.1. Понятие информации
Термин информация используется во многих науках и во многих сферах человеческой деятельности. Он происходит от латинского слова «informatio», что означает «сведения, разъяснения, изложение».
Как известно, в материальном мире все физические объекты, окружающие нас, являются либо телами, либо полями. Физические объекты, взаимодействуя друг с другом, порождают сигналы различных типов. В общем случае любой сигнал – это изменяющийся во времени физический процесс. Такой процесс может содержать различные характеристики. Характеристика, которая используется для представления данных, называется параметром сигнала. Если параметр сигнала принимает ряд последовательных значений и их конечное число, то сигнал называется дискретным. Если параметр сигнала – непрерывная во времени функция, то сигнал называется непрерывным.
В свою очередь, сигналы могут порождать в физических телах изменения свойств. Это явление называется регистрацией сигналов. Сигналы, зарегистрированные на материальном носителе, называются данными. Существует большое количество физических методов регистрации сигналов на материальных носителях. Это могут быть механические воздействия, перемещения, изменения формы или магнитных, электрических, оптических параметров, химического состава, кристаллической структуры. В соответствии с методами регистрации, данные могут храниться и транспортироваться на различных носителях. Наиболее часто используемый и привычный носитель – бумага; сигналы регистрируются путем изменения ее оптических свойств. Сигналы могут быть зарегистрированы и путем изменения магнитных свойств полимерной ленты с нанесенным ферромагнитным покрытием, как это делается в магнитофонных записях, и путем изменения химических свойств в фотографии.
Данные несут информацию о событии, но не являются самой информацией, так как одни и те же данные могут восприниматься (отображаться или интерпретироваться) в сознании разных людей совершенно по-разному.
Чтобы получить информацию, имея данные, необходимо к ним применить методы, которые преобразуют данные в понятия, воспринимаемые человеческим сознанием. Методы, в свою очередь, тоже различны. Например, человек, знающий русский язык, применяет адекватный метод, читая русский текст. Соответственно, человек, не знающий русского языка и алфавита, применяет неадекватный метод, пытаясь понять русский текст. Таким образом, можно считать, что информация – это продукт взаимодействия данных и адекватных методов, т.е. это используемые данные.
Отсюда следует, что информация не является статическим объектом, она появляется и существует в момент слияния методов и данных, все прочее время она находится в форме данных. Момент слияния данных и методов называется информационным процессом (рис. 1.1).
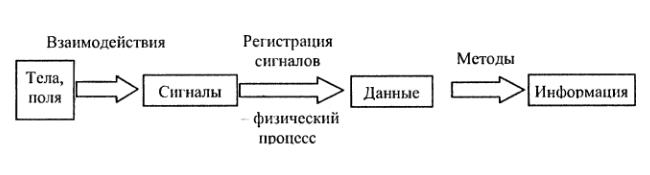
Рис. 1.1. Формирование информации
Человек воспринимает первичные данные различными органами чувств (их у нас пять – зрение, слух, осязание, обоняние, вкус), и на их основе сознанием могут быть построены вторичные абстрактные (смысловые, семантические) данные.
Таким образом, первичная информация может существовать в виде рисунков, фотографий, звуковых, вкусовых ощущений, запахов, а вторичная – в виде чисел, символов, текстов, чертежей, радиоволн, магнитных записей.
1.1.2. Свойства информации
Понятие «информация» используется многими научными дисциплинами, имеет большое количество разнообразных свойств, но каждая дисциплина обращает внимание на те свойства информации, которые ей наиболее важны. В рамках нашего рассмотрения наиболее важными являются такие свойства, как дуализм, полнота, достоверность, адекватность, доступность, актуальность. Рассмотрим их подробнее.
Дуализм информации характеризует ее двойственность. С одной стороны, информация объективна в силу объективности данных, с другой – субъективна, в силу субъективности применяемых методов. Например, два человека читают одну и ту же книгу и получают подчас весьма разную информацию. Более объективная информация применяет методы с меньшим субъективным элементом.
Полнота информации характеризует степень достаточности данных для принятия решения или создания новых данных на основе имеющихся. И неполный и избыточный наборы данных затрудняют получение информации и принятие адекватного решения.
Достоверность информации – это свойство, характеризующее степень соответствия информации реальному объекту с необходимой точностью. При работе с неполным набором данных достоверность информации может характеризоваться вероятностью, например, при бросании монеты выпадет герб с вероятностью 50 %.
Адекватность информации выражает степень соответствия создаваемого с помощью информации образа реальному объекту, процессу, явлению. Получение адекватной информации затрудняется при недоступности адекватных методов.
Доступность информации – это возможность получения информации при необходимости. Доступность складывается из двух составляющих: доступности данных и доступности методов. Отсутствие хотя бы одного дает неадекватную информацию.
Актуальность информации. Информация существует во времени, т. к. существуют во времени все информационные процессы. Информация, актуальная сегодня, может стать совершенно ненужной по истечении некоторого времени. Например, программа телепередач на нынешнюю неделю будет неактуальна для многих телезрителей на следующей неделе.
Атрибутивные свойства (атрибут – неотъемлемая часть чего-либо). Важнейшими среди них являются - дискретность (информация состоит из отдельных частей, знаков) и непрерывность (возможность накапливать информацию).
1.1.3. Количество информации
Во всякой информации присутствует субъективная компонента. А возможно ли вообще объективно измерить количество информации? Важнейшим результатом теории информации является вывод о том, что в определенных условиях, можно, пренебрегая качественными особенностями информации, выразить ее количество числом, а следовательно, сравнивать количество информации, содержащейся в различных группах данных.
Количеством информации называют числовую характеристику информации, отражающую ту степень неопределенности, которая исчезает после получения информации.
Понятия «информация», «неопределенность», «возможность выбора» тесно связаны. Получаемая информация уменьшает число возможных вариантов выбора (т.е. неопределенность), а полная информация не оставляет вариантов вообще.
Какое количество информации содержится, к примеру, в тексте романа «Война и мир», во фресках Рафаэля или в генетическом коде человека? Возможно ли объективно измерить количество информации?
В научном плане понятие «информация» связывается с вероят�ностью осуществления того или иного события.
Вероятность – числовая характеристика степени возможности наступления события. Вероятность достоверного события (обяза�тельно должно произойти) равна 1, невозможного события (не про�изойдет никогда) – 0. Вероятность случайного события лежит в ин�тервале (0, 1). Например, вероятность выпадения «орла» при под�брасывании монеты равна 1/2, а вероятность выпадения каждой из граней при игре в кости – 1/6.
Случайным называется событие, которое может произойти, а может и не произойти. Примерами случайных событий могут слу�жить выпадение «орла» при подбрасывании монеты или число оч�ков (т.е. выпадение определенной грани) при игре в кости.
Американский инженер Р. Хартли (1928) процесс получения ин�формации рассматривал как выбор одного сообщения из конечного заранее заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определяет как двоичный логарифм N.
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли I = log2N можно вычислить, какое количество информации для этого требуется: I = Iog2l00 = 6,644 бит, т.е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 бит.
Американский ученый Клод Шеннон предложил в 1948 г. другую формулу определения количества ин�формации, учитывающую возможную неодинаковую вероятность сообщений в наборе:
I = - (P1 log2 P1 + Р2 log2 Р2 + . . . + PN log2 PN),
где Pi – вероятность того, что именно i-e сообщение выделено в наборе из N сообщений.
Если вероятности P1, Р2, …, PN равны, то каждая из них равна 1/N, и формула Шеннона превращается в формулу Хартли.
Анализ формулы показывает, что чем выше вероятность собы�тия, тем меньшее количество информации возникает после его осу�ществления, и наоборот. Если вероятность равна 1 (событие досто�верно), количество информации равно 0.
Если вероятность свершения или несвершения какого-либо со�бытия одинакова, т.е. равна 1/2, то количество информации, кото�рое несет с собой это событие, равно 1. Это и есть единица измере�ния информации, которая получила наименование бит.
Бит можно также определить как количество информа�ции, которое содержит один разряд двоичного числа (отсюда назва�ние «бит»: binary digit – двоичный разряд). Бит в теории информа�ции – количество информации, необходимое для различения двух равновероятных сообщений.
Количество информации, равное 8 битам, называется байтом. В восьми разрядах можно записать 256 различных целых двоичных чисел от 00000000 до 11111111. Широко используются более крупные производные единицы информации:
1 Килобайт (Кбайт) = 1024 байт;
1 Мегабайт (Мбайт) = 1024 Кбайт;
1 Гигабайт (Гбайт) = 1024 Мбайт.
1 Терабайт (Тбайт) = 1024 Гбайт;
1 Петабайт (Пбайт) = 1024 Тбайт.
1.1.4. Информационные процессы
Получение информации тесно связано с информационными процессами, поэтому имеет смысл рассмотреть отдельно их виды.
Сбор данных – это деятельность субъекта по накоплению данных с целью обеспечения достаточной полноты. Соединяясь с адекватными методами, данные рождают информацию, способную помочь в принятии решения. Например, интересуясь ценой товара, его потребительскими свойствами, мы собираем информацию для того, чтобы принять решение: покупать или не покупать его.
Передача данных – это процесс обмена данными. Предполагается, что существует источник информации, канал связи, приемник информации, и между ними приняты соглашения о порядке обмена данными, эти соглашения называются протоколами обмена. Например, в обычной беседе между двумя людьми негласно принимается соглашение, не перебивать друг друга во время разговора.
Хранение данных – это поддержание данных в форме, постоянно готовой к выдаче их потребителю. Одни и те же данные могут быть востребованы не однажды, поэтому разрабатывается способ их хранения (обычно на материальных носителях) и методы доступа к ним по запросу потребителя.
Обработка данных – это процесс преобразования информации от исходной ее формы до определенного результата. Сбор, накопление, хранение информации часто не являются конечной целью информационного процесса. Чаще всего первичные данные привлекаются для решения какой-либо проблемы, затем они преобразуются шаг за шагом в соответствии с алгоритмом решения задачи до получения выходных данных, которые после анализа пользователем предоставляют необходимую информацию.
1.2. Представление (кодирование) данных
1.2.1. Системы счисления
Существуют различные способы записи чисел. Совокупность приемов записи и наименования чисел называется системой счисления. Числа записываются с помощью символов. По количеству символов, используемых для записи числа, системы счисления подразделяются на позиционные и непозиционные. Если для записи числа используется бесконечное множество символов, то система счисления называется непозиционной. Примером непозиционной системы счисления может служить римская. Например, для записи числа один используется буква I, два и три выглядят как совокупности символов II, III, но для записи числа пять выбирается новый символ V, шесть – VI, десять – вводится символ X, сто – С, тысяча – М и т.д. Бесконечный ряд чисел потребует бесконечного числа символов для записи чисел. Кроме того, такой способ записи чисел приводит к очень сложным правилам арифметики.
Позиционные системы счисления для записи чисел используют ограниченный набор символов, называемых цифрами, и величина числа зависит не только от набора цифр, но и от того, в какой последовательности записаны цифры, т.е. от позиции, занимаемой цифрой, например, 125 и 215. Количество цифр, используемых для записи числа, называется основанием системы счисления, в дальнейшем его обозначим q.
В повседневной жизни мы пользуемся десятичной позиционной системой счисления, q = 10, т.е. используется 10 цифр. Используя конечное число цифр, можно записать любое сколь угодно большое число. Число в позиционной системе счисления с основанием q может быть представлено в виде полинома по степеням q.
X(q) = xn-1qn-1 + xn-2qn-2 +…+ x1q1 + x0q 0 + x-1q -1 + x-2q -2 +… x-mq –m.
Здесь X(q) – запись числа в системе счисления с основанием q; хi – натуральные числа меньше q, т.е. цифры; n – число разрядов целой части; m – число разрядов дробной части.
Записывая слева направо цифры числа, мы получим закодированную запись числа в q-ичной системе счисления:
X(q) = xn-1 xn-2…x1 x0 x-1 x-2…x-m.
Основание системы записывается после числа в виде нижнего индекса. Например, одно и то же число 231, записанное в десятичной системе, запишется в двоичной, восьмеричной и шестнадцатеричной системах счисления следующим образом:
231(10)=11100111(2)=347(8)=E7(16).
Далее приведена табл. 1.4, содержащая наименования некоторых позиционных систем счисления и перечень знаков (цифр), из которых образуются в них числа.
Таблица 1.1. Некоторые системы счисления
|
Основание q
|
Система счисления
|
Знаки
|
|
2
|
Двоичная
|
0,1
|
|
8
|
Восьмеричная
|
0,1,2,3,4,5,6,7
|
|
10
|
Десятичная
|
0,1,2,3,4,5,6,7,8,9
|
|
16
|
Шестнадцатеричная
|
0,1,2,3,4,5,6,7,8,9,A.B,D,E,F
|
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, т. к. все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию q системы счисления.
|
0 + 0 = 0
|
0 0 = 0
|
|
0 + 1 = 1
|
0 1 = 0
|
|
1 + 0 = 1
|
1 0 = 0
|
|
1 + 1 = 10
|
1 1 = 1
|
В информатике, вследствие применения электронных средств вычислительной техники, большое значение имеет двоичная система счисления, q = 2. Таблица сложения и умножения двоичных чисел:
Преобразование из десятичной в прочие системы счисления проводится с помощью правил умножения и деления. При этом целая и дробная части переводятся отдельно.
Алгоритм перевода чисел из десятичной системы счисления в систему с основанием q > 1:
1) если переводится целая часть числа, то она делится на q, после чего запоминается остаток от деления. Полученное частное вновь делится на q, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на q выписываются в порядке, обратном их получению;
2) если переводится дробная часть числа, то она умножается на q, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на q и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая дробь в системе счисления с основанием q.
Рассмотрим алгоритм перевода десятичного числа 231 в двоичную систему (аналогично выполняется перевод из десятичной системы в любую q-ичную). Последовательное деление нацело позволяет разложить число по степеням двойки, а это в краткой записи и есть двоичное изображение числа.
231(10) = 1 27 + 1 26 + 1 25 + 0 24 + 0 23 + 1 22 + 1 21 +
+ 1 20 = 11100111(2).
Процесс деления записывают следующим образом:
231(10) = 11100111(2). 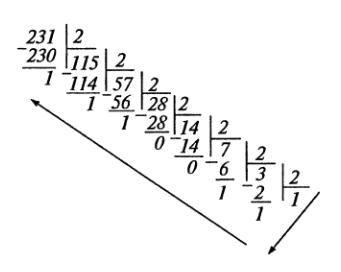
|
0
|
8125
2
|
|
1
|
625
2
|
|
1
|
250
2
|
|
0
|
5
2
|
|
1
|
0
|
Записывая значения частного и остатков от деления в виде нулей и единиц в порядке, обратном вычислению, получим двоичную запись числа.
Для дробных чисел правило последовательного деления заменяется правилом последовательного умножения. Рассмотрим на примере. Переведем 0,8125 из десятичной системы в двоичную систему счисления. Получаем таблицу:
Для выполнения арифметических операций в системе счисления с основанием q необходимо иметь соответствующие таблицы сложения и умножения.
Пример 1. Сложить числа:
а) 10000000100(2) + 111000010(2) = 10111000110(2);
б) 223,2(8) + 427,54(8) = 652,74(8); в) 3B3,6(16) + 38B,4(16) = 73E,A(16).
10000000100 223,2 3B3,6
+ 111000010 + 427,54 +38B,4
------------ ------- -----
10111000110 652,74 73E,A
Выполним проверку результатов расчетов переводом в десятичную систему счисления. Для этого переведем каждое слагаемое и сумму в десятичную систему счисления, выполним сложение слагаемых в десятичной системе счисления. Результат должен совпасть с суммой.
а) 10000000100(2)=1210+1 22 = 1024+4=1028(10)
111000010(2)=128+ 127+ 126+ 121 = 256+128+64+2 = 450(10)
10111000110(2) = 1210 + 128 + 127 + 126 + 122 + 121 = 1024 + 256 + 128 + 64 + 4 + 2 = 1478(10)
1028(10) + 450(10) = 1478(10)
Результаты совпадают, следовательно, вычисления в двоичной системе счисления выполнены верно! Примеры под буквами б) и в) проверьте самостоятельно.
Пример 2. Выполнить вычитание:
а) 1100000011,011(2) - 101010111,1(2) = 110101011,111(2);
б) 1510,2(8) - 1230,54(8) = 257,44(8); в) 27D,D8(16) - 191,2(16) = EC,B8(16).
1100000011,011 1510,2 27D,D8
- 101010111,1 -1230,54 -191,2
-------------- ------- ------
110101011,111 257,44 EC,B8
Пример 3. Выполнить умножение:
а) 100111(2) 1000111(2) = 101011010001(2).
б) 1170,64(8) 46,3(8) = 57334,134(8). в) 61,A(16) 40,D(16) = 18B7,52(16).
100111 1170,64 61,A
*1000111 * 46,3 *40,D
------------- -------------- ----------
100111 355 234 4F 52
+ 100111 + 7324 70 + 1868
100111 47432 0 ----------
100111 ------------- 18B7,52
------------- 57334,134
101011010001
Пример 4. Выполнить деление:
а) 100110010011000(2) : 101011(2)=111001000(2);
б) 46230(8) : 53(8)=710(8); в) 4C98(16) : 2B(16)=1C8(16).
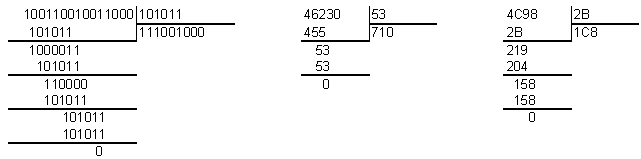
1.2.2. Представление данных в памяти компьютера
Представление чисел в компьютере.
Чтобы получить внутренне представление целого положительного числа N, хранящегося в k-разрядной ячейке памяти, необходимо
- Перевести число N в двоичную систему счисления
- Полученный результат дополнить слева незначащими нулями до k разрядов.
Например, 1910 = 100112 , значит, представление числа в памяти: 00010011.
Для кодирования целых чисел от 0 до 255 достаточно иметь 8 разрядов двоичного кода (8 бит). Шестнадцать бит позволяют закодировать целые числа от 0 до 65535, а 24 бита – уже более 16,5 миллионов разных значений.
Для хранения целых чисел со знаком отводится 2 ячейки памяти (16 бит), при этом старший (крайний левый) разряд отводится под знак числа. Если число положительное, то в этот разряд записывается 1, иначе – 0.
Представление положительных чисел с учетом знака называется прямым кодом числа. Для представления отрицательных чисел используется дополнительный код.
Получение дополнительного кода:
- Модуль числа (число без знака) записывают в прямом коде в n двоичных разрядах.
- Прямой код инвертируют ( заменяют 0 на 1 и наоборот) – получают обратный код
- К обратному коду +1.
Пример :
-1607
1. прямой код 1607 = 0000 0110 0100 0111
2. обратный код 1111 1001 1011 1000
3. +1 1111 1001 1011 1001
Для положительных чисел прямой, обратный и дополнительный коды совпадают.
Для кодирования действительных чисел используют 80-разрядное кодирование. При этом число предварительно преобразуется в нормализованную форму:
n = m * dp, где m – мантисса числа, р – порядок, d – основание системы счисления. Порядок указывает местоположение в числе точки. В зависимости от порядка точка передвигается (плавает) по мантиссе.
Первая часть числа называется мантиссой, а вторая – характеристикой. Большую часть из 80 бит отводят для хранения мантиссы (вместе со знаком) и некоторое фиксированное количество разрядов отводят для хранения характеристики (тоже со знаком).
Пример: Запишем код числа -312,3125
1. двоичная запись модуля числа имеет вид 100111000,0101
2. 100111000,1010=1,001110000101·28 (единицу в целой части отбросим)
3. Получаем смещенный порядок 8+1023=1031.
1031(10)=10000000111(2)
4. знак числа определит первый разряд. Получим
11000000011100111000010100…0 (после 1 сорок нулей))
Кодирование текстовых данных
Если каждому символу алфавита сопоставить определенное целое число (например, порядковый номер), то с помощью двоичного кода можно кодировать и текстовую информацию. Восьми двоичных разрядов достаточно для кодирования 256 различных символов.
В системе ASCII закреплены две таблицы кодирования – базовая(закрепляет значения кодов от 0 до 127) и расширенная ( от 128 до 255).
В России наиболее распространены следующие кодировки:
1. Windows-1251, используется на большинстве локальных компьютеров, работающих на платформе Windows.
2. КОИ-8 имеет широкое распространение в компьютерных сетях на территории России и в российском секторе Интернета.
3. ISO Международный стандарт, используется редко
4. Универсальная система кодирования текстовых данных UNICODE - система, основанная на 16-разрядном кодировании. Шестнадцать разрядов позволяют обеспечить уникальные коды для 65536 различных символов – этого поля достаточно для размещения в одной таблице символов большинства языков планеты.
3. Кодирование графических данных
1 байт – 256 цветов(28)
2 байта – 65538 цветов(216)
3 байта – 16,5 млн. цветов (224)
Графическое изображение состоит из мельчайших точек, образующих характерный узор, называемый растром. Так как линейные координаты и яркость каждой точки можно выразить с помощью целых чисел, то растровое кодирование позволяет использовать двоичный код для представления графических данных.
а) Черно-белые изображения - комбинации точек с 256 градациями серого цвета , 8-ми разрядное двоичное число.
б) Цветные графические изображения.
Способ разделения цветового оттенка на составляющие компоненты называется цветовой моделью.
В компьютерной графике наиболее распространены цветовые модели RGB, CMYK, HSB.
Цветовая модель RGB является аддитивной (основана на сложении цветов) и состоит из трех базовых цветов R (Red – красный), G (Green – зеленый) и B (Blue– синий). В данной модели действуют правила: G + B = C; G + R = Y; R + B = M
Характерная особенность аддитивного механизма заключается в том, что при взаимодействии лучей их суммарная яркость усиливается. Потому сложение трех достаточно интенсивных составляющих способно дать яркий белый цвет.
Цветовая модель CMYK является субтрактивной (основана на вычитании цвета из белого) и состоит из компонент голубой (С, Сyan), пурпурный (М, Magenta) и желтый( Y, Yellow). K – обозначает черный цвет.
Характерная особенность субтрактивного механизма заключается в том, что при взаимодействии нескольких цветных красителей итоговая яркость отраженного луча уменьшается. Соответственно, наложение на бумагу трех насыщенных красок способно дать в итоге черный цвет.
Цветовая модель HSB.
Наиболее удобна для человека, т.к. она хорошо согласуется с моделью восприятия цвета человеком. Компоненты модели HSB
- тон(Hue) – конкретный оттенок цвета
- насыщенность (Saturation) – интенсивность цвета (чистота)
- яркость (Brightness) – зависит от примеси черной краски, добавленной к данному цвету
Готовые изображения, предназначенные для демонстрации на экране, кодируют в модели RGB по 24-разрядной схеме. В этом случае на каждый канал цвета (из трех) приходится 8 бит, то есть один байт, например: 255, 255, 0 – желтый. Готовые изображения, предназначенные для печати на бумаге, кодируют в модели СМУК по 32-разрядной схеме (8 бит на канал цвета). В каждом из четырех цветовых каналов данные записываются одним байтом со значением от 0 до 100, например: 0, 0, 100, 0 – желтый.
1.3 Математические основы информатики
1.3.1. Алгебра высказываний (булева алгебра)
Основное понятие булевой алгебры – выказывание. Под простым высказыванием понимается повествовательное предложение, о котором можно сказать, истинно оно или ложно, поэтому высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (0) или ИСТИНА (1). Например, содержание высказывания А: «дважды два равно четырем» истинно А = 1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ. В дальнейшем нас не будет интересовать содержательная часть высказываний, а только их истинность. Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, записывается А = В.
Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций. Рассмотрим их подробней.
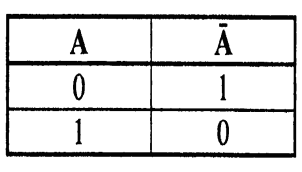
Операцией отрицания А (А, не А) называют высказывание А, которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то А - «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание – унарная (т.е. для одного операнда) логическая операция.
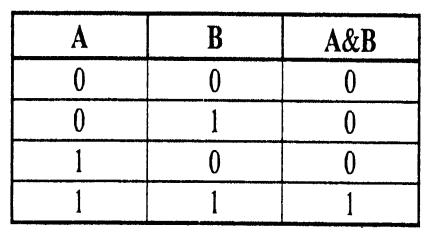
Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается С = А В или С = А & В (С равно А и В). Например, пусть высказывание А «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери».
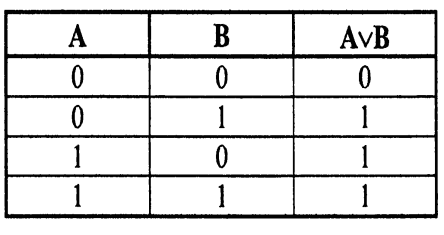
Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается С = A В (С равно А ИЛИ В). Пример: высказывание А «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе».
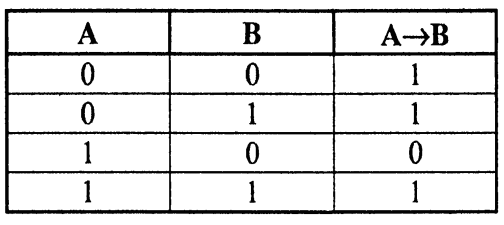
Импликацией двух высказываний А (А - посылка) и В (В - заключение) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается С = А В (из А следует В). Пример: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи». Операция не симметрична, т.е. из В А не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.
Эквиваленцией двух высказываний А и В является новое вы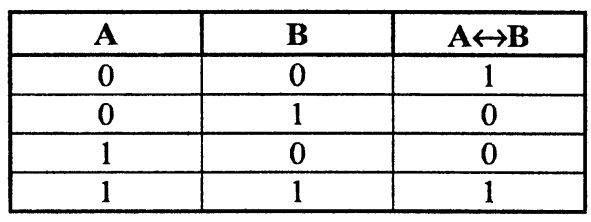
сказывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается С = А В (С = А В).
С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические
выражения, которые также называются булевскими функциями. Например, С = (( В) В) А. Чтобы избежать большого количества скобок в булевских функциях, принято соглашение о старшинстве операций. Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.
Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истинности следующие равносильности:
- = А
|
закон двойного отрицания
|
- А & В = В & А
|
коммутативный закон для конъюнкции
|
- A B = B A
|
коммутативный закон для дизъюнкции
|
- (А & В) & С = А & (В & С)
|
ассоциативный закон для конъюнкции
|
- (A B) C = A (B C)
|
ассоциативный закон для дизъюнкции
|
- А & (В С) = (А & В) (А & С)
|
дистрибутивные законы
|
- A (В & С) = (A В) & (A С)
|
|
-
|
законы де Моргана
|
-
|
|
- А & А = А
|
закон идемпотенции для конъюнкции
|
- A A = А
|
закон идемпотенции для дизъюнкции
|
- А & 1 = А
|
закон единицы для конъюнкции
|
- А & 0 = 0
|
закон нуля для конъюнкции
|
- A 1 = 1
|
закон единицы для дизъюнкции
|
- A 0 = А
|
закон нуля для дизъюнкции
|
- A = 1
|
закон исключения третьего
|
- А & = 0
|
закон противоречия
|
- А В = В
|
|
- А В = (А В) & (В А) = ( В) & (A ) = (A & B) ( & )
|
- A (А & В) = А
|
законы поглощения
|
- А & (A В) = А
|
|
- А & ( B) = A & B
|
|
- A (& В) = A В
|
|
Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь возможность приводить формулы с помощью эквивалентных преобразований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований.
Первая из них – дизъюнктивная нормальная форма (ДНФ), имеет вид Al A2 ... An, где каждое из составляющих высказываний есть конъюнкция простых высказываний и их отрицаний, например:
В = ( & А2 & A3) (А4 & А5).
Вторая – конъюнктивная нормальная форма (КНФ), имеет вид А1 А2 ... An, где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний, например:
В = .
1.4.2. Элементы теории множеств
Множеством называется любое объединение определенных вполне различимых объектов; их может и не быть вообще. Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединенные по любому признаку.
Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, оно обозначается . Множество, состоящее из конечного числа элементов, называется конечным, в противном случае – бесконечным. Задать множество можно перечислением его элементов. Например, множество образованное из n элементов а1, а2, ..., аn, обозначается А = {а1, а2, ..., ап}; пишется а А, если а является элементом множества А, в противном случае a A. Задать множество можно также, указав общее свойство для всех его и только его элементов.
Два множества считаются равными, если состоят из одних и тех же элементов; записывается этот факт А = В. Множество А1, называется подмножеством А, если все элементы множества А1 являются элементами А (записывается А1 А).
Для множеств определены следующие операции: объединение, пересечение, дополнение. Объединением множеств А и В (записывается AB) называется множество, состоящее из элементов как одного, так и второго множества. Пересечением множеств А и В (записывается АВ) называется множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно. Дополнением множества А до В называется множество, состоящее из элементов множества В, не принадлежащих А. Дополнение обозначается = В – А (рис. 1.7).
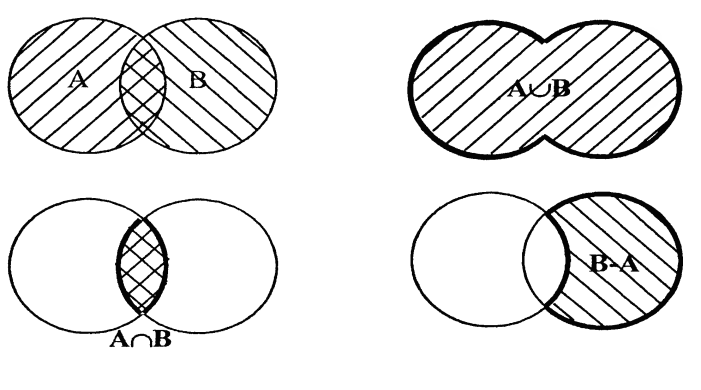
Рис. 1.2. Операции над множествами
4
_________________________Шадрина Н.Н., Шестакова О.Н., Яковлева Г.М.
PAGE \* MERGEFORMAT 21
Информатика, информационные технологии