Випадкові події та операції над ними
Лекція 2. Випадкові події та операції над ними.
План лекції
- Актуалізація опорних знань:
- Предмет теорії ймовірностей та математичної статистики.
- Логіка висловлювань, істинність висловлювань.
- Викладення нового матеріалу:
- Випадкові події;
- Операції над подіями.
- Контрольні питання:
- Що включає в собі поняття випробовування, дослід, експеримент?
- Випадкові події, достовірні, неможливі, протилежні, їх позначки;
- Повна група елементарних подій;
- Операції над подіями;
- Співвідношення, що є слідством з формул операцій над подіями.
- Приклади задач ща темою.
- Коментарі до самостійної роботи: Розв’язування задач з теми «Випадкові події та операції над ними».
Випадкові події
Забезпечення певного комплексу умов називають випробуванням або дослідом, а можливий результат випробування —подією. Наприклад, підкидання монети є випробуванням, а випадання «герба» або «номіналу» —подіями. Події позначатимемо великими латинськими літерами: А, В, C.
Подію називають випадковою, якщо вона може відбутися або не відбутися в даному випробуванні.
Достовірною називають подію, яка обов'язково відбудеться в даному випробуванні.
Неможливою називають подію, яка точно не відбудеться в даному випробуванні.
Зауважимо, що будь-яка подія пов'язана з певним випробуванням.
Дві події називають сумісними, якщо поява однієї з них не виключає появи іншої в одному й тому самому випробуванні.
Дві події називають несумісними, якщо вони не можуть відбутися одночасно в одному й тому самому випробуванні.
Попарно несумісні випадкові події А1,А2,...,Ап утворюють повну групу подій, якщо внаслідок випробування одна з них обов'язково відбудеться. Наприклад, події «виграш», «програш» і «нічия» (для певного гравця) утворюють повну групу подій у випробуванні —грі в шахи двох суперників.
Елементарними подіями (наслідками) у певному випробуванні називають усі можливі результати цього випробування, які не можна розкласти на простіші. Множину всіх можливих елементарних подій називають простором елементарних подій, який позначають . Наприклад, при підкиданні грального кубика простір елементарних подій утворюють події і = {випаде і очок}, і = 1, 2, 3, 4, 5, 6.
Елементарні події, при появі яких відбувається певна подія, називають сприятливими для цієї події. Наприклад, при підкиданні грального кубика для події А={випаде парне число очок} сприятливими є елементарні події 1, 3, 5.
Кожну подію можна розглядати як деяку підмножину простору елементарних подій у даному випробуванні. Зокрема, подія А = є достовірною, а подія В = —неможливою.
Приклад 1. Монету підкидають двічі. Для даного випробування описати простір елементарних подій.
Розв'язання. При двократному підкиданні монети можливі чотири елементарних наслідки: (А, А); (А, Р); (Р, А); (Р, Р),
де А —випадання аверса (зображення «герба»), Р —випадання реверса (зображення «номіналу»). Очевидно, вони утворюють повну групу подій, тому
= {(А, А); (А, Р);(Р, А); (Р, Р)}
є простір елементарних подій даного випробування.
Операції над подіями
Сумою двох випадкових подій А і В називають таку подію, яка полягає в появі хоча б однієї з подій А або В, і позначають А + В (або А В).
Сумою п випадкових подій А1,А2,...,Аn називають таку подію, яка полягає в появі принаймні однієї з цих подій (позначається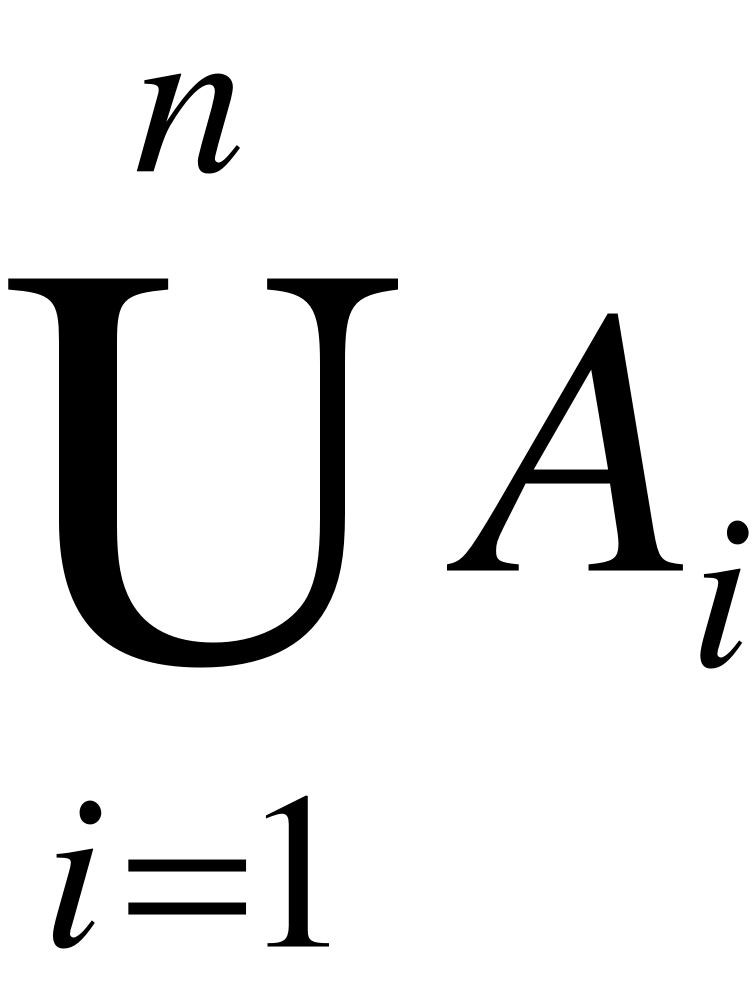 ).
).
Добутком двох випадкових подій А і В назівають таку подію, яка полягає в сумісній появі обох подій А і В, і позначають А •В (або А В).
Добутком п випадкових подій А1,А2,...,Ап називають таку подію, яка полягає в сумісній появі всіх цих подій (позначається 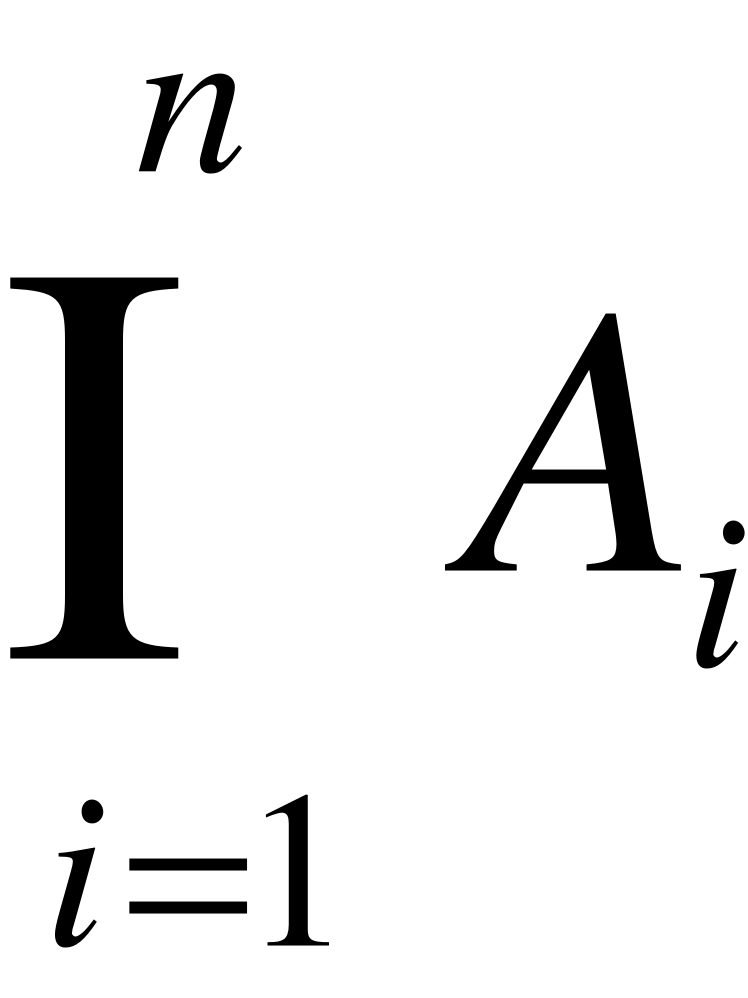 ).
).
Різницею двох випадкових подій А і В називають таку подію, яка полягає в виконанні події А і не виконанні події В, позначається як А –В, або А \ В.
Подію  називають протилежною до події А в даному випробуванні, якщо вона відбувається, якщо не відбувається подія А, тобто
називають протилежною до події А в даному випробуванні, якщо вона відбувається, якщо не відбувається подія А, тобто  = –А. Очевидно, протилежні події не сумісні і утворюють повну групу подій.
= –А. Очевидно, протилежні події не сумісні і утворюють повну групу подій.
Поняття суми і добутку подій можуть бути узагальнені на випадки будь-якого числа подій.
З визначення операцій додавання і множення слідують співвідношення:
1) A + А = A; A А = A ;
2) A + U = U; A U = A;
3) A+ = A ; A = ;
4) A + B = B + A ; A B = B A;
5) (A + B) + C = A + (B + C); (A B) C = A (B C);
6) A (B + C) = A B + A C.
Приклад 1. У ящику містяться кульки білого та чорного кольору. Навмання з нього виймають одну кульку. Подія А = {вийнято кульку білого кольору}, подія В = {вийнято кульку чорного кольору}. Сумісні чи несумісні ці події?
Розв’язання. Ці події несумісні, тому що поява події А виключає виконання події В, також події А і В утворюють повну групу події і є протилежні:  = В,
= В,  = А.
= А.
Приклад 2. Підкидають два гральних кубики. Нехай події Аі = {випаде і очок та першому кубику}, і = 1, 2, 3,4, 5, 6, Bj = {випаде і очок та другому кубику}, і = 1, 2, 3,4, 5, 6. Виразити через Аі,і Bj такі події:
а) сума очок на двох кубиках дорівнює п'яти;
б) випаде в сумі хоча б десять очок;
в) випаде в сумі не більше трьох очок.
Розв'язання.
а) Нехай С1= {сума очок на двох кубиках дорівнює п’яти}. Ця подія можлива тільки тоді, коли на першому кубику випаде і очок, а та другому j очок так, щоб і + j = 5, тобто і =1, j =4, або і = 2, j = 3, або і = 3, j = 2, або і = 4, j = 1. Отже,
С1= А1•В4 + А2 •В3 + А3 •В2 + А4 •В1.
б) Позначимо С2 = {випаде в сумі хоча б десять очок}. Подія С2 відбудеться тоді, коли на двох кубиках у сумі випаде або 10, або 11, або 12 очок, тобто і =4, j =6 або і =5, j =5 або і =6, j = 4 або і =6, j =5 або і =5, j =6 або і =6, j =6. Отже
С2= А4•В6 + А5 •В5 + А6 •В4 + А6 •В5. + А6 •В6. + А5 •В6.
в) Нехай Сз={випаде в сумі не більше трьох очок}. Оскільки найменша кількість очок, яка може випасти на кожному кубику, дорівнює одиниці, то подія Сз можлива лише тоді, коли сума очок на двох кубиках дорівнюватиме двом або трьом. Тому
Сз = А1 •В1 + А2 •В1 + А1 •В2..
Приклад 3. Два стрільці роблять постріл у мішень по одному разу. Позначимо події А = {у мішень влучив перший стрілець}, В = {у мішень влучив другий стрілець}. Виразити через А і В такі події: С = {два влучення в мішень} D = {жодного влучення в мішень} Е = {хоча б одне влучення в мішень} F = {лише одне влучення в мішень}.
Розв'язання. Простір елементарних подій складається з чотирьох подій
А •В,  •В, А •
•В, А • ,
,  •
• .
.
Подія С відбудеться тоді, коли обидва стрільці влучать с мішень. Тому вона є добутком двох подій А і В. Отже С = А •В
Подія D полягає в тому, що в мішень не влучить жодний стрілець, тобто не влучить ані перший ( ), ані другий (
), ані другий ( ). Тому D =.
). Тому D =. •
• .
.
Подія Е відбудеться тоді, коли влучить хоча б один стрілець. Це може бути толі, коли обидва стрільці влучать с мішень, або влучить перший, але не влучить другий, або не влучить перший, але влучить другий. Тоді
лець. Це може бути тоді, коли або обидва стрільці влучать у мішень, або перший влучить, другий не влучить, або перший не влучить, а другий влучить. Тому
Е = АВ +  В + А
В + А , тобто Е = А + В.
, тобто Е = А + В.
Подія F полягає в тому, що перший стрілець влучить в мішень, а другий не влучить, або другий влучить, а перший не влучить. Тому
F = В + А
В + А .
.
Приклади оформлення задач до розділу
Задача 1. Підкидають двічі гральний кубик. Нехай Аі = {випаде і очок при першому підкиданні} Ві = {випаде і очок при другому підкиданні } Виразити через Аі і Ві такі події:
А = {обидва рази випаде парна кількість очок},
В = {сума очок при двох підкиданнях дорівнює 6},
С = { сума очок при двох підкиданнях більше 8},
D = {обидва рази випаде однакова кількість очок}.
Відповідь. А =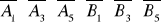 ;
;
В=А1В5+ А2В4+ А3В3+ А4В2+ А5В1;
С= А3В6+ А4В5+ А4В6+ А5В4+ А5В5+ А5В6+ А6В3+ А6В4+ А6В5+ А6В6;
D= А1В1+ А2В2+ А3В3+ А4В4+ А5В5+ А6В6;
Задача 2. Студент на екзамені відповідає на білет, у якому три питання. Нехай Аі = {студент відповів на і-те питання}. Виразити через Аі такі події:
А = {Студент відповів принаймні на два питання },
В = {Студент не відповів на жодне питання },
С = {студент відповів тільки на одне питання }.
Відповідь. А = 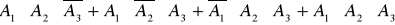 ; В=
; В=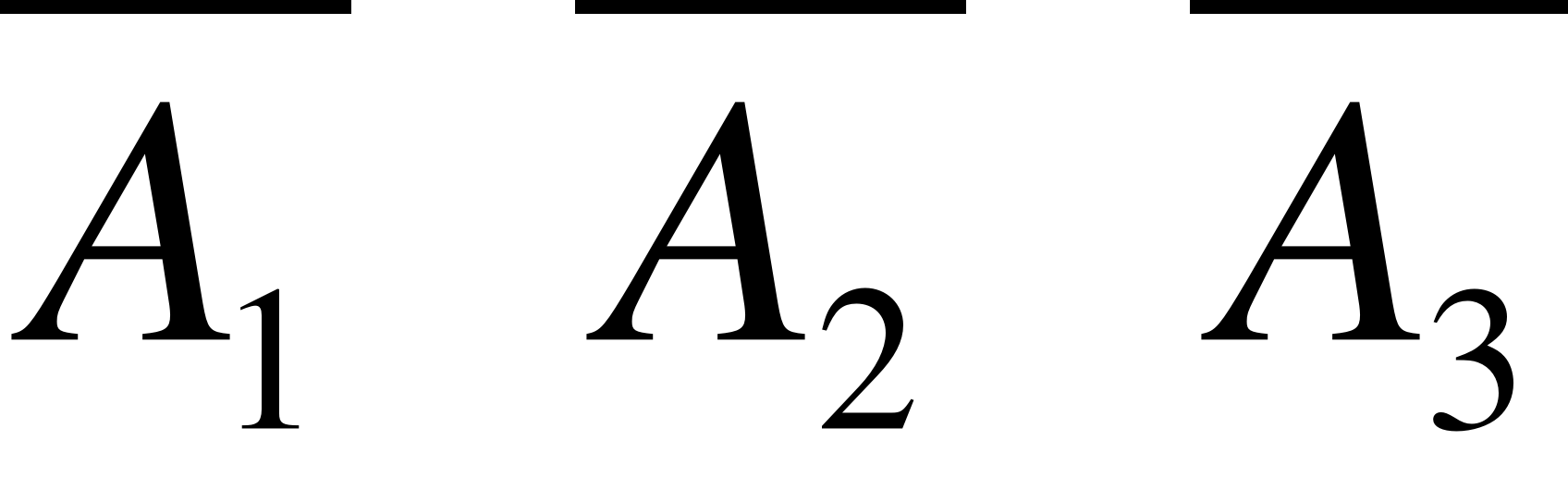 ;
;
С=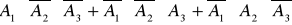 .
.
Задача 3. Підкидають три монети. Для даного випробування записати простір елементарних подій і розкласти на елементарні такі події:
А = {на двох монетах випаде «аверс»},
В = {на жодній монеті не випаде «реверс»},
С = {хоча б на одній монеті випаде «реверс»}.
Відповідь. = {(А, А, А); (А, А, Р); (А, Р, А); (А, Р, Р); (Р, А, А); (Р, А, Р);(Р, Р, А); (Р, Р, Р)}, А = {(А, А, Р); (А, Р, А); (Р, А, А)}; В = {(А, А, А)}; С = {(А, А, Р); (А, Р, А); (А, Р, Р); (Р, А, А); (Р, А, Р); (Р, Р, А); (Р, Р, Р)}.
Задача 4. Стрілець виконує чотири постріли в мішень. Нехай подія Аі = {влучення в мішень при і-му пострілі}. Виразити через Аі такі події:
А = {три влучення },
В = {хоча б один промах },
С = {не більше одного влучення },
D = {хоча б одне влучення}.
Відповідь. А = 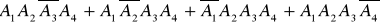 ; В =
; В =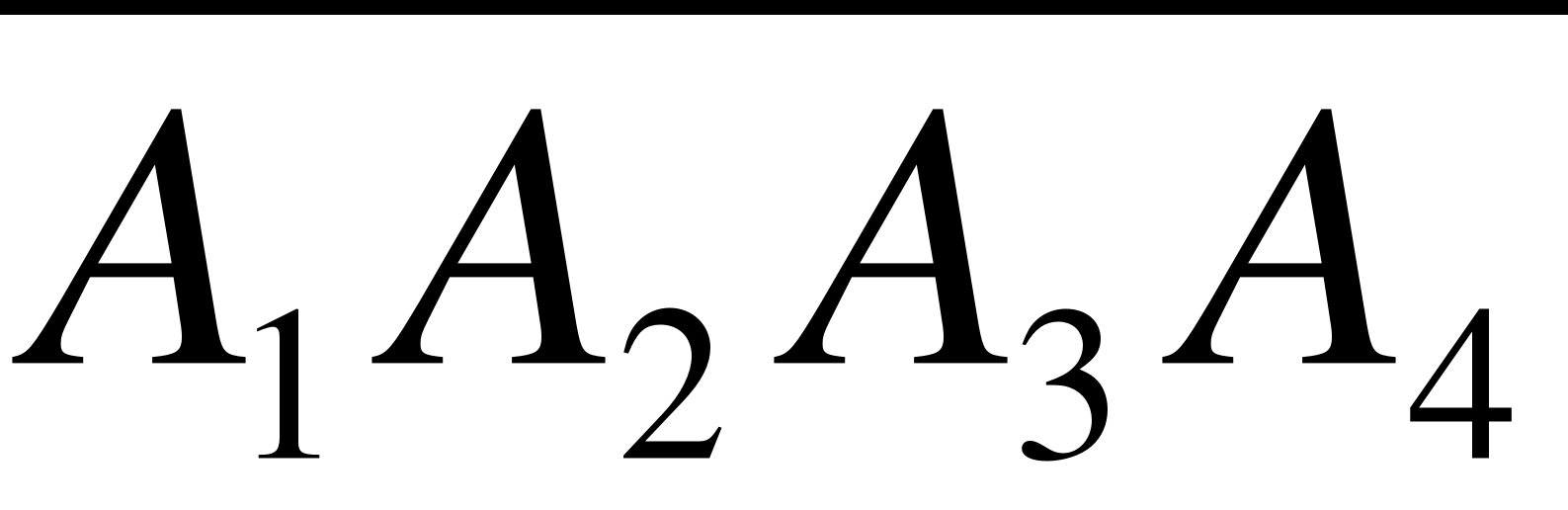 ;
;
С =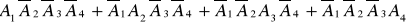 ; D =
; D =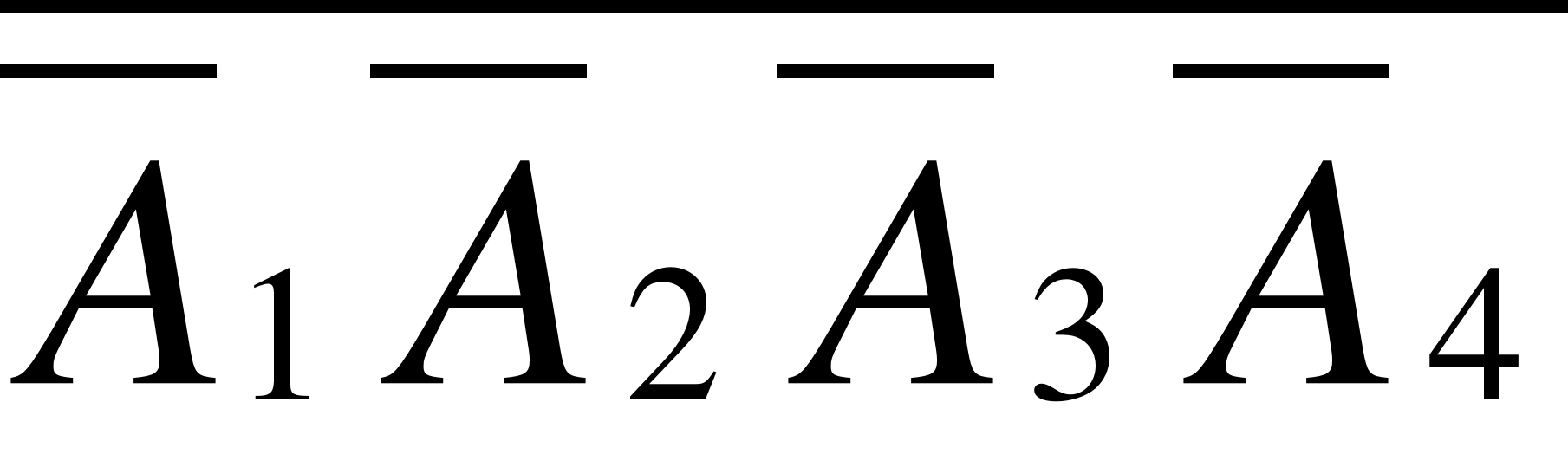 .
.
Задача 5. Підкидають чотири рази монету. Розкласти на елементарні такі події:
А = { на двох монетах випаде «аверс»}
В = {випаде не більше одного «реверса» }
Відповідь. А = {(А, А, Р, Р); (А, Р, А, Р); (А, Р, Р, А); (Р, А, А, Р); (Р, А, Р, А); (Р, Р, А, А)}, В = {(А, А, А, А); (А, А, А, Р);(А, А, Р, А); (А, Р, А, А);(Р, А, А, А)}.
Теорія ймовірностей та математична статистика
Випадкові події та операції над ними