СИСТЕМЫ НЕЧЕТКОГО ВЫВОДА

Лекция6. СИСТЕМЫ НЕЧЕТКОГО ВЫВОДА

Нечеткий вывод занимает центральное место в нечеткой логике и системах нечеткого управления. Процесс нечеткого вывода представляет собой некоторую процедуру или алгоритм получения нечетких заключений на основе нечетких условий или предпосылок с использованием рассмотренных выше понятий нечеткой логики. Этот процесс соединяет в себе все основные концепции теории нечетких множеств: функции принадлежности, лингвистические переменные, нечеткие логические операции, методы нечеткой импликации и нечеткой композиции.

Системы нечеткого вывода предназначены для реализации процесса нечеткого вывода и служат концептуальным базисом всей современной нечеткой логики. Системы нечеткого вывода позволяют решать задачи автоматического управления, классификации данных, распознавания образов, принятия решений, машинного обучения и многое другие.

Данная проблематика исследований тесно связана с целым рядом других научно-прикладных направлений, таких как: нечеткое моделирование, нечеткие экспертные системы, нечеткая ассоциативная память, нечеткие логические контроллеры, нечеткие регуляторы и просто нечеткие системы.

Базовая архитектура систем нечеткого вывода

Рассматриваемые в настоящей главе системы нечеткого вывода являются частным случаем продукционных нечетких систем или систем нечетких правил продукций, в которых условия и заключения отдельных правил формулируются в форме нечетких высказываний относительно значений тех или иных лингвистических переменных. Поскольку нечеткие лингвистические высказывания имеют фундаментальное значение в современной нечеткой логике, изучение систем нечеткого вывода начнем именно с них.

Нечеткие лингвистические высказывания

Нечетким лингвистическим высказыванием будем называть высказывания следующих видов.

1. Высказывание "b есть а", где b— наименование лингвистической переменной, а— ее значение, которому соответствует отдельный лингвистический терм из базового терм-множества Т лингвистической переменной b.

2. Высказывание "b есть Va", где V — модификатор, соответствующий таким словам, как: "ОЧЕНЬ", "БОЛЕЕ ИЛИ МЕНЕЕ", "МНОГО БОЛЬШЕ" и другим, которые могут быть получены с использованием процедур G и М данной лингвистической переменной.

3. Составные высказывания, образованные из высказываний видов 1 и 2 и нечетких логических операций в форме связок: "И", "ИЛИ", "ЕСЛИ-ТО", "НЕ".

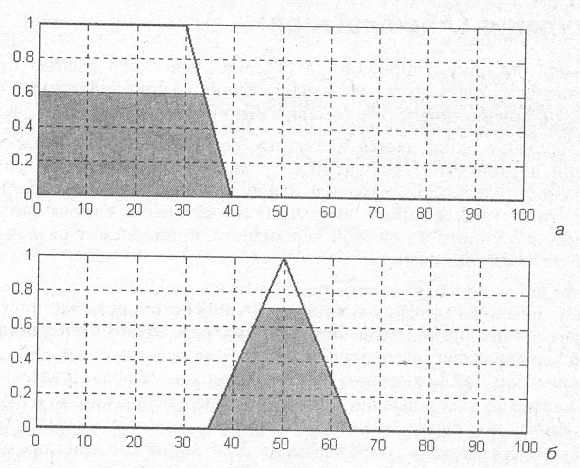
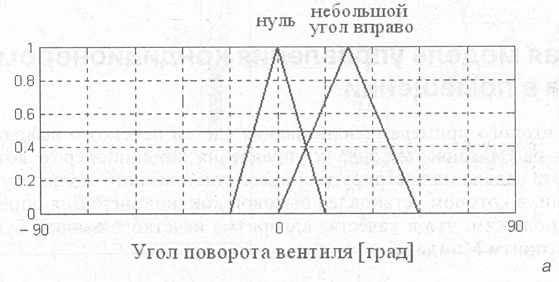
Пример. Рассмотрим некоторые примеры нечетких высказываний. Первое из них — "скорость автомобиля высокая" представляет собой нечеткое высказывание первого вида, в рамках которого лингвистической переменной "скорость автомобиля" присваивается значение "высокая". При этом предполагается, что на универсальном множестве Х переменной "скорость автомобиля" определен соответствующий лингвистический терм "высокая", который задается в форме функции принадлежности некоторого нечеткого множества (например, рис. 5.2).

Нечеткое высказывание второго вида "скорость автомобиля очень высокая" означает, что лингвистической переменной "скорость автомобиля" присваивается значение "высокая" с модификатором "ОЧЕНЬ", который изменяет значение соответствующего лингвистического терма "высокая" на основе использования некоторой расчетной формулы, например (3.47) для операции концентрации CON(A) нечеткого множества A для терма "высокая".

Нечеткое высказывание второго вида "скорость автомобиля более или менее высокая" означает, что лингвистической переменной "скорость автомобиля" присваивается значение "высокая" с модификатором "БОЛЕЕ ИЛИ МЕНЕЕ", который изменяет значение соответствующего лингвистического терма "высокая" на основе использования некоторой расчетной формулы, например (3.48) для операции растяжения DIL(A) нечеткого множества A для терма "высокая".

Ниже на рис. изображен пример функции принадлежности терм-множества "средняя" лингвистической переменной "скорость автомобиля" (а) и определение значений функций принадлежности этого же терм-множества для модификаторов "ОЧЕНЬ" (б) и "БОЛЕЕ МЕНЕЕ" (в).

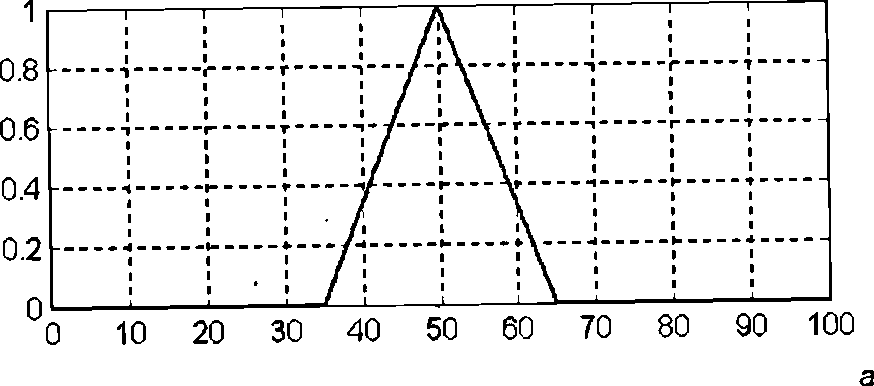
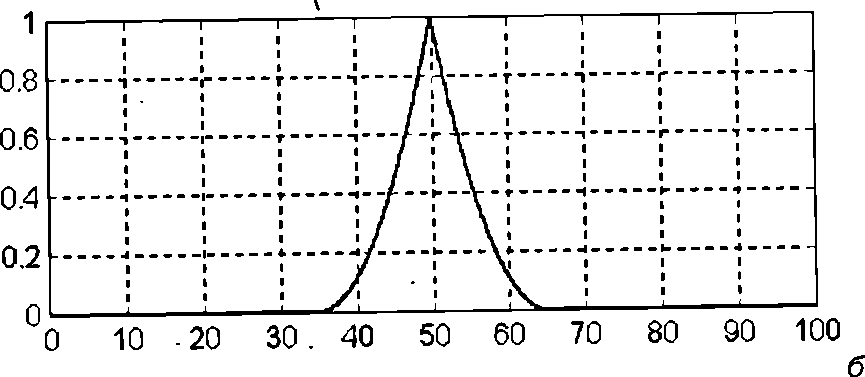
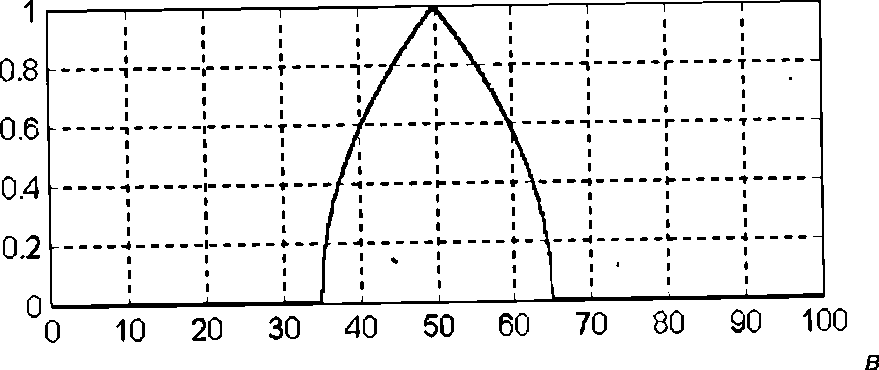
Наконец, нечеткое высказывание третьего вида "скорость автомобиля высокая и расстояние до перекрестка близкое" означает, что одной лингвистической переменной "скорость автомобиля" присваивается значение "высокая", а другой лингвистической переменной "расстояние до перекрестка" присваивается значение "близкое". Эти нечеткие высказывания первого вида соединены логической операцией нечеткая конъюнкция (операцией нечеткое "И").

Правила нечетких продукций в системах нечеткого вывода

Как уже отмечалось, рассматриваемые здесь системы нечеткого вывода являются частным случаем продукционных нечетких систем или систем нечетких правил продукций вида (6.21), определение которых было дано ранее. Основная особенность нечетких правил, используемых в системах нечеткого вывода, — условия и заключения отдельных нечетких правил формулируются в форме нечетких высказываний вида 1—3 относительно значений тех или иных лингвистических переменных.

Таким образом, всюду далее под правилом нечеткой продукции или просто — нечеткой продукцией будем понимать выражение следующего вида: (i) : Q; Р; А=>В, S, F, N, в котором все компоненты определены согласно (6.21), за исключением того, что условие ядра А и заключение ядра (консеквент) В представляют собой нечеткие лингвистические высказывания вида 1—3.

Простейший вариант правила нечеткой продукции, который наиболее часто используется в системах нечеткого вывода, может быть записан в форме:

ПРАВИЛО <#>: ЕСЛИ "b1 есть а'", ТО "b2 есть а"". (7.1)

Здесь нечеткое высказывание "b1 есть а"' представляет собой условие данного правила нечеткой продукции, а нечеткое высказывание "b2 есть а"" — нечеткое заключение данного правила. При этом считается, что b1=b2.

Система нечетких правил продукций.

Система нечетких правил продукций или продукционная нечеткая система представляет собой некоторое согласованное множество отдельных нечетких продукций или правил нечетких продукций в форме "ЕСЛИ А, ТО В" (или в виде: "IF А THEN В"), где А и В— нечеткие лингвистические высказывания вида 1, 2 или 3. Два последних случая нечетких высказываний требуют дополнительного пояснения.

Рассмотрим вариант использования в качестве условия или заключения в некотором правиле нечеткой продукции нечеткого высказывания вида 2. т. е. вида: "b есть Va", где V— модификатор, определяемый процедурами G и М лингвистической переменной b. Пусть терму a соответствует нечеткое множество A. В этом случае исходное нечеткое высказывание "b есть Va" можно преобразовать к виду 1 в форме нечеткого высказывание "b есть а'", где терм a' получается на основе применения определенной процедурами G и М операции к нечеткому множеству A. Полученное в результате подобной операции нечеткое множество A' принимается за значение терм-множества а'.

Если в качестве условия или заключения используются составные нечеткие высказывания, т. е. образованные из высказываний видов 1 и 2 и нечетких логических операций в форме связок: "И", "ИЛИ", "ЕСЛИ-ТО", "НЕ", то ситуация несколько усложняется. Поскольку вариант использования нечетких высказываний вида 2 сводится к нечетким высказываниям вида 1, то достаточно рассмотреть сложные высказывания, в которых нечеткими логическими операциями соединены только нечеткие высказывания вида 1.

Эта ситуация может соответствовать простейшему случаю, когда нечеткими логическими операциями соединены нечеткие высказывания, относящиеся к одной и той же лингвистической переменной, т. е. в форме: "b есть а'" ОП "р есть а"", где ОП — некоторая из бинарных операций нечеткой конъюнкции "И" или нечеткой дизъюнкции "ИЛИ".

Очевидно, в этом простейшем случае нечеткое высказывание "b есть а'" И "b есть а"" эквивалентно нечеткому высказыванию "b есть а*", где терм-множеству а* соответствует нечеткое множество A*, равное пересечению нечетких множеств A' и A", которые соответствуют термам a' и а". При этом операция пересечения определяется одним из ранее рассмотренных способов.

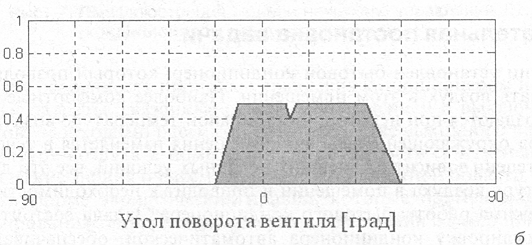
Пример. Рассмотрим составное нечеткое высказывание вида 3: "скорость автомобиля средняя и скорость автомобиля высокая". Ему соответствуют два нечетких высказывания первого вида, соединенные логической операцией нечеткой конъюнкции. Тогда исходное нечеткое высказывание эквивалентно нечеткому высказыванию первого вида: "скорость автомобиля средняя и высокая". Функция принадлежности терма "средняя и высокая" изображена на рис. б более темным фоном, при этом результат нечеткой конъюнкции определялся по формуле (3.3).

Рассмотрим аналогичное составное нечеткое высказывание вида 3: "скорость автомобиля средняя или скорость автомобиля высокая". Ему также соответствуют два нечетких высказывания первого вида, соединенные логической операцией нечеткой дизъюнкции. Тогда исходное нечеткое высказывание эквивалентно нечеткому высказыванию первого вида: "скорость автомобиля средняя или высокая". Функция принадлежности терма "средняя или высокая" изображена на рис. 2, в более темным фоном, при этом результат нечеткой дизъюнкции определялся по формуле (3.4).

Во-вторых, ситуация может соответствовать более сложному случаю, когда нечеткими логическими операциями соединены нечеткие высказывания, относящиеся к разным лингвистическим переменным в условии правила нечеткой продукции, т.е. в форме: "b1 есть а"' ОП "b2 есть a"", где ОП— некоторая из бинарных операций нечеткой конъюнкции "И" или нечеткой дизъюнкции "ИЛИ", a b1 и b2 —различные лингвистические переменные.

Этот вариант правил нечетких продукций может быть записан в следующей общей форме:

ПРАВИЛО <#>: ЕСЛИ "b1 есть а"' И "b2 есть а"" ТО "b3 есть v"

или

ПРАВИЛО <#>: ЕСЛИ "b1 есть а'" ИЛИ "b2 есть а"" ТО "b3 есть v".

Здесь нечеткие высказывания: "b1 есть a'" И "b2 есть a"", "b1 есть a"' ИЛИ "b2 есть а"" представляют собой условия правил нечетких продукций, а нечеткое высказывание "РЗ есть v" — заключение правил. При этом считается, что b1 b2 b3, а каждое из нечетких высказываний "b1 есть а"', "b2 есть а"" называют подусловиями данных правил нечетких продукций.

В случае правил нечетких продукций в форме (7.2) необходимо использовать один из методов агрегирования условий в левой части этих правил. Методы агрегирования рассматриваются ниже при описании этапа агрегирования.

Наконец, нечеткими логическими операциями могут быть соединены нечеткие высказывания, относящиеся к разным лингвистическим переменным в заключении правила нечеткой продукции, т. е. в форме: "b1 есть а'" ОП "b2 есть а"", где ОП— некоторая из бинарных операций нечеткой конъюнкции "И" или нечеткой дизъюнкции "ИЛИ", a b1 и b2—различные лингвистические переменные.

Этот вариант правил нечетких продукций может быть записан в следующей общей форме:

ПРАВИЛО <#>: ЕСЛИ "b1 есть a'" ТО "b2 есть а"" И "b3 есть v"

или

ПРАВИЛО <#>: ЕСЛИ "b1 есть а"' ТО "b2 есть а"" ИЛИ "b3 есть v".

Здесь нечеткое высказывание "b1 есть а'" представляет собой условие правил нечетких продукций, а нечеткие высказывания: "b2 есть а"" И "b3 есть v", "b2 есть a"" ИЛИ "b3 есть v" — заключения данных правил. При этом считается, что b1= b2= b3, а каждое из нечетких высказываний "b2 есть a"", "b3 есть v" называют подзаключениями данного правила нечеткой продукции.

Механизм или алгоритм вывода в системах нечеткого вывода

Механизм или алгоритм вывода является следующей важной частью базовой архитектуры систем нечеткого вывода. Применительно к системам нечеткого вывода механизм вывода представляет собой конкретизацию рассмотренных ранее методов прямого и обратного вывода заключений в системах нечетких продукций. В данном случае алгоритм вывода оперирует правилами нечетких продукций, в которых условия и заключения записаны в форме нечетких лингвистических переменных.

Для получения заключений в системах нечеткого вывода предложены несколько алгоритмов. Описание этих алгоритмов базируется на разделении процесса вывода на ряд последовательных этапов. Тем самым оказывается возможным не только достичь определенной систематизации понятий нечеткой логики, но и получить некоторую общую схему, которая позволяет формировать и другие алгоритмы нечеткого вывода.

Основные этапы нечеткого вывода

Говоря о нечеткой логике, чаще всего имеют в виду системы нечеткого вывода, которые широко используются для управления техническими устройствами и процессами. Разработка и применение систем нечеткого вывода включают в себя ряд этапов, реализация которых выполняется с помощью рассмотренных ранее основных положений нечеткой логики.

Информацией, которая поступает на вход системы нечеткого вывода, являются измеренные некоторым образом входные переменные. Эти переменные соответствуют реальным переменным процесса управления. Информация, которая формируется на выходе системы нечеткого вывода, соответствует выходным переменным, которыми являются управляющие переменные процесса управления.

Системы нечеткого вывода предназначены для преобразования значений входных переменных процесса управления в выходные переменные на основе использования нечетких правил продукций. Для этого системы нечеткого вывода должны содержать базу правил нечетких продукций и реализовывать нечеткий вывод заключений на основе посылок или условий, представленных в форме нечетких лингвистических высказываний.

Таким образом, основными этапами нечеткого вывода являются рис. 3):

Формирование базы правил систем нечеткого вывода.

Фаззификация входных переменных.

Агрегирование подусловий в нечетких правилах продукций.

Активизация или композиция подзаключений в нечетких правилах продукций.

Аккумулирование заключений нечетких правил продукций.

Ниже рассматриваются основные особенности каждого из этих этапов и приводятся простые примеры их выполнения.

Формирование базы правил систем нечеткого вывода

База правил систем нечеткого вывода предназначена для формального представления эмпирических знаний или знаний экспертов в той или иной проблемной области. В системах нечеткого вывода используются правила нечетких продукций, в которых условия и заключения сформулированы в терминах нечетких лингвистических высказываний рассмотренных выше видов. Совокупность таких правил будем далее называть базами правил нечетких продукций.

База правил нечетких продукций.

База правил нечетких продукций представляет собой конечное множество правил нечетких продукций, согласованных относительно используемых в них лингвистических переменных. Наиболее часто база правил представляется в форме структурированного текста:

ПРАВИЛО_1: ЕСЛИ "Условие_1" ТО "Заключение_1" (F1)

ПРАВИЛО_2: ЕСЛИ "Условие_2" ТО "3аключение_2" (F2) (7.4)

ПРАВИЛО_n: ЕСЛИ "Условие_n" ТО "Заключение_n" (Fn)

или в эквивалентной форме:

RULE_1: IF Condition_1 THEN Conclusion_1 (F1)

RULE_2: IF Condition_2 THEN Conclusion_2 (F2) (7.5)

RULE_n: IF Condition_n THEN Conclusion_n (Fn)

Здесь через F,(i {1, 2,..., n)) обозначены коэффициенты определенности или весовые коэффициенты соответствующих правил. Эти коэффициенты могут принимать значения из интервала [0, 1]. В случае, если эти весовые коэффициенты отсутствуют, удобно принять, что их значения равны 1.

Согласованность правил относительно используемых лингвистических переменных означает, что в качестве условий и заключений правил могут использоваться только нечеткие лингвистические высказывания вида (7.2) и (7.3), при этом в каждом из нечетких высказываний должны быть определены функции принадлежности значений терм-множества для каждой из лингвистических переменных.

Входные и выходные лингвистические переменные.

В системах нечеткого вывода лингвистические переменные, которые используются в нечетких высказываниях подусловий правил нечетких продукций, часто называют входными лингвистическими переменными, а переменные, которые используются в нечетких высказываниях подзаключений правил нечетких продукций, часто называют выходными лингвистическими переменными.

Таким образом, при задании или формировании базы правил нечетких продукций необходимо определить: множество правил нечетких продукций: P={R1, R2,..., Rn} в форме (7.5), множество входных лингвистических переменных: V={(b1, b2,..., bm} и множество выходных лингвистических переменных: W={(w1,w2,..., ws),}.

Тем самым база правил нечетких продукций считается заданной, если заданы множества Р, V, W.

Напомним, что входная bi V или выходная wj W лингвистическая переменная считается заданной или определенной, если для нее определено базовое терм множество с соответствующими функциями принадлежности каждого терма, а также две процедуры G и М. Наиболее распространенным случаем является использование в качестве функций принадлежности термов треугольных или трапециевидных функций принадлежности. При этом для удобства записи применяют специальные сокращения для наименования отдельных термов входных и выходных лингвистических переменных (табл. 1).

Таблица 1. Общепринятые сокращения для значений основных термов

лингвистических переменных в системах нечеткого вывода

Символическое Англоязычная нотация Русскоязычная нотация

обозначение

NB Negative Big Отрицательное большое

NM Negative Middle Отрицательное среднее

NS Negative Small Отрицательное малое

ZN Zero Negative Отрицательное близкое к нулю

Z Zero Нуль, близкое к нулю

ZP Zero Positive Положительное близкое к нулю

PS Positive Small Положительное малое

РМ Positive Middle Положительное среднее

РВ Positive Big Положительное большое

На формирование базы правил систем нечеткого вывода часто оказывают влияние некоторые дополнительные факторы, которые определяются спецификой решаемой задачи или используемого алгоритма нечеткого вывода.

Фаззификация (Fuzzification)

В контексте нечеткой логики под фаззификацией понимается не только отдельный этап выполнения нечеткого вывода, но и собственно процесс или процедура нахождения значений функций принадлежности нечетких множеств (термов) на основе обычных (не нечетких) исходных данных. Фаззификацию еще называют введением нечеткости.

Целью этапа фаззификации является установление соответствия между конкретным (обычно — численным) значением отдельной входной переменной системы нечеткого вывода и значением функции принадлежности соответствующего ей терма входной лингвистической переменной. После завершения этого этапа для всех входных переменных должны быть определены конкретные значения функций принадлежности по каждому из лингвистических термов, которые используются в подусловиях базы правил системы нечеткого вывода.

Формально процедура фаззификации выполняется следующим образом. До начала этого этапа предполагаются известными конкретные значения всех входных переменных системы нечеткого вывода, т.е. множество значений V={a1, a2,..., аm). В общем случае каждое аi из Х где X,— универсум лингвистической переменной bj. Эти значения могут быть получены либо от датчиков, либо некоторым другим, внешним по отношению к системе нечеткого вывода способом.

Далее рассматривается каждое из подусловий вида "bi, есть a'" правил системы нечеткого вывода, где a' — некоторый терм с известной функцией принадлежности m(х). При этом значение ai используется в качестве аргумента m(х), тем самым находится количественное значение bi’=m(ai). Это значение и является результатом фаззификации подусловия "bi есть a"'.

Этап фаззификации считается законченным, когда будут найдены все значения bi’=m(ai) для каждого из подусловий всех правил, входящих в рассматриваемую базу правил системы нечеткого вывода. Это множество значений обозначим через B={bi’}. При этом если некоторый терм а" лингвистической переменной bi не присутствует ни в одном из нечетких высказываний, то соответствующее ему значение функции принадлежности не находится в процессе фаззификации.

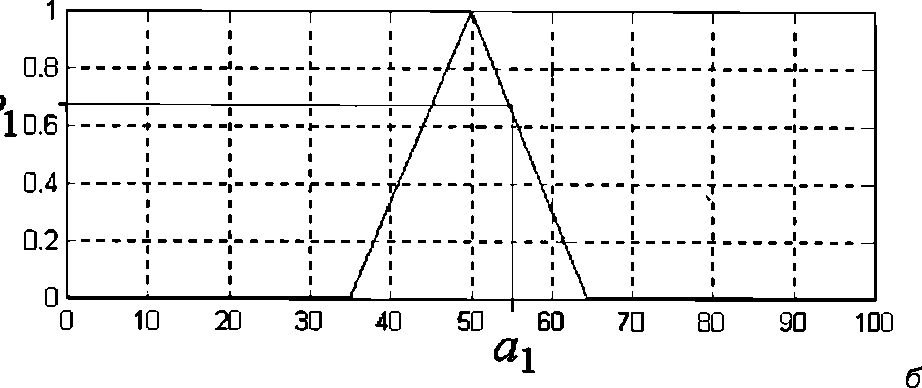
Пример. Для иллюстрации выполнения этого этапа рассмотрим пример процесса фаззификации трех нечетких высказываний: "скорость автомобиля малая", "скорость автомобиля средняя", "скорость автомобиля высокая" для входной лингвистической переменной bi — скорость движения автомобиля. Им соответствуют нечеткие высказывания первого вида: "b1 есть a1", "b1 есть a2", "b1 есть a3". Предположим, что текущая скорость автомобиля равна 55 км/ч, т. е. а1= 55 км/ч.

Тогда фаззификация первого нечеткого высказывания дает в результате число 0, которое означает его степень истинности и получается подстановкой значения a1= 55 км/ч в качестве аргумента функции принадлежности терма a1 (рис. 4, а). Фаззификация второго нечеткого высказывания дает в результате число 0.67 (приближенное значение), которое означает его степень истинности и получается подстановкой значения a1= 55 км/ч в качестве аргумента функции принадлежности терма a2 (рис. 4, б). Фаззификация третьего нечеткого высказывания дает в результате число 0, которое означает его степень истинности и получается подстановкой значения a1= 55 км/ч в качестве аргумента функции принадлежности терма a3 (рис.4, в).

Агрегирование (Aggregation)

Агрегирование представляет собой процедуру определения степени истинности условий по каждому из правил системы нечеткого вывода.

Формально процедура агрегирования выполняется следующим образом. До начала этого этапа предполагаются известными значения истинности всех подусловий системы нечеткого вывода, т. е. множество значений В={bi'}. Далее рассматривается каждое из условий правил системы нечеткого вывода. Если условие правила представляет собой нечеткое высказывание вида 1 или 2, то степень его истинности равна соответствующему значению bi'.

Если же условие состоит из нескольких подусловий вида (7.2), причем лингвистические переменные в подусловиях попарно не равны друг другу, то определяется степень истинности сложного высказывания на основе известных значений истинности подусловий. При этом для определения результата нечеткой конъюнкции или связки "И" может быть использована одна из формул (6.2)—(6.5), а для определения результата нечеткой дизъюнкции или связки "ИЛИ" может быть использована одна из формул (6.6)—(6.9). При этом значения bi' используются в качестве аргументов соответствующих логических операций. Тем самым находятся количественные значения истинности всех условий правил системы нечеткого вывода.

Этап агрегирования считается законченным, когда будут найдены все значения bk" для каждого из правил Rk,., входящих в рассматриваемую базу правил Р системы нечеткого вывода. Это множество значений обозначим через B"={b1", b2",..., bn’’}.

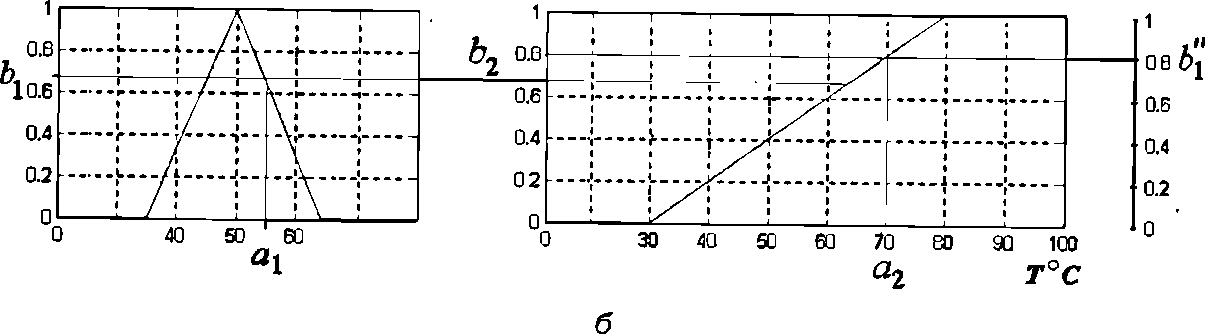
Пример. Для иллюстрации выполнения этого этапа рассмотрим пример процесса агрегирования двух нечетких высказываний: "скорость автомобиля средняя" И "кофе горячий" и "скорость автомобиля средняя" ИЛИ "кофе горячий" для входной лингвистической переменной bi — скорость движения автомобиля и b2—температура кофе. Предположим, что текущая скорость автомобиля равна 55 км/ч, т. е. а1= 55 км/ч, а температура кофе равна a2=70 °С.

Тогда агрегирование первого нечеткого высказывания с использованием операции нечеткой конъюнкции (6.2) дает в результате число b1"= 0.67 (приближенное значение), которое означает его степень истинности и получается как минимальное из значений 0.67 и 0.8 (рис.5, а). Агрегирование второго нечеткого высказывания с использованием операции нечеткой дизъюнкции (6.6) дает в результате число b1"= 0.8, которое означает его степень истинности и получается как максимальное из значений 0.67 и 0.8 (рис.5, б).

Активизация (Activation)

Активизация в системах нечеткого вывода представляет собой процедуру или процесс нахождения степени истинности каждого из подзаключений правил нечетких продукций. Активизация в общем случае во многом аналогична композиции нечетких отношений, но не тождественна ей. Поскольку в системах нечеткого вывода используются лингвистические переменные, то формулы (6.22)—(6.28) для нечеткой композиции теряют свое значение. В действительности при формировании базы правил системы нечеткого вывода задаются весовые коэффициенты Fi для каждого правила (по умолчанию предполагается, если весовой коэффициент не задан явно, то его значение равно 1).

Формально процедура активизации выполняется следующим образом. До начала этого этапа предполагаются известными значения истинности всех условий системы нечеткого вывода, т. е. множество значений В"={b1", b2"',..., bn"} и значения весовых коэффициентов Fi для каждого правила. Далее рассматривается каждое из заключений правил системы нечеткого вывода. Если заключение правила представляет собой нечеткое высказывание вида 1 или 2, то степень его истинности равна алгебраическому произведению соответствующего значения Ьi" на весовой коэффициент Fi.

Если же заключение состоит из нескольких подзаключений вида (7.3), причем лингвистические переменные в подзаключениях попарно не равны друг другу, то степень истинности каждого из подзаключений равна алгебраическому произведению соответствующего значения bi" на весовой коэффициент Fi. Таким образом, находятся все значения сk степеней истинности подзаключений для каждого из правил Rk, входящих в рассматриваемую базу правил Р системы нечеткого вывода. Это множество значений обозначим через C={ci, c2,..., cq}, где q— общее количество подзаключений в базе правил.

После нахождения множества С={ci, c2,..., cq} определяются функции принадлежности каждого из подзаключений для рассматриваемых выходных лингвистических переменных. Для этой цели можно использовать один из методов, являющихся модификацией того или иного метода нечеткой композиции:

О min-активизация:

m'(y)=min{ci,m(y)}, (7.6)

О prod-активизация:

m'(y)=ci..m(y), (7.7)

О average-активизация:

m'(y)=0.5.(ci+m(y)). (7.8)

где m(y) — функция принадлежности терма, который является значением некоторой выходной переменной wj, заданной на универсуме Y.

Этап активизации считается законченным, когда для каждой из выходных лингвистических переменных, входящих в отдельные подзаключения правил нечетких продукций, будут определены функции принадлежности нечетких множеств их значений, т. е. совокупность нечетких множеств: С1, C2,..., Сq, где q— общее количество подзаключений в базе правил системы нечеткого вывода.

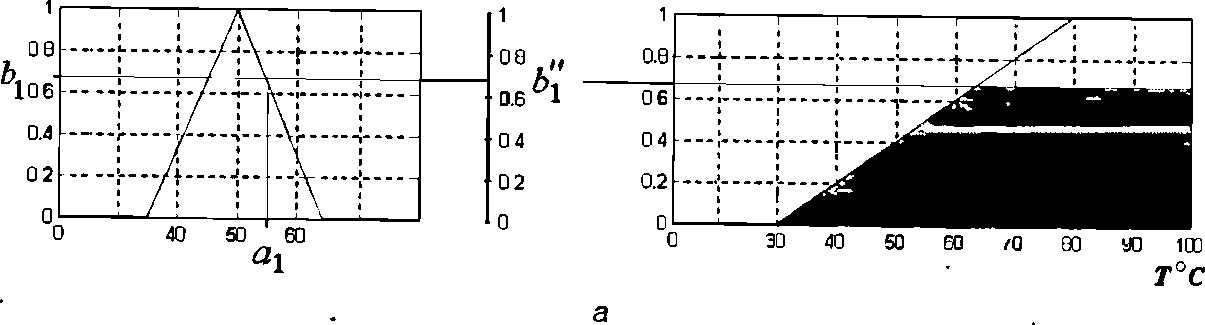
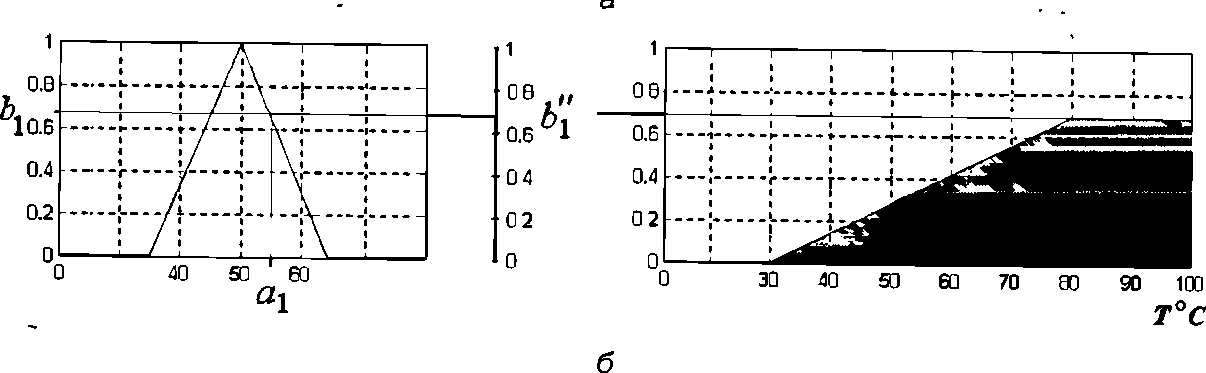
Пример. Для иллюстрации выполнения этого этапа рассмотрим пример процесса активизации заключения в следующем правиле нечеткой продукции (это правило вряд ли имеет целевое применение и используется формальным образом):

ЕСЛИ "скорость автомобиля средняя" ТО "кофе горячий"

Входной лингвистической переменной в этом правиле является b1 — скорость движения автомобиля, а выходной переменной является b2—температура кофе. Предположим, что текущая скорость автомобиля равна 55 км/ч, т. е. a1= 55 км/ч.

Поскольку агрегирование условия этого правила дает в результате b1"= 0.67, а весовой коэффициент равен 1 (по умолчанию), то значение 0.67 будет использоваться в качестве с1 для получения результата активизации. Результат, полученный методом min-активизации (7.6), изображен на рис. 6, а более темным цветом, а результат, полученный методом prod – активации- на рис b более темным цветом. В этом примере, в отличие от предыдущего, “температура кофе” – выходная лингвистическая переменная.

Аккумуляция (Accumulation)

Дефаззификация (Defuzzification)

Дефаззификация в системах нечеткого вывода представляет собой процедуру или процесс нахождения обычного (не нечеткого) значения для каждой из выходных лингвистических переменных множества W={w1, w2...., ws),}.

Цель дефаззификации заключается в том, чтобы, используя результаты аккумуляции всех выходных лингвистических переменных, получить обычное количественное значение (crisp value) каждой из выходных переменных, которое может быть использовано специальными устройствами, внешними по отношению к системе нечеткого вывода.

Действительно, применяемые в современных системах управления устройства и механизмы способны воспринимать традиционные команды в форме количественных значений соответствующих управляющих переменных. Именно по этой причине необходимо преобразовать нечеткие множества в некоторые конкретные значения переменных. Поэтому дефаззификацию называют также приведением к четкости.

Формально процедура дефаззификации выполняется следующим образом. До начала этого этапа предполагаются известными функции принадлежности всех выходных лингвистических переменных в форме нечетких множеств: С1', C2',...,Сs’, где s— общее количество выходных лингвистических переменных в базе правил системы нечеткого вывода. Далее последовательно рассматривается каждая из выходных лингвистических переменных wj W и относящееся к ней нечеткое множество Сj’. Результат дефаззификации для выходной лингвистической переменной wi, определяется в виде количественного значения yj R, получаемого по одной из рассматриваемых ниже формул.

Этап дефаззификации считается законченным, когда для каждой из выходных лингвистических переменных будут определены итоговые количественные значения в форме некоторого действительного числа, т. е. в виде y1,y2,...,ys, где s— общее количество выходных лингвистических переменных в базе правил системы нечеткого вывода.

Для выполнения численных расчетов на этапе дефаззификации могут быть использованы следующие формулы, получившие название методов дефаззификации.

Метод центра тяжести

Центр тяжести (CoG, COG, Centre of Gravity) или центроид площади рассчитывается по формуле:

В формуле используются следующие обозначения: у — результат дефаззификации; х— переменная, соответствующая выходной лингвистической переменной w; m(х)— функция принадлежности нечеткого множества, соответствующего выходной переменной w после этапа аккумуляции; Мin и Мах— левая и правая точки интервала носителя нечеткого множества рассматриваемой выходной переменной w.

При дефаззификации методом центра тяжести обычное (не нечеткое) значение выходной переменной равно абсциссе центра тяжести площади, ограниченной графиком кривой функции принадлежности соответствующей выходной переменной.

Пример дефаззификации методом центра тяжести функции принадлежности выходной лингвистической переменной "скорость движения автомобиля" изображен на рис. 8. В этом случае y1=40 км/ч (приближенное значение).

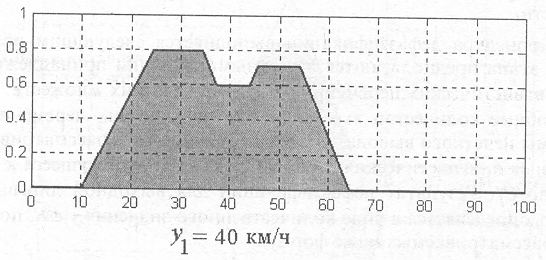Рис. 8

Алгоритмы нечеткого вывода:

Алгоритм Мамдани (Mamdani)

Алгоритм Мамдани является одним из первых, который нашел применение в системах нечеткого вывода. Он был предложен в 1975 г. английским математиком Е. Мамдани (Ebrahim Mamdani) в качестве метода для управления паровым двигателем. По своей сути этот алгоритм порождает рассмотренные выше этапы, поскольку в наибольшей степени соответствует их параметрам.

Формально алгоритм Мамдани может быть определен следующим образом.

- Формирование базы правил систем нечеткого вывода. Особенности формирования базы правил совпадают с рассмотренными выше при описании данного этапа.

- Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа.

- Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.

- Активизация подзаключений в нечетких правилах продукций. Осуществляется по формуле (7.6), при этом для сокращения времени вывода учитываются только активные правила нечетких продукций.

- Аккумуляция заключений нечетких правил продукций. Осуществляется по формуле (3.4) для объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным.

- Дефаззификация выходных переменных. Традиционно используется метод центра тяжести в форме (7.9)—(7.10) или метод центра площади.

Примеры использования систем нечеткого вывода в задачах управления

Одним из основных направлений практического использования систем нечеткого вывода является решение задач управления различными объектами или процессами. В этом случае построение нечеткой модели основывается на формальном представлении характеристик исследуемой системы в терминах лингвистических переменных. Поскольку кроме алгоритма управления, основными понятиями систем управления являются входные и выходные переменные, то именно они рассматриваются как лингвистические переменные при формировании базы правил в системах нечеткого вывода.

В общем случае цель управления заключается в том, чтобы на основе анализа текущего состояния объекта управления определить значения управляющих переменных, реализация которых позволяет обеспечить желаемое поведение или состояние объекта управления. В настоящее время для решения соответствующих задач используется общая теория управления, в рамках которой разработаны различные алгоритмы нахождения оптимальных законов управления объектами различной физической природы.

Не вдаваясь в детальное обсуждение концепций классической теории управления, рассмотрим лишь основные определения, необходимые для понимания особенностей и места систем нечеткого вывода при решении задач управления.

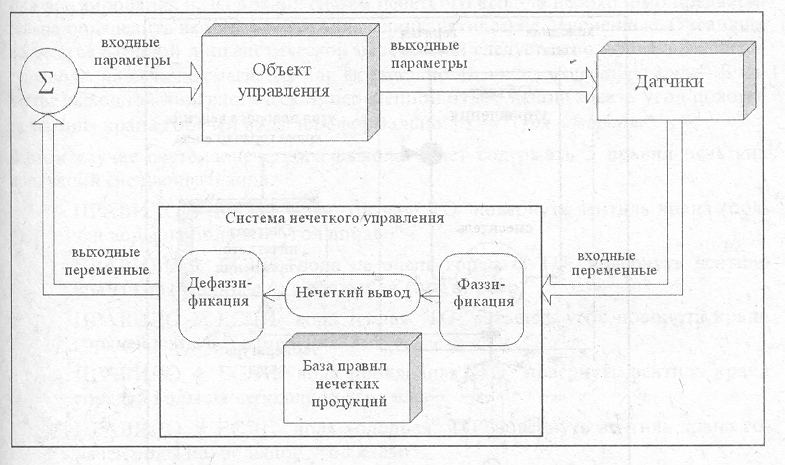
Базовая архитектура или модель классической теории управления основывается на представлении объекта и процесса управления в форме некоторых систем (рис.). При этом объект управления характеризуется некоторым конечным множеством входных параметров и конечным множеством выходных параметров. На вход системы управления поступают некоторые входные переменные, которые формируются с помощью конечного множества датчиков. На выходе системы управления с использованием некоторого алгоритма управления формируется множество значений выходных переменных, которые еще называют управляющими переменными или переменными процесса управления. Значения этих выходных переменных поступают на вход объекта управления и, комбинируясь со значениями входных параметров объекта управления, изменяют его поведение в желаемом направлении.

Рассмотренная архитектура называется процессом управления с обратной связью, а используемые для управления техническими объектами системы управления— контроллерами.

Наиболее типичным примером рассмотренной модели управления является так называемый интегрально-дифференцирующий контроллер или PID-контроллер (proportional-integral-derivative controller). Алгоритм его управления основан на сравнении выходных параметров объекта управления с некоторыми заданными параметрами и определении величины расхождения между ними или ошибки. После этого рассчитываются величины выходных переменных в форме аддитивной суммы величины этой ошибки, значения интеграла и производной по времени в течение некоторого промежутка времени.

Один из недостатков PID-контроллеров заключается в предположении о линейном характере зависимости входных и выходных переменных процесса управления, что существенно снижает адекватность этой модели при решении отдельных практических задач. Другой недостаток модели связан со сложностью выполнения соответствующих расчетов, что может привести к недопустимым задержкам в реализации управляющих воздействий при оперативном управлении объектами с высокой динамикой изменения выходных параметров.

Архитектура или модель нечеткого управления основана на замене классической системы управления системой нечеткого управления, в качестве которой используются системы нечеткого вывода. В этом случае модель нечеткого управления (рис.14) строится с учетом необходимости реализации всех этапов нечеткого вывода, а сам процесс вывода реализуется на основе одного из рассмотренных выше алгоритмов нечеткого вывода.

Далее рассматриваются особенности построения некоторых моделей систем нечеткого управления с целью решения практических задач по управлению конкретными объектами.

Нечеткая модель управления смесителем воды при принятии душа

В качестве первого примера использования систем нечеткого вывода в задачах управления рассматривается задача управления смесителем воды при принятии душа. Эта задача является одной из наиболее простых, которая может быть решена методами нечеткого моделирования. Для определенности предположим, что в качестве алгоритма нечеткого вывода будет использоваться алгоритм Мамдани.

Содержательная постановка задачи

При принятии душа на вход смесителя подается холодная и горячая вода по соответствующим магистральным трубопроводам. Наиболее комфортные условия для душа создаются при наличии на выходе смесителя теплой воды постоянной температуры. Поскольку во время принятия душа может наблюдаться неравномерный расход воды, температура воды на выходе смесителя будет колебаться, приводя к необходимости ручного изменения подачи холодной или горячей воды. Задача состоит в том, чтобы сделать регулировку температуры воды автоматической, обеспечивая постоянную температуру воды на выходе смесителя.

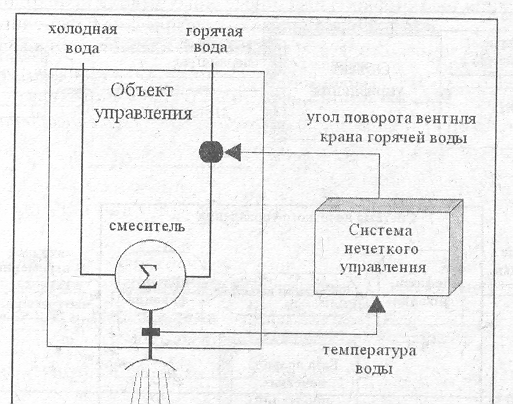
Опыт принятия душа позволяет сформулировать несколько эвристических правил, которые мы применяем в случае регулирования температуры воды на выходе смесителя:

1. Если вода горячая, то следует повернуть вентиль крана горячей воды на большой угол вправо.

2. Если вода не очень горячая, то следует повернуть вентиль крана горячей воды на небольшой угол вправо.

3. Если вода теплая, то оставить вентиль крана горячей воды без воздействия.

4. Если вода прохладная, то следует повернуть вентиль крана горячей воды на небольшой угол влево.

5. Если вода холодная, то следует повернуть вентиль крана горячей воды на большой угол влево.

Эта информация будет использоваться при построении базы правил системы нечеткого вывода, которая позволяет реализовать данную модель нечеткого управления.

Построение базы нечетких лингвистических правил

Для формирования базы правил систем нечеткого вывода необходимо предварительно определить входные и выходные лингвистические переменные. Очевидно, в качестве входной лингвистической переменной следует использовать температуру воды на выходе смесителя или формально: b1 — "температура воды". В качестве выходной лингвистической переменной будем использовать угол поворота вентиля крана горячей воды или формально: b2 — "угол поворота".

В этом случае система нечеткого вывода будет содержать 5 правил нечетких продукций следующего вида:

ПРАВИЛО_1: ЕСЛИ "вода горячая" ТО "повернуть вентиль крана горячей воды на большой угол вправо"

ПРАВИЛО_2: ЕСЛИ "вода не очень горячая" ТО "повернуть вентиль крана горячей воды на небольшой угол вправо"

ПРАВИЛО_3: ЕСЛИ "вода теплая" ТО "оставить угол поворота крана горячей воды без изменения"

ПРАВИЛО_4: ЕСЛИ "вода прохладная" ТО "повернуть вентиль крана горячей воды на небольшой угол влево"

ПРАВИЛО_5: ЕСЛИ "вода холодная" ТО "повернуть вентиль крана горячей воды на большой угол влево"

Фаззификация входных переменных

В качестве терм-множества первой лингвистической переменной будем использовать множество Т1 ={"горячая", "не очень горячая", "теплая", "прохладная", "холодная") с функциями принадлежности, изображенными на рис. 7.16, а.

В качестве терм-множества второй лингвистической переменной будем использовать множество Т2 = {"большой угол вправо", "небольшой угол вправо", "нуль"', "небольшой угол влево", "большой угол влево") с кусочно-линейными функциями принадлежности, изображенными на рис. 7.16, б. При этом температура воды измеряется в градусах Цельсия, а угол поворота— в угловых градусах. В последнем случае поворот вправо означает положительное направление отсчета, а поворот влево — отрицательное.

Используя в качестве алгоритма вывода алгоритм Мамдани, рассмотрим пример его выполнения для случая, когда текущая температура воды на выходе смесителя равна 55 °С. В этом случае фаззификация входной лингвистической переменной приводит к значениям степеней истинности 0.5 для правил нечетких продукций с номерами 2 и 3. Эти правила считаются активными и используются в текущем процессе нечеткого вывода.

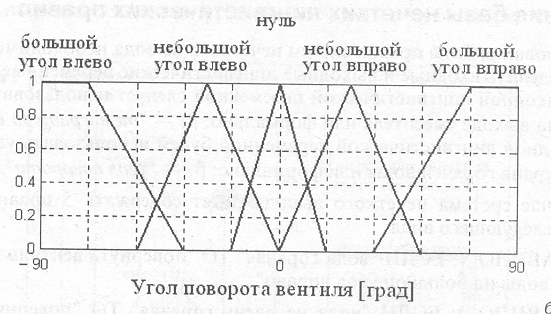
Поскольку все условия в правилах 1—5 заданы в форме нечетких лингвистических высказываний первого вида, этап их агрегирования тривиален и оставляет степени истинности 0.5 без изменения.

Следующим этапом нечеткого вывода является активизация заключений в нечетких правилах продукций. Поскольку все заключения правил 1—5 заданы в форме нечетких лингвистических высказываний первого вида, а весовые коэффициенты правил по умолчанию равны 1, то активизация правил 2 и 3 приводит к нечетким множествам, функции принадлежности которых изображены на рис. 7.17, а.

Аккумулирование заключений нечетких правил продукций с использованием операции max-дизъюнкции для правил 2 и 3 приводит в результате к нечеткому множеству, функция принадлежности которого изображена на рис. 7.17, б.

Дефаззификация выходной лингвистической переменной "Угол поворота венти.пя крана" методом центра тяжести для значений функции принадлежности, изображенной на рист7.17, приводит к значению управляющей переменной, равному повороту вентиля крана вправо на 16° (приближенное значение). Это значение и является результатом решения задачи нечеткого вывода для текущего значения входной лингвистической переменной "Температура воды".

Для реализации этого алгоритма нечеткого управления необходимо организовать периодическое измерение температуры воды на выходе смесителя в некоторые дискретные моменты времени. При этом, чем меньше интервал измерения этой температуры, тем выше оказывается точность регулирования температуры воды.

Что касается реализации собственно процедуры нечеткого управления, то для этой цели необходимо использовать соответствующие программные или аппаратные средства, специально предназначенные для выполнения всех этапов нечеткого вывода. В частности, для этой цели могут быть применены специальные программируемые нечеткие контроллеры, которые обладают возможностью реализовывать программу нечеткого вывода, записанную, например, на языке нечеткого управления или языка FCL.

Нечеткая модель управления контейнерным краном

Рассмотрим пример разработки модели системы нечеткого управления контейнерным краном, который предназначен для транспортировки моноблочных контейнеров при выполнении разгрузочных работ морских судов.

Содержательная постановка задачи

Контейнерные краны используются при выполнении погрузочло-разгрузочных работ в портах. Они соединяются с моноблочным контейнером гибким тросом и поднимают контейнер к кабине крана. Кабина крана вместе с контейнером может перемещается в горизонтальном направлении по направляющим типа рельсов. Когда контейнер поднимается к кабине, а кран приходит в движение, контейнер начинает раскачиваться и отклоняться от строго вертикального положения под кабиной крана.

Проблема заключается в том. что пока контейнер раскачивается в ходе своей транспортировки и отклоняется от вертикали, он не может быть опущен на железнодорожные платформы или другие транспортные средства.

Анализ действий крановщиков показывает, что они в своей работе применяют следующие эвристические правила:

Начинать движение следует со средней мощностью.
Если движение уже началось и кабина находится далеко от цели, отрегулировать мощность двигателя таким образом, чтобы контейнер оказался несколько впереди кабины крана.
Если кабина находится близко над целью, уменьшить скорость таким образом, чтобы контейнер находился несколько впереди кабины крана.
Когда контейнер находится очень близко от позиции цели, следует снизить мощность двигателя.
Когда контейнер находится прямо над позицией цели, следует остановить
двигатель.

Формирование базы правил систем нечеткого вывода