ТЕРТЯ У ГВИНТОВИХ КІНЕМАТИЧНИХ ПАРАХ

ЛЕКЦІЯ 24

ТЕРТЯ У ГВИНТОВИХ КІНЕМАТИЧНИХ ПАРАХ

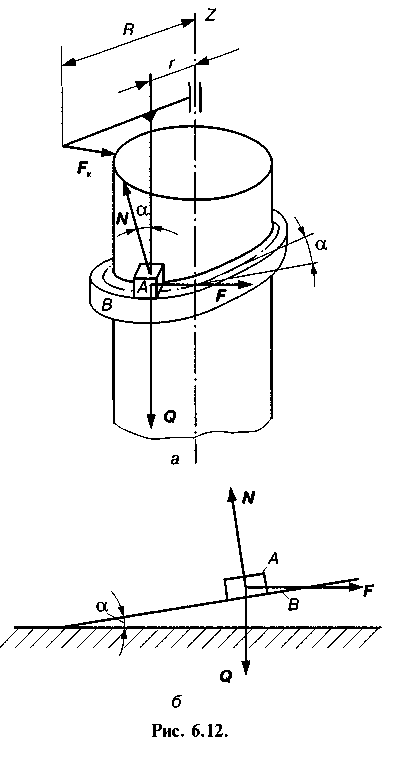
При розгляді тертя у гвинтових кінематичних парах, звичайно, роблять цілий ряд припущень. По-перше, оскільки закон розподілу тисків по гвинтовій нарізці невідомий, то умовно вважають, що тиск гайки на гвинт або, навпаки, гвинта на гайку прикладений по середній лінії нарізки, розміщеної на відстані г від осі гвинта (рис. 6.12, а). По-друге, припускають, що дію сил у гвинтовій парі можна звести до дії сил на повзун, який знаходиться на похилій площині (рис. 6.12, б), тобто, розгортаючи середню лінію гвинтової нарізки на площину, зводять просторову задачу до плоскої, для чого поступають так.

Нехай на гайку А, яку зображаємо у вигляді елементарного кубика, діє деяка осьова сила Q і деяка пара сил у площині, перпендикулярній до осі гвинта ж. Момент цієї пари можна вважати моментом сили FK, що прикладена на відстані R від осі

Для того щоб елемент гайки А рухався рівномірно вгору по гвинтовій поверхні, необхідно, щоб момент М дорівнював моменту сили F відносно цієї ж осі ж, тобто

В останньому рівнянні F є сила, яка необхідна для рівномірного переміщення тіла А (гайки) по похилій площині В, кут підйому б якої дорівнює кутові підйому гвинтової нарізки по середньому радіусу (див. рис. 6.12, б}. З рівнян ня (6.12) випливає, що сила F визначається за формулою

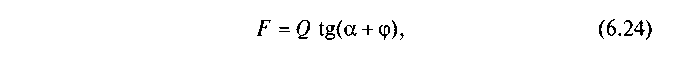
отже, з урахуванням (6.23) і (6.24) маємо

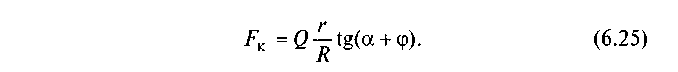
У випадку руху гайки А у напрямку, що збігається з напрямком сили Q (рух вниз), формула (6.25) набуває вигляду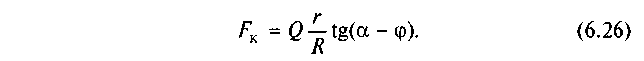

При б < ц в гвинтовій парі буде самогальмування. ККД гвинтової пари визначається, як і для похилої площини, формулами (6.14), (6.15).

Виведеними формулами можна користуватися при дослідженні гвинтових пар з прямокутною нарізкою. Якщо нарізка трикутна або трапецоїдна, то таку кінематичну пару можна розглядати як похилу площину з клиновим повзуном (рис. 6.13), в якого кут між вертикаллю і стінками жолоба дорівнює 90° — в, де кут 2в — кут профілю різьби. Тоді зведений коефіцієнт тертя/'на

основі (6.20) матиме вираз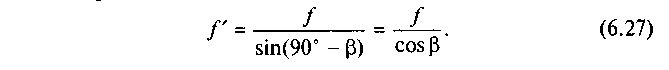

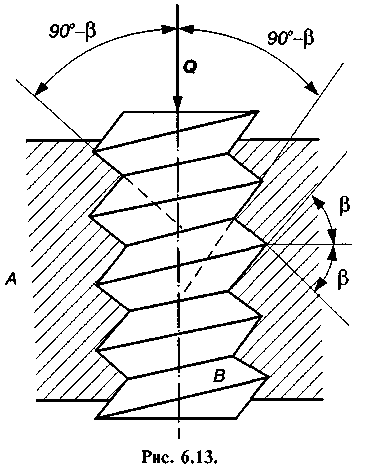
Оскільки в гвинтовій парі з гострокутною нарізкою кут 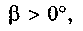то зведений коефіцієнт тертя /', а відповідно і сила тертя у такій парі більші, ніж у гвинтовій парі з прямокутною нарізкою. З цієї ж причини всі деталі нарізних з'єднань (болти, гвинти, шпильки, гайки), де треба усунути самовідгвинчування деталей, роблять з трикутною нарізкою, а в гвинтових передачах, де треба зменшити сили тертя, — з прямокутною, інколи з трапецоїдною нарізкою.

Силу FK, яку необхідно прикласти на кінці плеча радіуса R (рис. 6.12), визначають за формулами, аналогічними (6.25) і (6.26), в які замість кута тертя ц підставляють зведений кут тертя

І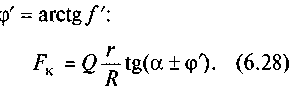

Знак "+" беруть тоді, коли напрямок переміщення гайки не збігається з напрямком осьової сили Q, і, навпаки, знак "—" — коли ці напрямки збігаються.

6.6. Тертя в обертових кінематичних парах

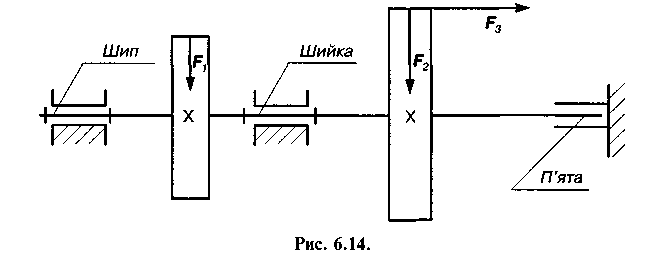
Обертові пари одержали надзвичайно широке поширення в машинах. Найхарактернішим прикладом такої пари може служити пара, утворена цапфою вала або осі та їх опорами. Цапфою називається та частина вала або осі, якою вони спираються на опори. Якщо цапфа передає на опори радіальні сили та розміщена на кінці вала, то її називають шипом (рис. 6.14), а якщо всередині вала, — шийкою. Опори в таких випадках називаються підшипниками. Якщо цапфа передає силу в осьовому напрямку, то її називають п'ятою, а опори — підп 'ятниками.

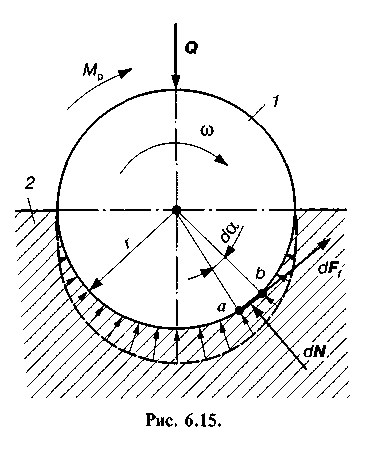
Тертя цапф у підшипниках. При виводі розрахункових формул у такій кінематичній парі використовують, як правило, дві гіпотези. Згідно з першою гіпотезою вважають, що питомий тиск с розподіляється рівномірно на проекції поверхні цапфи на горизонтальну площину (рис. 6.15), тобто

де / — довжина цапфи; d = 1г — її діаметр.

Для забезпечення рівномірного обертання вала 7, який притискається до підшипника 2 силою Q, необхідно прикласти рушійний момент Л/р, що дорівнює моменту тертя, який виникає між ланками 7 і 2.

Для визначення цього моменту розглянемо елементарну ділянку ds = ab поверхні цапфи, на яку діє нормальний тиск

де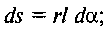/ — довжина цапфи.

Внаслідок дії сили dN на ділянці ds виникає елементарна сила тертя, яка за законом Амонтона—Кулона записується у вигляді

Ця сила створює при обертанні вала протидійний момент тертя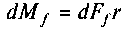, або з урахуванням (6.30) та (6.31) маємо

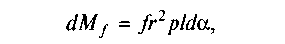
де кут da змінюється від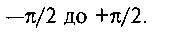

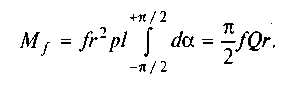
Тоді момент тертя в обертовій парі має вигляд

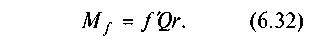
Якщо позначити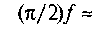 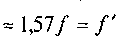— зведений коефіцієнт тертя в обертовій парі, то остаточно дістанемо

Одержана за цим припущенням (р = const) величина моменту тертя добре узгоджується з експериментальними даними для неприпрацьованих(нових) обертових пар. Для припрацьованих (старих) обертових пар більше відповідає друга гіпотеза, згідно з якою знос у напрямку дії сили однаковий. Звичайно, цапфа виготовляється з твердішого матеріалу, ніж підшипник, тому можна вважати, що під час роботи зношується тільки підшипник, а цапфа переміщається в глибину підшипника (на величину зносу) в напрямку дії сили Q. На початку роботи (до зносу) центр цапфи знаходився в точці О (рис. 6.16), через деякий час роботи він перемістився на значення зносу 5 = 00\, на стільки ж перемістилися точки, які лежать на поверхні цапфи, тобто

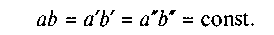
Виділимо біля точки а нескінченно вузьку смужку поверхні цапфи, площа якої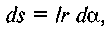де / — довжина цапфи.

Нормальний тиск на цю смужку де с — змінний

нормальний питомий тиск.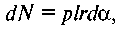

Сила тертя смужки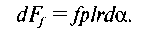 Момент тертя смужки

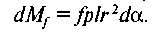Повний момент тертя визначається за формулою

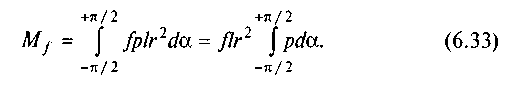
Оскільки с — змінна величина, то вона залишилась під знаком інтегралу. Виразимо с через кут а. Постійний знос д = ab у напрямку сили Q і змінний радіальний знос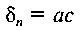зв'язані між собою співвідношенням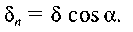

З іншого боку, радіальний знос 5„ буде прямо пропорційний питомому тиску с і відносній швидкості ковзання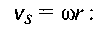

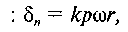де k — невідомий коефіцієнт пропорційності. Отже, 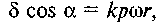звідки

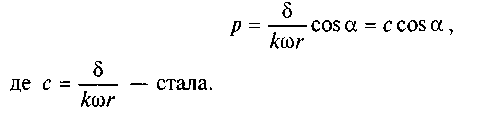
Підставивши значення с у вираз (6.33) і проінтегрувавши, знайдемо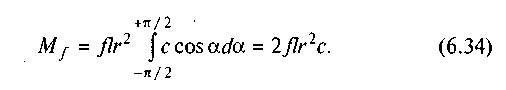

У формулі (6.34) стала с невідома. Щоб визначити її, візьмемо суму проекцій усіх сил на вертикаль: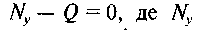— сума

проекцій елементарних реакцій dN на вертикальну вісь:

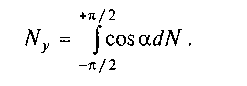
Підставивши в цей вираз значення dN = plrda і с = с cos б, візьмемо інтеграл

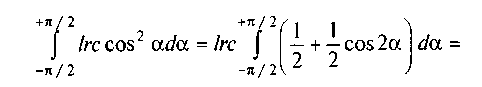
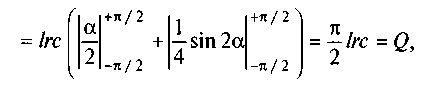
звідки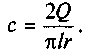

Підставивши с у вираз для моменту тертя (6.34), одержимо

Круг тертя. Якщо цапфа нерухома, нормальна реакція N підшипника проходитиме через цапфи О (рис. 6.17). Коли ж до цапфи прикласти рушійний момент Мр, вона почне обертатися в підшипнику, і при цьому виникає сила тертя, момент якої і є моментом тертя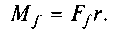Склавши силу тертя

fj з нормальною реакцією N, дістанемо повну реакцію R, яка відхилена від нормальної реакції на кут тертя ц. Момент сили тертя відносно осі цапфи можна виразити також через момент реакції Л:

де с = r sin ц .

Круг радіуса с називають кругом тертя. Повна реакція R завжди дотикається до круга тертя. Круг тертя має всі властивості конуса тертя, а саме: якщо рівнодіюча сил, прикладених до вала, проходить поза цим кругом, то вал рухається прискорено; коли рівнодіюча сил — дотична, то вал рухається рівномірно або знаходиться в стані спокою, тобто в рівновазі; якщо ж рівнодіюча проходить усередині круга тертя, то вал рухається сповільнено або перебуває в стані спокою.

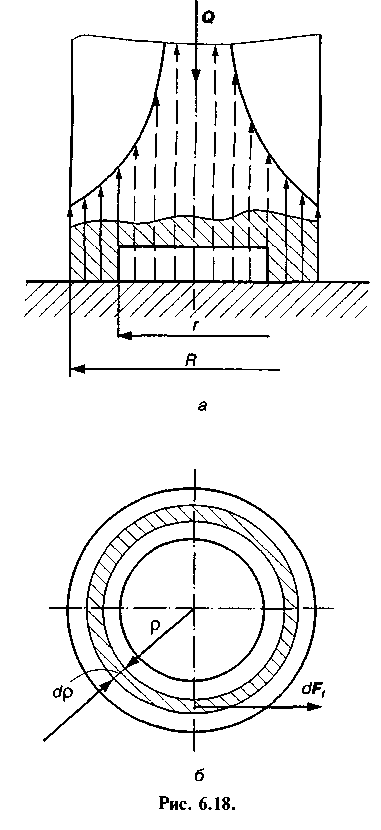
Тертя п'яти в підп'ятнику. Одним із різновидів обертових пар є п'ята, яка при роботі взаємодіє з підп'ятником в умовах тертя ковзання. Опорну поверхню вала можна виготовити у вигляді суцільного круга або кільця, як показано на рис. 6.18, а.

Для визначення моменту тертя в плоскій кільцевій п'яті також користуються двома гіпотезами. Згідно з першою гіпотезою вважають, що питомий тиск с розподіляється рівномірно по поверхні п'яти, тобто

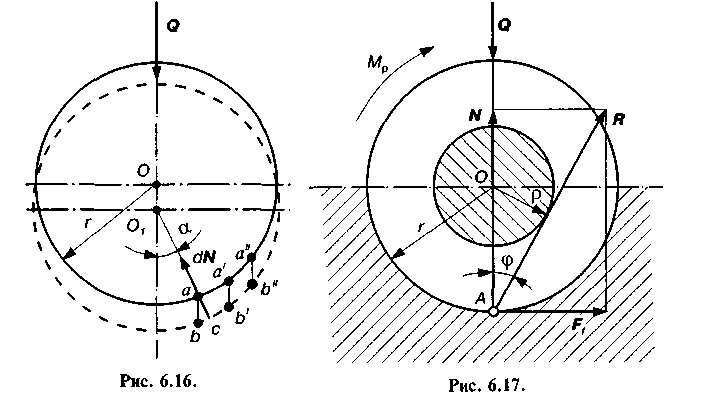
Це буде ближче до істини для неприпрацьованих кінематичних пар та для вужчого кільця, тобто чим менша різниця R — г. Елементарний момент сил тертя dMj на нескінченно вузькому кільці шириною ц (рис. 6.18, б) визначається за формулою

де dFf— сила тертя, що виникає при обертанні вала в зоні елементарного кільця. Згідно з формулою Амонтона—Кулона маємо

Нормальний тиск, що припадає на це кільце,

де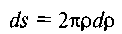— площа кільця.

Підставивши (6.39), (6.40) у формулу (6.38), маємо

Повний момент тертя кільцевої поверхні має вигляд

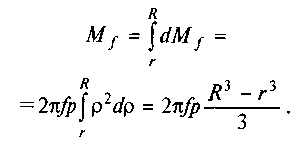
Якщо врахувати (6.37), то остаточно дістанемо

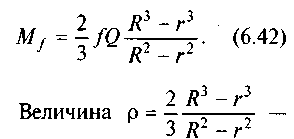
радіус тертя. Тоді

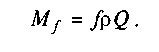
Якщо п'ята буде суцільною, то г = 0, а тому момент тертя має вигляд

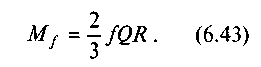
Відповідно до другої гіпотези, яка справедливіша для припрацьованих пар, знос у напрямку дії сили Q однако-· вий. У цьому випадку, перш ніж брати інтеграл з функції (6.41), треба виразити с як функцію від р, оскільки

Позначимо знос у напрямку сили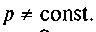Q через д, який у кожній точці кільцевої поверхні буде прямо пропорційний питомому тиску і швидкості ковзання vs= щс, тобто 5 = cpvs= сдоа> = const, де с — невідомий коефіцієнт пропорційності, звідки

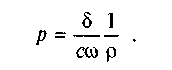
Введемо позначення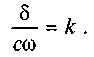Тоді

Підставивши с у вираз (6.41), після інтегрування дістанемо

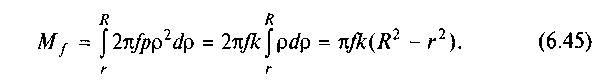
Щоб визначити невідому сталу k, візьмемо суму проекцій усіх сил на вісь вала:

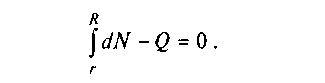
Враховуючи (6.40), одержуємо

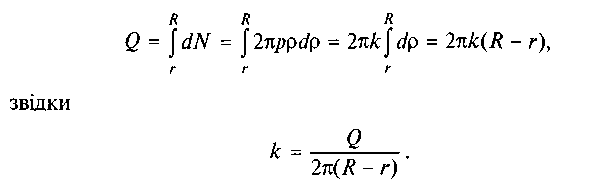
Підставивши k у вираз (6.45), знайдемо момент тертя за другою гіпотезою

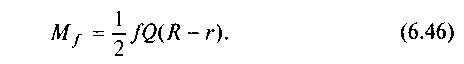
Для суцільної п'яти при г — О момент тертя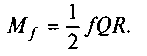

Як показує досвід, суцільна п'ята і підп'ятник зношуються нерівномірно, причому більший знос має місце на більшому радіусі. З умови (6.44) видно, що для суцільної п'яти питомий тиск розподіляється за законом рівнобічної гіперболи (див. рис. 6.18). Очевидно, що при р = 0 теоретично повинно бути 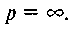Практика підтверджує, що тиск у центрі п'яти дійсно досягає досить великих значень. Це викликає зчеплення металу і відокремлення окремих частинок від більш м'якої поверхні. У результаті цього перерозподіляються питомі тиски і вони не досягають тих значень, на які вказує (6.44). Але значні нерівномірності тисків приводять до того, що з часом роботи тертьові поверхні втрачають свою початкову плоску форму.

У кільцевій п'яті знос рівномірніший, що робить її більш вигідною і зручною в експлуатації.

Тертя гнучкої ланки

У техніці широко застосовуються механізми з гнучкими ланками (пасові та канатні передачі, стрічкові гальма та транспортери тощо). У таких механізмах передача руху можлива лише при наявності достатньої сили тертя між гнучкою ланкою і шківом.

Формулу, що зв'язує основні параметри передачі гнучкою ниткою, вивів у 1765 р. Л. Ейлер [1, 4].

Для виведення цієї формули розглянемо ковзання гнучкої нитки по нерухомому шківу (рис. 6.19, а). Тоді кінець гнучкої нитки, який при своєму русі набігатиме на шків, назвемо побіжним кінцем, а той кінець, який збігатиме зі шківа, —збіжним. Дуга аЬ, по довжині якої нитка прилягає до шківа, називається дугою обхвату, а центральний кут а, що їй відповідає, — кутом обхвату. Нехай натяг набіжного кінця буде /J, а збіжного Р2. Знайдемо зв'язок між цими натягами. При цьому зробимо такі спрощення. Вважатимемо, що нитка не розтягується і не чинить опору згину при набіганні і збіганні нитки. Далі припустимо, що нитка рухається зі сталою швидкістю н. Масою нитки та її відцентровими силами інерції знехтуємо.

Щоб надати гнучкій ланці рівномірного руху в бік сили F2, необхідно подолати не тільки опір сили /є, але й силу тертя Ff між ниткою і шківом, тобто

звідки

Отже, при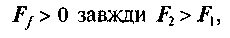а це значить, що при пере-

ході від точки а до точки Ь, де нитка набігає і збігає зі шківа, сила тертя постійно збільшується від fi до F2. Для встановлення залежності між цими величинами виділимо на дузі обхвату

нескінченно малий елемент нитки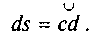 Якщо на початку

цього елемента — в точці с — натяг має деяке значення F, то в

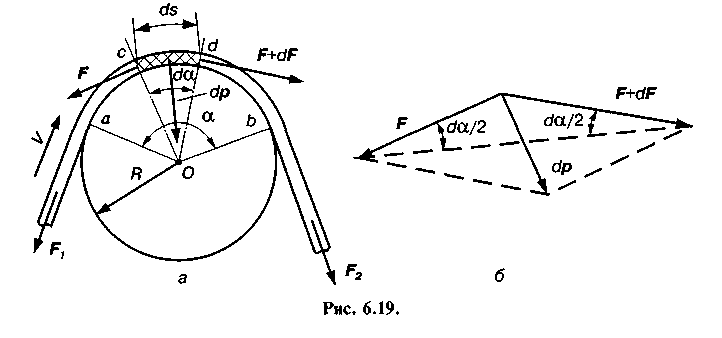
кінці його, як вказано раніше, він збільшується на df і дорівнюватиме F+ dF. Нерівномірність натягу зумовлюється наявністю сил тертя між елементом нитки і шківом. Лінії дії сил F і F + dF будуть дотичними до шківа і перпендикулярними до радіусів, проведених з точки О в точки дотику с і d.

Елементарна сила тертя dFf згідно з рівнянням (6.48) має вигляд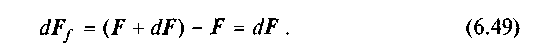

Згідно з формулою Амонтона—Кулона, сила тертя визначається за формулою

де dp — елементарна сила тиску елемента ds на шків; /— коефіцієнт тертя.

Із співвідношення (6.49) і (6.50) випливає

Позначивши через da. кут, який стягується дугою cd, знаходимо суму проекцій сил, прикладених до елемента cd, на радіус, проведений через середину дуги cd. У результаті дістанемо

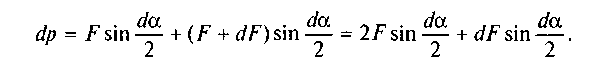
Нехтуючи нескінченно малими величинами другого порядку 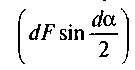і враховуючи, що для малих кутів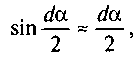одер-

жуємо

dp = Fda. (6.52)

Підставивши знайдене значення для сили dp в рівняння (6.51), дістанемо

звідки, розділивши змінні, запишемо

Інтегруючи ліву і праву частини цього рівняння, дістаємо

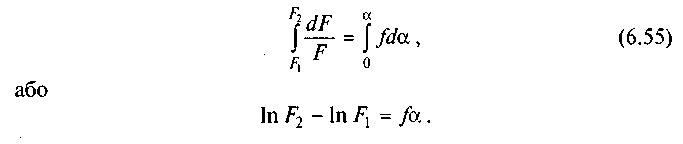
Потенціюючи цей вираз, одержуємо відому формулу Ейлера,

з якої випливає, що сила натягу зростає із зростанням кута обхвату і коефіцієнта тертя f/ Легко побачити, що при сталому коефіцієнті тертя збільшення кута обхвату дає дуже швидке зростання сили F2.

Підставивши в рівняння (6.48) значення F2 (6.56), дістанемо для сили тертя вираз

Сила Ff є тією найбільшою коловою силою, яку можна передати шківу. Якщо коловий опір на веденому шківі дорівнює або менший від сили Ff, то гнучка нитка змусить шків обертатися. Коли ж коловий опір більший від сили Ff, то гнучка ланка ковзатиме по шківу, не обертаючи його. Таким чином, натягнена силами F1 і F2 гнучка ланка при F2 > F1 може передавати веденому шківу обертовий момент

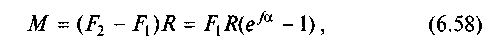
де R — радіус шківа.

Формула Ейлера дає тільки наближений зв'язок між натягами гілок гнучкої ланки. Тому останнім часом у технічній літературі рекомендуються також і інші методи розрахунку, які тут не наводяться.

6.9. Тертя кочення

Як уже зазначалося, тертям кочення називають опір, який виникає при перекочуванні одного тіла по поверхні іншого.

Цей опір виникає головним чином від того, що тіла не абсолютно тверді і завжди дещо деформуються в місцях їх стикання. Досвід показує, що опір перекочуванню тіл залежить від пружних властивостей тіл, які стикаються, їх кривизни та сили притискання.

Фізичні явища, які викликають тертя кочення, так само, як і при терті ковзання, вивчені мало. В технічних розрахунках користуються переважно даними, одержаними при експериментальних дослідженнях, які проводились над різними конкретними об'єктами: котками, колесами, роликами і шариками в підшипниках кочення тощо.

На перемагання опору під час перекочування тіл витрачається якась робота, яка йде переважно на деформацію стичних поверхонь. Якщо на коток /, який лежить на горизонтальній площині 2 (рис. 6.21, а), діє тільки сила Q, то деформація котка і опорної поверхні симетричні відносно лінії дії Q. В результаті деформації коток і опорна поверхня дотикаються не в одній точці (лінії), а деякою площиною контакту, ширина якої АВ. Реакція з боку опорної поверхні розподіляється по всій площині контакту. Згідно з положенням теорії пружності напруження в зоні контакту розподіляються за еліптичним законом. При цьому крива напружень симетрична, а значить, напрямок рівнодіючої N цих напружень збігається з напрямком сили Q. За модулем нормальна реакція N дорівнює силі Q і напрямлена в протилежний від неї бік.

Якщо на коток діє на деякій висоті h ще й горизонтальна сила F (рис. 6.21, б), то деформація котка і опорної поверхні вже несиметричні відносно лінії дії сили Q. Це пояснюється тим, що ділянка ВС буде знаходитися в зоні зростання деформації, а ділянка АС — у зоні спадання деформації (ВС > АС). Завдяки внутрішньому тертю в матеріалі тіл, що деформуються, криві навантаження і розвантаження матеріалу не збігаються (явище пружної післядії і гістерезису). Тому крива напружень у зоні СВ буде вища від кривої в зоні AC, a значить, розподіл напружень відносно лінії дії сили Q буде несиметричним з максимумом, зсунутим у бік руху котка. Отже, рівнодіюча N напружень буде зміщена в бік руху від точки С на величину k, яка називається плечем сили, або коефіцієнтом тертя кочення.

Враховуючи, що деформація тіл при коченні незначна порівняно з розмірами тертьових тіл, приймаємо, що CD = h. Тоді, записуючи рівняння моментів сил, що діють на коток, відносно точки С, маємо

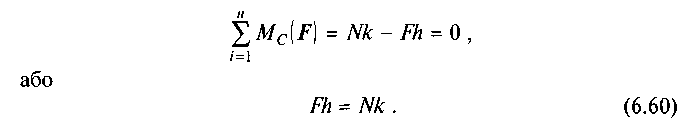
Величина Мк = Nk називається моментом тертя кочення, а Fh — обертальним (рушійним) моментом. Якщо врахувати, що N = Q, то момент тертя кочення матиме вигляд

де роль коефіцієнта пропорційності відіграє плече тертя k. Як видно з рис. 6.21 і формули (6.61), коефіцієнт тертя кочення k вимірюється одиницею довжини (мм або см), в той час коефіцієнт тертя ковзання є безрозмірна величина, і визначає максимальне значення зміщення нормальної реакції N відносно лінії дії сили Q.

Коефіцієнт тертя кочення залежить від пружних властивостей матеріалів тертьових тіл, стану їх поверхні та радіусів кривизни. На практиці, як правило, користуються значеннями, знайденими експериментальним шляхом. Наприклад, для стального колеса і рейки k ~ 0,05 мм, для гартованих стальних шариків і роликів — 0,01 мм, чавуну по чавуну — 0,05 мм, дерева по сталі — 0,3—0,4 мм, дерева по дереву — 0,5—0,8 мм.

З рівнянь (6.60) і (6.61) знаходимо силу F, яку необхідно прикласти до котка, щоб він рівномірно перекочувався по площині:

На практиці інколи користуються умовною безрозмірною величиною

яка називається зведеним (умовним) коефіцієнтом тертя кочення. Тоді залежність (6.62) набуває такого ж вигляду, як і при терті ковзання:

Втрати енергії при терті кочення, як правило, значно менші, ніж при терті ковзання. Ось чому в техніці намагаються якомога більше замінити тертя ковзання тертям кочення. Для цього широко використовується колісний транспорт, підшипники кочення, шарикові або роликові напрямні тощо.

Оскільки на практиці, звичайно, тертя кочення супроводжується тертям ковзання, то важливо розглянути, за яких умов яке тертя має місце. Тут можливі три випадки.

1. Якщо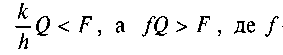— коефіцієнт тертя ковзання, то коток буде тільки котитися. Об'єднавши ці нерівності,
одержимо умову чистого кочення:

Отже, при чистому коченні необхідно, щоб зведений коефіцієнт тертя кочення (k/h) був меншим від коефіцієнта тертя ковзання.

2. Якщо ж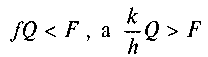, то циліндр буде тільки ков
зати. Тоді умова чистого ковзання зображується так:

При чистому ковзанні необхідно, щоб коефіцієнт тертя ковзання був меншим за зведений коефіцієнт тертя кочення.

3. Якщо ж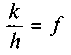, то можливе спільне кочення і ковзання,

тобто з'являється невизначеність у русі.

Розглянемо деякі приклади з техніки, де використовується тертя кочення.

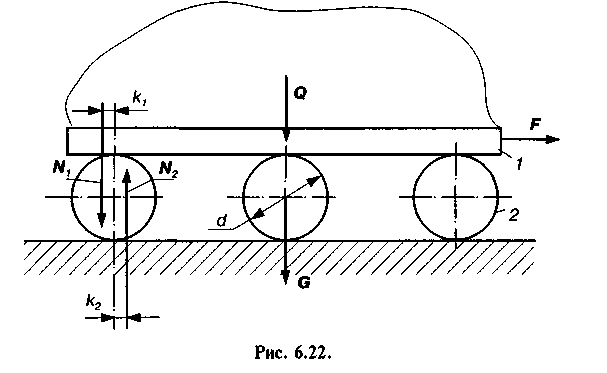
Переміщення тіл на котках. Для переміщення важких тіл (машин, верстатів, споруд тощо) на невеликі відстані часто використовують котки у вигляді циліндричних стержнів чи труб, на які спираються ці тіла або платформа з вантажем, як це зображено на рис. 6.22.

Визначимо силу F, яку необхідно прикласти до платформи 1 для рівномірного переміщення її з вантажем у горизонтальному напрямку. Позначимо через Q вагу платформи і вантажу, G — сумарну вагу котків 2, k{ і k2 — коефіцієнти тертя кочення відповідно по платформі і площині (настилу). Якщо умовно прикласти всі сили до одного котка і скласти рівняння рівноваги сил, то дістанемо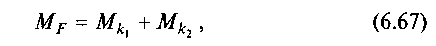

де МF = Fd — рушійний момент від сили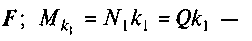 момент тертя кочення між котком і платформою (Nl = Q);

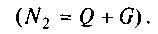
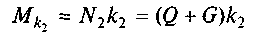— момент тертя між котком і площиною

Підставивши значення моментів у рівняння (6.67), одержимо

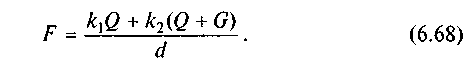
Оскільки вага котків порівняно з вагою вантажу, звичайно, мала, то нею можна знехтувати. У такому випадку

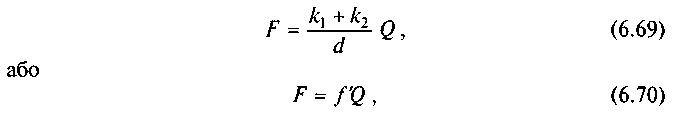
де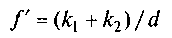— зведений (умовний) коефіцієнт тертя кочення при переміщенні вантажу на котках.

Переміщення вантажів на колесах. Для переміщення вантажів на значні відстані користуються платформами або візками, які обладнані колесами (рис. 6.23), що служать для них рухомими опорами (автомобілі, вагони та інший колісний транспорт). У цьому випадку при переміщенні вантажу з платформою треба перемогти не тільки сили тертя кочення між колесами і опорною поверхнею (дорогою), але і сили тертя ковзання в буксових вузлах, тобто між шипами і підшипниками, через які навантаження передається від платформи до коліс.

Розглянемо випадок рівномірного руху навантаженого візка з однаковими колесами (рис. 6.23). Для знаходження сили F, що забезпечує цей рух, знову умовно прикладемо всі сили і моменти сил до одного колеса та складемо рівняння його руху за один оберт (рівняння робіт):

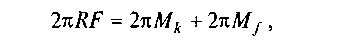
де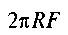— робота сили F;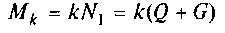— момент тертя кочення; 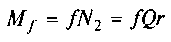— момент сил тертя ковзання в буксі.

Підставивши значення моментів, після відповідних перетворень дістанемо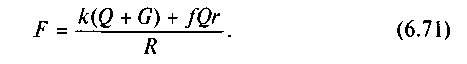

Якщо знехтувати вагою коліс, то залежність (6.71) набуває вигляду

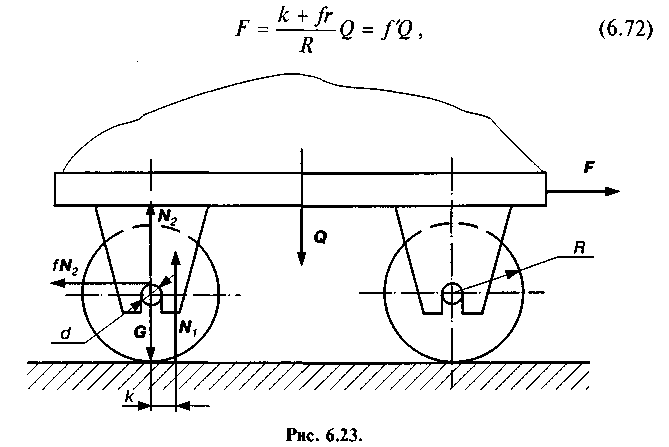
де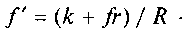— зведений (умовний) коефіцієнт тертя при

переміщенні тіл на колесах.

Якщо замість підшипників ковзання використовуються підшипники кочення, то коефіцієнт тертя /' визначається з

урахуванням зведеного коефіцієнта тертя кочення [46]: для роликових підшипників кочення

для шарикових підшипників кочення

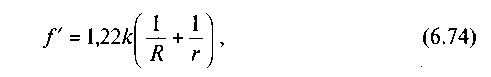
де k — коефіцієнт тертя кочення для гартованих стальних шариків і роликів; R — зовнішній радіус внутрішнього кільця підшипника; г — радіус ролика або шарика.

PAGE 1

ТЕРТЯ У ГВИНТОВИХ КІНЕМАТИЧНИХ ПАРАХ