СИНТЕЗ ВАЖІЛЬНИХ МЕХАНІЗМІВ

Лекція 26

У цьому розділі розглядається синтез плоских важільних механізмів, які досить широко використовуються у багатьох машинах, приладах і пристроях. Переваги важільних механізмів визначаються здебільшого властивостями нижчих пар, які утворюють ланки механізму. У таких парах стичними елементами ланок є поверхні, а тому питомий тиск і ступінь зносу в них менші, ніж у вищих кінематичних парах. Елементи ланок, які утворюють ці пари, виготовляються досить просто й точно, оскільки технологія обробки площин і циліндричних поверхонь ретельно і повно розроблена. Крім цього, у механізмах з нижчими кінематичними парами забезпечується стале замикання пар і на відміну, наприклад, від кулачкових механізмів, не треба використовувати пружини та інші пристрої.

Теоретично за допомогою плоских важільних механізмів можна точно відтворити будь-яку плоску алгебраїчну криву. Проте практичне використання цих механізмів обмежується тим, що їх виготовляють, як правило, багатоланковими. Із збільшенням кількості ланок у механізмі зростає ймовірність одержання недопустимих кутів передачі, збільшуються втрати потужності на тертя, відхилення від заданої залежності в результаті нагромадження похибок, викликаних неточністю виготовлення, наявністю зазорів у кінематичних парах і пружними деформаціями ланок. Тому деякі закони руху вихідної ланки практично не вдається відтворити за допомогою плоских механізмів із нижчими парами. У цьому полягає їх основний недолік. У той самий час кулачкові та зубчасті механізми завдяки різноманітності елементів вищих пар практично універсальніші, ніж важільні. Проте треба зауважити, що з розвитком методів проектування межі використання важільних механізмів розширюються.

12.1. Основні задачі синтезу та методи їх розв'язування

Якщо при аналізі механізмів розміри їх ланок вважаються заданими й необхідно знайти ті чи інші кінематичні (переміщення, швидкості, прискорення) або силові (сили, моменти сил, роботу, потужність, ККД тощо) характеристики руху, то в процесі створення механізмів і машин виникає інша (зворотна) задача: побудувати такий механізм, який би відповідав необхідним функціональним або технологічним вимогам. Ці вимоги у кінцевому підсумку зводяться до виконання деяких геометричних або механічних умов. Така задача ТММ, зворотна до задачі аналізу, називається синтезом механізмів. Отже, під синтезом механізму розуміють проектування його схеми за заданими властивостями. При цьому розрізняють три основні етапи синтезу.

Перший етап називається структурним синтезом і полягає у виборі структурної схеми механізму, що має потрібну кількість ступенів вільності, кількість та вид ланок і кінематичних пар, які забезпечують необхідні рухи ланок та їх взаємне розташування. Цей етап синтезу здійснюють на підставі довідкових даних про окремі види механізмів шляхом порівняння властивостей усіх механізмів, які можуть виконувати задані функції [3, 29, 37].

Другий етап називається кінематичним синтезом, задача якого — визначити геометричні розміри ланок, що забезпечують задані кінематичні умови роботи механізму (положення ланок, траєкторії окремих точок, швидкості та прискорення ланок і точок механізму тощо). Кінематичний синтез — один з найвідповідальніших етапів у процесі проектування механізму, оскільки якраз на цьому етапі формуються основні кінематичні властивості, необхідні для виконання механізмом покладених на нього функцій.

Якщо потрібно врахувати також динамічні властивості механізму, розв'язується більш загальна задача динамічного сиптезу, під якою розуміють проектування кінематичної схеми механізму з визначенням параметрів, що характеризують розміри та розподіл мас ланок. Динамічний синтез містить у собі два попередні види синтезу.

Отже, синтез кінематичної схеми полягає у визначенні деяких сталих параметрів, які задовольняють задані структурні, кінематичні й динамічні умови, при цьому одна частина цих параметрів може бути задана, інша — підлягає визначенню. До таких параметрів, зокрема, належить довжина ланок, положення точок їх траєкторій, значення швидкостей і прискорень, маси та моменти інерції ланок. Незалежні один від одного сталі параметри схеми механізму називають параметрами синтезу.

Параметри синтезу бувають вхідними та вихідними. Вхідні параметри задані або відомі до проведення синтезу, а вихідні визначають під час синтезу. Прикладами вхідних параметрів можуть бути наперед задана (потрібна) траєкторія руху точки механізму або необхідна продуктивність машини, а вихідними параметрами є геометричні розміри ланок (у першому випадку), а також маси ланок, закони їх розподілу, моменти інерції ланок, жорсткість пружних ланок, потужність двигуна, швидкість обертання ланок тощо.

Умови перетворення рухів, для виконання яких проектується механізм, досить різноманітні, що визначається надзвичайно широким спектром робочих функцій, які накладаються на механізми в різних машинах, приладах і пристроях сучасної техніки. Назвемо деякі вимоги, які найчастіше ставляться до механізмів:

необхідно спроектувати механізм за кількома дискретними
положеннями ланок, зокрема крайніми положеннями вихідної
ланки; при цьому закон руху ланок між заданими положеннями
не регламентується;
забезпечити відповідний закон руху вихідної ланки при за
даному законі вхідної, тобто швидкості та прискорення вихідної
ланки повинні змінюватися за деяким законом або не бути
більшими заданої величини; можуть бути задані окремі
кінематичні параметри, наприклад, середня швидкість руху,
відношення середніх швидкостей при прямому та зворотному
ході, коефіцієнт нерівномірності руху тощо;
забезпечити задані передаточні відношення двох або
більше ланок, що входять до складу механізму;
деяка точка робочої ланки механізму повинна точно або
наближено описувати задану траєкторію або деяку її частину.

Крім цього, при проектуванні механізмів треба врахувати такі фактори:

прокручування ланок, тобто можливість неперервного переходу ланки з одного заданого положення в інше, оскільки між двома заданими положеннями може виявитися проміжне, в якому рух ланок неможливий;

максимально допустимі кути тиску Фдоп, оскільки геометрично спроектований механізм може виявитися нераціональним унаслідок недопустимо великих сил, які виникають у кінематичних парах, низького ККД або навіть непрацездатним із-за явища заклинювання;

конструктивні обмеження довжин ланок механізму, оскільки при проектуванні можуть бути варіанти з недопустимо великими або дуже малими розмірами деяких ланок;

допустимі відхилення від заданого закону руху, оскільки задачу синтезу важільних механізмів за заданим законом руху найчастіше можна розв'язати лише наближено.

Серед задач, які має розв'язувати синтезований механізм, можна виділити одну або кілька найважливіших — основних задач (наприклад, отримання необхідної траєкторії руху, досягнення заданої швидкості тощо), інші вважаються другорядними — додатковими (наприклад, мінімальна вага або мінімальні габаритні розміри).

Основна задача синтезу визначає також і вид синтезу, за допомогою якого може бути розв'язана ця задача (кінематичний або динамічний синтез). Основну умову синтезу можна подати у вигляді деякої функції вихідних параметрів, яку прийнято називати цільовою функцією, або критерієм оптимізації. Додаткові умови синтезу також повинні бути відображені у математичній формі, як правило, у вигляді нерівностей.

Отже, розв'язання основної задачі синтезу здебільшого є багатопараметричним, що визначає існування багатьох розв'язків. Природно, що в такому випадку з'являється прагнення отримати кращий (оптимальний) або максимально наближений до оптимального розв'язок з урахуванням існуючих реальних обмежень (додаткових умов). Такі задачі найчастіше розв'язуються за допомогою ЕОМ (див. параграф 12.9).

Задачі синтезу механізмів можна розв'язати чотирма основними методами:

• графічним, який засновано на використанні кінематичних схем механізмів, зображених на рисунку, на якому параметри довжини побудовано у певному масштабі. Цей метод досить часто застосовується на попередніх стадіях проектування завдяки своїй простоті та наочності й переважно для плоских механізмів;

аналітичним, заснованим на різних математичних методах,
які широко використовуються завдяки повсюдній комп'ютеризації інженерної та наукової праці. Аналітичні методи, які можна застосувати в будь-яких механізмах, дають високу точність розв'язків, дають змогу отримувати оптимальні (за заданими цільовими функціями) значення параметрів синтезу. До їх недоліків слід віднести трудомісткість підготовки та налагодження
програм і не завжди достатню наочність;

графоаналітичним, що поєднує два вказані вище методи.
Цей метод дуже часто поєднує в собі високу точність обчислень
з наочністю розв'язання;

експериментальним, що використовує натуральні зразки
або моделі механізмів, які проектуються. Цей метод дає результати, найбільш наближені до реальних, але вимагає великих матеріальних витрат і слабо піддається оптимізації.

Вибір того чи іншого методу значною мірою залежить від умов, поставлених при проектуванні. Наприклад, якщо поставлена умова, щоб при наближеному виконанні заданого руху оцінити відхилення потрібного руху від фактично отриманого, то необхідно використовувати аналітичні методи, оскільки графічні методи не можуть дати повної відповіді на поставлені питання.

Далі розглядатимемо лише перші три методи, які здебільшого будуть викладені в тому вигляді, який запропоновано І. І. Артоболевським, М. І. Левитським [4, 5, 42] і частково — [25, 27, 72].

12.2. Умова існування кривошипа в чотириланкових механізмах

До найпростіших механізмів, які широко використовуються у техніці, належать шарнірні чотириланкові механізми. Основна характеристика таких механізмів — прокручування їх ланок (наявність у них одного або двох кривошипів), яке залежить від співвідношення довжин ланок. Для встановлення цієї умови розглянемо шарнірний чотириланковий механізм (рис. 12.1), в якого довжини ланок відповідно становлять 1ОА = а, 1АВ = в,lbc=c,lDC=d

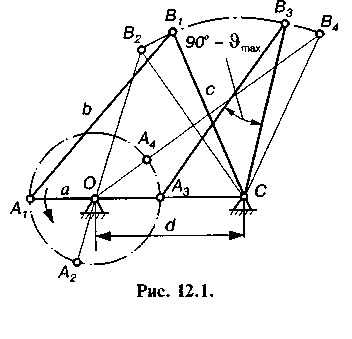
Для того щоб ланка ОА могла стати кривошипом, вона повинна при обертанні послідовно пройти через крайнє ліве ОА{ і праве ОАг положення. Тоді, прийнявши, що а — довжина найкоротшої ланки, d — найдовшої, та використавши відомі співвідношення між довжинами сторін трикутника (довжина сторони трикутника менша суми довжин двох інших сторін), записуємо такі нерівності:

a + d<b + c (12.1)

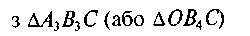
d-a<b + c. (12.2)

Незалежно від співвідношення довжин b і с нерівність (12.1) завжди забезпечує виконання нерівності (12.2). Якщо ж найдовшою ланкою буде ланка АВ або ВС (Ь > с > d або с > b > d), то нерівність (12.1) тільки підсилюється.

Нерівність (12.1) дає змогу дати загальне формулювання умови прокручування ланок шарнірного чотириланкового механізму, тобто існування кривошипа, а саме — найкоротша ланка шарнірного чотириланкового механізму може бути кривошипом, якщо сума довжин найкоротшої і найдовшої ланок менша суми довжин решти ланок. Це положення носить назву правила Грасгофа.

Використовуючи це правило, шарнірні чотириланкові механізми поділяють на три групи:

• механізм буде кривошипно-коромисловим (див. рис. 12.1),
якщо розміри його ланок задовольняють правило Грасгофа
(12.1) і за стояк прийнято ланку b або d, розташовану біля найкоротшої ланки а;

• механізм буде двокривошипним, якщо його розміри
відповідають правилу Грасгофа і за стояк прийнято найкоротшу
ланку а (рис. 12.2, а). Це випливає з того, що якщо кривошип
при виконанні правила Грасгофа виконує повний оборот
відносно стояка ОС і шатуна АВ (див. рис. 12.1), то й ці ланки
здійснюють повний оборот відносно стояка;

•механізм буде двокоро-мисловим, якщо його розміри не задовольняють правило Грасгофа, а також у випадку, коли задовольняють це правило, але найкоротша ланка є шатуном (рис. 12.2, б). Тому можливість цієї ланки бути кривошипом зникає, оскільки вона не є ланкою, розташованою біля стояка.

У граничному випадку, коли нерівність (12.1) перетворюється у рівність, усі ланки механізму в одному з крайніх положень розташовано вздовж однієї прямої. Внаслідок цього з'явиться невизначеність руху відповідної ланки (вона може рухатися або в одному, або в іншому напрямку).

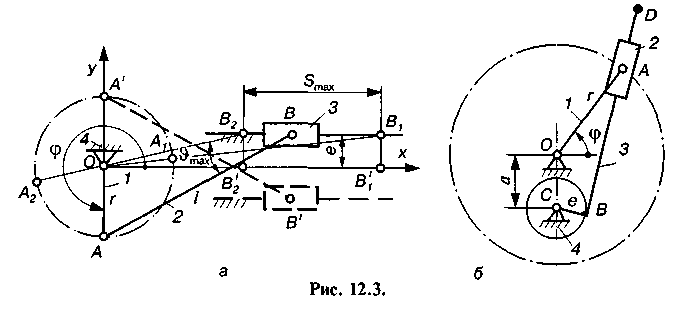
У кривошипно-повзунковому механізмі (рис. 12.3, а) ланка 1 буде кривошипом, якщо при обертанні вона пройде положення ц = 90° і 270°, що можливо, коли виконується умова

де г — довжина ланки ОА; 1 — ланки АВ; е — зміщення (дезаксіал).

Штриховою лінією зображена схема механізму, коли е < 0. Якщо г > І - е , то ланка 1 буде коромислом, і такий механізм правильніше називати коромислово-повзунним.

У кулісному механізмі (рис. 12.3, б) ланка / може бути кривошипом; ланка 3 (куліса) буде кривошипом, якщо при обертанні пройде положення ц = 270°, що можливо при виконанні умови

г>а + е, (12.4)

де г — довжина кривошипа ОА\ а = Іос — міжосьова відстань; е — зміщення куліси; е = Івс. У цьому випадку маємо механізм з обертовою кулісою. Якщо г < а + е, то куліса 3 буде коромислом (механізм з коливальною кулісою). Найбільш розповсюджені кулісні механізми, в яких зміщення е = 0.

12.3. Синтез механізмів за заданими законами руху ланок

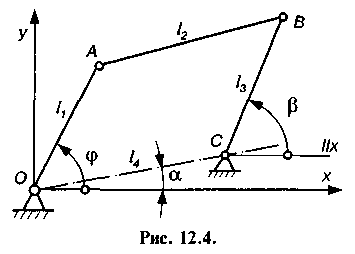
Розв'язання задачі про відтворення заданого руху ланок покажемо на прикладі шарнірного чотириланкового механізму (рис. 12.4). Нехай закон руху вхідної ланки ОА задано у вигляді залежності його кута повороту ц від часу t, тобто

Ц = Ф(0, (12.5)

а закон руху вихідної ланки ВС — у вигляді залежності його кута повороту в також від часу t, тобто

в = в(0· (12.6)

Вилучаючи з рівнянь (12.5) і (12.6) час, записуємо функцію положення

в = в(ц). (12.7)

Закон руху вихідної ланки можна задати також у вигляді передаточної функції /31 — аналога кутової швидкості <р'3 (див. параграфи 3.6—3.8):

де (оь щ3 — кутова швидкість ланки відповідно 7 і 3.

За цією причиною механізми, які дають змогу відтворити задану функціональну залежність (12.7) або (12.7') між переміщеннями ланок, що утворюють кінематичні пари зі стояком, називають передаточними.

Зв'язок між кутами ц і в встановлюємо за допомогою розмірів ланок механізму, які

називають параметрами кінематичної схеми механізму або скорочено параметрами синтезу. Отже, щоб задовольнити умову (12.7), необхідно відповідним чином підібрати параметри механізму. Для механізму, зображеного на рис. 12.4, кількість незалежних параметрів може дорівнювати шести. Це довжини

ланокпочаткове значення ц0 кута ц і кут а, який утворює стояк ОС з віссю Ох. Якщо прийняти довжину /! кривошипа ОА за одиницю вимірювання довжин ланок і виразити розміри ланок через відносні параметри:

то отримаємо п'ять параметрів синтезу (л2, л3, л4, ц0 і ос), які необхідно визначити.

Маючи заданими закони руху ланок ОА і ВС, можна визначити окремі положення цих ланок. Позначимо кути, які утворюють ланки ОА і ВС з віссю Ох (рис. 12.4), відповідно ц,, <с2, <р?, ..., срт і Рь Р2, Рз, ..., Р„. Тоді згідно з (12.7) матимемо систему рівнянь:

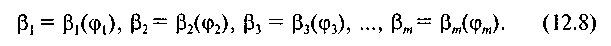
Якщо число рівнянь (12.8) дорівнює числу параметрів, які треба визначити, то задачу теоретично можна повністю розв'язати. У практичних задачах внаслідок ускладнень при спільному розв'язанні рівнянь (12.8) число т пар заданих відповідних значень кутів ц і в вибирають таким, що дорівнює числу параметрів, які необхідно визначити. У такій постановці задача про відтворення заданого закону руху називається задачею про положення і розглядається далі.

12.4. Синтез механізмів за заданими положеннями ланок

Розглянемо задачу про синтез шарнірного чотириланкового механізму (рис. 12.5, а) за заданими положеннями його ланок.

Для спрощення задачі слід припустити, що нерухомі шарніри О і С розташовані на осі Ох, від якої ведеться відлік кутів ц і в, і прийняти, що кут б = 0, то при заданих довжинах ланок будь-якому заданому значенню ц, кута ц (рис. 12.5, б) відповідатиме цілком визначене значення в, кута в, а тому кількість параметрів механізму, які необхідно визначити, дорівнюватиме трьом (див. параграф 12.3). Це параметри л2 =

Отже,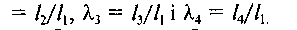якщо будуть задані три положення ланки ОА (рис.

12.5, б) кутами ц[; ц2, ц3, а три відповідні їм положення ланки
ВС — кутами в,, в2, в3, то завжди будуть визначені параметри
л2, л3, л4, оскільки кількість рівнянь вигляду (12.8) дорівнює
кількості цих параметрів.

Поставлену задачу можна розв'язати аналітичним і графічним методами.

Аналітичний метод. Зобразимо сторони механізму (рис. 12.6) у вигляді векторів л,, л2, л3, л4, причому л] = 1. Тоді маємо

л, + л2 = л4 + л3. (12.9)

Проектуємо обидві частини рівнянь (12.9) на осях Ох, Оу. Позначимо кут, утворений шатуном АВ з віссю Ох, буквою д і отримаємо для довільного /-го положення механізму рівняння проекцій на осях Ох і Оу у вигляді

або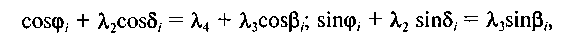

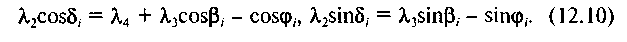
Підносимо почленно рівняння (12.10) до квадрата і додаємо їх. Тоді отримаємо

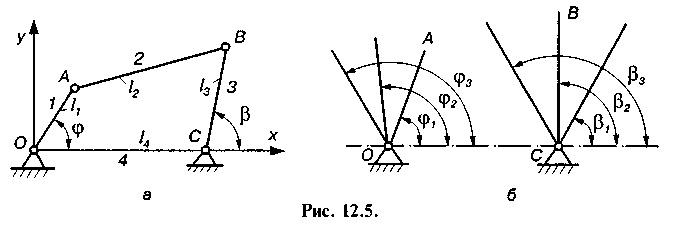
Перенесемо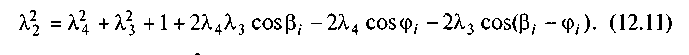л\ у праву частину (12.11) і поділимо всі члени на 2л4. Розв'язуючи рівняння відносно cos ц,, матимемо

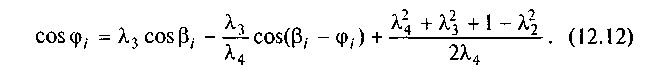
Введемо позначення:

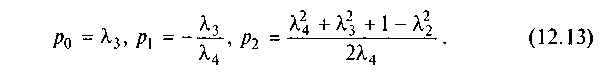
Тоді (12.12) запишеться так:

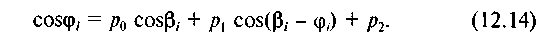
Підставляючи у рівність (12.14) задані кути ц,, ц2, ц3 і в,, в2, в3 (див. рис. 12.5, б), записуємо систему, складену із трьох лінійних рівнянь:

Розв'язуючи сумісно цю систему рівнянь, визначаємо величини коефіцієнтів р0, />!, р2, після чого за допомогою співвідношень (12.13) можна знайти невідомі параметри л2, л, і л4.

Якщо необхідно спроектувати механізм за двома положеннями ланок ОА і ВС, то один із параметрів механізму можна задати довільно і задача матиме нескінченну кількість можливих розв'язків.

Такі задачі можна розв'язати графічним методом за допомогою нескладних геометричних побудов.

Синтез механізмів за двома заданими положеннями шатуна. Нехай задано два положення /Й,в, і А2В2 шатуна шарнірного чо-тириланкового механізму (рис. 12.7). Необхідно знайти положення точок О і С — центрів обертання ланок механізму, які входять у кінематичні пари зі стояком. Точки А\ і А2 повинні лежати на колі з центром у точці О, а точки Bt і В2 — на колі з центром С. Оскільки через дві точки можна провести нескінченну кількість кіл, то геометричним місцем цих кіл є прямі 11 або 22, які перпендикулярні до хорд AtA2 або В{В2 і проходять через їх середину N або М. Точку О можна розмістити у будь-якій точці прямої 7/, а точку С — прямої 22. Отже, для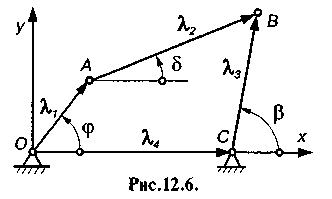

вказаного завдання можна побудувати нескінченну кількість механізмів, які задо вольняють задані умови. Додаткові умови можна накласти, якщо, наприклад, поставити умову, щоб механізм був двокривошипним або кривошипно-коромисловим тощо.

Якщо вимагається, щоб одна із точок ланки АВ, наприклад точка В, рухалась вздовж нерухомої прямої хх, то центр С кола повинен знаходитися у нескінченності, обертова пара С перетворюється у поступальну (рис. 12.7, б), тоді отримаємо кривошипно-повзунковий механізм.

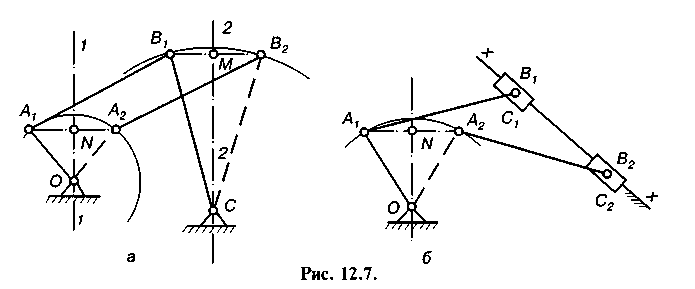
Можна поставити додаткову вимогу, щоб при заданому переміщенні шатуна АВ кути повороту ц і в відповідно ланок ОА і ДС були також заданими (рис. 12.8). Тоді з'єднуємо точки А\ і А2 прямою і відкладаємо при точках А{ і А2 кути, що дорівнюють 90° - ц/2. Точка перетину О прямих Бгб\ і А2а2 визначить положення осі О обертання ланки ОА. Так само, якщо з'єднати точки В\ і В2 і при цих точках відкласти кути 90° - в/2, то точка С перетину прямих Btb{ і В2Ь2 визначить положення осі обертання С ланки ВС.

Синтез механізмів за трьома положеннями шатуна (рис. 12.9). Задача зводиться до знаходження центра кола, яке проходить через три точки. Як відомо, ця задача має тільки один розв'язок. Отже, маючи три точки А\, Б2, А3, з'єднуємо прямими

PAGE 1

СИНТЕЗ ВАЖІЛЬНИХ МЕХАНІЗМІВ