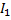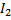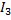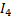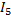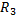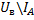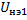Расчет линейных электрических цепей постоянного тока

PAGE \* MERGEFORMAT 1

Содержание

Введение……………………………………………………………………………………………………………………………2

Расчет линейных электрических цепей постоянного тока ………………………………………3
1. Расчет нелинейных электрических цепей постоянного тока ………………………………….9

2.1 Расчет однофазных электрических цепей переменного тока ………………………………..11

2.2 Расчет трехфазных электрических цепей переменного тока…………………………………13

2.3 Исследование переходных процессов в электрических цепях………………………………15

Заключение…………………………………………………………………………………………………………………………

Список используемой литературы……………………………………………………………………………………

Введение

Электротехника является областью науки, которая занимается изучением электротехнических и магнитных явлений и их техническим использованием в практических целях.

Интенсивное использование электрической энергии связано со следующими ее особенностями: возможностью достаточно простого и экономичного преобразования в другие виды энергии (механическую, тепловую, лучистую и т.д.); возможность централизованного и экономичного получения на различных электростанциях; простой передачи с помощью линий электропередачи с малыми потерями на большие расстояния к потребителям.

Высокая рентабельность и конкурентоспособность современных предприятий базируется на полной механизации и автоматизации производственных процессов. Решение этих задач требует создания автоматизированных систем управления на основе современной электротехнической и электронной аппаратуры и электрооборудования. Во всех отраслях производства с помощью электротехнической аппаратуры осуществляется управление производственными механизмами, автоматизация их работы, контроль за ведением производственного процесса, обеспечение безопасности обслуживания и т.д. Следовательно, функции электротехнических устройств машин настолько значительны по сравнению с их механической частью, что именно они во многом определяют такие важные показатели, как производительность, качество и надежность создаваемой продукции.

В курсе "Общая электротехника" осуществляется анализ явлений, происходящих в электрических и магнитных цепях. Изучаются вопросы связанные с установившимися и переходными процессами, с расчетами цепей постоянного переменного тока, с устройством и принципом действия трансформаторов, электромагнитных устройств, электрических машин постоянного и переменного тока, информационных электрических машин.

Анализ электрического состояния линейных и нелинейных электрических цепей постоянного тока

Расчет линейных электрических цепей постоянного тока

Для электрической цепи выполнить следующее:

Составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;
Определить токи во всех ветвях схемы, используя метод контурных токов;
Определить токи во всех ветвях схемы на основании метода наложения;
Составить баланс мощностей для заданной схемы;
Результаты расчетов токов по пунктам 2 и 3 представить в виде таблицы и сравнить;
Определить ток во всей ветви методом эквивалентного генератора;
Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

Дано:

Е1=20В; Е2=30В; R1= 54 Ом; R2=43 Ом; R3=32 Ом; R4=26 Ом; R5=51 Ом; R6=12 Ом;

1. Составим на основаниях законов Кирхгофа систему уравнений для определения для определения токов во всех ветвях системы. Произвольно задаем направление токов в ветвях(I1..I5). Число токов равно числу ветвей. Т.к. на схеме 5 ветвей то необходимо для определения токов составить 5 уравнений. Составим уравнения для узлов по 1-му закону Кирхгофа, т.к. в схемы 3 узла (A, B и C).

Узел B ;

Узел С .

Задаемся обходом каждого контура и составляем уравнение и составляем уравнения по второму закону Кирхгофа.

Контур САС – обход против часовой стрелки

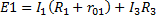
Контур AA’BC – обход по часовой стрелке

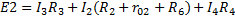
Контур А’BA’ – обход против часовой стрелки

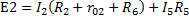
2. Расчет по методу контурных токов

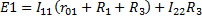
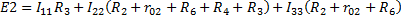
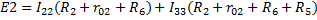
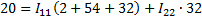
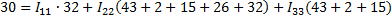
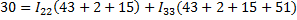
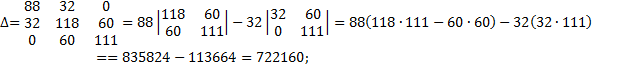
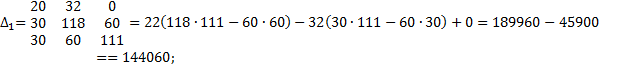
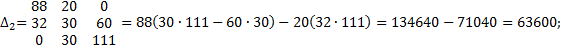
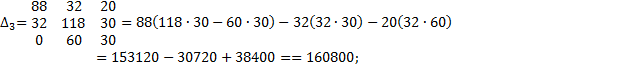
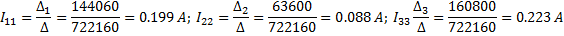
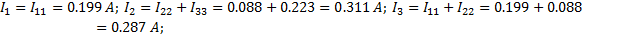
3. Метод наложения

Отсутствует

Ом

;

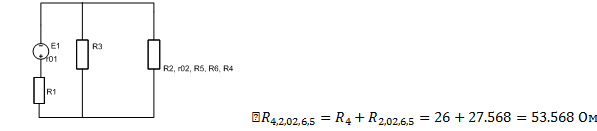
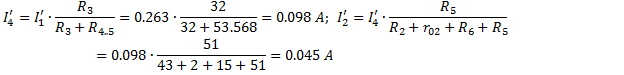
Отсутствует

;

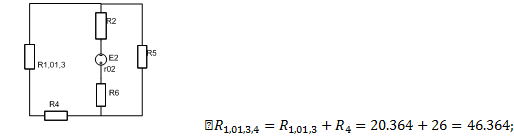
Ом;

; ;

;

Токи ветвей

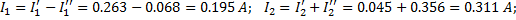
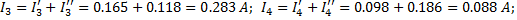
4. Составим баланс мощностей для заданной цепи. Т.к. токи в ветвях совпадают по направлению с направлением ЭДС, то мощности источников:

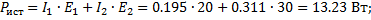
Мощности, рассеиваемые в сопротивлениях, определяем по формуле :

Вт;

Мощности, рассеиваемые на сопротивлениях, практически совпадают с суммой мощностей источников.

5. Результаты по пунктам 2 и 3.

Метод контурных токов	0,199	0,311	0,287	0,088	0,223
Метод наложения	0,195	0,311	0,283	0,088	0,223
I

6. Определение тока второй ветви методом эквивалентного генератора

Преобразуем схему. Приведем ее к виду.

Для определения сопротивлений на выводах a и b, выделим схему активного двухполюсника. Рассчитаем ток холостого хода активного двухполюсника. Преобразуем схему к удобному для расчета виду

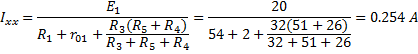
Эквивалентное сопротивление схемы относительно точек a и b

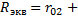
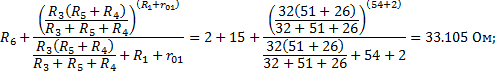
Разность потенциалов между a и b

Тогда

Величина совпадает с расчетом по методу контурных токов (0,311)

7. Построение потенциальной диаграммы

Выбираем замкнутый контур, содержащий обе ЭДС

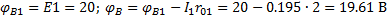
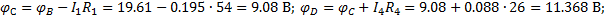
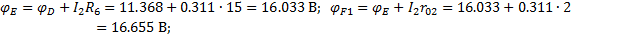
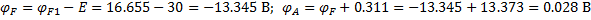
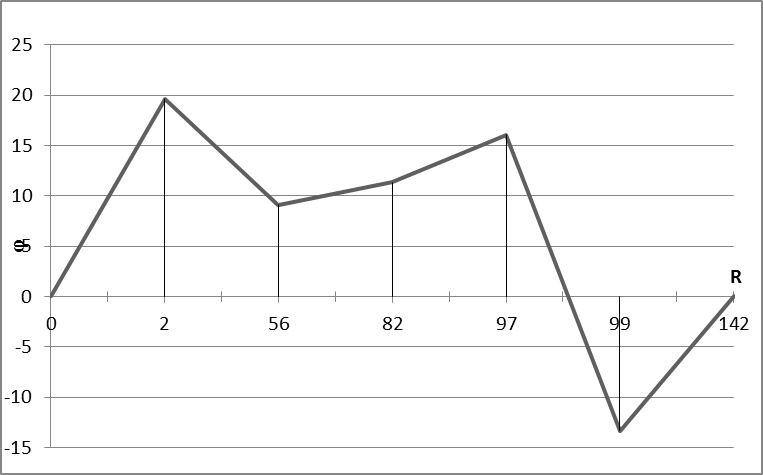
1.2. Расчет нелинейных электрических цепей постоянного тока.

Построить входную вольтамперную характеристику схемы нелинейной электрической цепи постоянного тока. Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики «а» и «б»

Дано: нэ1; нэ2.

Строим ВАХ параллельного соединения и нэ2.

Задаемся рядом напряжений и определяем токи. Результирующий ток равен сумме токов при заданном напряжении. Характеристику линейного элемента стоим по 2-м точкам, т.к. это прямая. . Строим ВАХ параллельного соединения R и нэ2. Падение напряжения на них одинаково.

I\U	20	40	60	80
	0,65	1,25	1,9	2,5
нэ2	0,35	0,6	1,1	1,5
I	1	1,85	3	4

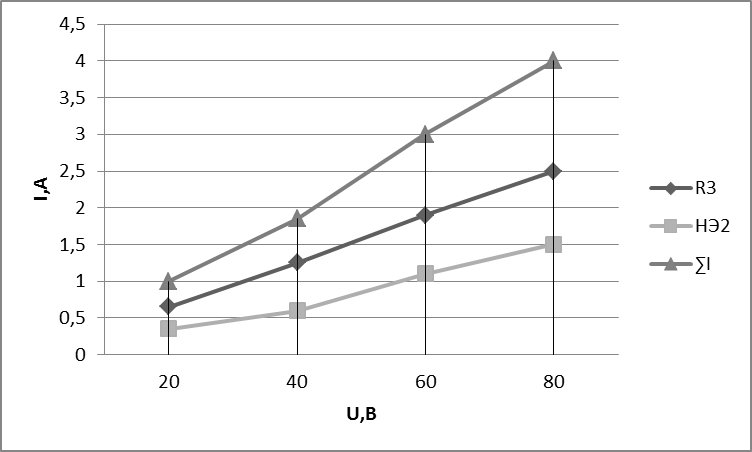
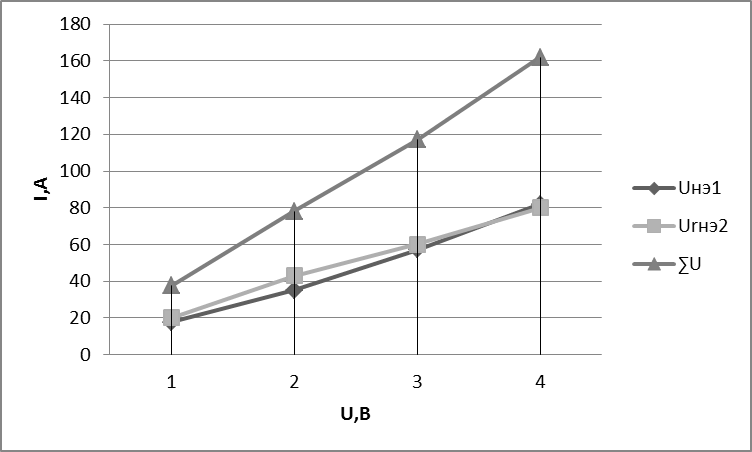
Строим ВАХ последовательного соединения нэ1 с параллельным соединением нэ2 и . Задаемся рядом токов рядом токов и определяем напряжение по этим токам. Напряжение результирующей кривой при заданном токе определяется как сумма напряжений, определяемых из графиков .

	1	2	3	4
	17,5	35	57	82
	20	43	60	80
U	37,5	78	117	160

Анализ электрического состояния линейных электрических цепей переменного тока: однофазных, трехфазных. Исследование переходных процессов в электрических цепях.

2.1 Расчет однофазных линейных электрических цепей переменного тока

К зажимам электрической цепи подключен источник синусоидального напряжения с частотой f= 50 Гц. Выполнить следующие:

Начертить схему замещения электрической цепи, рассчитать реактивные сопротивления элементов цепи;
Определить действующие значения токов во всех ветвях цепи;
Записать уравнение мгновенного значения тока источника;
Составить баланс активных и реактивных мощностей;
Построить векторную диаграмму токов, совмещенной с топографической векторной диаграммой напряжений.

Дано: ; =30; f=50 Гц.

Расчет реактивных сопротивлений

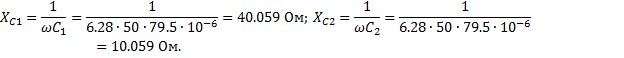
2. Преобразуем схему.

Общее сопротивление

Z=20-i80.178+19.16+i14.44=39.16-i65.74=76.52

Действующие значение напряжения

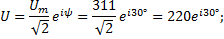
Токи ветвей

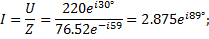
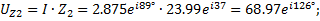
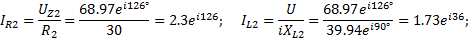
3. Мгновенное значение тока источника

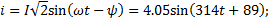
4. Комплексна мощность цепи

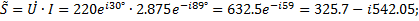
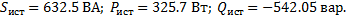
Мощности приемников

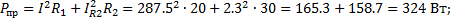
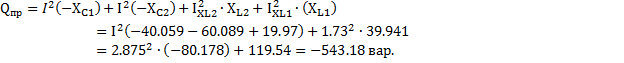
Баланс выполняется.

5. Напряжение на элементах схемы

Задаемся масштабам

;

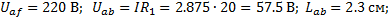
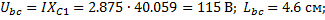
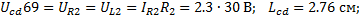
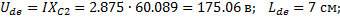
2.2 Расчет трехфазных электрических цепей

В соответствии с данными начертить схему соединения сопротивлений в трехфазной цепи.

Определить:

Фазные токи;
Линейные токи (при соединении треугольником);
Ток в нулевом проводе (при соединении звездой);
Активную, реактивную и полную мощность каждой фазы и всей трехфазной цепи;
Угол сдвига фаз между током и напряжением в каждой фазе;
Начертить в масштабе векторную диаграмму трехфазной цепи.

Дано:

2.1 Фазные напряжения в комплексной форме

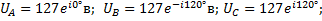
Сопротивление фаз в комплексной форме

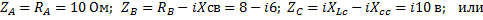
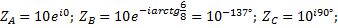
Комплексы фазных токов

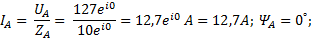
=1,55 - i12,61; ;

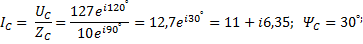
2.2 Вычислим ток в нейтрали

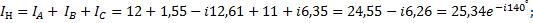
2.3 Мощности фаз и всей цепи. Полные мощности фаз.

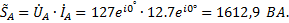
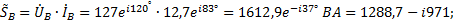
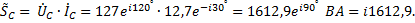
Полная мощность цепи

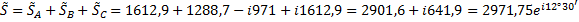
Таким образом,

Для фазы A =1612,9 Вт;

Для фазы В

Для фазы С

Для всей цепи S=2971,75 ВА; P=2901,6; Q=641 Вар.

2.5 Векторная диаграмма цепи

Масштаб тока 4 А/см

6.33

2.3 Исследование переходных процессов в электрических цепях

При размыкании выключателя цепь содержащая катушку индуктивности или конденсатор, подключается е источнику постоянного напряжения или отключается от него.

Определить практическую длительность переходного процесса, ток в цепи и энергию электрического или магнитного поля при t=3. Построить график i=f(t); и =f(t)

Дано: L=0.5 Гн; R=25 Ом; =25 Ом; Г=50 В

1. Подключаем катушку к источнику.

Для замыкания (t=0) ток в цепи до начала переходного процесса i(0)=0.

После окончания переходного процесса

Закон изменения переходного тока

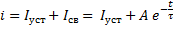
свободная составляющая переходного тока,

A – постоянная интегрирования,

Определим постоянную интегрирования, полагая t=0,

, так как по закону коммутации i(0)=0

Закон изменения переходного тока

Практическая длительность переходного процесса t=5

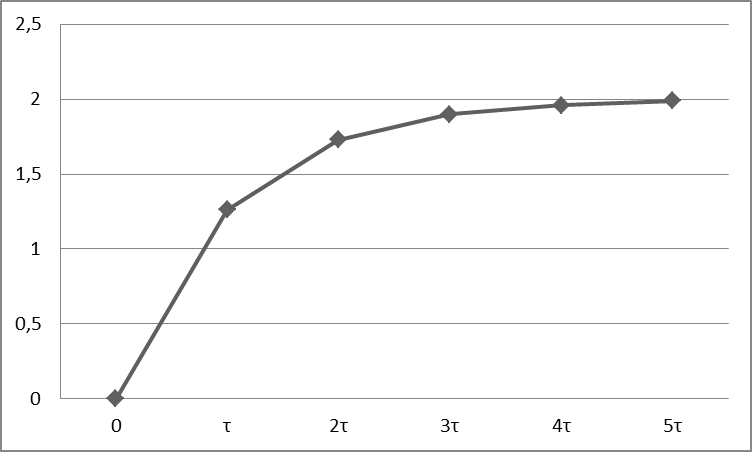
Строим график переходного процесса. Задаёмся t=0; t= t=2

t,c

i(t)

1,26

1,73

1,9

1,96

1,99

Закон изменения самоиндукции

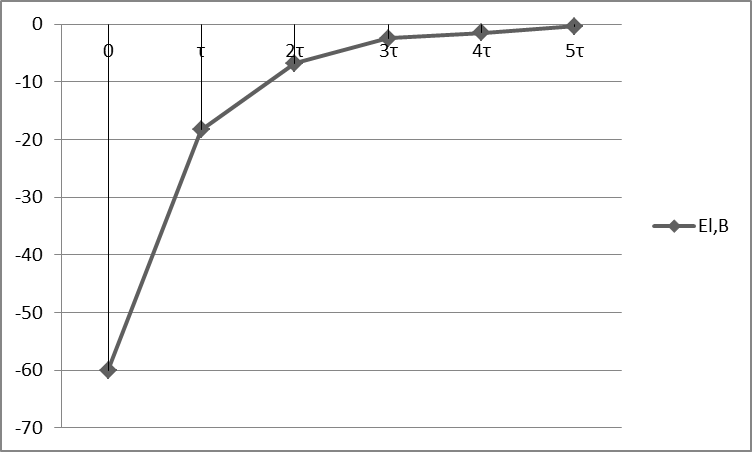
Строим график . Определяем при t =0; t= t=2

t,c	0		2	3	4	5
El,В	-60	-18,35	-6,75	-2,45	-1,5	-0,35

Энергия магнитного поля

= при i=1,9A;

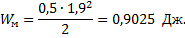
2. Отключаем катушку от источника питания

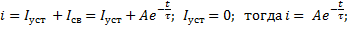
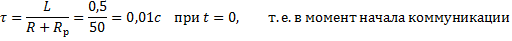
i(0)=2A; A=2 i=2

Длительность переходного процесса

Закон изменения ЭДС самоиндукции

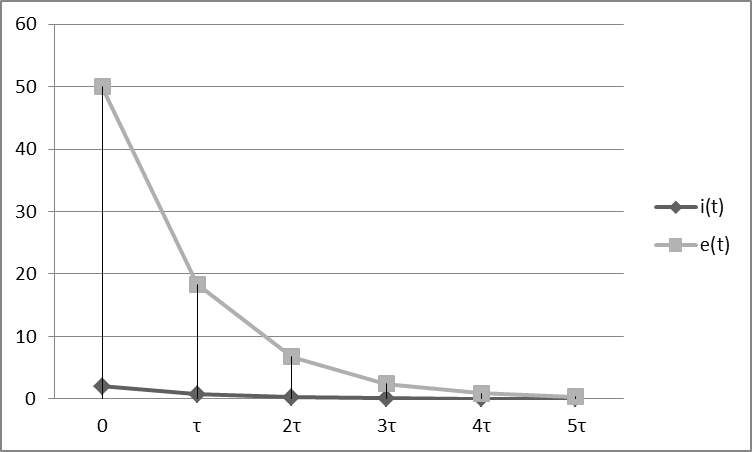
Строим графики i(t) и e(t).

t,c	0		2	3	4	5
i(t)	2	0,73	0,27	0,098	0,036	0,004
e(t)	50	18,33	6,75	2,45	0,9	0,35

Вывод

За время выполнения работы было усвоено:

Методика расчета линейных электрических цепей постоянного тока
Методика расчета нелинейных электрических цепей постоянного тока
Методика расчета однофазных электрических цепей переменного тока
Методика расчета трехфазных электрических цепей переменного тока
Исследование переходных процессов в электрических цепях

Список используемой литературы:

А.С.Касаткин, М.В.Немцов «Электротехника» Москва 2000г.
Г.И.Атабеков, С.Д.Купалян, А.Б.Тимофеев, С.С.Хухриков «Теоритические основы электротехники» Москва 1966г.

Расчет линейных электрических цепей постоянного тока