АНАЛІТИЧНІ МЕТОДИ КІНЕМАТИЧНОГО ДОСЛІДЖЕННЯ МЕХАНІЗМІВ

ЛЕКЦІЯ N10

АНАЛОГИ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ

Аналітичне дослідження кінематики механізмів зручно вести з використанням аналогів швидкостей і прискорень. Це пояснюється тим, що для заданої кінематичної схеми механізму аналоги швидкостей і прискорень залежать тільки від узагальненої координати і не залежать від швидкості руху початкової ланки. Важливо зазначити, що аналоги швидкостей і прискорень дають змогу легко порівнювати закони руху ланок, а звідси й вибрати оптимальний варіант механізму для забезпечення заданих умов роботи.

Якщо кут повороту якої-небудь k-ї ланки задано як функція

(1)

де - кут повороту початкової ланки, то кутова швидкість k цієї ланки може бути представлена так:

(2)

де, - кутова швидкість початкової ланки [ ];

- безрозмірна кутова швидкість ланки (аналог кутової швидкості) чи передатна функція кутової швидкості.

Отже, дійсна кутова швидкість k дорівнює добутку кутової швидкості початкової ланки на аналог кутової швидкості ланки к.

Диференціюючи рівняння (2) за часом t маємо величину кутового прискорення ланки к:

(3)

де - аналог (передатна функція) кутового прискорення.

Аналогічно можуть бути отримані рівняння для швидкості і прискорення якої-небудь точки ланки k.

Нехай rm є радіус-вектор, який визначає положення точки m. Тоді швидкість точки m

, (4)

де, - аналог швидкості точки m (має розмірність одиниць довжини).

Таким чином, дійсна швидкість точки m дорівнює добутку кутової швидкості початкової ланки на аналог швидкості точки m.

Диференціюючи вираз (4) за часом маємо величину прискорення а точки m:

де, - аналог прискорення точки m (має розмірність одиниці довжини). Рух початкової ланки механізму при a = const називається перманентним чи основним рухом механізму. При цьому = 0, тоді: ; (10)

; (11)

; (12)

. (13)

Якщо в рівностях (2 - 5) прийняти кутову швидкість =0, то кутові і лінійні швидкості ланок також дорівнюють нулю, а кутові і лінійні прискорення визначаємо за формулами:

(14)

(15)

Рух ланки, описаний рівняннями (10), (11) називається початковим.

2. АНАЛІТИЧНЕ ДОСЛІДЖЕННЯ КІНЕМАТИКИ ЧОТИРИЛАНКОВОГО МЕХАНІЗМУ З ДВОПОВОДКОВОЮ СТРУКТУРНОЮ ГРУПОЮ II КЛАСУ 2 ПОРЯДКУ 1 ВИДУ

Розглянемо схему кривошипно-коромислового механізму.

Механізм може мати 2 схеми зібрання (рис.1, а, б) і утворюється вхідною ланкою АВ і структурною групою першого виду з трьома обертальними кінематичними парами В,С,D.

Рівняння замкненого векторного контуру, що утворений ланками механізму, має такий вигляд:

. (16)

Проектуючи рівняння (4.1) на осі нерухомої системи координат ОХУ і враховуючи, що , маємо:

; (17)

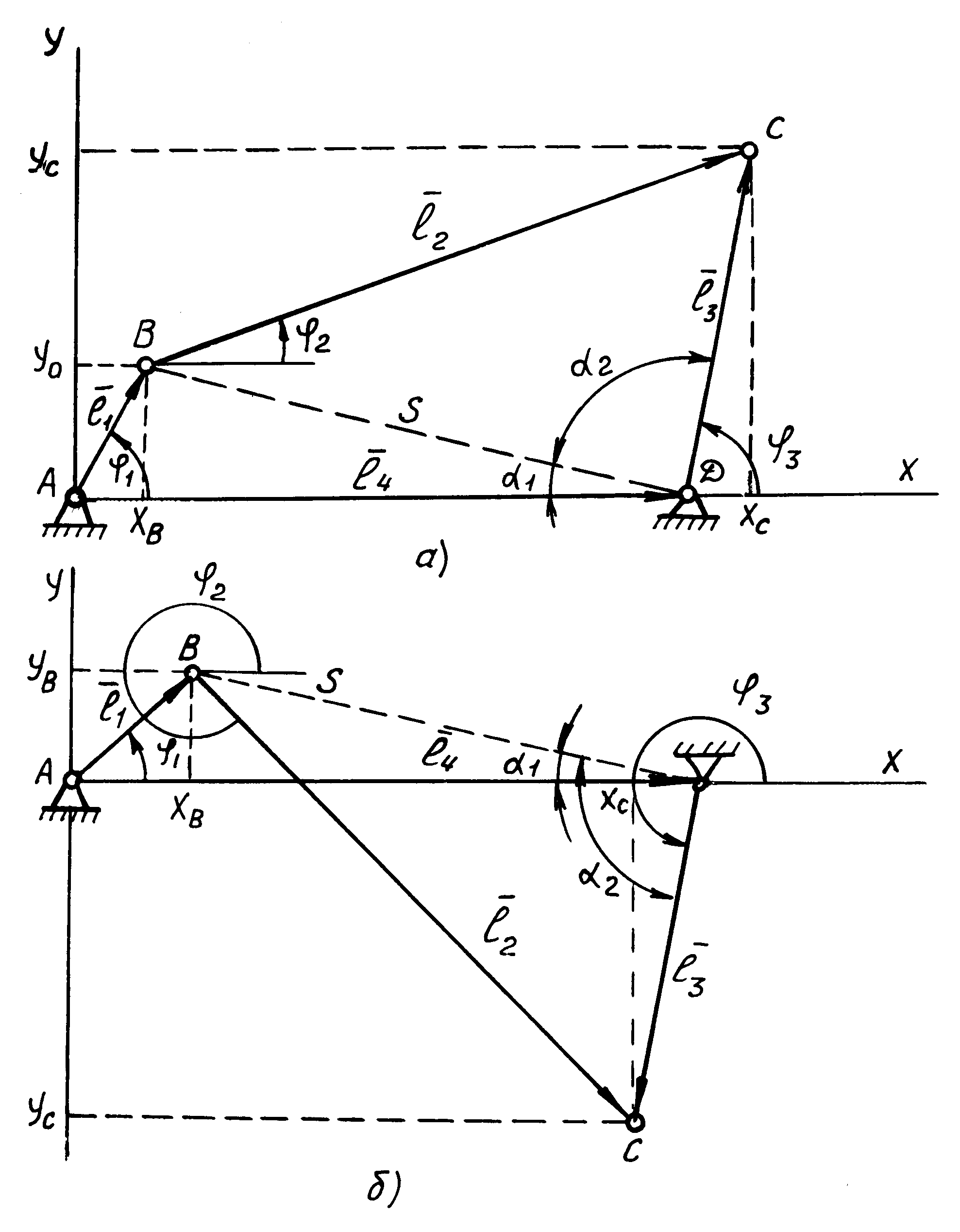
Рис.4.1 Схема кривошипно-коромислового механізму.

Координати точки В:

; (18)

. (19)

Задачу визначення положень механізму розв’язуємо поділом замкненого контуру АВСD на 2 трикутники: АВD і ВСD.

Розглянемо АВD і ВСD для яких будуть справедливими такі залежності:

;

1= (20)

;

S = (21)

Напівпериметр ВСD:

. (22)

Радіус кола вписаного в ВСD:

. (23)

Допоміжний кут:

Кутова координата ланки DС:

, для схеми (рис. 4.1 а); (24)

, для схеми (рис. 4.1 б), (25)

тоді координати точки С:

; (26)

. (27)

Кут 2 визначаємо через координати точок С і В:

(сх. 1);

(сх. 1,2);

2 = (сх. 2); (28)

(сх. 2);

(сх. 2).

Для визначення аналогів швидкостей продиференціюємо систему (17) по узагальненій координаті 1:

; (29)

Позначимо: ,

де, - аналоги кутових швидкостей відповідно 2 і 3 ланок, тоді систему (4.14) запишемо у такому вигляді:

; (30)

. (31)

Від кутів, які входять у рівняння (4.15) віднімаємо спільний кут 2 , що рівнозначно повороту системи координат ХАY на кут 2:

, (32)

звідки:

. (33)

Після аналогічного перетворення рівняння (30) поворотом координатних осей на кут 3 маємо:

, (34)

звідки:

. (35)

Для аналогів кутової швидкості можна записати:

; (36)

, (37)

тоді кутові швидкості другої і третьої ланок:

; (38)

. (39)

Лінійні швидкості точок:

; (40)

. (41)

Для визначення кутових прискорень ланок 2 і 3 диференціюємо систему (30-31) по узагальненій координаті 1:

; (42)

, (43)

де - аналоги кутових прискорень, які визначимо, якщо виконати перетворення координат послідовним поворотом їх осей на кути -2, -3.

(44)

. (45)

Кутові прискорення ланок:

; (46)

, (47)

де - задані кутова швидкість і кутове прискорення початкової ланки .

Прискорення точки С визначимо за формулою:

. (48)

3. ЧОТИРИЛАНКОВИЙ МЕХАНІЗМ З ДВОПОВОДКОВОЮ СТРУКТУРНОЮ ГРУПОЮ ДРУГОГО ВИДУ( КРИВОШИПНО-ПОВЗУННИЙ МЕХАНІЗМ)

Механізм (рис. 9.3.).складається з початкової ланки 1 (кривошип) і двоповoдкової структурної групи 2 виду, яка включає ланки 2 (шатун) і 3 (повзун).

Рівняння замкненого векторного контуру механізму:

. (49)

Проектуючи рівняння (4.34) на осі координат, отримуємо систему алгебраїчних рівнянь:

; (50)

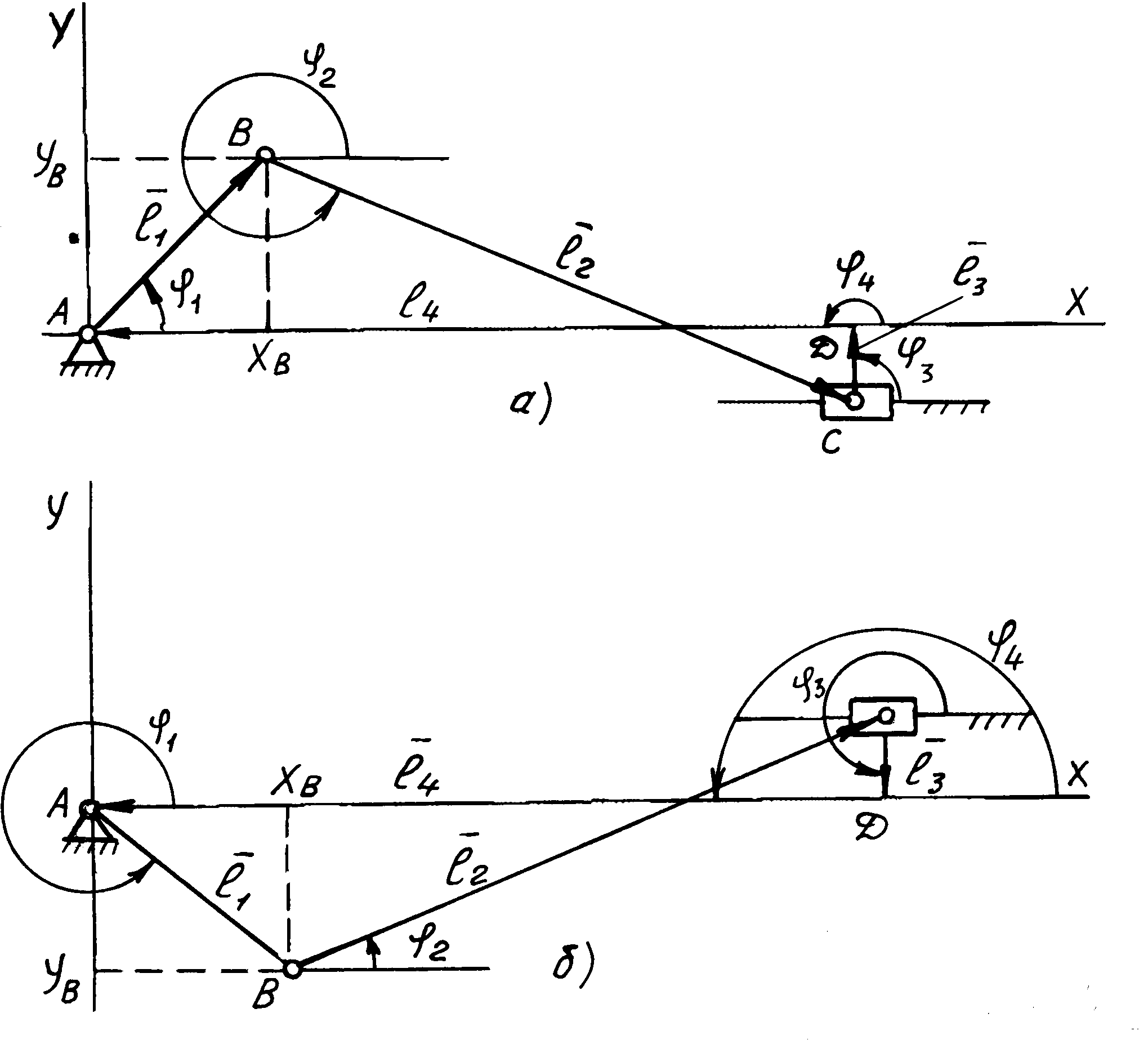
Рис. 9.3. Схема кривошипно-повзунного механізму.

Кути 1 вимірюються від позитивного напрямку осі АХ до позитивного напрямку відповідного вектора проти годинникової стрілки.

Для схеми (рис. 4.3,а) 3 = 90, 4 = 180; для схеми (рис. 4.3,б) 3 = 270,

4 = 180, тоді система рівнянь (51) матиме вигляд:

;

. (51)

Координати точки В:

; (52)

Для визначення координат точки С попередньо запишемо значення кута 2:

, (53)

тоді:

; (54)

Для визначення швидкостей, кутової ланки 2, та лінійної точки С диференціюємо систему рівнянь (51) по узагальненій координаті 1:

; (55)

Позначимо: ,

де - аналоги кутової та лінійної швидкостей відповідно 2 та 3 ланок. Тоді система (55) матиме вигляд:

; (56)

. (57)

З рівняння (57) визначаємо:

, (58)

а з рівняння (56):

. (59)

Аналогічно залежностям (36, 37) маємо:

; (60)

Тоді кутова швидкість другої ланки

. (61)

Лінійна швидкість точки С третьої ланки:

. (62)

Для визначення лінійного прискорення точки С і кутового прискорення другої ланки продиференціюємо рівняння (56, 57) по узагальненій координаті 1:

(63)

Позначимо і перепишемо систему (4.48):

; (64)

(65)

З рівняння (4.50) визначаємо :

, (66)

. (67)

Аналогічно залежностям (4.31, 4.33) кутове прискорення другої ланки:

. (68)

Лінійне прискорення точки С другої ланки:

. (69)

4. КУЛІСНИЙ МЕХАНІЗМ

Кулісний механізм (рис. 4.5) складається з вхідної ланки 1, яка утворює обертальну кінематичну пару з кулісним каменем 2. Кулісний камінь утворює поступальну кінематичну пару з кулісою 3. Вхідна ланка 1 і куліса 3 з’єднані зі стояком обертальними кінематичними парами А, С.

Розглянемо кулісний механізм у вигляді замкненого векторного контуру АВС, вектори якого утворені ланками 1, 2, 3.

Рівняння замкненого векторного контуру:

. (70)

Cпроектувавши рівняння (4.55) на координатні осі YСХ, одержуємо систему алгебраїчних рівнянь:

; (71)

. (72)

Для визначення напрямного кута 3 розділимо рівняння (72) на (71), тоді маємо:

. (73)

Визначимо довжину третьої ланки (куліси):

. (74)

Для визначення швидкостей ланок механізму диференціюємо систему (71-72) по узагальненій координаті 1:

; (75)

. (76)

Позначимо ,

де - аналог швидкості точки B3 відносно В2;

- аналог кутової швидкості ланки 3.

Рис. 4.5. Схема кулісного механізму.

Для визначення аналогів швидкостей від кутів, які входять в рівняння (75, 76) віднімаємо кут 3, що еквівалентно повороту системи координат на такий самий кут:

;

Аналогічно залежностям (62, 63) маємо:

(77)

(78)

Для визначення аналогів кутових і лінійних прискорень ланок і точок механізму рівняння (75, 76), з урахуванням прийнятих позначень, диференціюємо по узагальненій координаті 1:

(79)

(80)

де, - аналог кутового прискорення ланки 3;

- аналог лінійного прискорення точки B3 відносно B2.

Віднімаємо від кутів, які входять в рівняння (79, 80) загальний кут 3:

; (81)

, (82)

звідки:

;

Аналогічно залежності (69) визначаємо відносне (релятивне) прискорення :

. (83)

Прискорення Коріоліса визначаємо за формулою:

. (84)

Кутове прискорення третьої ланки визначимо з рівняння (82):

. (85)

Тоді лінійне прискорення точки В3 визначимо аналогічно (48):

(86)

PAGE 3

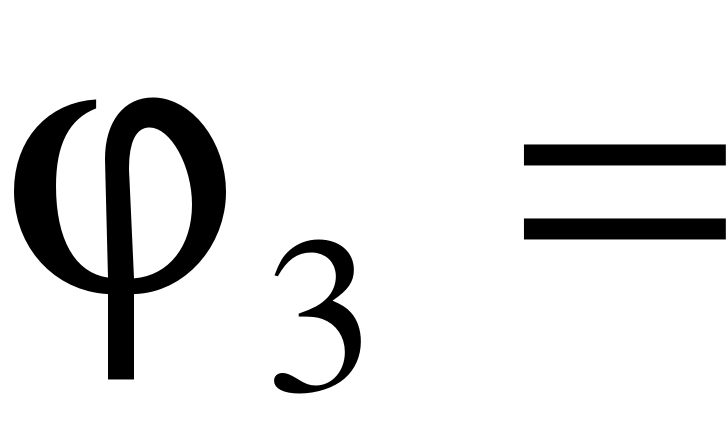
EMBED Equation.3

(5)

EMBED Equation.3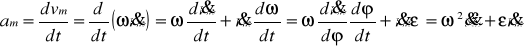

АНАЛІТИЧНІ МЕТОДИ КІНЕМАТИЧНОГО ДОСЛІДЖЕННЯ МЕХАНІЗМІВ