ВИЗНАЧЕННЯ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ ГРУП 3-го КЛАСУ МЕТОДОМ ПЛАНІВ

ЛЕКЦІЯ N9.

1. ВИЗНАЧЕННЯ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ ГРУП 3-го КЛАСУ МЕТОДОМ ПЛАНІВ.

1.1. Визначення лінійних і кутових швидкостей.

Визначення швидкостей і прискорень груп 3 класи може бути виконане так званим методом особливих Ассура, на ім'я російського вченого Ассура, що запропонував цей метод.

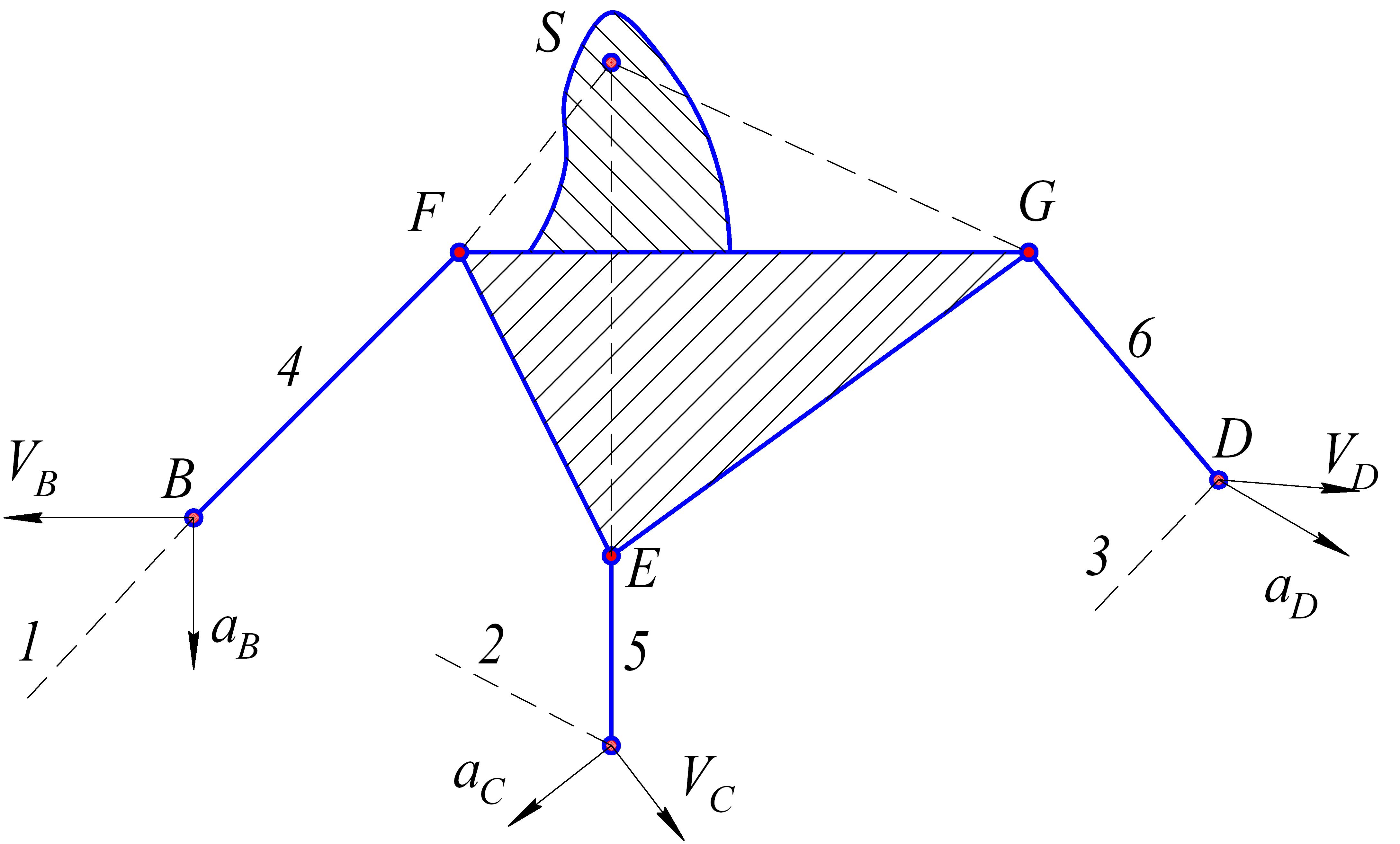
Розглянемо структурну групу 3-го класу з 3 повідцями (рис.1). Всі кінематичні пари, що входять до групи - обертальні. Задані швидкості і прискорення точок В, С, D кінцевих елементів.

Ми бачимо, що використовувати метод кінематичного аналізу груп 2-го класу в даному випадку неможливо, оскільки немає жодної точки групи, швидкість і прискорення якої можна було б визначити з двох відомих. Тому визначаємо положення особливих точок Ассура, для чого продовжимо осі повідців 1, 2 до перетину в точці S, яку приймемо такою, що належить базисній ланці 4.

Всього може бути визначено 3 точки Ассура, проте для вирішення поставленої задачі достатньо однієї. Крім того, необхідно орієнтувати повідці 1, 2, 3 так, щоб вони не перетиналися в одній точці S.

Визначимо швидкість точки S, як такої, що належить ланці 4 через точки F, E, які потім виразимо через відомі точки В, С. Для цього запишемо систему векторних рівнянь:

(1)

(2)

Два останні вектори рівнянь (1,2) направлені по одній прямій, оскільки обидва вектори перпендикулярні напрямам SB або SC.

Будуємо план швидкостей (рис.2) в довільному масштабі, для чого з точки р як з полюса, проводимо у вибраному масштабі вектори швидкостей точок В, C, D. Відповідно векторному рівнянню (1) з точки (b) проводимо пряму перпендикулярну BS, а відповідно рівнянню (2) з точки (c) проводимо пряму перпендикулярну CS.

Знайдена точка перетину цих прямих і визначає кінець вектора швидкості точки S. Сполучаємо точки S з полюсом і визначаємо величину швидкості точки S:

(3)

Наступною точкою, швидкість якої можна визначити, є точка G (через точку D, S, оскільки точка S приєднана до ланки 4). Запишемо систему рівнянь для визначення швидкості точки G:

(4)

(5)

Рис. 1.

Відповідно до рівняння (4) з точки S проводимо перпендикуляр до напряму SG, далі, відповідно рівнянню (5) з точки (d) проводимо перпендикуляр до ланки GD. Точка перетину цих прямих і є шуканою точкою (g)

Складемо систему векторних рівнянь для визначення швидкості точки Е:

(6)

(7)

Для визначення точки (е) на плані швидкостей відповідно до рівнянь (6), (7) з точки (f) проводимо пряму перпендикулярну FE, а з точки (g) - пряму перпендикулярну EG.

Положення точки (f) можна визначити використовуючи властивість подібності для базисної ланки 4. Трикутник fge плану швидкостей повинен бути подібний і відповідно розташований трикутнику FGE групи.

Абсолютні швидкості точок F, E, G визначаємо за формулами:

(8)

(9)

(10)

Кутові швидкості ланок визначаємо аналогічно групам 2-го класу. Для визначення кутової швидкості ланки 3 необхідне значення швидкості точки G відносно D і розділити її на довжину ланки 3:

(11)

Напрям кутової швидкості ланки 3 визначаємо паралельним перенесенням вектора відносної швидкості в досліджувану точку.

Аналогічно визначаємо кутові швидкості решти ланок.

1.2. Визначення лінійних і кутових прискорень.

Переходимо до визначення прискорень групи 3-го класу. Задача розв'язується аналогічно задачі про швидкості. Вибираємо довільну точку за полюс плану прискорень (рис. 3) і відкладаємо відрізки (b), (с), (d) що зображують в масштабі прискорення відповідних точок.

Спочатку визначаємо прискорення особливої точки Ассура S відносно С, В, прискорення яких відомі. Запишемо систему рівнянь, для точки S:

(12)

(13)

В рівнянні (12) вектор нормального прискорення точки S відносно точки F і вектор нормального прискорення точки F відносно точки В мають один і той же напрям (паралельно SB, від точки S до точки В). Аналогічно мають один і той же напрям вектори нормальних прискорень рівняння (13) (паралельно SC, від точки S до точки С).

Вектори тангенціальних прискорень перпендикулярні нормальним, тому також мають однаковий напрям. Вектори, що мають однаковий напрям об'єднуємо одним знаком вектора.

Величини нормальних відносних прискорень визначаємо звичайним методом з рівнянь:(14) (15) (16) (17)

У відповідності з (12) з точки b проводимо вектор (bn1) нормального

прискорення точки F відносно В паралельно SB в напрямі від S до В, далі з

Рис.3.

точки n1 проводимо вектор (n1n2) нормального прискорення точки S відносно F в тому ж напрямі.

Напрям тангенціальних складових прискорень проводимо з точки n2 перпендикулярно SB.

Аналогічно з точки с плану прискорень проводимо вектори (cn3) і (n3n4) нормальних прискорення точок Е відносно С і S відносно Е. Напрям тангенціальних складових проводимо з точки n4 перпендикулярно SC.

Точка перетину напрямів тангенціальних складових і буде шуканою точкою S плану прискорень.

Абсолютне прискорення точки S визначимо за формулою:

(18)

де (s) - довжина вектора прискорення точки S.

Прискорення точки G визначимо з наступної системи векторних рівнянь в які в якості початкових (відомих) точок приймаємо точки S і D.

(19)

(20)

В рівнянні (19) вектор нормального прискорення точки G відносно S направлений від точки G до точки S паралельно GS. Величину нормального прискорення визначаємо за формулою

(21)

Довжину відрізка (sn5) на плані визначаємо відповідно масштабному коефіцієнту плану прискорень:

(22)

В рівнянні (20) вектор нормального прискорення точки G відносно точки D направлений від точки G до точки D паралельно GD. Величину нормального прискорення визначаємо за формулою:

(23)

Довжину відрізка (dn6) на плані визначаємо аналогічно (22):

(24)

З точки S проводимо паралельно GS відрізок (sn5), що є в масштабі вектором нормального прискорення точки G відносно S. Далі з точки n5 проводимо пряму перпендикулярну GS, а, отже і відрізку (sn5 ), тобто напрям дії тангенціальної складової прискорення точки G відносно S. На цьому векторне рівняння (19) реалізовано повністю.

Переходимо до реалізації векторного рівняння (20). З точки d проводимо паралельно GD відрізок (sn6), що є в масштабі вектором нормального прискорення точки G відносно точки D і далі з точки n6 проводимо пряму перпендикулярну GD до перетину з прямою проведеною з точки n5. Точка перетину цих прямих є шукана точка g, що є закінченням вектора (g) прискорення точки G.

Абсолютне прискорення точки G визначаємо за формулою:

(25)

Далі складаємо систему векторних рівнянь для визначення прискорення точки F.

(26)

(27)

Прискорення точки F визначаємо з двох точок, прискорення яких відомі, тобто точок G і B.

Визначаємо значення нормальних складових прискорень аналогічно формулам (21) (23).

; (28)

. (29)

Довжини відрізків цих векторів, які зображають на плані прискорень:

; (30)

. (31)

Орієнтацію векторів визначаємо аналогічно раніше розглянутій точці G.

З точки G паралельно FG в напрямі від F до G проводимо відрізок (еn7) і далі з точки n7 проводимо лінію дії тангенціальної складової (перпендикулярно FG).

З точки b маємо вже проведений відрізок (bn1), в напрямі від точки F до точки B паралельно FB і далі з точки n1 проводимо лінію дії тангенціальної складової прискорення точки F відносно B (перпендикулярно FВ).

Точка перетину прямих є шуканою точкою f. Сполучаємо точку f з полюсом плану прискорень . Тоді абсолютне прискорення точки F визначаємо за формулою:

(32)

Точку e плану прискорень можна визначити двома способами:

1) використовуючи метод векторних рівнянь через дві відомі точки, наприклад F і G;

2) використовуючи властивість подібності фігури плану прискорень і фігури базисної ланки FGE.

Реалізуємо другий спосіб. Використовуючи відрізок (fg) побудуємо трикутник fge подібний і відповідно розташований трикутнику FGE базисної ланки 4 групи Ассура. Відповідність розташування точок перевіряється послідовним обходом контура, наприклад за годинниковою стрілкою. При цьому повинна зберігатися така ж послідовність точок.

Сполучаємо точку e з полюсом , відрізок (e) в масштабі є абсолютним прискоренням точки E, величину якого визначаємо за формулою:

(33)

Розглянемо приклад.

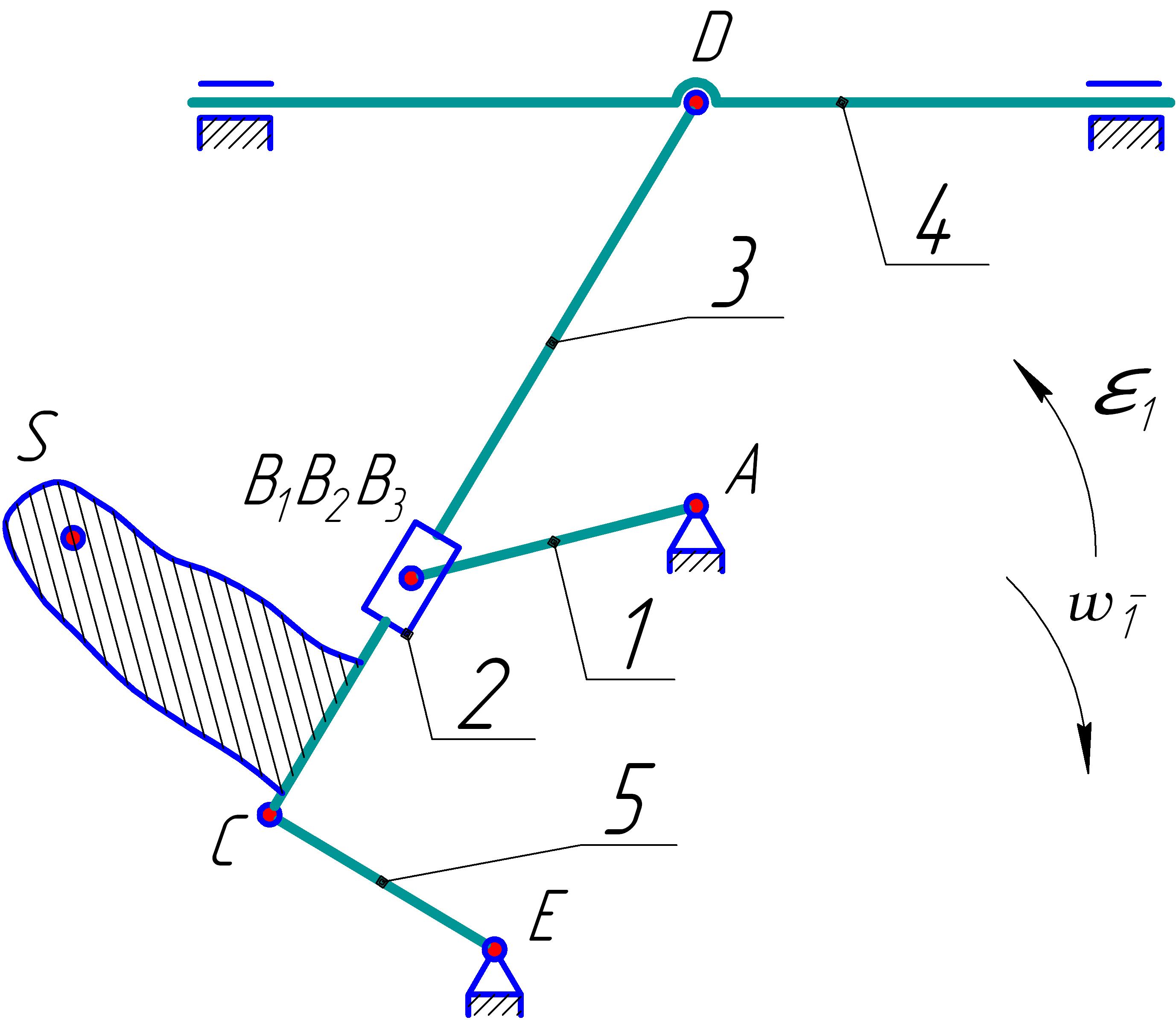
На рис. 4 зображена схема механізму 3-го класу з підвісною кулісою. Механізм включає кривошип 1, сполучений обертальною парою з кулісним каменем 2, який за допомогою поступальної КП сполучений з кулісою 3. Куліса 3 за допомогою обертальних кінематичних пар сполучена з одного боку з коромислом 4, а з іншою - з повзуном 5.

Механізм утворений приєднанням до початкової ланки 1 і стояку 0 (механізму 1-го класу) трьохповодкової структурної групи Ассура 3-го класу, що включає ланки 2,3,4,5.

Початкові дані: кутова швидкість кривошипа w1=const, задані також довжини всіх ланок механізму.

Ланка 1 (кривошип) є початковою, вхідним оскільки заданий закон його руху, ланка 5 (повзун) - вихідне.

Необхідно визначити лінійні швидкості і прискорення всіх точок і кутові швидкості і прискорення ланок механізму.

Ступінь рухливості механізму визначаємо за формулою Чебишева рис.4.

(34)

Практична степінь свободи (з геометричних уявлень)

Для даного механізму очевидно нерівність: , отже механізм містить надлишкові зв'язки, кількість яких:

. (35)

Таким локальним надмірним зв'язком є поступальна кінематична пара F', що дублює пару F. Тому для подальшого кінематичного дослідження виключаємо надлишковий зв'язок (дублюючу кінематичну пару F').

Необхідно зважати на те, що пару F' виключаємо лише теоретично для спрощення аналізу механізму. На практиці пара F' забезпечує повзуну 5 необхідну жорсткість і міцність, але при цьому вимагає підвищеної точності виготовлення механізму.

Далі визначаємо на базисній ланці 3 особливі точки Ассура. Вони знаходяться на перетині осьових ліній повідців або перпендикулярів до осей повзунів.

Для даного механізму раціонально вибрати точку Ассура S що знаходиться на перетині осьової лінії повідця 4 і перпендикуляра до куліси, проведеного через центр поступальної пари В.

Порядок дослідження механізму наступний:

1. Визначаємо швидкість точки В1,2

2. Далі складаємо систему векторних рівнянь для визначення швидкості особливої точки S, для чого розглядаємо точку S відносно точки С, а точку С - відносно Е. Аналогічно, з іншої сторони, розглядаємо рух точки S відносно точки В3, а В3 ,в свою чергу, відносно В1,2

3. Наступним кроком буде дослідження точки D відносно S з однієї сторони і точки D відносно D0 (стояка) – з іншої сторони.

4. Далі маємо можливість дослідити точку С відносно двох вже відомих точок Е і D.

5.Наостанку досліджуємо точку В3 через відомі точки С і D (за правилом подібності).

Рис. 2.

ВИЗНАЧЕННЯ ШВИДКОСТЕЙ І ПРИСКОРЕНЬ ГРУП 3-го КЛАСУ МЕТОДОМ ПЛАНІВ