Зачеплення Новикова

Лекція 28

1. Зачеплення Новикова

Евольвентне зачеплення, що завдяки своїм перевагам надзвичайно широко використовується у техніці, має, проте, деякі недоліки: а) малі зведені радіуси кривизни робочих поверхонь; б) підвищену через лінійний контакт зубів чутливість до перекосів; в) втрати енергії на тертя у зачепленні в результаті наявності відносного ковзання профілів. Ці недоліки зменшені у зачепленні Новикова.

Принципова можливість такого зачеплення випливає з формули коефіцієнта перекриття для косозубої передачі , згідно з якою коефіцієнт перекриття є сумою коефіцієнта перекриття у поперечному перетині (торцевого коефіцієнта перекриття ) і коефіцієнта перекриття від нахилу зубів (осьового коефіцієнта перекриття ), тобто

(1)

У прямозубій передачі з осьовим коефіцієнтом перекриття = 0 перекриття досягається за рахунок коефіцієнта . Логічний також інший випадок, коли = 0, а > 1, тобто = .

(2)

Це досягається, як видно з формули

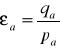
відповідним вибором робочої ширини зубчастих коліс і кутом нахилу зубів . Але, якщо = 0, то з формули

випливає, що довжина активної лінії зачеплення , тобто вона зникає і перетворюється в точку, яка в торцевому перетині не змінює свого

положення і переміщується вздовж лінії зубів. Тоді форма профілів зубів більше не зв'язує основну теорему зачеплення, і їх можна вибрати довільніше, керуючись лише міркуваннями міцності та довговічності. Таке зачеплення нового типу в 1955 р. запропонував радянський учений М. Л. Новиков. Він показав можливість використання цього зачеплення як для зубчастих коліс з паралельними осями (рис.1,а), так і для зубчастих коліс, осі яких перетинаються або схрещуються (рис. 1, в).

Отже, в зачепленні Новикова відсутня площина зачеплення, оскільки лінія Н1Н2 = 0 , залишається лише лінія зачеплення, паралельна осям коліс (для циліндричних коліс); перекриття досягається лише за рахунок нахилу зубів, тобто таке зачеплення не може бути прямозубим. Замість лінії контакту зубів маємо точку контакту. Через це зачеплення Новикова називають ще точковим зачепленням, або, враховуючи форму зубів, круглогвинтовим. Взагалі профілі зубів зачеплення Новикова можуть бути утворені різними кривими. Найпростішими, як показали дослідження, є профілі, окреслені у торцевому перетині дугами кола. Як правило, зуби одного колеса (частіше всього шестірні) мають випуклий профіль, а зуби іншого (більшого) колеса — увігнутий (рис.1, а, б).Побудова профілів зубів здійснюється у такому порядку (рис.1, б). За заданими міжосьовою відстанню, і передаточним відношенням u12 =z2 /z1 визначаємо радіуси початкових кіл rw1 і rw2. Проводимо через полюс П пряму N-N, що утворює з прямою t - t ,, перпендикулярною до лінії центрів, кут зачеплення аw. Випуклі профілі зубів меншого колеса викреслюються з центра, що збігається з полюсом П, дугою кола радіуса , де т, — модуль зачеплення у торцевому перетині. Угнуті профілі зубів більшого колеса викреслюються дугою кола радіуса з точки М, яка також міститься на прямій N—N. При малій різниці радіусів р, і р2 профілі зубів на деякій їх частині майже збігаються, що, не зважаючи на теоретичний точковий контакт, дає можливість створити значну площу контакту і тим самим зменшити контактні напруження у зубчастому зачепленні. Радіус ra2 кола вершин більшого колеса дорівнює радіусу rw2 початкового кола цього колеса. Радіус кола вершин меншого колеса. (9.83)

Радіус кола западин меншого колеса

Товщину зуба одного з коліс можна вибрати довільно, а товщину другого визначають побудовою, і вони пов'язані між собою умовою s1 = (1,3 . . 1,5)s2; сума s1 +s2 дещо менша від кроку р. При проектуванні зачеплення Новикова рекомендується кут зачеплення , кут нахилу зубів .

Оскільки зубці стикаються в одній точці, висота їх теоретично може дорівнювати нулю; практично ж вона може бути невеликою, що сприяє міцності зубів на згин.

Розглянута передача має одну лінію зачеплення і її несуча здатність приблизно у 1,5 рази більша, ніж у евольвентної косозубої передачі. Якщо головки зубів обох коліс виконати випуклими, а ніжки увігнутими, матимемо передачу Новикова з двома лініями зачеплення, у якої зуби стикаються у двох точках (на ніжці й головці), зміщених відносно одна одної. Несуча здатність такої передачі вища, ніж передачі з однією лінією зачеплення, а шум менший.

Для нарізання випуклих та угнутих зубів необхідно мати різний інструмент. Зуби передач із двома лініями зачеплення нарізаються одним інструментом. На рис. 9.36 наведено вихідні контури для нарізання зачеплення: а) з однією лінією зачеплення; б) із двома лініями зачеплення. Останнім часом ширше використовують передачі Новикова з двома лініями зачеплення, проте такі передачі чутливіші до перекосу осей.

Отже, передача Новикова завдяки меншим контактним напруженням і згинальним моментам мають в 1,5—2 рази вищу несучу здатність, ніж аналогічні евольвентні передачі, і завдяки кращим умовам змащення, меншому відносному ковзанню мають дещо вищий ККД. У зв'язку з тим що мінімальне число зубів шестерні може бути малим (теоретично може дорівнювати навіть одиниці), такі передачі дають змогу забезпечувати високі передаточні відношення.

До недоліків зачеплення Новикова треба віднести: 1) складніший різальний інструмент, для кожної пари зубів коліс треба мати свій комплект фрез; 2) нижчий коефіцієнт перекриття, оскільки = 0; 3) для забезпечення високого коефіцієнта треба брати широкі зубчасті колеса. Незважаючи на ці недоліки, зачеплення Новикова одержало досить широке розповсюдження, особливо в редукторах загального призначення, кораблебудуванні та в інших галузях машинобудування.

2.ПРОСТОРОВІ ЗУБЧАСТІ ПЕРЕДАЧІ У багатьох машинах для забезпечення роботи механізмів необхідно передавати обертовий рух з одного вала на інший за умови, що осі цих валів або перетинаються, або схрещуються. У таких випадках використовують просторові зубчасті механізми, до яких належать конічні зубчасті передачі або різновиди гіперболоїдних зубчастих передач (гвинтові зубчасті передачі, черв'ячні, гіпоїдні).

10.1. Конічні зубчасті передачі

Конічні зубчасті колеса, як і конічні фрикційні котки, застосовуються для передачі обертового руху між валами, осі яких перетинаються. Міжосьовий кут (рис.2) визначається конструктивною необхідністю і може змінюватись у межах 10—170°. Найчастіше зустрічаються конічні передачі при перетині осей під кутом = 90°. Такі конічні передачі називають ортогональними.

Конічну зубчасту передачу (рис. 2, а) можна уявити собі як передачу двома конічними котками, на поверхні яких для усунення проковзування нарізані зубці. Аксоїдами у відносному русі таких коліс є два конуси з кутами конусності і які в сумі дорівнюють міжосьовому куту.

За аналогією з циліндричними зубчастими передачами ці конуси називають початковими, оскільки вони перекочуються один по одному без ковзання, а кути w1і w2 — кутами початкових конусів конічних коліс. На практиці найчастіше використовують конічні колеса без зміщення. Тоді початкові та ділильні конуси збігаються, а кути початкових конусів дорівнюють кутам ділильних конусів (w1= 1, w2= 2).

Передаточне відношення конічної передачі u12 визначається

з припущення, що початкові конуси котяться один по одному без ковзання. При цьому швидкості точок стикання, що належать обом конусам (рис. 2, а), будуть дорівнювати одна одній. Наприклад, для точки П можна записати

vП1 =vП2 = 1П1О= 2П2О;

де П1, П2 — точки, що належать відповідно шестерні та колесу і в даний момент збігаються з точкою П.

Тоді передаточне відношення можна виразити через радіуси початкових кіл або числа зубів (нагадуємо, що ми прийняли

rw1= ri=mzi/2):

(10.2)

У формулі (10.2) rw1 =П1О'; rw2 =П2О'' - радіуси початкових кіл шестірні й колеса в точці П.

Розглядаючи трикутники ОПО' і ОПО" , можна записати

Для ортогональних конічних передач залежність (10.3) має вигляд

(Ю.4)

Профілі зубів конічних коліс утворюються прямою ОА площини N, яка обкочується без ковзання по основному конусу (рис. 10.1, б). При цьому будь-яка точка Аi, прямої ОА описує евольвенту АiBі, а пряма ОА - - евольвентну поверхню, яка вибирається головною бічною поверхнею конічного зубчастого колеса.

У прямозубих колесах лінія ОА збігається з твірною основного конуса. Але, враховуючи те, що в довільному положенні кожна точка евольвенти, наприклад АВ, завжди знаходиться на однаковій відстані ОА від вершини основного конуса О, то профілі зубів спряжених конічних коліс треба будувати на сферичних поверхнях з центром у точці О (рис. ІО.І, в). Проте профілювання та виконання евольвентного конічного зачеплення пов'язані і цілим рядом труднощів, оскільки сферична поверхня точно не розгортаєгься на площину. На практиці при побудові профілів зубів сферичні поверхні замінюють конічними, точна розгортка яких легко будується на площині. Оскільки висота зуба конічного колеса незначна порівняно з радіусом Re сфери, то неточність, що виникає від заміни сферичної поверхні конічною, досить невелика. Таким чином, складна задача побудови профілів на сферичній поверхні зводиться до наближеного, але простого графічного розв'язання цієї задачі на площині. Але перш ніж приступити до цього питання, розглянемо деякі інші особливості геометрії конічних передач.

На рис. 10.1, г зображено пару конічних зубчастих коліс, які
перебувають у зачепленні. В таких передачах, за аналогією з
циліндричними, розглядають, крім основних, початкових і
ділильних конусів, про які вже говорилось раніше, ще конуси
вершин і западин (аi- кут конуса вершин, - fi кут конуса западин). Як торцеві перетини розглядають перетини зубчастого
колеса поверхнями додаткових конусів, тобто конусів, осі яких
збігаються з осями коліс, та їх твірні, перпендикулярні до
твірних ділильною конуса. Відрізняють зовнішній і внутрішній
додаткові конуси, шо обмежують зубчастий вінець і визначають
ширину зубчастого вінця b та середній додатковий конус, твірна
якого ділить ширину зубчастого вінця b на дві рівні частини.

Конічні зубчасті передачі у виготовленні та монтажі складніші, ніж циліндричні. Для нарізання коліс потрібні спеціальні верстати й інструмент. Перетин осей валів утруднює розміщення опор. При Цьому одне з конічних коліс, як правило, розташоване консольні)цю приводить до збільшення нерівномірності розподілу

В конічному зачепленні діють значні осьові сили, що ускладнює конструкцію опор валів. Все це приводить до того, що несуча здатність конічної передачі становить лише близько 0,85 % порівняно з циліндричною.

Але, незважаючи на вказані недоліки, конічні передачі досить широко використовуються в техніці, оскільки в конструкціях машин, приладів необхідно розташовувати вали під кутом.

10.2. Гвинтові зубчасті передачі

Механізми гвинтових зубчастих коліс (рис. 4) застосовують у тих випадках, коли треба передавати обертання між осями, що схрещуються (осі не паралельні і не перетинаються), із сталим передаточним відношенням:

Такі передачі є окремим випадком гіперболоїдних зубчастих передач. Початковими поверхнями гвинтової передачі є два кругових циліндри, які дотикаються в точці, що лежить на лінії найкоротшої відстані між осями коліс.

На рис. 4 показано проекції двох початкових циліндрів гвинтових зубчастих коліс 1 і 2, бічні поверхні профілів зубів яких дотикаються одна до одної в точці П. При цьому один циліндр перекочуватиметься по другому, ковзаючи вздовж миттєвої осі обертання і ковзання. Осі 1—1 і 2—2 початкових циліндрів схрещуються під кутом . Гвинтові колеса так само, як і косозубі циліндричні колеса, мають гвинтові зуби, нахилені до відповідних осей під кутами 1 і 2. У гвинтових колесах має справджуватись рівність

1 і 2= . (Ю.7)

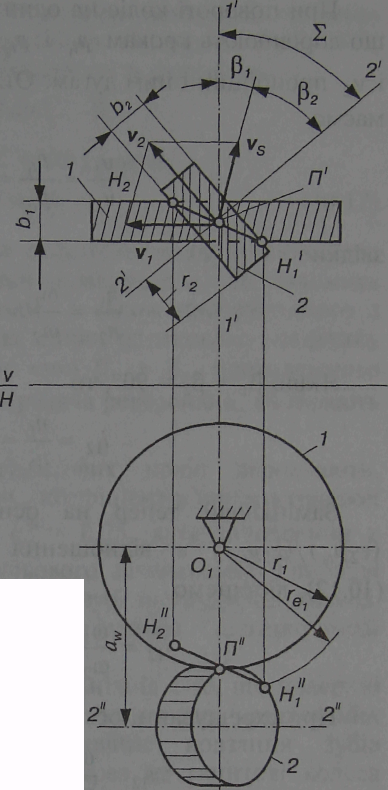
Кожне з гвинтових коліс у процесі нарізання має свою площину зачеплення. У спряжених гвинтових колесах ці площини перетинаються і утворюють лінію зачеплення H1H2, що проходить через точку П, а тому поверхні зубів цих коліс у процесі обертання весь час стикаються в точці, що переміщається по лінії H1H2.

З двох косозубих коліс можна скласти гвинтову передачу, якщо кожне з них має можливість спрягатися в зачепленні з одною й тою самою рейкою (в якої в середній площині товщина зубів дорівнює ширині западин). У цьому випадку косозубі колеса повинні мати однакові нормальні кроки та модулі.

Тоді, між торцевим кроком рt, і нормальним кроком рn для обох гвинтових коліс можна встановити такі залежності:

(10.8)

або

Встановимо тепер основні співвідношення між різними параметрами гвинтових коліс У зв'язку з тим, що гвинтова передача може вписатися в необхідну міжосьову відстань за рахунок вибору кутів нахилу зубів, а використання зміщених передач (хі 0) не дає значного поліпшення якісних показників зачеплення, доцільно використовувати незміщені гвинтові передачі, в яких початкові й ділильні циліндри збігаються. Позначимо радіуси цих циліндрів r1 і r2, числа зубів або витків- z1, z2 числа обертів коліс за хвилину –n1 і п2, а колові швидкості коліс на поверхнях початкових циліндрів – v1, і v2. Тоді дістанемо такі співвідношення:

2r1=z1pt1 i 2r2=z2pt2 (10.10)

При повороті коліс на один зуб ободи коліс проходять дуги, що дорівнюють крокам рt1 і рt2, а значить, колові швидкості v1,

і v2 пропорційні цим дугам. Отже, з врахуванням (10.8) і (10.11) маємо

При схрещуванні осей під прямим кутом маємо

Як видно з одержаних залежностей, передаточне відношення в гвинтових передачах залежить не тільки від діаметрів (радіусів) початкових циліндрів, а й від кутів нахилу зубів р! і Р2-Отже, пара гвинтових коліс при незмінних значеннях початкових діаметрів може мати різні передаточні відношення залежно від вибраних кутів р, і Р2. Вибираючи ці кути, намагаються звичайно забезпечити вищі ККД передачі.

Недоліком зубчастих гвинтових механізмів є те, що поверхні зубів стикаються в точці, а значить, контактні напруження будуть значними. Крім цього, подвійне ковзання зубів спричиняє їх швидке спрацювання. Через це гвинтові колеса можна використовувати лише при невеликих швидкостях і незначних потужностях як другорядні передачі в машинах.

2. Черв'ячні передачі

Для передачі руху між осями, що схрещуються, досить широке

поширення одержали черв'ячні передачі, які є різновидом передач гвинтовими колесами. Найчастіше використовуються ортогональні передачі (з кутом схрещення 2 = 90°). Якщо на одному з гвинтових коліс передачі зробити зуби під великим кутом, одержимо так званий черв'як, а на другому (під малим кутом) - черв'ячне колесо. Черв'як має форму одновиткового або багатовиткового гвинта (рис. 10.4). Черв'ячне колесо, яке з ним перебуває у зачепленні, має зуби, утворені як огинаючі

А-А

Рис. 10.4.

витки черв'яка. Черв'ячна передача в осьовому перетині А—А черв'яка, перпендикулярному до осі колеса, нагадує передачу шестерні з рейкою, а в осьовому перетині Б—Б колеса, перпендикулярному до осі черв'яка, — гвинтову передачу. Черв'ячне колесо можна собі уявити також як деякий сектор довгої гайки, обгорнутий навколо циліндричного тіла. Тому черв'ячна передача має властивості як зубчастої, так і гвинтової передач. Як відомо, робота останньої супроводжується значним відносним тертям ковзання витків гайки та гвинта.

Широке застосування черв'ячних передач пояснюється їх значними перевагами. Такі передачі:

забезпечують великі передаточні відношення, звичайно
/12 = 6—80, але можливі передачі (для приводу, наприклад,
поворотних столів металорізальних верстатів), в яких /І2 = 500 і
навіть /12 = 1000;

забезпечують безшумність у роботі та плавність зачеплення;

мають малі масу й габарити;

• мають можливість самогальмування (при низьких ККД).
Основні недоліки черв'ячних передач викликані наявністю

відносного ковзання витків черв'яка і зубів черв'ячного колеса.

PAGE 3

Зачеплення Новикова