Завдання механіки маніпуляторів. Кінематичний аналіз механізму маніпулятора. Динаміка маніпуляторів промислових роботів

ЛЕКЦІЯ 36

ПРОМИСЛОВІ РОБОТИ І МАНІПУЛЯТОРИ (ПРОДОВЖЕННЯ)

    Завдання механіки маніпуляторів. Кінематичний аналіз механізму маніпулятора. Динаміка маніпуляторів промислових роботів. Зрівноважування маніпуляторів. Кінетостатичний розрахунок маніпуляторів. Розрахунок швидкодії приводу.

Завдання механіки маніпуляторів.

    До основних завдань механіки маніпуляторів можна віднести:

  • розробку методів синтезу і аналізу виконавчих механізмів (включаючи механізми приводів);
  • програмування руху маніпулятора;
  • розрахунок зусиль, що управляють, і реакцій в КП;
  • зрівноважування механізмів маніпуляторів;
  • інші завдання.

Ці завдання вирішуються на базі загальних методів дослідження структури, геометрії, кінематики і динаміки систем з просторовими багаторухомими механізмами. Кожне з даних завдань може бути сформульована як пряма (завдання аналізу) або як зворотна (завдання синтезу). При визначенні функцій положення механізму, в прямому завданні знаходять закон зміни абсолютних координат вихідної ланки по заданих законах зміни відносних або абсолютних координат ланок. У зворотній - по заданому закону руху схвата знаходять закони зміни координат ланок, зазвичай, лінійних або кутових переміщень в приводах.

Рішення зворотної задачі або завдання синтезу складніше, оскільки часто вона має безліч допустимих рішень, з яких необхідно вибрати оптимальне. У зворотному завданні кінематики по необхідному закону зміни швидкостей і прискорень вихідної ланки визначаються відповідні закони зміни швидкостей і прискорень в приводах маніпулятора. Зворотне завдання динаміки полягає у визначенні закону зміни сил, що управляють, і моментів в приводах, що забезпечують заданий закон руху вихідної ланки.


Кінематичний аналіз механізму маніпулятора.

    Перше і основне завдання кінематики - визначення функції положення. Для просторових механізмів найбільш ефективними методами рішення цієї задачі є векторний метод і метод перетворення координат. При рішенні прямої задачі про положення схватe маніпулятора зазвичай використовують метод перетворення координат. З безлічі методів перетворення координат [ 1, 2 ], які відрізняються один від одного правилами вибору осей локальних систем координат, для маніпуляторів зазвичай використовується метод Денавіта і Хартенберга.

Опишемо два види матриць:

матриці  М, що визначають відношення між системами координат сусідніх ланок;
матриці Т, визначальне положення і орієнтацію кожної ланки механізму в нерухомій або базовій системі координат.

    Скористаємося однорідними координатами тривимірного проектного простору Рr3, в яких рух евклідів простір R3 можна представити лінійним перетворенням

 

де Мij - матриця 4x4 вигляду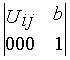

.

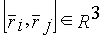
    Це перетворення еквівалентне перетворенню в евклідовому просторі 

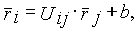
 де 

Тобто перетворенню, яке включає поворот, визначуваний матрицею Uij розмірністю 3х3, і паралельне перенесення, що задається вектором   розмірністю 3. У однорідному просторі положення точки визначатимуть не три x, у і z, а чотири величини x', у', z' і t', які задовольняють наступним співвідношенням:

x = x'/t', у = y'/t', z = z'/t'.

    Зазвичай приймають t'=1. У матриці повороту Uij елементами uij є направляючі косинуси кутів між новою віссю i і старою віссю j. Вектор

- тривимірний вектор, що визначає положення початку нової системи координат i в старій системі j. Вибір розташування осей повинен відповідати вирішуваному завданню. При рішенні задачі про положення необхідно: у прямому завданні визначити положення вихідної ланки як функцію переміщень в приводах, в зворотній - задане положення вихідної ланки представити як функцію переміщень в приводах. Вибір розташування і орієнтації локальних систем координат повинен забезпечувати виконання цих завдань. При використанні методу Денавіта і Хартенберга осі координат розташовуються по наступних правилах:

    1. Для ланки i вісь zi спрямовують по осі кінематичної пари, що утворюється з ланкою ( i+1). Початок координат розміщують в геометричному центрі цієї пари.

    2. Вісь xi прямує по загальному перпендикуляру до осей zi-1 і zi з напрямом від zi-1 до zi. Якщо осі zi-1 і zi збігаються, то xi перпендикулярна до них і направлена довільно. Якщо вони перетинаються в центрі кінематичної пари, то початок координат розташовується в точці перетину, а вісь xi спрямовують за правилом векторного добутку

(найкоротший поворот осі zi до поєднання з zi-1 при спостереженні з кінця xi повинен відбуватися проти годинникової стрілки).
    3. Вісь yi прямує так, щоб система координат була правою.

    У прямому завданні необхідно визначити положення схвата маніпулятора і пов'язаної з ним системи координат Mxnynzn по відношенню до нерухомої або базової системи координат Kx0y0z0. Це здійснюється послідовними переходами з системи координат ланки i в систему координат ланки i-1. Згідно прийнятому методу, кожен перехід включає послідовність чотирьох рухів: двох поворотів і двох паралельних перенесень, здійснюваних у вказаній послідовності (див. рис. 20.1):

  • поворот i-ї системи навколо осі xi на кут -qi до паралельності осей zi і zi-1 (позитивний напрям повороту при спостереженні з кінця вектора xi проти годинникової стрілки);
  • перенесення уздовж осі xi на величину -ai до поєднання почала системи координат Oi з точкою перетину осей xi і zi-1 (відлік по осі xi від точки перетину осі xi і осі zi-1);


Рис. 20.1.
  • перенесення уздовж осі zi-1 на величину -si, після якого початок системи координат Oi виявляється на початку координат Oi-1 системи (i-1) (відлічується по осі zi-1 від її початку координат Oi-1 до точки її перетину з віссю xi);
  • поворот навколо осі zi-1 на кут -ji, до тих пір, поки вісь xi не стане паралельній осі xi-1 (позитивний напрям повороту при спостереженні з кінця вектора zi-1проти годинникової стрілки).

    Необхідно відзначити, що знак кута повороту не має значення, оскільки в матрицях переходу використовуються направляючі косинуси (парні функції). Доцільно розглядати кут, що забезпечує найкоротший поворот осі старої системи i до поєднання (паралельності) з відповідною віссю новою ( i-1). Переміщення початку координат визначаються як координати початку старої системи Oi в новій Oi-1.

    У маніпуляторах зазвичай використовуються однорухомі кінематичні пари або обертальні, або поступальні. Обидва відносні рухи як обертальне, так і поступальне, реалізуються в циліндричних парах. Тому при загальному представленні механізму використовуються (рис.20.1) циліндричні пари.
    Матриці переходу їх системи Oi в систему Oi-1 можна записати так:

,

дде:

- матриця повороту навколо осі xi на кут i

- матриця перенесення уздовж осі xi на -ai

- матриця перенесення уздовж осі zi-1 на -si

- матриця повороту навколо осі zi-1 на кут -i.

    У цих матрицях змінні si і i відповідають відносним переміщенням ланок в кінематичних парах і є узагальненими координатами маніпулятора, що визначають конфігурацію механізму в даному положенні. Змінні ai і i визначаються конструктивним виконанням ланок маніпулятора, в процесі руху вони залишаються незмінними.

Положення деякої довільної точки М в системі координат ланки i визначається вектором rMi, а в системі координат ланки (i-1) - вектором rMi-1. Ці радіуси зв'язані між собою через матрицю перетворення координат Мi наступним рівнянням:

,

дде:

- матриця

переходу з i-ї системи координат в (i - 1)-у.

    Розглянемо шестирухомий маніпулятор в початковому або вихідному положенні (рис.20.2). За початкове положення береться таке, в якому всі відносні узагальнені координати дорівнюють нулю. Перехід з системи координат будь-якої i-ї ланки до нерухомої або базової системи записується у вигляді

 або 

Де    - матриця перетворення координат i-ї системи в координати базової системи координат.


Рис. 20.2

Для схеми, зображеної на рис.20.2, радіус rM6 = 0, а радіус rM0 визначиться по формулі

,

тобто положення вихідної ланки маніпулятора визначається матрицею Тn. Елементи цієї матриці визначають положення центру схвата точки М і орієнтацію його в просторі. Четвертий стовпець визначає, декартові координати точки М (проекції вектора rM0на осі координат). Третій стовпець містить направляючі косинуси осі zn системи координат, пов'язаної зі схватом, або вектора підходу , який характеризує напрям губок схвату (рис.20.3). Другий стовпець визначає напрям осі yn або вектора орієнтації, який проходить через центр схвату по осі перпендикулярній робочим поверхням його губок. У першому стовпці містяться направляючі косинуси осі xn або вектора   . Кутом підходу схвату   називається кут між вектором підходу   і базовим вектором

,

де   - орт вектора   нерухомої або базової системи координат. З урахуванням сказаного, матриця Tn может бути представлена в наступному вигляді


Рис. 20.3

    В результаті матричних перетворень отримуємо радіус-вектор точки М схвату у функції узагальнених координат. Зазвичай, за узагальнені координати приймають лінійні і кутові переміщення в кінематичних парах або на вихідних валах приводів маніпулятора. У механізмі з  рухомостями в загальному вигляді функцію положення схвату можна записати так

де q1, q2 ... qn - узагальнені координати маніпулятора.

    При кінематичному аналізі маніпулятора в прямому завданні необхідно визначити лінійні і кутові швидкості і прискорення схвату при заданих кутових і лінійних узагальнених швидкостях і прискореннях (зазвичай відносних швидкостях і прискореннях в кінематичних парах механізму). У зворотному завданні по заданому закону зміни швидкостей і прискорень схвату визначаються закони зміни швидкостей і прискорень в КП або на вихідних ланках приводів. Рішення прямої задачі кінематики для точки М схвату можна отримати продиференціювавши четвертий стовпець матриці Тn за часом

    Кутову швидкість і кутове прискорення схвату можна визначити векторним підсумовуванням відносних кутових швидкостей в обертальних КП механізму. Оскільки вектори кутових швидкостей, при даному виборі орієнтації осей координат, збігаються з віссю z, то кутова швидкість схвату

де   орт осі z системи координат, розташованої в центрі КП, що сполучає ланку i і ланку i-1, m - число обертальних КП в механізмі.

    Диференціюючи цей вираз за часом, отримаємо формулу для визначення кутового прискорення схвату:


Динаміка маніпуляторів промислових роботів.
Силовой розрахунок маніпулятора.

    З великої різноманітності завдань динаміки маніпуляторів розглянемо дві: силовий розрахунок і розрахунок швидкодії ПР. При силовому розрахунку маніпуляторів вирішується завдання за визначенням зовнішніх силових дій, що управляють, забезпечують необхідний закон руху механізму, і за розрахунком реакцій в кінематичних парах. Першу частину часто називають завданням синтезу управління . При силовому розрахунку зазвичай застосовується метод кінетостатики, заснований на принципі Д'аламбера. По цьому методу до зовнішніх сил і моментів, прикладених до ланок механізму, додаються розрахункові сили інерції, які забезпечують силову врівноваженість системи і дозволяють розглядати рухому систему в квазістатичній рівновазі, тобто, як умовно нерухому. Силовий розрахунок виконується при заданому корисному навантаженні, відомих законах руху ланок   і   (з попереднього кінематичного розрахунку), відомих інерційних характеристиках ланок: масах ланок mi і їх моментах інерції Isi. За цими даними визначаються головні вектора   і головні моменти   сил інерції для кожної з ланок механізму. Для відкритого кінематичного ланцюга рішення починаємо з вихідної ланки - схвату. Відкинуті зв'язки ланки n з ланкою n-1 і вихідним валом приводу ланки n замінюємо реакціями   і   і складаємо кинетостатичні векторні рівняння рівноваги сил і моментів для ланки n (рис.20.4):


де   - вектор моменту в кінематичній парі (проекція цього вектора на вісь z є рушійним моментом приводу в КП, тобто  ).


Рис. 20.4

    Проектуючи векторні рівняння на осі координат, отримаємо систему шести рівнянь алгебри звідки визначимо шість невідомих

    Далі розглядається рівновага ланки n-1. При цьому в місці її приєднання до ланки n прикладаються реакції з боку ланки n

, рівні по величині і протилежні по напряму реакціям, визначеним на попередньому етапі розрахунку. Так послідовно складаються рівняння силової рівноваги для всіх n ланок механізму. З вирішення отриманої системи 6n рівнянь визначаються реакції в кінематичних парах, рушійні сили і моменти.

Розрахунок швидкодії промислового робота.

    Час виконання роботом циклу переміщень деталі багато в чому визначає продуктивність всього роботизованого комплексу. Тому вимоги до швидкодії робота зазвичай достатньо високі. Час виконання роботом технологічної операції зумовлений законами зміни зовнішніх сил (рушійних і опору) і інертністю ланок механізму. Закон зміни сил, що управляють, залежить від типу використовуваного приводу і від виду системи управління. Існують роботи з гідравлічними, пневматичними, електричними і комбінованими приводами. У них застосовуються циклові, позиційні або контурні системи управління. Розглянемо розрахунок швидкодії однієї з приводів промислового робота з цикловою системою управління. При цикловій системі управління відносні переміщення ланок обмежуються пересувними упорами і кінцевими вимикачами.
    На рис. 20.5 зображена кінематична схема трирухомого маніпулятора ПР (1,2,3 - рухомі ланки, 0 - нерухома ланка). Тут же приведена циклограма налаштування командоаппарату (суцільні лінії) і циклограма роботи ПР (пунктирні лінії). Загальний час робочого циклу Тц складається з часу вистою в заданих положеннях (на циклограмі вистій показаний прямими паралельними горизонтальній осі t) і часу відносних переміщень ланок з одного заданого положення в інше tпх і назад tох (похилі прямі на діаграмах ). Час вистою зазвичай заданий умовами технологічного процесу. Час виконання роботом рухів визначається динамічними характеристиками приводів і маніпулятора - рушійними силами і силами опору, масами і моментами інерції ланок.

Циклограми командоаппарата і промислового робота.


Рис. 20.5

    Розглянемо роботу пневмоприводу переміщення руки маніпулятора (рис.20.5). По сигналу від командоапарату в праву порожнину циліндра подається стиснене повітря, яке діє на поршень з силою Fд3 = p*Sп, де р - тиск повітря, Sп - активна площа поршня. Під дією цієї сили поршень і рука 3 переміщуються вліво з постійним прискоренням і із зростаючою швидкістю V32 (рис.20.6а). Обмеження ходу поршня може здійснюватися або жорстким упором без демпфера, або упором з демпфером.


Рис. 20.6

    При зупинці на упорі без демпфера, швидкість ланки 3 мусить миттєво зменшиться з деякого кінцевого значення до нуля. При такій зміні швидкості прискорення a32 прямує до нескінченності. Така зупинка ланки називається жорстким ударом. Вона супроводжується великими динамічними навантаженнями на ланки механізму. Оскільки реальний маніпулятор є пружно-інерційною системою, то ці навантаження викличуть відскакування ланки 3 від упору, а також коливання всього механізму. Схват здійснюватиме коливання відносно заданого кінцевого положення. Час загасання цього процесу Dt (рис.20.6а) значно знижує швидкодію ПР.
    Зменшити ці коливання або взагалі виключити їх можна, забезпечивши безударний останов

V32n = 0,    a32n = 0;

де V32n, a32n - відносна швидкість і відносне прискорення ланок у момент останову. Проте це здійсненно тільки в регульованому приводі при контурному управлінні. Крім того при безударному останові в кінці ходу відносна швидкість близька до нуля, тому час переміщення схвату в необхідне положення значно зростає. Компромісним рішенням є останов з м'яким ударом, при якому відносна швидкість в кінці ходу V32n= 0, а прискорення обмежене деяким допустимим значенням a32n <= [a] . У механізмах з цикловим управлінням режим руху з м'яким ударом забезпечується установкою упорів з демпферами, що гасять кінетичну енергію руки. Розрахунок демпфера ведеться з умови An =0 , яке забезпечується рівністю за цикл руху роботи рушійної сили AFд3 і роботи сили опору демпфера Аfc (рис. 20.6б):

AFд3 = -АFc     або     Fд3 * (H32 - hд) = - Fc * hд.

У цьому виразі невідомі дві величини Fc і hд, однією з них задаються, другу - розраховують.

Зрівноважування маніпуляторів.

    У більшості кінематичних схем маніпуляторів приводи сприймають статичні навантаження від ваги ланок. Це вимагає значного збільшення потужностей двигунів приводів і моментів гальмівних пристроїв. Для боротьби з цим використовують три методи:

  • Використовують кінематичні схеми маніпуляторів, в яких сили тяжіння ланок сприймаються підшипниками кінематичних пар. На потужність приводів і гальмівних пристроїв при такому вирішенні сили тяжіння роблять вплив тільки через сили тертя в парах. Як приклад можна привести кінематичну схема робота SCARA (рис. 20.7). Недоліком цього методу є великі осьові навантаження в підшипниках.


Рис. 20.7

  • Зрівноважування ланок маніпулятора за допомогою корегування їх маси. При цьому центр мас ланки за допомогою мас, що коректують, зміщується в центр кінематичної пари ( рис. 20.8 ). Недоліком цього методу є значне збільшення маси маніпулятора і моментів інерції його ланок.


Рис. 20.8

  • Урівноваження сил ваги ланок маніпулятора за допомогою пружних розвантажуючих пристроїв - пружинних розвантажувачів або уравновешивателей. Ці пристрої не дозволяють забезпечити повне розвантаження приводів від дії сил ваги на всьому відносному переміщенні ланок. Тому конструкція цих пристроїв включає кулачкові або важелі механізми, які погоджують пружну характеристику пружини з характеристикою врівноважуваних сил ваги ланок. На рис. 20.9 показана схема примышленного робота в якому привід вертикального переміщення руки забезпечений механізмом для силового розвантаження, що складається з пружини і кулачкового механізму з профілем виконаним по спіралі Архимеда.


Рис. 20.9


Точність маніпуляторів Ін.

    Точність маніпуляторів визначається погрішностями позиціонування характеристичної точки схвата (точка М) і погрішностями кутової орієнтації схвата. Погрішності позиціонування визначаються технологічними відхиленнями розмірів ланок маніпулятора, зазорами в кінематичних парах маніпулятора і механізмів приводів, деформаціями (пружними і температурними) ланок, а також погрішностями системи управління і датчиків зворотного зв'язку. У паспортних даних маніпуляторів указується максимально допустиме відхилення центру схвата маніпулятора точки М від її номінального розташування на безлічі можливих конфігурацій механізму. В результаті погрішностей точка М описує в просторі деякий еліпсоїд, який називається еліпсоїдом відхилень (рис. 20.10).


Рис. 20.10

Контрольні питання до лекції 20

1. Який план застосування методу матриць при аналізі кінематичного ланцюга маніпулятора?(стр.2-5)

2. У якій послідовності проводиться силовий розрахунок маніпуляторів? (стр.7-8)

3. Для чого проводиться урівноваження механізмів маніпуляторів?(стр.11-13

Література до лекції 20.

  1. Силовий розрахунок, урівноваження, проектування механізмів і механіка маніпуляторів: Навчальний посібник для студентів змішаної форми навчання / І.Н.Чернишева, А.К.Мусатов,н.А.Глухов і др.; Під ред. А.К.Мусатова. - М.: Вид-во МГТУ, 1990. - 80с., мул.
  2. Механіка промислових роботів: Навчань. допомога для втузів: У 3-х кн. / під ред. К.В.Фролова, Е.І.Воробйова. - М.: Висш.шк., 1988.
  3. Р.Пол "Моделювання, планування траєкторій і управління рухом робота - маніпулятора" - М.: Наука, 1976.

Завдання механіки маніпуляторів. Кінематичний аналіз механізму маніпулятора. Динаміка маніпуляторів промислових роботів