Возникновение колебаний давления

Оглавление

Введение

I. Общие сведения

I. 1. Инерционное поперечные колебания обтекаемые подводных трубопровод

I. 2. Возникновение колебаний давления

II. Теоретическая часть инерционных колебаний на подводных трубопроводах

II. 1. Сила сопротивления при колебаниях подводных трубопроводов

II. 2. Колебание трубопроводов

Заключение

Список литературы

Введение

Трубопроводный транспорт является одним из самых экономичных и надежных способов для доставки жидких и газообразных энергоносителей на значительные расстояния. Технические и эксплуатационные характеристики этих трубопроводов обеспечиваются за счет выбора труб с необходимыми физико-механическими свойствами металла, изоляционного покрытия и конструктивных решений. В процессе длительной эксплуатации внешние условия среды и технические характеристики трубопровода изменяются, в результате чего, заложенные при проектировании запасы прочности, надежности и безопасности могут быть исчерпаны, а трубопровод перейти в состояние, при котором возможно его разрушение.

В настоящее время значительная часть потенциально опасных промышленных объектов России, в том числе и трубопроводов (сухопутных и подводных), выработала гарантийные сроки эксплуатации, предусмотренные проектными решениями. Это относится не только к сухопутным трубопроводам, но и к подводным (морским, речным). Причем именно подводные трубопроводы работают в наиболее сложных и труднодоступных условиях. По некоторым экспертным оценкам, идет рост аварийных отказов на магистральных трубопроводах, и в отдельные годы достигает 80-100 случаев. Высокая аварийность данных трубопроводов, по мнению специалистов, была заложена уже на стадии проектирования, так как одним из основных требований было снижение стоимости проекта без необходимого обоснования надежности и безопасности сооружений.

I. Общие сведения

На обтекаемый морским или речным течением подводный трубопровод действует горизонтальная сила вязкого сопротивления, пропорциональная квадрату скорости потока воды. При этом если окружающая среда стратифицирована, то обтекаемый потоком трубопровод будет генерировать внутренние волны, вследствие чего возникнет дополнительное волновое сопротивление. Условия, благоприятствующие возникновению внутренних волн при обтекании подводного трубопровода, могут создавать придонные мутьевые потоки, возникающие при подъеме со дна твердых микро и мелкозернистых частиц грунта. Эффективная плотность таких потоков может превышать плотность чистой воды на 10 % и более, а толщина достигать нескольких десятков метров. Придонные потоки разделяют, в частности, на так называемые грязевые потоки и взвесенесущие турбулентные течения. Первые — концентрированные донные пограничные слои плотностью более 0,01 г/см3 . На такие потоки большое влияние оказывают приливы и волны. Вторые — взвесенесущие турбулентные потоки плотностью менее 0,01 г/см3. Однако непосредственно у дна последние имеют более высокую концентрацию взвешенных частиц. Используемые в настоящем анализе подходы к расчету силовых воздействий на подводный трубопровод, связанных с образованием внутренних волн в стратифицированном потоке, основаны на результатах работ авторов. Эти работы были выполнены в целях изучения возмущений морской поверхности, возникающих при обтекании глубинных препятствий стратифицированным морским течением. Важнейшими величинами, подлежавшими определению в этих работах, являлись комплексный потенциал и комплексная скорость возмущенного препятствием потока. В настоящем анализа проведения графика через эти величины определяются дополнительные силовые воздействия на трубопровод.

I. 1. Инерционное поперечные колебания обтекаемые подводных трубопровод

При обтекании трубопровода потоком жидкости возникают не только гидродинамические силы, обусловливающие его колебания, окружающая трубопровод вода оказывает также инерционное и демпфирующее воздействие.

Инерционное влияние воды заключается в следующем. Окружающая колеблющийся трубопровод вода вовлекается в колебательное движение и оказывает дополнительное воздействие на колеблющуюся систему, т. е. к силам инерции колеблющегося трубопровода добавляется инерционное воздействие так называемой присоединенной массы жидкости. Обычно под присоединенной массой жидкости понимается отношение составляющей гидродинамического давления, действующей в одной фазе с силами инерции конструкции, к ускорению соответствующей точки этой конструкции.

В настоящее время вопросам определения присоединенной массы жидкости применительно к различным элементам гидротехнических сооружений посвящено большое число теоретических и экспериментальных исследований. Теоретические исследования поперечных колебаний стержней в жидкости развиваются по двум направлениям. В первом направлении при решении данной задачи граничные условия для потенциала скорости принимаются на изогнутой поверхности стержня. Присоединенная масса жидкости в этом случае может быть определена по формулам гидродинамики.

Во втором направлении при исследовании гидроупругости решаются две независимые задачи— задача гидродинамики и задача теории колебании. При таком подходе сначала определяется форма колебаний конструкции в пустоте, затем инерционное и демпфирующее влияния жидкости, при этом форма колебаний принимается такой же, как и в пустоте. В этом случае задача о колебаниях конструкции в жидкости уже не является в строгом смысле задачей гидроупругости, поскольку теряется зависимость гидродинамического давления на конструкцию от деформации последней. Сопоставление результатов расчетов, выполненных по методам обоих направлений, с данными экспериментов показывает хорошее совпадение.

Решение задач по методам первого направления весьма затруднительно, поэтому в настоящее время для практических расчетов в основном используют методы второго направления (упрощенная задача гидроупругости), применяя которые можно получить решение для инерционного и демпфирующего воздействии водной среды на колебания некоторых элементов сооружений.

При решении задачи упругих колебаний стержней в безграничной жидкости получаются сложные выражения для определения присоединенной массы или частоты собственных колебаний стержней в жидкости. Поэтому некоторые исследователи считают, что для упругоколеблющегося стержня присоединенную массу жидкости можно принимать как и для абсолютной жесткой балки, т. е. величина присоединенной массы не зависит от формы колебаний.

I. 2. Возникновение колебаний давления

При гибке труб происходит утонение их стенок, искажение поперечного профиля в местах максимальной кривизны, образуются гофры и другие дефекты, которые при известных колебаниях давления рабочей жидкости (пульсации, гидроударах) в системе приводят к разрушению трубопроводов.

Необходимо отметить, что радиусы изгиба менее 3,51> не рекомендуется применять на некоторых участках гидросистемы (от насоса до кранов потребителей), а также на участках гидравлической системы, где возможны пульсации давления рабочей жидкости и интенсивные колебания рабочего давления.

Количество припоя подбирают по образцу и в дальнейшей работе его колебание не должно превышать 15%.

Ко вторым относятся усилия, возникающие в результате колебаний давления жидкости, пульсаций и гидравлических ударов в трубопроводах, а также вследствие их колебаний и вибраций.

Обычно различают периодические и непериодические колебания давления.

Однако практика показала, что в действительности процесс разгрузки насосов не проходит так гладко, а сопровождается возникновением высокочастотных колебаний давления.

При такой пульсации давления трубопроводы испытывали, кроме повышенных нагрузок от давления, еще переменные нагрузки, связанные с возникновением поперечных колебаний.

К непериодическим колебаниям давления прежде всего следует отнести гидравлические удары.

При некоторых условиях возможно возникновение внутреннего резонанса в системе, который может существенно изменить движение жидкости в трубопроводах, а также привести к возбуждению резонансных колебаний отдельных участков трубопроводов.

Первую резонансную частоту колебаний жидкости в трубопроводе можно определить с учетом того, что время одного цикла изменения давления

Это объясняется наличием рассеяния энергии колебаний в жидкости.

В данном случае получена его суммарная величина, учитывающая внутреннее трение в жидкости, трение жидкости о стенку трубопровода, внутреннее трение в материале стенок трубопровода, совершающего колебания вместе с заключенной в нем жидкостью, затухание колебаний вследствие рассеяния энергии на сжатие пузырьков воздуха, находящегося в жидкости.

II. Теоретическая часть инерционных колебаний на подводных трубопроводах

Колеблющийся подводный трубопровод имеет длину, значительно превышающую его диаметр (при меньшей длине колебания трубопроводов не происходят), максимальная амплитуда колебании также значительно меньше его длины. Поэтому можно считать, что при колебаниях угол между осью трубы и нормалью к ней практически мало отличается от 90°. Очевидно, в этом случае величины присоединенной массы для жесткого цилиндра и упругоколеблющегося трубопровода такого же диаметра должны различаться незначительно, т. е. результаты экспериментов. полученные п условиях плоской задачи, можно использовать применительно к трубопроводам, представляющим собой пространственную конструкцию. Это предположение подтверждается результатами экспериментов, выполненных авторами с жесткими и упругими моделями цилиндров.

Следует отметить, что при определении собственных частот высших тонов изгибных колебаний стержней и соответствующих им значений присоединенной массы жидкости необходимо учитывать деформацию сдвига и инерцию поворота сечения. При неучете этих факторов величина присоединенной массы жидкости будет зависеть от номера гармоники колебаний, что и имело место во многих ранее выполненных исследованиях.

Таким образом, присоединенная масса жидкости для колеблющегося трубопровода в безграничной жидкости принимается как и для жесткого тела по формуле

(1)

где р —плотность жидкости; D и l — внешний диаметр и длина трубопровода.

При колебаниях подводных трубопроводов могут быть самые разнообразные граничные условия (расположение трубопровода на дне, вблизи дна и свободной поверхности, в траншее), затрудняющие теоретическое определение присоединенной массы жидкости. Поэтому для установления инерционного влияния окружающей воды на колебания подводного трубопровода авторами были выполнены экспериментальные исследования применительно к различным условиям практики.

Существуют различные экспериментальные методы определения присоединенной массы. В приводимых исследованиях присоединенную массу определяли сравнением частот вертикальных колебаний цилиндра в воздухе и в жидкости. Основное достоинство этого метода — простота установки и получение достоверных данных, так как опыты проводятся в реальной жидкости с учетом реальных граничных условий.

Опыты проводили в гидравлическом лотке прямоугольного сечения размером 1X1, 5x12 м в условиях плоской и пространственной задач. Для случая плоской задачи применяли жесткие цилиндры диаметрами D=28,5108 мм, длиной L около 1000 мм. Для случая пространственной задачи использовали модели цилиндров размерами D = 32/1 мм, L=4481 мм; D=33/2 мм, L — 2894 мм; D=51/1,4 мм и L=5400 мм. Цилиндры по концам закреплялись шарнирно и представляли собой систему с распределенными параметрами, собственные колебания их соответствовали первому тону. Частоту и амплитуду колебаний измеряли тензорезисторами с использованием усилителя ТА-5 и осциллографа Н700.

Опыты проводились для следующих безразмерных параметров: относительное расстояние от свободной поверхности до верха образующей цилиндра h/D=0; 0,25; 0,5; 1,0; 1,5; 2.0; 3,0 и 4.0; относительное расстояние от дна лотка до нижней образующей цилиндра s/D=0.25; 0.5; 0,75; 1.0; 1,5; 2.0; 2,5; 3.0 и 4.0.

При колебаниях трубопроводов в траншеях исследовалось влияние на присоединенную массу следующих параметров: относительное удаление трубопровода от дна s/D = 0,25; 0.5; 1,0; 1,5; 2,0; угол заложения откосов траншеи а = 0; 45; 60 и 90°; относительная ширина траншеи но дну b/D = 2; 3; 4 и 5.

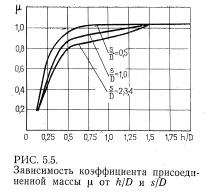
Результаты экспериментов представлены на графике (рис. 1) зависимости коэффициента присоединенной массы р (отношение присоединенной массы mпр к массе жидкости, заключенной в объеме цилиндра mv, т. е. = mпр/mv) от положения, занимаемого цилиндром относительно дна s/D и свободной поверхности h/D. Как видно из графика, коэффициент присоединенной массы повышается с уменьшением s/D и снижается с уменьшением h/D. При удалении цилиндра на расстояние около 3D и более от дна и свободной поверхности коэффициент присоединенной массы практически остается постоянным и не зависит от s/D и h/D. Снижение с уменьшением h/D<3D объясняется снижением инерционного воздействия окружающей трубопровод поды и появлением волновой составляющей гидродинамического давления, которая сдвинута относительно перемещения трубопровода по фазе на /2 и играет роль «присоединенного трения».

При частичном погружении цилиндра в воду (например, в случае укладки трубопровода свободным погружением или расположении трубопровода на плаву) расчетная схема его соответствует балке на нелинейном упругом основании, и частоты колебаний трубопровода значительно уменьшаются вследствие влияния упругости основания.

Для расчетов колебаний подводных трубопроводов применительно к различным условиям практики величину присоединенной массы следует определять по формуле

mпр = mv (2)

Значение коэффициента присоединенной массы принимается в зависимости от расположения трубопровода относительно дна и свободной поверхности потока или траншеи но графикам рис. 1.

II. 1. Сила сопротивления при колебаниях подводных трубопроводов

Для оценки напряженного состояния колеблющегося подводного трубопровода необходимо установить величину и основные зависимости сил сопротивления (демпфирование, рассеяние энергии) при колебаниях. Рассеяние энергии при колебаниях подводных трубопроводов складывается из потерь на гидродинамические сопротивления, сопротивление в материале конструкции трубопровода (труба, изоляция, футеровка, бетонное покрытие, балластировка) и потерь в грунт через опоры. Гидродинамическое сопротивление, потери энергии в грунт через опоры, потерн за счет трения футеровки и балласта о поверхность трубы будем относить, как это принято в теории колебаний, к внешним источникам рассеяния энергии в отличие от внутренних источников, к которым относится рассеяние энергии в материале трубы.

Внутреннее рассеяние является функцией напряжения и скорости деформации в материале трубопровода. Существуют различные гипотезы внутреннего трения при колебаниях упругих систем, некоторые из них хорошо совпадают с результатами экспериментов, но с математической точки зрения сложны и значительно затрудняют динамический расчет.

Гидродинамическое сопротивление при колебаниях включает рассеяние энергии па вихреобразование, сопротивление трения и волновое сопротивление.

Рассеяние энергии в грунт через опоры и вследствие трения футеровки и пригрузки по аналогии с классификацией, принятой в теории колебаний механических систем, можно отнести к конструкционным потерям. Величина и расчетные зависимости конструкционных потерь для подводных трубопроводов пока еще не изучены.

Учитывая сложность аналитической оценки сил сопротивления со всеми их составляющими, авторами проведены специальные исследования в натурных условиях по определению основных факторов, влияющих на сопротивление при колебаниях трубопроводов.

На основании результатов исследований колебаний надземных и подводных магистральных трубопроводов можно сделать вывод, что при значительной длине подводного участка трубопровода потерн энергии в материале трубы, изоляции и футеровки, а также рассеяние энергии через опоры в грунт малы по сравнению с гидродинамическими потерями. Следовательно, в некоторых случаях при колебаниях подводных трубопроводов основными можно считать гидродинамические силы сопротивления.

Значительная трудность теоретического определения сил сопротивления при колебаниях подводных трубопроводов обусловливает необходимость их экспериментального исследования. Одним из проявлений рассеяния энергии является затухание колебаний, приводящее к изменению амплитуд. Закон погашения амплитуд свободных колебании характеризует функцию сил сопротивления и может быть определен по развертке собственных затухающих колебаний.

Для определения сил сопротивления применительно к колебаниям подводных трубопроводов были выполнены эксперименты в условиях плоской и пространственной задач. Для случая плоской задачи использовали жесткие модели цилиндров диаметром D=32; 51; 100 мм и длиной L=1000 мм. Эти модели закреплялись на упругих подвесах и представляли собой колебательную систему с одной степенью свободы. Для случая пространственной задачи применяли модели цилиндров: D=32/1 мм, L=4481 мм; D=33/2 мм, L=2894 мм; D=51/1,4 мм; L=3752 мм, которые закреплялись шарнирно по концам и представляли собой колебательную систему с распределенными параметрами. Колебания цилиндров соответствовали первому тону. Силы сопротивления определяли по затуханию собственных колебаний. С помощью специального устройства цилиндры выводили из положения равновесия и они совершали собственные затухающие колебания. Частота и амплитуда колебаний измерялись тензорезисторами, наклеенными на упругие подвесы, и через усилитель ТА5 регистрировались осциллографом Н700.

В опытах наряду с силами гидродинамического сопротивления учитывались и силы сопротивления в элементах закреплений и упругих подвесах моделей. Декремент колебаний, характеризующий гидродинамические силы сопротивления г, определяли по формуле

г = - 1 (3)

где —декремент колебаний с учетом всех сил сопротивления (гидродинамические, конструкционные, в материале цилиндра); 1—декремент колебаний, соответствующий конструкционным силам сопротивления и рассеянию энергии в материале цилиндра.

Значения определяли по колебаниям цилиндров в воде, 1 — по колебаниям тех же цилиндров в воздухе.

В формуле (5.10) и 1, соответствовали одинаковой амплитуде колебаний. В экспериментах имело место интенсивное затухание свободных колебаний цилиндров, поэтому декременты колебаний определяли по формуле

(4)

где dai/dn — интенсивность убывания амплитуды колебаний вдоль оси циклов п затухающих колебаний.

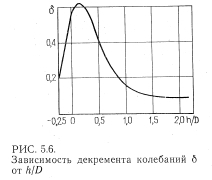
Рис. 2 Зависимость декремента колебаний

Результаты опытов показывают, что при отсутствии влияния дна и свободной поверхности декремент колебании г несущественно зависит от амплитуды колебаний, и поэтому в практических расчетах гидродинамические силы сопротивления при колебаниях можно считать линейно зависящими от скорости перемещения. Декремент колебаний г значительно зависит от расположения трубопровода относительно свободной поверхности при h/D<1,5 (рис. 2).

При изменении h/D от 1,5 до 0,15 г возрастает от 0,1 до 0.620,82. Такое повышение г объясняется увеличением волновой составляющей гидродинамического давления, которая сдвинута относительно перемещения трубопровода по фазе на /2 и действует в одной фазе с силами гидродинамического сопротивления. Как показывают результаты экспериментов, с уменьшением h/D<1,5 возрастает влияние составляющих гидродинамического давления, эквивалентных силам сопротивления (увеличивается «присоединенное трение»), и уменьшается влияние составляющих гидродинамического давления, эквивалентных инерционному воздействию (уменьшается коэффициент присоединенной массы ). С уменьшением относительного расстояния трубопровода от дна s/D до 0,5 отмечено незначительное уменьшение декремента колебании г.

При расположении трубопровода в подводной траншее величина г зависит от крутизны откоса траншеи и относительной ширины траншеи по дну bT/D.

Рассмотренные выше значения и зависимости для декрементов колебаний можно использовать в динамических расчетах подводных трубопроводов в случае, если гидродинамические силы сопротивления значительно превышают конструкционные. Величина декремента колебания , характеризующая суммарные силы сопротивления, может быть установлена па основании экспериментальных исследований в натурных условиях. Возможно, величина есть функция амплитуды колебаний.

От назначения величины суммарных сил сопротивления существенно зависят амплитуда колебания и динамические напряжения в трубопроводе. Кроме того, величина суммарных сил сопротивления позволяет установить возможность возникновения колебаний или диапазон изменения приведенной скорости, при котором будут происходить колебания трубопровода.

Для ориентировочной опенки возникновения колебаний подводных трубопроводов можно использовать величину безразмерного параметра демпфирования

(5)

где т — масса единицы длины трубопровода с учетом присоединенной массы жидкости тпр, массы изоляции, балластировки и продукта, заполняющего трубу; р — плотность окружающей трубопровод воды.

Критическое значение кр >, выше которого не наблюдается колебаний в направлении потока, равно 1,2. Для колебаний в поперечном к потоку направлении кр>=17.

С увеличением уменьшается диапазон приведенной скорости v =v/nD= 1/Sh, при котором происходят колебания подводного трубопровода. При значениях приведенной скорости v>1 иногда происходят колебания с частотой срыва вихрей, отличающейся от частоты собственных колебаний трубопровода, а v<1,2 колебания цилиндрических конструкций не наблюдаются.

II. 2. Колебание трубопроводов

Колебания давления рабочей жидкости в трубопроводах опасны не только тем, что создают высокие пики давления, но и тем, что при определенных условиях могут вызывать весьма опасные вибрации самих трубопроводов.

Поперечные колебания трубопроводов

В практике известно много случаев разрушения трубопроводов гидравлических систем, обусловленных поперечными колебаниями, которые могут возникать в результате передачи импульсов от элементов конструкции машины или агрегатов, а также от потока движущейся в трубопроводе рабочей жидкости.

При резонансных колебаниях значительно увеличивается амплитуда колебаний, а следовательно, и уровень действующих в трубопроводе напряжений.

Резонансные колебания трубопроводов возникают в том случае, когда частота вынужденных колебаний совпадает с частотой собственных колебаний какого-либо участка трубопровода или кратна ей.

Источники периодически действующих сил, особенно пульсации, создаваемые насосами, способны вызвать вынужденные колебания трубопроводов.

По мере приближения частоты вынужденных колебаний к частоте собственных колебании наступают биения.

Поперечные колебания и динамическая прочность напорных трубопроводов в связи с кавитационными явлениями в турбинах.

О поперечных колебаниях трубопроводов.

О параметрических колебаниях трубопроводов.

Колебания и динамическая устойчивость трубопроводов.

Колебания трубопроводов.

Влияние типа крепления на частоту собственных колебаний трубопроводов.

Проведенные испытания на керосине показали надежность таких соединений при резких колебаниях температуры до 340° С и давлении 80 кГ/см2.

Испытания этого типа соединений, проведенные за рубежом на трубах из нержавеющей стали с наружным диаметром 12,7 мм и толщиной стенки 0,9 мм, показали, что при температуре 20° и рабочем давлении 350 кГ/см2 образцы выдержали 10-10е циклов изгибных колебаний.

Например, неправильный выбор расстояния между колодками крепления может привести к возникновению опасных резонансных колебаний отдельных участков трубопровода и, как следствие, к его усталостным разрушениям.

Заключение

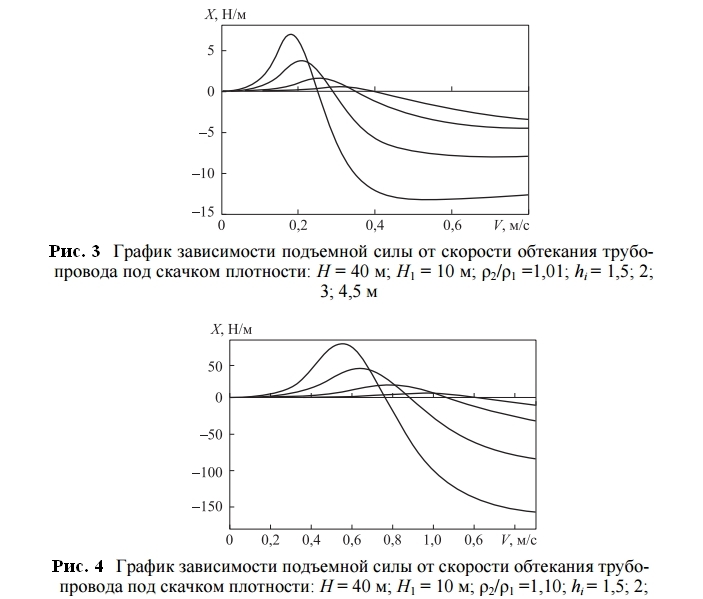
При возрастании внутреннего давления частота собственных колебаний криволинейного трубопровода возрастает, так как гидравлические агрегаты, к которым крепят трубопровод, в этом случае в меньшей степени препятствуют возникающей осевой деформации трубопроводов. А также при значительном возрастании плотности взвесенесущего потока волновое сопротивление трубопровода также существенно возрастает до значений, которыми нельзя пренебречь при анализе безопасности функционирования трубопровода. Отметим важную особенность подъемной силы, действующей на трубопровод. Как видно из проведенных расчетов, в относительно узком диапазоне изменения скорости потока подъемная сила резко меняет свое направление на противоположное (см. рис. 3, 4). При наличии существующих в реальных условиях моря неоднородностей в структуре горизонтального потока этот эффект может привести к возникновению противоположно направленных по вертикали силовых воздействий, рассредоточенных по длине трубопровода, что необходимо учитывать при проектировании и прокладке по морскому дну трубопроводных систем и других подводных конструкций.

Список литературы

1. П. П. Бородавкин, В. Л. Березин, О. Б. Шадрин. М.: Недра, 1979 г.
2. Владимиров И.Ю., Корчагин Н.Н., Савин А.С. Моделирование волнового воздействия стратифицированного течения на подводный трубопровод.
3. Корчагин Н.Н., Савин А.С., Савина Е.О. Волны на поверхности моря, обусловленные обтеканием подводного препятствия. Океанология, 2009г.
4. Владимиров И.Ю., Корчагин Н.Н., Савин А.С. Волновое воздействие взвесенесущего потока на обтекаемое препятствие. Докл. РАН, 2015г.

1. http://mmcm.bmstu.ru/articles/56/

Возникновение колебаний давления