Виды понятий. Логическая характеристика понятий

АНО ВПО «НАЦИОНАЛЬНЫЙ ИНСТИТУТ ИМЕНИ ЕКАТЕРИНЫ ВЕЛИКОЙ»

ФАКУЛЬТЕТ УПРАВЛЕНИЯ, ЭКОНОМИКИ И ФИНАНСОВ

Кафедра менеджмента

Контрольное задание

по дисциплине: «ЛОГИКА»

СОДЕРЖАНИЕ:

1. Виды понятий. Логическая характеристика понятий.
2. Отношения между понятиями.
3. Операции над понятиями.
4. Виды простых суждений. Структура, состав.
5. Логический квадрат. Определение истинности по логическому квадрату.
6. Выделяющие и исключающие суждения.
7. Сложные суждения.
8. Отрицание суждений.
9. Модальность суждений.
10. Непосредственные умозаключения.
11. Простой категорический силлогизм.
12. Умозаключения из суждений с отношениями.
13. Выводы из сложных суждений. Виды дедуктивных умозаключений: условный силлогизм, разделительный силлогизм, условно-разделительный силлогизм.
14. Сложные и сокращенные силлогизмы.
15. Виды индуктивных умозаключений.
16. Методы установления причинных связей.
17. Умозаключение по аналогии.
18. Основные формально-логические законы.
19. Доказательство и опровержение.

1. Виды понятий. Логическая характеристика понятий.

В зависимости от специфики объема и содержания все понятия делятся на определенные виды. По объему: единичные и общие понятия; собирательные и несобирательные. По содержанию: конкретные и абстрактные понятия; положительные и отрицательные; безотносительные и соотносительные. [Демидов И.В. стр. 62]

Единичные и общие понятия. Понятие, в котором мыслится один элемент, называется единичным; понятие, в котором мыслится множество элементов, называется общим. Например, «Российская Федерация» – единичное понятие, «федерация» – общее.

Собирательные и несобирательные понятия. Понятия, в которых мыслятся признаки некоторой совокупности элементов, составляющих единое целое, называются собирательными (например, «коллектив», «полк»). Эти понятия отражают множество элементов, однако это множество мыслится как единое целое. Содержание собирательного понятия нельзя отнести к каждому отдельному элементу, входящему в его объем, оно относится ко всей совокупности элементов. Понятие, в котором мыслятся признаки, относящиеся к каждому его элементу, называется несобирательным. Таковы, например, понятия «звезда», «командир полка».

В процессе рассуждения общие понятия могут употребляться в разделительном и собирательном смысле. Если высказывание относится к каждому элементу класса, то такое употребление понятия будет разделительным; если же высказывание относится ко всем элементам, взятым в единстве, и неприложимо к каждому элементу в отдельности, то такое употребление понятия называется собирательным.

Конкретные и абстрактные понятия. Понятие, в котором мыслится предмет или множество предметов как нечто самостоятельно существующее, называется конкретным; понятие, в котором мыслится признак предмета или отношение между предметами, называется абстрактным. Так, понятия «книга», «город» являются конкретными. Понятия «книжный» (переплет), «городской» (житель) – абстрактными. Различие между конкретными и абстрактными понятиями основано на различии между предметом, который мыслится как целое, и свойством предмета, отвлеченным от последнего и отдельно от него не существующим.

Положительные и отрицательные понятия. Понятия, содержание которых составляют свойства, присущие предмету, называются положительными. Понятия, в содержании которых указывается на отсутствие у предмета определенных свойств, называются отрицательными. Так, понятия «грамотный», «порядок» являются положительными; понятия «неграмотный», «беспорядок» – отрицательными.

Безотносительные и соотносительные понятия. Понятия, отражающие предметы, существующие раздельно и мыслящиеся вне их отношения к другим предметам, называются безотносительными. Таковы понятия «адвокат», «государство» и др. Соотносительные понятия содержат признаки, указывающие на отношение одного понятия к другому понятию. Например, «родители» (по отношению к понятию «дети»), «начальник» (по отношению к понятию «подчиненный»). Соотносительными являются также понятия «брат», «сосед» и др. В этих понятиях отражены предметы, существование одного из которых не мыслится вне его отношения к другому.1

Определить, к какому из указанных видов относится конкретное понятие, означает дать ему логическую характеристику. Так, давая логическую характеристику понятию «Российская Федерация», укажем, что это понятие единичное, собирательное, конкретное, положительное, безотносительное. Если понятие имеет несколько значений, то логическая характеристика ему дается в соответствии с каждым значением. Таким образом, логическая характеристика понятий помогает уточнить их содержание и объем, что дает возможность более точного употребления данных понятий в процессе рассуждения.

1. Отношения между понятиями.

Все предметы находятся во взаимодействии и взаимообусловленности, поэтому и понятия, отражающие данные предметы, также находятся в определенных отношениях. Конкретные виды отношений устанавливаются в зависимости от содержания и объема понятий, которые сравниваются.2

По содержанию между понятиями могут быть только два вида отношений – сравнимость и несравнимость. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми (безответственность и нитка, романс и кирпич). Между ними невозможны логические отношения.

Сравнимые понятия – это понятия, имеющие в своем содержании общие, существенные признаки (по которым они и сравниваются). Например, право и мораль, юрист и адвокат. Отношения между понятиями изображают с помощью схем – кругов Эйлера.

Между сравнимыми понятиями возможны два вида отношений по объему: совместимость и несовместимость, а сами соотносящиеся понятия называются совместимыми или несовместимыми.

Совместимые понятия – это такие, объемы которых полностью или частично совпадают. Между совместимыми понятиями складываются следующие отношения:

1. Равнообъемность. Равнообъемными или равнозначными называются понятия, которые различаются по своему содержанию, но их объемы совпадают. Например, «Л.Н. Толстой» – А и «автор романа «Война и мир» – В. Объемы тождественных понятий изображаются кругами, полностью совпадающими.

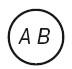
1. Перекрещивание. Перекрещивающимися называются понятия, объемы которых частично совпадают. Например «студент» и «спортсмен», «юрист» и «писатель». Они изображаются пересекающимися кругами. В перекрещивающейся части двух кругов мыслятся студенты, являющиеся спортсменами. В левой части круга мыслятся студенты, не являющиеся спортсменами, а в правой части – спортсмены, не являющиеся студентами.

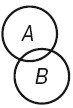
1. Подчинение. В отношении подчинения (субординации) находятся понятия, если объем одного полностью входит в объем другого, но не исчерпывает его. Это отношение вида – В и рода – А (млекопитающее и кошка).

Несовместимыми называются понятия, объемы которых не совпадают. Несовместимые понятия могут находиться между собой в следующих отношениях:

1. Соподчинение. В отношении соподчинения (координации) находятся понятия, объемы которых исключают друг друга, но принадлежат некоторому более общему родовому понятию. Например, «ель» – B, «береза» – C принадлежат объему понятия «дерево» – А. Они изображаются отдельными неперекрещивающимися кругами внутри одного общего круга. Это виды одного и того же рода.

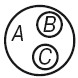
1. Противоположность. В отношении противоположности (контрарности) находятся два понятия, признаки которых противоречат друг другу, а сумма их объемов не исчерпывает родового понятия (храбрость – трусость).

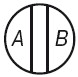
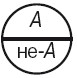
1. Противоречие. В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя никакими другими. Если одно понятие обозначить A (например, белая краска), то другое понятие, находящееся с ним в отношениях противоречия, следует обозначить не-А (т.е. не белая краска). Круг Эйлера в этом случае делится пополам, и между ними нет третьего понятия.3

1. Операции над понятиями.

Основные логические операции с понятиями: обобщение и ограничение понятий, их определение и деление. В основе данных операций лежат родовидовые отношения между понятиями. Логические операции обобщения и ограничения основаны на законе обратного отношения между объемом и содержанием понятия. Данные операции имеют противоположную направленность.

Ограничение – это логическая операция перехода от родовых понятий к видовым понятиям путем прибавления к содержанию родового понятия видообразующего признака. Так, если к содержанию понятия «экономист» добавить видообразующий признак, показывающий его специализацию, то получим новое понятие, например, «экономист-финансист», которое является видовым понятием по отношению к исходному, родовому понятию «экономист». Логическая операция ограничения понятия широко применяется в экономической сфере. При ограничении понятий важно соблюдать правило последовательного перехода от рода к виду. Пределом ограничения является единичное понятие.

Обобщение – это логическая операция перехода от видового понятия к родовому понятию путем исключения из содержания данного видового понятия его видообразующего признака. Так, если из содержания понятия «экономическая академия» исключить видовой признак «экономическая», то получим родовое понятие «академия». Для соблюдения правильности обобщения необходимо последовательно переходить от вида к роду, включающему в себя данный вид. Пределом обобщения являются категории – наиболее общие фундаментальные понятия, отражающие существенные, закономерные связи объективной действительности и познания. Это обусловлено тем, что, чем больше объем понятия, тем оно глубже отражает предмет или класс однородных предметов.

Таким образом, изменяя объем исходного понятия, мы изменяем и его содержание, осуществляя тем самым переход к новому понятию – с меньшим объемом и большим содержанием (ограничение) или с большим объемом и меньшим содержанием (обобщение). Логические операции ограничения и обобщения имеют большое значение в процессе мышления: переходя от понятий одного объема к понятиям другого объема, мы уточняем предмет нашей мысли, делаем наше мышление более определенным и последовательным.4

В научной и практической деятельности нередко возникает необходимость раскрыть содержание понятий, которые употребляются в рассуждениях. Логическая операция, раскрывающая содержание понятия, называется определением (дефиницией). Понятие, содержание которого требуется раскрыть, называется определяемым. Понятие, которое раскрывает содержание определяемого понятия, называется определяющим. Выражая в сжатом виде знания о предмете, понятие является существенным моментом в познании действительности. В любой науке всем основным понятиям даются определения, причем в правовых науках точные определения понятий имеет не только теоретическое, но практическое значение.

При изучении какого-либо понятия нередко встает задача раскрыть его объем, т.е. распределить предметы, которые мыслятся в понятии, на отдельные группы. Так, чтобы лучше понять, что такое сделка (действие гражданина или организации, направленное на установление, изменение или прекращение гражданских прав и обязанностей), следует разделить сделки на виды: многосторонние, двусторонние и односторонние.

Логическая операция, раскрывающая объем понятия, называется делением. В операции деления следует различать делимое понятие – его объем следует раскрыть, члены деления – соподчиненные виды, на которые делится понятие (они представляют собой результат деления), и основание деления – признак, по которому производится деление.

Сущность деления состоит в том, что предметы, входящие в объем делимого понятия, распределяются по группам. Делимое понятие рассматривается при этом как родовое, и его объем разделяется на соподчиненные виды. Так, в приведенном примере делимое понятие «сделка» является родом, а члены деления «многосторонняя сделка», «двустороння сделка», «односторонняя сделка» – его видами. Основанием деления является число сторон сделки. Операция деления позволяет правильно распределить предметы по группам, изучить их, а, следовательно, глубже познать весь класс в целом.5

1. Виды простых суждений. Структура, состав.

Простые суждения подразделяются на виды по следующим признакам:

1. По объему субъекта (по количеству). Единичные суждения включают утверждение или отрицание об одном предмете. Формула такого суждения: «Это S есть (не есть) P». В частных суждениях что-либо утверждается или отрицается о части предметов некоторого класса. Эта часть может быть неопределенной и определенной. В неопределенных суждениях логическая схема такова: «Некоторые есть P». Слово «некоторые» придает им неопределенность. Например: «Некоторые проблемы политологии носят философский характер». Определенное частное суждение содержит знание и о той, и о другой части субъекта суждения. Оно имеет следующую логическую схему: «Только некоторые S есть P». Например: «Только некоторые проблемы языкознания носят философский характер». В общих суждениях что-либо утверждается или отрицается в каждом предмете данного класса. Логическая схема таких суждений имеет вид: «Все S есть P» или «Ни одно S не есть P»;
2. По качеству связки суждения могут быть утвердительные или отрицательные. Утвердительные суждения выражают принадлежность предмету некоторого признака. Например: «Научная организация труда повышает эффективность деятельности инженера». Отрицательные суждения выражают отсутствие у предмета некоторого признака. Например: «Ни один дельфин не является рыбой»;
3. По содержанию предиката суждения в логике делятся на суждения свойства (атрибутивные), суждения отношения (релятивные) и суждения существования (экзистенциальные). Суждения свойства отражают принадлежность или не принадлежность предмету мысли того или иного свойства, состояния, например: «В наше время приобретение философских знаний составляет важнейший элемент духовной культуры человека». Суждения отношения выражают различные связи между предметами мысли по месту, времени, величине и т.п. Например, суждение «Эверест выше Монблана» определяется отношением (через сравнение) одной горы с другой. Суждения существования призваны решать вопрос о наличии предмета нашей мысли – любого явления природы, общества или духовной жизни. Например: «Одним из объектов исследования социологии является общественное мнение».6

Таковы основные виды простых суждений. Любое суждение имеет количественную и качественную определенность. Поэтому в логике применяется объединенная классификация суждений по количеству и качеству: общеутвердительные суждения, общеотрицательные, частноутвердительные и частноотрицательные.

Общеутвердительное суждение – общее по объему и утвердительное по качеству связки. Его логическая структура – «Все S есть P», а символом служит латинская буква «A». Примером является: «Все бухгалтеры – экономисты».

Общеотрицательное суждение – общее по объему субъекта и отрицательное по качеству связки. Его логическая структура: «Ни одно S не есть P». Символом служит буква «Е». Например: «Ни один подложный документ не является доказательством».

Частноутвердительное суждение – частное по объему субъекта и утвердительное по качеству связки. Его логическая структура: «Некоторые S есть P». Символом служит латинская буква «I». Примеры таких суждений: «Некоторые депутаты – экономисты», «Некоторые писатели – фронтовики».

Частноотрицательное суждение – частное по объему субъекта и отрицательное по качеству связки. Его логическая структура: «Некоторые S не есть P», а символом служит буква «O». Примеры частноотрицательных суждений: «Некоторые европейские страны не являются членами Международного валютного фонда», «Некоторые государственные служащие не являются экономистами».7

Распределение терминов в суждениях

Термин	Вид суждения
	А	Е	J	O
S	+	+	–	–
P	– (+)	+	– (+)	+

1. Логический квадрат. Определение истинности по логическому квадрату.

Отношения между простыми суждениями обычно иллюстрируют с помощью схемы, получившей название «логический квадрат».

Логический квадрат (квадрат противоположностей) – это диаграмма, служащая для мнемонического запоминания логических отношений между видами суждений по объединенной классификации.

Вершины квадрата обозначают вид суждения по объединенной классификации A, Е, O, I. Стороны и диагонали символизируют логические отношения между простыми суждениями (кроме эквивалентных суждений). Верхняя сторона есть отношение A и E – противоположность (контрарность); нижняя сторона – отношение между I и O – частичная совместимость (субконтрарность); две вертикальные стороны – отношения между A и I (левая), Е и O (правая) – подчинение; диагонали – отношения между A и O, Е и I – противоречие (контрадикторность).

Логический квадрат нагляден и удобен в использовании и широко применяется в современной науке.8

1. Выделяющие и исключающие суждения.

Особое место в классификации суждений занимают выделяющие и исключающие суждения.

Выделяющие суждения отражают тот факт, что признак, выраженный предикатом, принадлежит (или не принадлежит) только данному и никакому другому предмету.

Выделяющие суждения могут быть единичными, частными и общими.

«Только Зимин является свидетелем происшествия» (S и только S есть P – единичное выделяющее суждение). Оно выражает знание о том, что Зимин является единственным свидетелем происшествия. Субъект и предикат этого суждения имеют одинаковый объем.

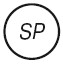
«Некоторые города – столицы государств» – пример частного выделяющего суждения (некоторые S и только S суть Р). Столицами государств могут быть только города, и притом только некоторая их часть. Предикат частного выделяющего суждения полностью входит в объем субъекта.

«Все преступления, и только преступления, предусмотренные законом, – общественно опасные деяния» – пример общего выделяющего суждения (все S, и только S суть Р). Объемы субъекта и предиката общего выделяющего суждения полностью совпадают.

Слова «только», «лишь», входящие в состав предложений, выражающих выделяющие суждения, могут находиться как перед субъектом, так и перед предикатом. Но они могут и вообще отсутствовать. В этих случаях установить, что данное суждение является выделяющим, помогает логический анализ.

Исключающим называется суждение, в котором отражается принадлежность (или непринадлежность) признака всем предметам, за исключением некоторой их части. Например, «Все студенты нашей группы, кроме Волкова, сдали экзамены». Исключающие суждения выражаются предложениями со словами «кроме», «за исключением», «помимо», «не считая» и т.п. (все S, за исключением S', суть Р).

Значение выделяющих и исключающих суждений состоит в том, что положения, выраженные в форме этих суждений, характеризуются точностью и определенностью, что исключает их неоднозначное понимание. Например, в Конституции РФ ст. 118 (ч. 1) и 123 (ч. 2) гласят: «Правосудие в РФ осуществляется только судом», «Заочное разбирательство уголовных дел в судах не допускается, кроме случаев, предусмотренных федеральными законами».9

1. Сложные суждения.

Все суждения можно разделить на две большие группы: простые и сложные.

Простым называется суждение, выражающее связь двух понятий. Например: «Некоторые вулканы действуют».

Суждение, состоящее из нескольких простых суждений, называется сложным. Например: «Прозрачный лес один чернеет, и ель сквозь иней зеленеет, и речка подо льдом блестит».

Сложные суждения делятся на соединительные и разделительные суждения.

Соединительные (конъюнктивные) суждения включают в качестве составных частей другие суждения-конъюнкты. Суждения-конъюнкты объединяются связками «и», «а», «но», «как», «так и», «также». Например, «Язык и мышление взаимодействуют в процессе перевода» или «Студент Иванов живет в Москве и учится в МГУ».

Разделительные (дизъюнктивные) суждения включают в качестве составных частей суждения-дизъюнкты, объединяемые связкой «или».

Различают слабую дизъюнкцию, когда союз «или» имеет соединительно-разделительное значение и не придает исключающего смысла входящим в сложное суждение составляющим. Например: «Люди обижают друг друга или из ненависти, или из зависти, или из презрения».

Сильная дизъюнкция, как правило, возникает, когда употребляется логический союз «либо», имеющий исключающий смысл. Например, в выражении М.Е. Салтыкова-Щедрина: «Либо в рыло, либо ручку пожалуйте» соединяются несовместимые друг с другом суждения.

Условные (импликативные) суждения – это такие суждения, которые образованы из двух посредством логических союзов: «если … то», «там … где», «постольку … поскольку». В качестве можно использовать мысль, высказанную поэтом Кабусом: «Если хочешь иметь друзей, то не будь мстительным». Аргумент, начинающийся словом «если», называется основанием. Составляющая часть, начинающаяся словом «то», – следствием.10

1. Отрицание суждений.

Отрицание суждения в логике – это замена существующей связки внутри сложного высказывания на другую связку, противоположную последней. Если мы говорим о формуле, в которой можно выразить отрицание сложных суждений, то нужно отметить, что отрицание графически выражается как горизонтальная черта над отрицаемым суждением. Таким образом, мы получим два понятия, объединенных логической связкой, над которыми проведена горизонтальная черта. Если такая черта уже есть, то для осуществления отрицания необходимо такую черту удалить.

Все сказанное выше относится к операциям, производимым с применением конъюнкции и дизъюнкции. Однако это не означает, что отрицание сложных суждений возможно, только если они содержат исключительно связки конъюнкцию и дизъюнкцию. Если необходимо осуществить операцию отрицания по отношению к суждению, содержащему импликацию, необходимо заменить это суждение так, чтобы при отсутствии каких-либо его изменений отбросить импликацию. Это означает, что необходимо подобрать суждение, эквивалентное данному суждению, которое при этом не содержало бы импликации. Когда мы говорим о суждении, эквивалентном суждению содержащему импликацию, но не содержащему ее, подразумевается замена этой связки на конъюнкцию или дизъюнкцию. Графически это выглядит как (a – b) = (a V b). Затем производится описанная выше операция, при которой знак конъюнкции меняется на дизъюнкцию, и наоборот.

Обычно в речи выражение отрицания сводится к добавлению приставки «не». Действительно, так как указанная приставка является отрицательной, ее применение для установления противоположности вполне оправдано.

Необходимо упомянуть о законах де Моргана. Они применяются в процессе отрицания сложных суждений и имеют формульное выражение. Таких законов и, соответственно, формул всего четыре:

1. a ^ b = a V b;
2. a ^ b = a V b;
3. a V b = a ^ b;
4. a V b = a ^ b.

Отрицание сложного суждения, где содержится конъюнкция или дизъюнкция, является простым вариантом, при котором достаточно лишь проведения операции отрицания. Формула, образованная при помощи законов де Моргана, выглядит следующим образом: (a ^ b) V (c ^ e) = (a V b) ^ (c V e).

Необходимо сказать, что суждения, отрицающие друг друга, не могут быть одновременно истинными или ложными. Ситуация противоречия или отрицания характеризуется тем, что одно из противоречащих понятий всегда истинно, а другое при этом ложно. Другого положения в этом случае быть не может.

Нельзя отождествлять операцию отрицания, в результате которой образуется новое суждение, от отрицания, являющегося частью отрицательных суждений. Отрицание суждений может производиться как в отношении всего суждения, так и его частей и выражается словами «не является», «не суть», «не есть», а также «неверно» и др. Таким образом, есть два вида отрицания – внутреннее и внешнее. Внешнее отрицает все суждение в целом. Например: «Некоторые солдаты не являются десантниками» – это внутреннее отрицание, в то время как суждение «Неверно, что Луна является планетой» – это отрицание внешнее. Таким образом, внешнее отрицание – это отрицание всего суждения в целом, тогда как внутреннее показывает факт противоречия или несоответствия предиката субъекту.

В виде формул можно отобразить следующие виды отрицательных суждений: «все S есть P» и «некоторые S не есть P» (общие суждения); «ни одно S не является P» и «некоторые S являются P» (частные суждения). Последний вид отрицательных суждений выглядит как «это S является P» и «это S не является P» (суждения, называемые единичными).11

1. Модальность суждений.

Рассматривая сущность и специфику простых и сложных видов суждений, важно иметь также представление об их модальности. 

Модальность суждения – это выраженная в суждении явно или неявно дополнительная информация. В логике различают три группы модальных суждений. 

Первая группа – истинная (алетическая) модальность. Это выраженная в терминах необходимости или возможности информация о логической зависимости между субъектом и предикатом суждения, либо о фактической зависимости между отражаемыми в них явлениями. В границах истинной или алетической модальности принято выделять, во-первых, логическую обусловленность, или детерминированность. Например, в суждении «Очевидно, что автор «Задонщины» был участником Куликовской битвы» устанавливается связь между освещаемыми событиями XIV века и непосредственными знаниями автора. Во-вторых, выделяют фактическую обусловленность. Так, в суждении «Париж расположен западнее Варшавы» устанавливается именно фактическая модальность.

Вторая группа – несомненная (эпистемическая) модальность. Она представляет собой выраженную в суждении информацию о характере принятия и степени обоснованности знания. Утверждение «Я знаю, что знаю мало в области философии» показывает обоснованность понимания данной проблемы. Знания в таких суждениях могут быть: достоверными, проблематичными, верифицированными, внелогическими. 

Третья группа – обязательная (деонтическая) модальность, которая является выражением в суждении побуждения людей к конкретному поведению в форме совета, команды, пожелания. Такой вид модальности суждений дает возможность логически анализировать следующие нормы: «имеет право», «может», «должен», «обязан» др.12 

1. Непосредственные умозаключения.

Суждение, содержащее новое знание, может быть получено посредством преобразования некоторого суждения. Так как исходное (преобразуемое) суждение рассматривается как посылка, а суждение, полученное в результате преобразования, – как заключение, умозаключения, построенные посредством преобразования суждений, называются непосредственными. К ним относятся:

1. Превращение – это преобразование суждения в суждение, противоположное по качеству с предикатом, противоречащим предикату исходного суждения. Превращение опирается на правило: двойное отрицание равносильно утверждению. Превращать можно общеутвердительные, общеотрицательные, частноутвердительные, частноотрицательные суждения. Суждение, полученное посредством превращения, сохраняет количество, но изменяет качество исходного суждения. Субъект исходного суждения не изменяется. Заключения, полученные посредством превращения, уточняют наши знания. Устанавливая отношения между субъектом и понятием, противоречащим предикату исходного суждения, мы рассматриваем предмет суждения с новой стороны, фиксируя внимание на свойстве, не совместимом со свойством, выраженным в предикате исходного суждения.
2. Обращение – это преобразование суждения, в результате которого субъект исходного суждения становится предикатом, а предикат – субъектом заключения. Обращение подчиняется правилу: термин, не распределенный в посылке, не может быть распределен в заключении. Различают простое (без изменения количества суждения) обращение и обращение с ограничением (если предикат исходного суждения не распределен, то он не будет распределен и в заключении, где он становится субъектом; его объем ограничивается).
3. Противопоставление предикату – это преобразование суждения, в результате которого субъектом становится понятие, противоречащее предикату, а предикатом – субъект исходного суждения. Противопоставление предикату может рассматриваться как результат превращения и обращения: превращая исходное суждение S – P, устанавливаем отношение S к не–Р; суждение, полученное путем превращения, обращается, в результате устанавливается отношение не–Р к S.
4. Умозаключения по логическому квадрату. Учитывая свойства отношений между категорическими суждениями A, Е, I, О, которые иллюстрированы схемой логического квадрата, можно строить выводы, устанавливая следование истинности или ложности одного суждения из истинности или ложности другого суждения. Данные выводы рассматриваются по: отношению противоречия (контрадикторности), противоположности (контрарности), частичной совместимости (субконтрарности), подчинения. 

1. Простой категорический силлогизм.

Простой категорический силлогизм состоит из трех категорических суждений, два из которых являются посылками, а третье – заключением. Например, «Обвиняемый имеет право на защиту. Гусев – обвиняемый. Гусев имеет право на защиту».

Расчленим суждения, из которых состоит силлогизм, на понятия. Этих понятий три, причем каждое из них входит в состав двух суждений: «Обвиняемый» – в 1-е (посылку) как субъект и во 2-е (посылку) как предикат; «имеет право на защиту» – в 1-е (посылку) и в 3-е (заключение) как их предикаты; «Гусев» – во 2-е (посылку) и в 3-е (заключение) как их субъекты.

Понятия, входящие в состав силлогизма, называют терминами силлогизма. Различают меньший, больший и средний термины.

Меньшим термином силлогизма называется понятие, которое в заключении является субъектом (в нашем примере понятие «Гусев»). Большим термином силлогизма называется понятие, которое в заключении является предикатом («имеет право на защиту»). Меньший и больший термины называются крайними и обозначаются соответственно латинскими буквами S (меньший термин) и P (больший термин).

Каждый из крайних терминов входит не только в заключение, но и в одну из посылок. Посылка, в которую входит меньший термин, называется меньшей посылкой, посылка, в которую входит больший термин, называется большей посылкой. В нашем примере большей посылкой будет первое суждение (1), меньшей – второе суждение (2).

Средним термином силлогизма называется понятие, входящее в обе посылки и отсутствующее в заключении (в нашем примере – «обвиняемый»). Средний термин обозначается латинской буквой М.

Обвиняемый (М) имеет право на защиту (Р).

Гусев (S) – обвиняемый (М).

Гусев (S) имеет право на защиту (Р).

Итак, простой категорический силлогизм – это умозаключение об отношении двух крайних терминов на основании их отношения к среднему термину.

Аксиома силлогизма обосновывает правомерность вывода, т.е. логического перехода от посылок к заключению: все, что утверждается или отрицается относительно всех предметов некоторого класса, утверждается или отрицается относительно каждого предмета и любой части предметов этого класса. В данном примере – все, что утверждается относительно всех обвиняемых, утверждается и относительно конкретного обвиняемого.13

1. Умозаключения из суждений с отношениями.

Умозаключение, посылки и заключение которого являются суждениями с отношениями, называется умозаключением с отношениями.

Например: Петр – брат Ивана. Иван – брат Сергея. Петр – брат Сергея.

Посылки и заключение в приведенном примере – суждения с отношениями, имеющие логическую структуру x R y, где х и у – понятия о предметах, R – отношения между ними.

Логическим основанием умозаключений из суждений с отношениями являются свойства отношений, важнейшие из которых симметричность, рефлексивность и транзитивность.

1. Отношение называется симметричным, если оно имеет место как между предметами х и y, так и между предметами y и х. Иначе говоря, перестановка членов отношения не ведет к изменению вида отношения. Симметричными являются отношения равенства (если a равно b, то и b равно a), сходства (если c сходно с d, то и d сходно с), одновременности (если событие х произошло одновременно с событием у, значит, и событие у произошло одновременно с событием х), различия и некоторые другие.
2. Отношение называется рефлексивным, если каждый член отношения находится в таком же отношении к самому себе. Таковы отношения равенства (если a = b, то a = a и b = b) и одновременности (если событие х произошло одновременно с событием у, значит, каждое из них произошло одновременно с самим собой).
3. Отношение называется транзитивным, если оно имеет место между x и z тогда, когда оно имеет место между x и y и между y и z. Иначе говоря, отношение является транзитивным (переходным) тогда и только тогда, когда из отношения между x и y и между y и z следует такое же отношение между x и z. Транзитивными являются отношения равенства (если a равно b и b равно c, то a равно c), одновременности (если событие х произошло одновременно с событием у и событие у одновременно с событием z, значит, событие х произошло одновременно с событием z), отношения «больше», «меньше» (а меньше b, b меньше с, значит, а меньше с), «позднее», «находиться севернее (южнее, восточнее, западнее)», «быть ниже, выше» и т.п.

Таким образом, истинность заключения из суждений с отношениями зависит от свойств отношений и регулируется правилами, вытекающими из этих свойств. В противном случае заключение может оказаться ложным. Так, из суждений «Сергеев знаком с Петровым» и «Петров знаком с Федоровым» не следует необходимого заключения «Сергеев знаком с Федоровым», так как «быть знакомым» не является транзитивным отношением.

1. Выводы из сложных суждений. Виды дедуктивных умозаключений: условный силлогизм, разделительный силлогизм, условно-разделительный силлогизм.

Умозаключения строятся не только из простых, но и из сложных суждений. Широко используются умозаключения, посылками которых являются условные и разделительные суждения. Особенность этих умозаключений в том, что выведение заключения из посылок определяется не отношениями между терминами, как в категорическом силлогизме, а характером логической связи между суждениями. Поэтому при анализе посылок их субъектно-предикатная структура не учитывается. Рассмотрим выводы из сложных суждений.

Условное умозаключение (условный силлогизм) – вид опосредованного дедуктивного умозаключения, в котором, по крайней мере, одна из посылок – условное суждение. Выделяют чисто условные и условно-категорические умозаключения.

Чисто условным умозаключением называется такое опосредованное умозаключение, в котором обе посылки и заключение являются условными суждениями. Его логическая структура такова: если а, то b; если b, то c; если а, то c. Вывод в чисто условном умозаключении основывается на правиле: следствие следствия есть следствие основания.

Условно-категорическим называется такое умозаключение, в котором одна из посылок – условное, а другая посылка и заключение – категорические суждения. Его логическая структура: Если а, то b. Данный вид умозаключения имеет два модуса – утверждающий и отрицающий. Каждый из них встречается в двух формах: правильной и неправильной. В правильных формах выводы имеют достоверный характер, а в неправильных – вероятностный характер.

Разделительным называется умозаключение, в котором одна или несколько посылок – разделительные суждения. Выделяют разделительно-категорические и условно-разделительные умозаключения. Разделительно-категорическим называется умозаключение, в котором одна из посылок – разделительное, а другая посылка и заключение – категорические суждения. Разделительно-категорическое умозаключение имеет два модуса: утверждающе-отрицающий и отрицающе-утверждающий.

Условно-разделительным, или лемматическим называется умозаключение, в котором одна посылка состоит из двух или боле условных суждений, а другая – разделительное суждение. По количеству следствий условной посылки (альтернатив) различают дилеммы, трилеммы, полилеммы. Дилемма – это условно-разделительное умозаключение с двумя альтернативами. В практике рассуждений встречаются два вида дилемм – конструктивная дилемма и деструктивная. В условной посылке конструктивной дилеммы устанавливается возможность двух условий и вытекающих из них двух следствий. Разделительная посылка ограничивает выбор только между этими двумя условиями, а в заключении утверждается возможность только одного следствия. В условной посылке деструктивной дилеммы устанавливается, что из двух оснований могут вытекать два следствия. В разделительной посылке отрицается одно из возможных следствий, а в заключении отрицается одно из возможных оснований.

В целом при правомерности выводов лемматических умозаключений нужно руководствоваться следующим: вывод правомерен, если ход рассуждений направлен от утверждения оснований к утверждению следствий или от отрицания следствий к отрицанию оснований.

Таким образом, дедуктивное умозаключение играет большую роль в мыслительной деятельности человека. Рассуждения принимают форму дедукции в том случае, когда частное явление подводится к общему.14

1. Сложные и сокращенные силлогизмы.

В мышлении мы оперируем понятиями, суждениями и умозаключениями, в том числе и силлогизмами. Как и суждения, силлогизм может быть простым и сложным. Сложный силлогизм состоит из нескольких простых силлогизмов. Они образуют полисиллогизм, или сложный силлогизм. Полисиллогизм представляет собой несколько соединенных между собой последовательной связью простых силлогизмов. При этом вывод, следствие одного из простых силлогизмов становится посылкой для последующего. Таким образом, получается своеобразная «цепь» силлогизмов.

Все полисиллогизмы делятся на регрессивные силлогизмы и прогрессивные.

Прогрессивный силлогизм характеризуется тем, что его заключение становится большей посылкой следующего силлогизма. Заключение регрессивного силлогизма становится меньшей посылкой в последующем.

Для простоты применения и экономии времени, а особенно в случаях, когда заключение очевидно, применяются сокращенные силлогизмы. Когда говорится о сокращенных силлогизмах, имеется в виду, что в таком умозаключении пропущена одна из посылок, а в некоторых случаях – заключение.

Все птицы имеют крылья.

Все чайки – птицы.

Все чайки имеют крылья.

Это пример простого категорического силлогизма.

Для того чтобы получить сокращенный силлогизм, можно опустить большую посылку, т.е. «все чайки имеют крылья». Таким образом, получим: «Все чайки являются птицами – значит, все чайки имеют крылья». Естественно, что в этом случае следствие силлогизма будет истинным. Другими словами, сокращение силлогизма не влияет на его истинность или ложность.

Можно привести такой пример: «Все газы летучи, следовательно, кислород летуч». Это сокращенный силлогизм, а полный выражается следующим образом.

Все газы летучи.

Кислород – газ.

Кислород летуч.

В отличие от предыдущего примера здесь пропущена меньшая посылка.
Заключение пропускается в том случае, когда нет необходимости выражать полученное следствие в силу его очевидности, явности для окружающих, которая проистекает из природы самих посылок (т.е. если посылки и связанные с ними предметы, явления достаточно хорошо известны). Например: «Все, что легче воды, в ней не тонет. Пенопласт легче воды». В данном случае пропущенный вывод достаточно очевиден. Силлогизм выглядит следующим образом.

Все, что легче воды, в ней не тонет.

Пенопласт легче воды.

Пенопласт не тонет в воде.

1. Виды индуктивных умозаключений.

Индуктивным называется умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности классу в целом.

В зависимости от полноты и законченности эмпирического исследования различают два вида индуктивных умозаключений: полную индукцию и неполную. В неполной индукции различают популярную и научную в зависимости от способа отбора исходного материала. Научная индукция делится в зависимости от способа исследования на индукцию методом отбора и индукцию методом исключения.

Полная индукция – это умозаключение, в котором на основе принадлежности каждому элементу или каждой части класса определенного признака делают вывод о его принадлежности классу в целом. Индуктивные умозаключения такого типа применяются лишь в тех случаях, когда имеют дело с закрытыми классами, число элементов в которых является конечным и легко обозримым. Например, число государств в Европе, количество промышленных предприятий в данном регионе, число субъектов федерации в данном государстве и т.п. Схема умозаключения полной индукции имеет следующий вид:

S1 имеет признак P;

S2 имеет признак P;

Sn имеет признак Р.

S1, S2, ... , Sn – составляют класс К.

Всем предметам класса K присущ признак Р.

Выраженная в посылках этого умозаключения информация о каждом элементе или каждой части класса служит показателем полноты исследования и достаточным основанием для логического переноса признака на весь класс. Тем самым вывод в умозаключении полной индукции носит демонстративный характер. Это означает, что при истинности посылок заключение будет необходимо истинным. Познавательная роль умозаключения полной индукции проявляется в формировании нового знания о классе или роде явлений.

Неполная индукция – это умозаключение, в котором на основе принадлежности признака некоторым элементам или частям класса делают вывод о его принадлежности классу в целом.

S1 имеет признак P;

S2 имеет признак P;

Sn имеет признак P.

S1, S2, ... , Sn принадлежат классу K.

Классу K, по-видимому, присущ признак P.

Неполнота индуктивного обобщения выражается в том, что исследуют не все, а лишь некоторые элементы или части класса – от S1 до Sn. Логический переход в неполной индукции от некоторых ко всем элементам или частям класса не является произвольным. Он оправдывается эмпирическими основаниями – объективной зависимостью между всеобщим характером признаков и устойчивой их повторяемостью в опыте для определенного рода явлений.

Популярной индукцией называют обобщение, в котором путем перечисления устанавливают принадлежность признака некоторым предметам или частям класса и на этой основе проблематично заключают о его принадлежности всему классу.

Научной индукцией называют умозаключение, в котором обобщение строится путем отбора необходимых и исключения случайных обстоятельств.15

1. Методы установления причинных связей.

Методы установления причинных связей составляют один из видов индукции. В качестве методологии здесь выступают положения принципа причинности. Что понимается под причиной при использовании указанных методов? Известно, что причина – это явление, которое в определенных условиях порождает другое явление, называемое следствием или действием причины. Следствие – это явление, порождаемое причиной. Что понимается под первым и вторым явлениями? Во-первых, событие, существование или несуществование предметов и т.д. (извержение вулкана – причина изменения окружающей среды; наличие вирусов в организме – причина заболевания и т.п.). Во-вторых, взаимодействие противоположных сторон предмета и изменения, происходящие в данном предмете в результате этого взаимодействия. Далее под причиной понимается обстоятельство, добавление которого к имеющимся обстоятельствам вызывает следствие – явление, представляющее собой событие, существование предмета, изменение предмета, возникновение нового свойства у предмета и т.д. Следует заметить, что рассматриваемые методы позволяют выявлять не любые причинно-следственные связи, а лишь наиболее простые из них.

При применении методов установления причинной связи в качестве научной методологии используются некоторые положения принципа причинности. В частности, полагается, что причинно-следственная связь является: объективной; необходимой (определенная причина в соответствующих условиях обязательно вызывает определенное следствие); всеобщей (в природе нет беспричинных явлений); причина предшествует следствию во времени (по крайней мере, следствие не может появиться раньше причины).16

1. Умозаключение по аналогии.

В науке и практических делах объектом исследования нередко выступают единичные, неповторимые по своим индивидуальным характеристикам события, предметы и явления. При их объяснении и оценке затруднено применение как дедуктивных, так и индуктивных рассуждений. В этом случае прибегают к третьему способу рассуждения – умозаключению по аналогии: употребляют новое единичное явление другому, известному и сходному с ним единичному явлению и распространяют на первое ранее полученную информацию.

Умозаключение по аналогии – это вывод о принадлежности определенного признака исследуемому единичному объекту (предмету, событию, отношению или классу) на основе его сходства в существенных чертах с другим уже известным единичным объектом.

Умозаключению по аналогии всегда предшествует операция сравнения двух объектов, которая позволяет установить сходства и различения между ними. При этом для аналогии требуется не любые совпадения, а сходства в существенных признаках при несущественности различий. Именно такие сходства служат основой для уподобления двух материальных или идеальных объектов.

Логический переход от известного к новому знанию регулируется в выводах по аналогии следующим правилом: если два единичных предмета сходны в определенных признаках, то они могут быть сходны в других, обнаруженных в одном из сравниваемых предметов, признаках.

По характеру уподобляемых объектов различают два вида аналогии: аналогию предметов и аналогию отношений.

Аналогия предметов – умозаключение, в котором объектом уподобления выступают два сходных единичных предмета, а переносимым признаком – свойства этих предметов.

Аналогия отношений – умозаключение, в котором объектом уподобления выступают сходные отношения между двумя парами предметов, а переносимым признаком – свойства этих отношений.

Степень обоснованности выводов по аналогии зависит от качества связи между сходным и переносимым признаком. Различают строгую и нестрогую аналогию. Строгая аналогия. Отличительная ее особенность – необходимая связь переносимого признака с признаками сходства. Нестрогая аналогия это такое уподобление, в котором зависимость между сходными и переносимыми признаками мыслится как необходимая лишь с большей или меньшей степенью вероятности. В этом случае, обнаружив у другого объекта признаки сходства, можно лишь в логически обусловленной, т.е. проблематичной, форме заключать о принадлежности ему переносимого признака.17

1. Основные формально-логические законы.

Практически в ряде учебников по логике рассматриваются десятки законов. Однако во многих учебниках среди множества логических законов принято выделять следующие четыре: закон тождества, закон противоречия, закон исключенного третьего и закон достаточного основания. Они считаются основными формально-логическими законами.

Закон тождества. Этот закон раскрывает сущность требования об определенности и однозначности наших мыслей. Закон тождества можно сформулировать следующим образом: содержание и объем мысли о каком-либо предмете должны быть строго определены и оставаться постоянными в процессе рассуждения о нем.

В соответствии с законом тождества, рассуждая о чем-либо, мы должны уточнить объем и содержание используемых нами понятий и в процессе рассуждения и вывода строго придерживаться выбранных нами вначале ограничений (параметров), не подменяя в ходе рассуждения их другими. Выполнение этого требования гарантирует нам точность, определенность, недвусмысленность наших рассуждений; создает возможность различать и отождествлять предметы в формальных системах по выражающим их терминам. Сознательное ограничение объема и содержания мыслей о различных предметах позволяет на основе закона тождества производить абстракцию их отождествления. Иначе говоря, закон тождества сводится к принципиальной однозначности понятий, используемых нами на протяжении всего рассуждения и вывода.

Закон противоречия. Условием истинного познания выступает также требование непротиворечивости мышления. Суть его раскрывается в формально-логическом законе противоречия, который можно сформулировать следующим образом: в процессе рассуждения о каком-либо определенном предмете нельзя одновременно утверждать и отрицать что-либо в одном и том же отношении, в противном случае оба суждения не могут быть вместе истинными.

Закон противоречия справедлив относительно любых видов противоположных суждений в обыденном и научном мышлении. Он играет важную роль в теории дедуктивного вывода и построении доказательства, поскольку выступает определяющим моментом в понимании и обосновании логической необходимости следования заключений из посылок. Следование заключения из посылок является логически необходимым лишь в том случае, когда при отрицании заключения мы не вступаем в противоречие с посылками умозаключения.

Закон исключенного третьего следует рассматривать как дальнейшее уточнение требований непротиворечивости, последовательности и определенности, предъявляемых к мышлению. Он должен способствовать устранению из наших рассуждений неопределенных, двусмысленных выражений, употреблению определенных вопросов и ответов в дискуссиях и т.п. Закон исключенного третьего имеет силу лишь при условии соблюдения требований ранее изложенных законов тождества и противоречия и может быть сформулирован следующим образом: в процессе рассуждения необходимо доводить дело до определенного утверждения или отрицания, в этом случае истинным оказывается одно из двух отрицающих друг друга суждений. Этим законом исключается истинность какого-либо третьего суждения, кроме того суждения, к которому мы пришли, или его отрицания. Здесь предлагается сделать выбор из двух противоречащих друг другу суждений. Одно из них должно быть непременно истинным. При этом закон не указывает, какое именно из суждений истинно, но указывает, что  истина лежит лишь в пределах этих двух суждений, а не какого-то третьего. Закон исключенного третьего имеет силу относительно любых пар суждений, в которых одно утверждает то, что отрицается в другом. 

Закон достаточного основания. Важным условием правильного мышления является также свойство доказательности. Это свойство мысли выражается в законе достаточного основания, который формулируется следующим образом: в процессе рассуждения достоверными следует считать лишь те суждения, относительно истинности, которых могут быть приведены достаточные основания. Рассуждение, в котором истинность некоторого положения не просто утверждается, но указываются основания, в силу которых мы не можем не признать его истинным, следует считать доказательным. При этом под достаточными основаниями истинности некоторого суждения понимается совокупность обязательно истинных других суждений, из которых первое следует с логической необходимостью. В состав этих истинных суждений могут входить аксиомы, определения, суждения непосредственного восприятия, истинность которых установлена опытным путем; суждения, истинность которых доказана с помощью других истинных суждений.

Выделение этих законов в качестве основных определяется тем, что в них формулируются наиболее общие и необходимые условия не только логической правильности каждой конкретной связи между суждениями и понятиями, но и самой возможности мышления как познавательной деятельности.

1. Доказательство и опровержение.

Невозможно переоценить значение доказательств в нашей жизни и особенно в науке. К доказательствам прибегают все, но редко кто задумывается над тем, что означает «доказать», почему доказательство «доказывает», всякое ли утверждение можно доказать или опровергнуть, все ли нужно доказывать и т.п.

Под доказательством в логике понимается процедура установления истинности некоторого утверждения путем приведения других утверждений, истинность которых уже известна и из которых с необходимостью вытекает первое. В доказательстве различаются тезис – утверждение, которое нужно доказать, основание (аргументы) – те положения, с помощью которых доказывается тезис, и логическая связь между аргументами и тезисом. Понятие доказательства всегда предполагает, таким образом, указание посылок, на которые опирается тезис, и тех логических правил, по которым осуществляются преобразования утверждений в ходе доказательства.

Доказательство – это правильное умозаключение с истинными посылками. Логическую основу каждого доказательства (его схему) составляет логический закон. Доказательство – это всегда в определенном смысле принуждение. Источником «принудительной силы» доказательств являются логические законы мышления, лежащие в их основе. Именно данные законы, действуя независимо от воли и желаний человека, заставляют в процессе доказательства с необходимостью принимать одни утверждения вслед за другими. Задача доказательства – исчерпывающе утвердить обоснованность доказываемого тезиса.

Раз в доказательстве речь идет о полном подтверждении, связь между аргументами и тезисом должна носить дедуктивный характер. По своей форме доказательство – дедуктивное умозаключение или цепочка таких умозаключений, ведущих от истинных посылок к доказываемому положению.

Обычно доказательство протекает в очень сокращенной форме.

Образцом доказательства, которому в той или иной мере стремятся следовать во всех науках, является математическое доказательство. Математическое доказательство является парадигмой доказательства вообще, но даже в математике доказательство не является абсолютным и окончательным.

Опровержение – это рассуждение, направленное против выдвинутого тезиса и имеющее целью установление его ложности или недоказанности. Распространенный прием опровержения – выведение из опровергаемого утверждения следствий, противоречащих истине. Хорошо известно, что если даже одно-единственное логическое следствие некоторого положения ложно, то ложным является и само положение. Другой прием установления ложности тезиса – доказательство истинности его отрицания. Утверждение и его отрицание не могут быть одновременно истинными. Как только удается показать, что верным является отрицание тезиса, вопрос об истинности самого тезиса автоматически отпадает. Достаточно, скажем, показать одного белого медведя, чтобы опровергнуть убежденность в том, будто медведи бывают только бурыми. Если утверждается, что у каждой планеты во Вселенной есть спутники, стоит указать одну планету без спутников (скажем, Венеру), чтобы опровергнуть это утверждение.

Эти два приема применимы для опровержения любого тезиса, независимо от того, снабжен он какими-то поддерживающими его аргументами или нет.

Если тезис выдвигается с каким-то обоснованием, операция опровержения может быть направлена также против обоснования. В этом случае нужно показать, что приводимые аргументы ложны или несостоятельны.

Ошибочность аргументов выявляется так же, как и ошибочность тезиса: выведением из них следствий, оказывающихся в итоге несостоятельными, или доказательством утверждений, противоречащих аргументам.

Следует иметь в виду, что дискредитация доводов, приводимых в поддержку какого-то положения, не означает еще неправильности самого этого положения. Утверждение, являющееся по сути дела верным, может отстаиваться с помощью случайных или слабых аргументов.

Опровержение может быть направлено, наконец, на саму связь аргументов и тезиса. В этом случае надо показать, что тезис не вытекает из доводов, приведенных в его подтверждение. Если между аргументами и тезисом нет логической связи, то нет и доказательства тезиса с помощью приводимых аргументов. Из этого не вытекает, конечно, ни то, что аргументы ошибочны, ни то, что тезис ложен.18

Список, использованной литературы:

1. Логика: Учебное пособие / В.К. Батурин. – М.: КУРС: НИЦ Инфра-М, 2012. 
2. Логика: Учебное пособие / Е.Б. Ерина. – 2-e изд. – М.: ИЦ РИОР: ИНФРА-М, 2012.
3. Логика: Учебник / И.В. Демидов; Под ред. Б.И. Каверина. – 7-e изд., испр. – М.: Дашков и К, 2012. 
4. Логика и методология науки: Современное гуманитарное познание и его перспективы: Учебное пособие / А.В. Павлов; Министерство образования и науки РФ – М.: Флинта: Наука, 2013.
5. Логика: Учебник / В.И. Кириллов. – М.: НОРМА, 2013.
6. Логика: Учебник / Ивин А.А. – М.: Высшая школа, 2011.
7. Логика: Конспект лекций / Д. Шадрин. – М.: Эксмо, 2011.

1 Логика: Учебник / В.И. Кириллов. – М.: НОРМА, 2013, стр. 44–48.

2 Логика: Учебник / И.В. Демидов; Под ред. Б.И. Каверина. – 7-e изд., испр. – М.: Дашков и К, 2012, стр. 66. 

3 Логика: Учебное пособие / Е.Б. Ерина. – 2-e изд. – М.: ИЦ РИОР: ИНФРА-М, 2012, стр. 19–21.

4 Логика: Учебник / И.В. Демидов; Под ред. Б.И. Каверина. – 7-e изд., испр. – М.: Дашков и К, 2012, стр. 71–72. 

5 Логика: Учебник / В.И. Кириллов. – М.: НОРМА, 2013, стр. 61–69.

6 Логика: Учебное пособие / В.К. Батурин. – М.: КУРС: НИЦ Инфра-М, 2012 стр. 44. 

7 Логика: Учебник / И.В. Демидов; Под ред. Б.И. Каверина. – 7-e изд., испр. – М.: Дашков и К, 2012, стр. 113–114. 

8 Логика: Учебное пособие / В.К. Батурин. – М.: КУРС: НИЦ Инфра-М, 2012 стр. 49. 

9 Логика: Учебное пособие / Е.Б. Ерина. – 2-e изд. – М.: ИЦ РИОР: ИНФРА-М, 2012, стр. 33–34. 

10 Логика: Учебное пособие / В.К. Батурин. – М.: КУРС: НИЦ Инфра-М, 2012, стр. 46–47.

11 Логика: Конспект лекций / Д. Шадрин. – М.: Эксмо, 2011.

12 Логика: Учебное пособие / В.К. Батурин. – М.: КУРС: НИЦ Инфра-М, 2012, стр. 49–50.

13 Логика: Учебное пособие / Е.Б. Ерина. – 2-e изд. – М.: ИЦ РИОР: ИНФРА-М, 2012, стр. 58–59. 

14 Логика: Учебник / И.В. Демидов; Под ред. Б.И. Каверина. – 7-e изд., испр. – М.: Дашков и К, 2012, стр. 185–190. 

15 Логика: Учебное пособие / Е.Б. Ерина. – 2-e изд. – М.: ИЦ РИОР: ИНФРА-М, 2012, стр. 72–77.

16 Логика: Учебник / Ивин А.А. – М.: Высшая школа, 2011.