ХАРАКТЕРИСТИКИ СИСТЕМ І ОБЄКТІВ АВТОМАТИЧНОГО УПРАВЛІННЯ

3 ХАРАКТЕРИСТИКИ СИСТЕМ І ОБ'ЄКТІВ АВТОМАТИЧНОГО УПРАВЛІННЯ

3.1. Типові динамічні впливи і основні характеристики

В техніці є дві важливі задачі: перша - оцінка якості систем і об'єктів і друга - створення таких систем, що відповідають необхідним критеріям. Перша задача виникає при аналізі вже існуючих систем, друга - при проектуванні нових у відповідності до технічного завдання. В обох випадках необхідно забезпечити об'єктивність оцінки і порівняння систем поміж собою.

Системи, як правило, оцінюються за критерієм, що визначається з їх функціонального призначення. Так, для САУ металорізного устаткування найважливішим критерієм є точність відтворення різних законів руху, точність обробки, точність позиціювання, точність досягнення прийнятого критерію оптимальності тощо. В умовах промислової експлуатації на САУ діє принаймні один керуючий вплив і одне збурення, а оцінка проводиться за ступенем відповідності вихідної величини (цілі управління) закону, що вимагається. Оскільки в цьому випадку точність відтворення буде залежати як від параметрів самої САУ, так і від модифікації законів, що задаються і що збурюють, які заздалегідь не визначені, виділити вплив безпосередньо системи на загальному фоні дуже важко.

Наприклад, для оцінки точності гідравлічного супорта за обробленою деталлю (розмір у на рис. 3.1), необхідно враховувати закон модифікації управляючого впливу x(t), що визначається профілем копира К і повздовжньою подачею S, а також з усіх діючих збурень хоча б одне - складову Ру сили різання.

Таким чином, два однакові гідравлічні супорти, які працюють в різних умовах, тобто при різних керуючих впливах та збуреннях, забезпечують різну точність обробки.

Тому для забезпечення об'єктивної оцінки САУ користуються спеціальними однаковими сигналами, що подаються на вхід системи. Ці сигнали називають типовими динамічними впливами. При дослідженні САУ прагнуть вибрати такий вплив, реакція на який достатньо повно відображає як статичні, так і динамічні характеристики системи. Крім того, враховується вимога простоти відтворення такого впливу. Цим вимогам якнайбільше відповідають наступні типові динамічні впливи: східчаста функція, імпульсна функція і гармонічний сигнал.

Одинична східчаста функція.

На вхід системи подають сигнал у вигляді одиничної східчастої функції (інші назви - одиничний стрибок або функція Хевісайда):

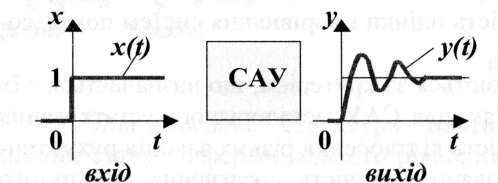
Рис.3.2. Одинична східчаста функція і перехідна характеристика

При цьому припускається, що одиниця має ту ж вимірність, що і фізична величина на вході системи. Реакція системи на одиничну східчасту функцію називається перехідною характеристикою (рис.3.2).

На практиці такий типовий сигнал легко реалізується, наприклад при різкому збільшенні глибини різання, при ввімкненні САУ, при різкому збільшенні навантаження тощо. Єдиною умовою є висока швидкість наростання сигналу - вона повинна наближатися до ідеальної величини, тобто до нескінченості.

Одинична імпульсна функція.

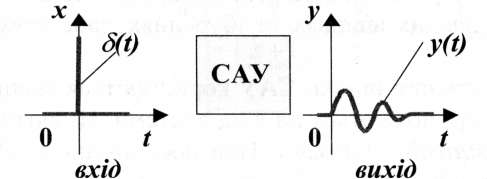
На вхід системи подають сигнал у вигляді одиничної імпульсної функції (інші назви - одиничний імпульс або функція Дірака):

Рис.3.3. Одинична імпульсна функція і вагова характеристика

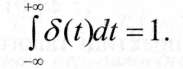
Одиничний імпульс є похідною від одиничної ступінчастої функції, а називається він одиничним тому, що:

Реакція системи на одиничний імпульс називається ваговою характеристикою, або характеристикою ваги (рис.3.3). Для лінійних систем вагова характеристика є похідною від перехідної характеристики. Практичне значення такої характеристики полягає у тому, що вона дозволяє оцінити якість системи, яка функціонує (тобто провести її ідентифікацію) при прикладення до каналу управління, бо не викликає зсув основного сигналу (на відміну від одиничної ступінчастої функції) за цим каналом і не порушує функціонування системи, що тестується.

Перехідна і вагова характеристики будуються у просторі: вихідна величина - час, тому вони ще називаються часовими характеристиками.

Гармонічний сигнал.

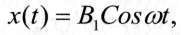
Використання типового гармонічного впливу передбачає подачу на вхід САУ або об'єкта гармонічного сигналу

де В1 - амплітуда, - кругова частота (див. рис. 3.4

Рис. 3.4. Гармонічний сигнал і реакція системи

На виході лінійної САУ або об'єкту в режимі, що встановився, буде також

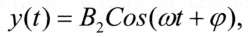
гармонічний сигнал

де =360°/ - фазовий кут.

Реакція САУ на гармонічний вплив подається двома частотними характеристиками: амплітудно-частотною і фазово-частотною. Амплітудно-частотна характеристика (АЧХ) показує, як змінюється відношення амплітуди вихідного сигналу до амплітуди вхідного у функції частоти:

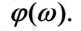
Фазово-частотна характеристика (ФЧХ) показує залежність фазового
кута від частоти:

Для прикладення на практиці такого сигналу до системи чи об’єкта необхідний спеціальний пристрій - генератор гармонічного сигналу, причому цей сигнал повинен перетворюватись у фізичну величину, що сприймається системою. Але, не зважаючи на деякі практичні складнощі у порівнянні з попередніми впливами, гармонічний сигнал широко застосовується тому, що дозволяє отримати набагато більше інформації до ідентифікації систем.

3.2. Частотні характеристики

На етапі аналізу і синтезу систем і об'єктів, що проектуються, визначити їх частотні характеристики можна за відомими передаточним функціями. Для цього здійснюють перехід до частотних передаточних функцій, які отримують зі звичайних заміною оператора s на]:

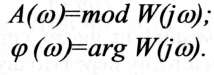
Отже, частотна передаточна функція W(jco) є комплексним числом, модуль якого відповідає АЧХ, а аргумент - ФЧХ. Таким чином, справедливі співвідношення:

Очевидно, що задача аналітичного визначення частотних характеристик на етапі аналізу проектного рішення зводиться до визначення комплексного виразу (/) і виділення в ньому модуля і аргументу. Це неважко зробити, коли відомі дійсна () = Re [W(jco)] і уявна () = Іт [W(jco)] частини частотної передаточної функції W(jco) = () + jV(co) (див. рис. 3.6). У цьому випадку користуємось співвідношеннями:

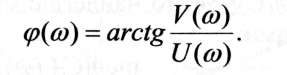
Звичайно частотна передаточна функція подається у вигляді відношення двох поліномів і для виділення дійсної і уявної частин застосовують відомий прийом: множать чисельник і знаменник на поліном, спряжений до знаменника.

Якщо частотна передаточна функція має вигляд співвідношення двох поліномів: W(j(o) = С!^)/С20о)), то найлегше можна знайти АЧХ і ФЧХ, користуючись залежностями:

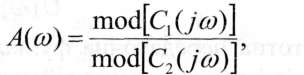
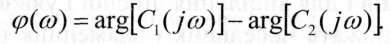
Із залежностей (3.5) випливає, що АЧХ і ФЧХ можуть бути об'єднані в одну характеристику - АФЧХ (амплітудно-фазово-частотна характеристика), яка будується на комплексній площині (рис. 3.6).

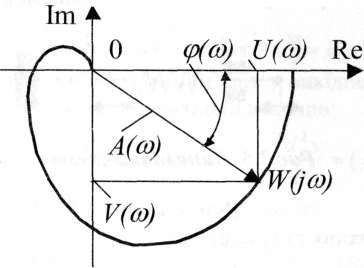
АФЧХ являє собою годограф радіус-вектора частотної передатної функції при модифікації частоти від 0 до оо.

Рис.3.6. Амплітудно-фазова частотна характеристика

На графіку АФЧХ, що називають також діаграмою Найквіста, обов'язково виділяють точки, біля яких пишуть значення відповідних частот.

Для спрощення побудови і перетворення частотних характеристик, а саме, амплітудних, застосовують логарифмічні частотні характеристики

Логарифмічна АЧХ (ЛAЧX) вимірюється в децибелах (дБ). Бел - логарифмічна одиниця відношення двох однойменних фізичних величин - названа на честь винахідника телефону Олександра Бела. Однак, ЛAЧX можуть умовно розраховуватися і для відношення різних фізичних величин входу і виходу системи. З (3.8) випливає, що один децибел відповідає надто малій зміні амплітуди. Дійсно, при зміні JIA4X в 1 дБ амплітуда змінюється в ~ 1,122 рази.

Логарифмічні частотні характеристики будують у напівлогарифмічній системі координат. Враховуючи, що для більшості САУ фазово- частотна характеристика, як правило, негативна, зручно вести побудову в суміщеній системі координат для Л АЧХ і Л ФЧХ (рис. 3.7).

По осі абсцис відкладають логарифм частоти, вказуючи вимірність (рад/с або Гц). Діапазон зміни частоти в 10 разів називають декадою. По осі ординат відкладають значення L(co) у дБ (праворуч) і значення () у градусах (ліворуч).

Рис. 3.7. Система координат для побудови Л АЧХ і ЛФЧХ

Для ілюстрації спрощення побудови ЛАЧХ розглянемо наступні приклади.

1. Якщо () = k0, тоді L(co) = 20 lg к0 і ЛАЧХ представляється прямою, що паралельна вісі частот на відстані 20 lg к0 - пряма 1 на рис.3.7.

2. Якщо А(со) = к0 /, тоді L(w) = 20 lg (к0 /) = 20 lg к0 - 20 Igco і ЛАЧХ представляється прямою, що проходить через точку з координатами [ = 1, L(co) = 20 lg к0 ] під нахилом -20 дБ/дек, оскільки збільшення частота у 10 разів викликає зменшення логарифмічної амплітуди на 20 дБ - пряма 2 на рис.3.7.

3. Якщо () = к0 со, тоді L(co) = 20 lg (k0 ) = 20 lg k0 + 20 Igco і ЛАЧХ представляється прямою, що проходить через точку з координатами [ = 1, L(co) =20 lg к0 ] під нахилом +20 дБ/дек, оскільки збільшення частоти у 10 разів викликає збільшення логарифмічної амплітуди на 20 дБ - пряма 3 на рис.3.7.

Розглянемо методику побудови таких асимптотичних логарифмічних частотних характеристик на прикладі системи з передаточною функцією W(s) = k/(Ts+l). У прикладі, що розглядався раніше, були отримані залежності для АЧХ і ФЧХ такої системи. Скориставшись ними, з урахуванням формули (3.8), знаходимо логарифмічну частотну характеристику:

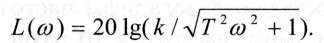
Побудову проводять у напівлогарифмічній сітці (рис.3.8) наступним чином. Для частот < 1/Т знаменник АЧХ близький до одиниці, а для > 1/Т одиницею під знаком кореня у знаменнику можна знехтувати. Тому

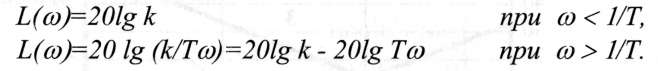
Частота сос=1/Т називається спряженою частотою. Побудову асимптот виконують згідно з отриманими залежностями: через спряжену частоту проводять вертикальну лінію і до цієї межі JIA4X зображається прямою, паралельною осі частот на відстані 20lg к, а за межею - прямою з нахилом -20 дБ/дек.

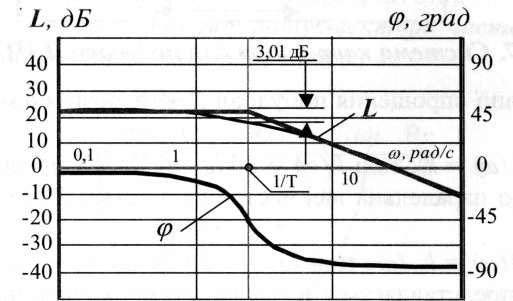
Рис. 3.8. Логарифмічні частотні характеристики

Побудована таким чином асимптотична характеристика (рис. 3.8) відрізняється від дійсної. Максимальна відмінність у точці 0=1/ та становить 3,01 дБ.

В деяких випадках при синтезі систем з використанням частотних методів зручно користуватися логарифмічною АФЧХ, яку називають також діаграмою Блека. Ця характеристика, так само як і АФЧХ, будується шляхом об'єднання JIA4X і ЛФЧХ на одній координатній сітці. На рис. 3.9 показана діаграма Блека для системи, що має логарифмічні частотні характеристики, наведені на рис. 3.8.

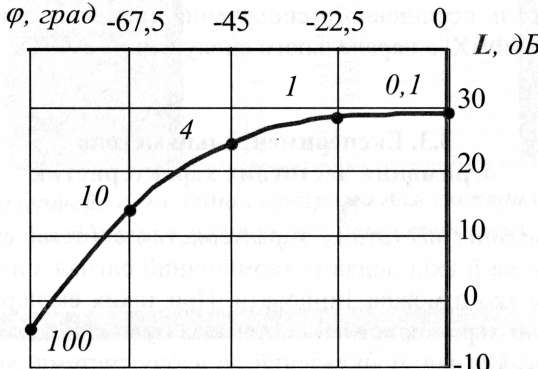
Рис. 3.9, Логарифмічна АФЧХ - діаграма Блека

Тут, як і на графіку АФЧХ, обов'язково занотовують значення частот біля контрольних точок

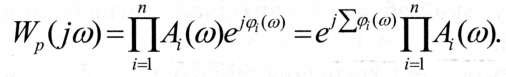
Достоїнство ЛАЧХ полягає також і в тому, що вони дозволяють просто будувати частотні характеристики складних систем за відомими ЛАЧХ елементів, які складають систему. Відомо, що послідовне з'єднання елементів зводиться до одного елемента з передаточною функцією (2.39). Отже, результуюча частотна передаточна функція послідовного з'єднання елементів матиме такий вигляд:

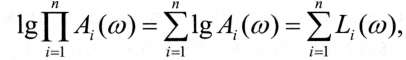
З формули (3.10) видно, що при побудові частотних характеристик послідовного сполучення елементів необхідно додавати графіки їх ФЧХ і перемножити АЧХ. Однак, оскільки

то побудова результуючої ЛАЧХ також зводиться до додавання графіків. Результуючу частотну передаточну функцію паралельного сполучення элементів легше знайти, якщо представити передаточні частотні функції елементів у вигляді:

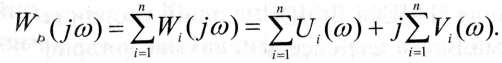
Тоді відповідно до результуючої передаточної функції паралельного з’єднання елементів, знаходимо:

Аналіз залежностей (3.10) і (3.11) показує, що при побудові частотних характеристик Послідовного сполучення елементів доцільно користуватися ЛАЧХ і ЛФЧХ, а паралельного сполучення - АФЧХ.

ХАРАКТЕРИСТИКИ СИСТЕМ І ОБЄКТІВ АВТОМАТИЧНОГО УПРАВЛІННЯ