ПОБУДОВА ПЛАНІВ ШВИДКОСТЕЙ ДЛЯ ГРУП 2 КЛАСУ, ЩО МІСТЯТЬ ПОСТУПАЛЬНІ ПАРИ

ТЕМА N8

1. ПОБУДОВА ПЛАНІВ ШВИДКОСТЕЙ ДЛЯ ГРУП 2 КЛАСУ, ЩО МІСТЯТЬ ПОСТУПАЛЬНІ ПАРИ.

1.1. Визначення лінійних і кутових швидкостей.

Розглянемо структурну групу 2 класу 2 виду (рис.1,а) яка включає одну поступальну пару D і дві послідовно розташовані обертальні пари В и С. Ланка 2 входить в обертальну пару В з ланкою 1, що належить основному механізму, а ланка 3 входить у поступальну пару D з ланкою 4 приналежній також основному механізму.

а) в)

Рис. 1.

Відомими є вектор швидкості Vв точки В и вектори швидкостей усіх точок, що належать ланці 4. Отже, відома і кутова швидкість ланки 4.

Ланка 3 у відносному русі ковзає по осі X-X напрямній, що належить ланці 4. Покажемо ланку 4 у вигляді площини S і позначимо точку площини S, що співпадає для заданого положення з точкою С через С4.

Вектор швидкості Vс4 точки С4, яка належить ланці 4 відомий. Тоді для визначення Vс - вектора швидкості точки С - необхідно вирішити систему векторних рівнянь:

; (1)

. (2)

У цих рівняннях вектори VВ і Vс4 швидкостей точок В и С4 відомі за величиною і напрямком. Вектори Vc4 швидкості точки С щодо ланки 4, і VСВ - швидкості точки С відносно точки В - відомі лише за напрямком.

Для побудови плану швидкостей вибираємо довільну точку р за полюс плану швидкостей і відкладаємо від її відомі вектори VВ і Vc4 швидкостей точок В и С4 у вигляді відрізків (рb) і (рс4), що зображують у обраному масштабі ці швидкості. Далі через точку (в) проводимо пряму в напрямку вектора швидкості VСВ, перпендикулярну до напрямку СВ (рис.1,б), а через точку С4 проводимо пряму в напрямку вектора VСС4 відносної швидкості, паралельну до осі X - X поступальної пари D.

Точка перетинання цих напрямків і дасть кінець вектора Vc швидкості точки С. Величина швидкості Vc визначається за формулою

. (3)

Швидкості інших точок ланки і кутова швидкість ланки 2 визначаються так само як у раніше розглянутому випадку. Кутова швидкість ланки 3, що входить з ланкою 4 у поступальну пару, має ту ж кутову швидкість що і ланка 4, тобто

(4)

Для визначення швидкості якої-небудь довільної точки F ланки 3 (рис.1, а) можна скористатися векторним рівнянням

(5)

Вектор швидкості точки F4, що належить площині S, тобто ланці 4 нам відомий. Відносна швидкість VF3F4 дорівнює швидкості Vc3c4, через те, що ланка 3 відносно ланки 4 рухається поступально, отже, швидкості всіх точок ланки 3 відносно ланки 4 рівні між собою. Тому рівняння (5) може бути переписане так:

(6)

Відповідно рівнянню (6) з точки F4 (рис.1,б) проводимо відрізок (f4f), рівний и паралельний відрізку (c4c). Результуючий відрізок (pf3) i являє собою в масштабі абсолютну швидкість точки F3, :

(7)

7.2. ВИЗНАЧЕННЯ ЛІНІЙНИХ І КУТОВИХ ПРИСКОРЕНЬ.

Визначення прискорень групи 2 класу 2 виду виконуємо аналогічно рішенню задачі про швидкості, тобто припускаємо, що відомими є прискорення точки B (рис.7.2,а) і прискорення всіх точок ланки 4, а отже, і кутове прискорення ланки 4.

а) б)

Рис.7.2.

З'єднуємо з ланкою 4 площину S і знаходимо на цій площині точку С4, що співпадається в даному положенні з точкою С. Відомими є вектори прискорень точок В і С4.

Прискорення точки С визначаємо з рівнянь

(8)

(9)

де - прискорення Коріоліса;

- відносне (релятивне) прискорення.

Відносне (релятивне) прискорення являє собою прискорення точки С відносно площини S, що належить ланці 4. Через те що вісь X - X напрямної разом із площиною S має складний обертально-поступальний рух, то, крім відносного прискорення в рівняння (9) входить і прискорення Коріоліса.

У рівняннях (8), (9) вектор прискорень точок В і С4 відомі.

Величину нормального прискорення точки С відносно В визначаємо за формулою

(10)

Вектор нормального прискорення спрямований паралельно напрямку СВ (від точки С до точки В). Величину прискорення Коріоліса визначаємо за формулою

(11)

Напрямок вектора прискорення Коріоліса визначаємо поворотом вектора відносної швидкості на 90 градусів за напрямком кутової швидкості ланок, що утворюють поступальну кінематичну пару (правило Жуковського).

Вектори тангенціального і релятивного прискорень відомі лише за напрямком: вектор тангенціального прискорення орієнтований перпендикулярно СВ, вектор релятивного прискорення орієнтований паралельно напрямній X – X.

Для їх визначення будуємо план прискорень. Для цього (рис.2,б) обираємо довільну точку за полюс плану прискорень і відкладаємо від неї відомі прискорення точок В і С4 у вигляді відрізків (b) и (с4), що являють собою в обраному масштабі прискорення точок В і С4.

Далі визначаємо за формулами (10), (11) нормальне та прискорення Коріоліса і відкладаємо їх у масштабі як відрізки (bn) і (с4k). З точок и k проводимо прямі, що мають напрямки тангенціального і релятивного прискорень. Точка С перетину цих двох напрямків і дасть кінець вектора прискорення точки С.

Величина повного прискорення точки С дорівнює

(12)

Визначаємо величину кутового прискорення ланки 2

(13)

Напрямок цього прискорення визначається так само як і в раніше розглянутій групі. Кутове прискорення ланки 3 за величиною і напрямком дорівнює кутовому прискоренню ланки 4 (тому що ці ланки утворять поступальну пару).

Прискорення будь-якої точки ланки 2 визначається за правилом подібності. Прискорення довільної точки F3 ланки 3 може бути визначене з рівняння

(14)

Прискорення точки F4, що належить площині S, відоме, тому що прискорення всіх точок ланки 4 є заданими.

Прискорення Коріоліса визначаємо аналогічно (11):

(15)

через те що

Це прискорення дорівнює прискоренню Коріоліса точки С відносно С4, тому що відносні швидкості цих точок рівні. Релятивні прискорення точки F відносно F4 і точки С відносно С4 також однакові тому що рух ланки 3 відносно ланки 4 є поступальним. Тоді рівняння (15) запишемо так:

(16)

Вектори, що знаходяться у правій частині рівняння (16) відомі, і, отже вектор прискорення точки F3 визначиться як їх геометрична сума. Для визначення цього вектора з точки f4 (рис.2,б) проводимо відрізок (f 4), рівний і паралельний відрізку (с4k). Далі з точки проводимо відрізок (f), рівний и рівнобіжний відрізку (kc). результуючий відрізок (f3) і являє собою в масштабі повне прискорення точки F:

(17)

Вище ми розглянули докладно задачі про побудову швидкостей і прискорень груп 2 класи першого і другого видів. Складання рівнянь і побудова планів швидкостей і прискорень груп 2 класи інших видів буде аналогічним.

3. Приклад. На рис.3 показаний чотириланковий кулісний механізм 2 класу, довжини ланок якого відомі. Потрібно визначити швидкості і прискорення ланок механізму, якщо кривошип 1 обертається з постійною кутовою швидкістю.

Механізм утворений приєднанням до кривошипа 1 структурної групи 2 класи 2 виду, що складається з ланок 2, 3, тобто структурна група Ассура 2, 3 приєднана своїми повідцями до механізму 1 класу (ланка 1 і стояк).

3.1. ВИЗНАЧЕННЯ ЛІНІЙНИХ І КУТОВИХ ШВИДКОСТЕЙ

За заданим значенням кутової швидкості ланки 1 і його довжині визначаємо лінійну швидкість точки В

(18)

Далі складемо систему рівнянь для визначення швидкості точки B3 структурні групи. У точці B варто розрізняти три точки: B1 - належить ланці 1; В2 - ланці 2; В3 - ланці 3.

Точки В1 і В2 можна розглядати сумісно В1,2 (ланки 1 і 2 входять в обертальну кінематичну пару В, тобто швидкості та прискорення точок B1 і В2 за величиною і напрямком однакові між собою у всіх положеннях механізму.

а) б) с)

Рис. 3.

Точка В3 належить ланці 3 (кулісі) и лише геометрично співадає з точкою В1,2, тому її швидкість і прискорення будуть відрізнятись від швидкості та прискорення точки В1,2.

Тому визначимо швидкість точки В3 , що належить кулісі через дві відомі точки В1,2 и т. С. Швидкість и прискорення точки С дорівнюють нулю

( точка С належить стояку).

(19)

(20)

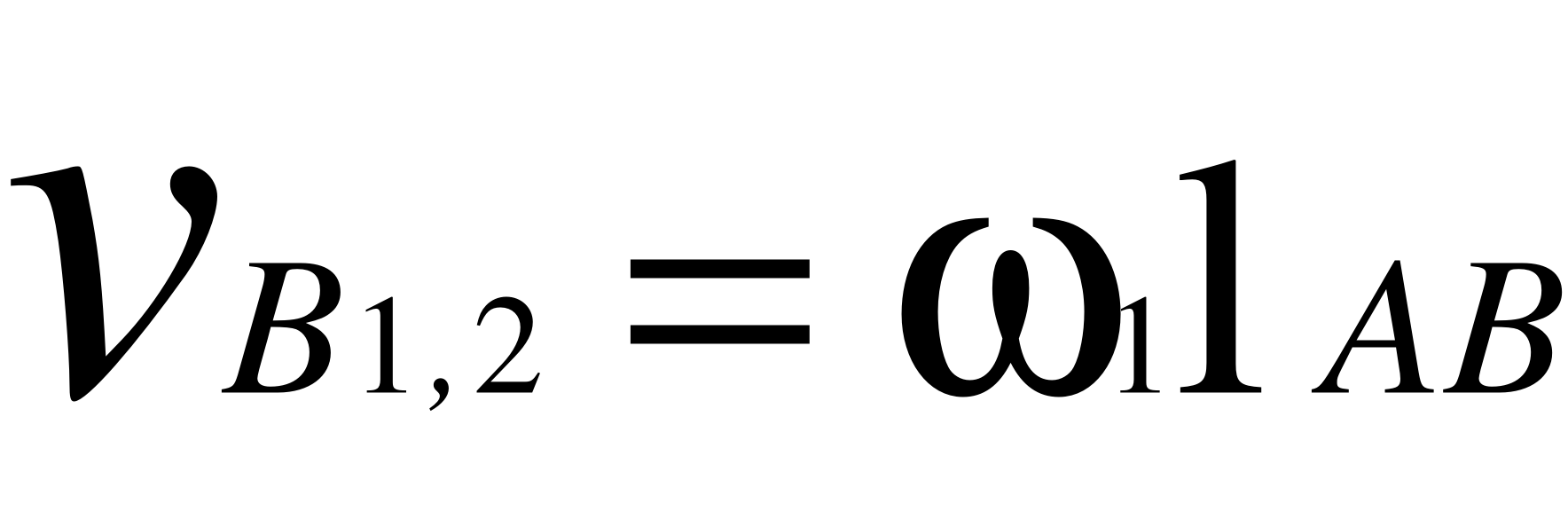
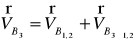
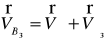
Будуємо план швидкостей (рис.3,б) у довільно обраному масштабі

Швидкість точки D визначаємо використовуючи властивість подібності за двома відомими точками C і В3.

Визначаємо кутову швидкість куліси (ланка 3)

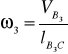
(21)

Напрямок кутової швидкості куліси визначаємо паралельним перенесенням вектора швидкості точки В3 в однойменну точку на плані механізму.

7.3.2. ВИЗНАЧЕННЯ ЛІНІЙНИХ І КУТОВИХ ПРИСКОРЕНЬ.

Прискорення точки В1,2 буде лише нормальним (доцентровим), тому що кутова швидкість кривошипа за завданням - постійна.

(22)

Запишемо систему рівнянь для визначення прискорення точки В3 (через дві відомі точки С и В1,2 ). Точка В3 буде зазнавати відносно точки В1,2 прискорення Коріоліса и релятивне (ці точки належать ланкам, що утворюють поступальну пару), а відносно точки С - нормальне і тангенціальне.

(23)

(24)

Будуємо в довільному масштабі план прискорень (рис.3,с).

Прискорення точки D визначаємо побудовою подібної фігури (у даному випадку прямої (сВ3d). Завдяки тому, що точка С належить стояку, швидкість, а також прискорення її дорівнюють 0, отже на плані швидкостей и прискорень точка С знаходиться в полюсі.

Запишемо формули для визначення абсолютних прискорень точок В3, D:

(25)

(26)

де (b3), (d) - довжини векторів прискорень точок В3, D, які взято з плану прискорень, мм.

Визначаємо тангенціальне прискорення точки В3 відносно точки С.

(27)

Використовуючи значення тангенціального прискорення точки В3 визначимо кутове прискорення куліси (ланка 3)

(28)

Напрямок кутового прискорення ланки 3 визначаємо паралельним переносом вектора тангенціального прискорення в точку В3.

3.3. Приклад для самостійного аналізу. Розглянемо схему кривошипно-повзунного механізму (рис. 4), що містить кривошип 1, з'єднаний за допомогою обертальної кінематичної пари А зі стояком 4, шатун 2, що з'єднаний обертальною парою В з кривошипом, а парою С с повзуном 3, установленому на горизонтальній напрямній X - X.

Механізм перетворює обертальний рух кривошипу (вхідна ланка) у зворотно-поступальний рух повзуна (вихідна ланка).

Вихідними даними є закон руху кривошипа (1= const) и розміри всіх ланок механізму L1, L2, ексцентриситет е. Кривошип є також и початковою ланкою.