Асимптотика решения дифференциального уравнения в окрестности бесконечно удаленной точки
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
высшего профессионального образования
«Кубанский государственный университет»
(ФГБОУ ВПО «КубГУ»)
Кафедра функционального анализа и алгебры
ДИПЛОМНАЯ РАБОТА
Асимптотика решения дифференциального уравнения в окрестности бесконечно удаленной точки
Работу выполнила ______________________Юлия Андреевна Лихарева
Факультет математики и компьютерных наук, группа 41
Специальность 010100.62 Математика
Научный руководитель ___________________ М.В.Цалюк
канд. физ.-мат. наук, доцент
Нормоконтролер ___________________ Ю.А. Лихарева
лаборант
Краснодар2015
СОДЕРЖАНИЕ
Введение.............................................................................................................3
- Глава 1
- Вспомогательные сведения................................................................4
2. Глава 2.........................................................................................................12
2.1. Случай .................................................13
2.2. Случай.................................................19
2.3. Случай ..................................................21
2.4. Случай .......................................
3. Глава 3
3.1. Случай ........................
3.2. Случай ........................
Список использованной литературы.............................................................25
ВВЕДЕНИЕ
В данной работе рассматривались линейные дифференциальные уравнения второго порядка вида

Так как совершенного невозможно дать полный обзор всего известного о свойствах решений этого уравнения, то необходимо показать различные теоремы и методы наиболее интересные для рассмотрения.
Хотя некоторые из результатов, полученных мной, являются лишь частными случаем общих теорем, все же большинство из них тесно переплетаются с темой моей работы, в частности дифференциальным уравнением второго порядка. Далее все доказательства будут представлены непосредственно для уравнения вида (1).
Курсовая работа содержит 4 главы.
В первой главе представлены некоторые теоремы, которые обуславливают ограниченность решения дифференциального уравнения второго порядка для простого случая. Во второй главе я попробую доказать ограниченность решения уравнения для случаев
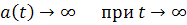
,
и найти асимптотический вид решения для уравнения (1) при.
В третьей главе я попытаюсь сформулировать теорему существования решения для уравнения вида
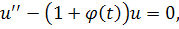
и найти асимптотический вид решения при условии
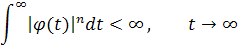
Глава 1
1 Вспомогательные сведения
В этом пункте собраны все те леммы, которые нам понадобятся в последующем.
Определение 1.1Линейным уравнением ого порядка называется
уравнение вида
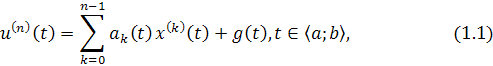
где функции называются коэффициентами уравнения, а–его свобод ным членом. Всюду ниже предполагается, что коэффициенты и его свобод ный член являются непрерывными на.
Если свободный член , то уравнение называется однородным, в противном случае неоднородным.
Лемма 1.1 Пусть и выполнено неравенство

тогда
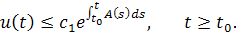
Доказательство
Пусть существует оценка
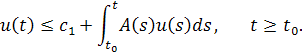
Докажем, что 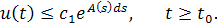
Обозначим, тогда
В силу неравенства(1.2) получим
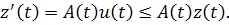
Разделим обе части наи так как , получим
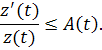
Проинтегрируем при
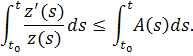
Отсюда
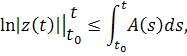
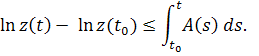
Так как , то

Потенцируем
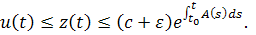
Так как
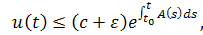
и, в силу произвольности , справедливо неравенство

Определение 1.2. Функция, которая при каждом фиксированном s как функция t является решением однородного уравнения (1.1), удовлетворяю щим начальным условиям
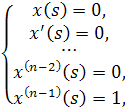
называется функцией Коши или импульсивной функцией уравнения (1.1).
Определение 1.3Пусть- два линейно независимых решения уравнения
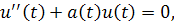
тогда их определителем Вронского или вронскианом называют определитель вида
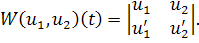
Лемма1.2 Пусть два линейно независимых решения уравнения
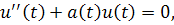
для которых определитель Вронского
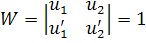
для всех . Тогда общее решение неоднородного уравнения
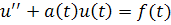
задаетсяформулой
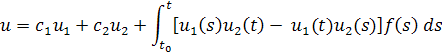
где постоянные, определяемые начальными условиями.
Доказательство
Рассмотрим уравнение
Пусть получено некоторое решение общее однородного уравнения в виде
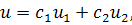
где – фундаментальная система решений.
Тогда для любого фиксированного можно определить функцию Коши, т.е. решение однородного уравнения вида
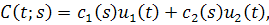
удовлетворяющее условию
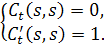
Иными словами,
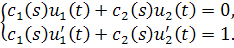
Полученная система является неоднородной системой относительно.
Определитель системы равен
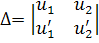
Этот определитель является определителем Вронского для системы, и так как он по условию равен 1, то можно применить правило Крамера для нахождения решения системы. В итоге получим
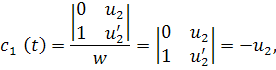
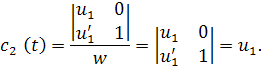
Подставим полученные данные в общее решение и получим
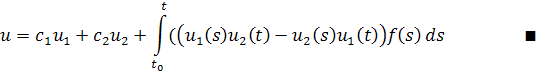
Пример 1.1 Рассмотрим уравнение, где .
Тогда линейно независимыми решениями , удовлетворяющие условию леммы (1.2), являются
,
.
Действительно, составив определитель Вронского, получим
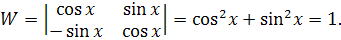
Таким образом, общее решение уравнения можно записать в виде
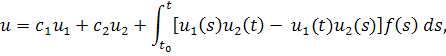
то есть
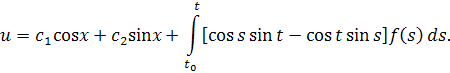
Рассмотрим уравнение . Тогдалинейно независимые решениями являются
,
.
Составив определитель Вронского получим, что
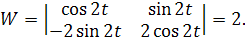
Таким образом, сделаем замену
,
.
Для таких функций определитель Вронского равен 1 и общее решение данного уравнения имеет вид
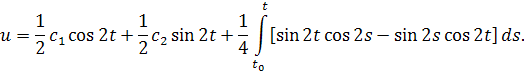
Лемма1.3. Пусть решение уравнения
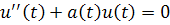
причем , то функция
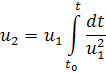
представляет собой другое, линейно независимое решение этого уравнения.
Доказательство
Этот результат получен при помощи стандартного метода вариации произвольных постоянных после подстановки
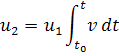
или на основании того, что для любых двух решений уравнения имеет место соотношение
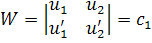
Это соотношение является уравнением первого порядка относительно функции , Решая это уравнение получим

Пример 1.2 Рассмотрим уравнение
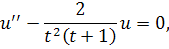
где .
Одним из решений данного уравнения является функция
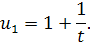
Возьмем , тогда выполняется условие .
Значит можно представить другое линейно независимое решение как
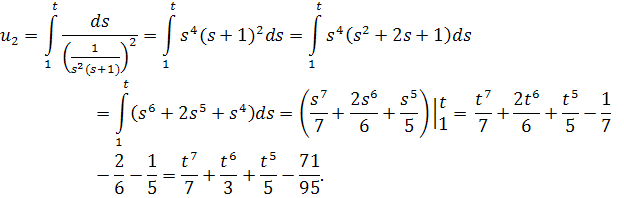
Таким образом, второе решение этого уравнения является
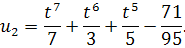
Далее в некоторых теоремах нам понадобится рассмотреть несобственный интеграл и его свойства.
Определение 1.4. Пусть . Если существует конечный предел
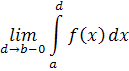
то функцияf называется интегрируемой в несобственном смысле на проме жутке, а указанный предел называется несобственным интегралом от функции f по промежутку .
Теорема 1.4. (Критерий Коши) Для сходимости интеграла
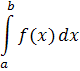
необходимо и достаточно, чтобы для любого существовало такое число , что для любых чисел таких, что,, выполнялось неравенство
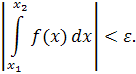
В одной из последующих теорем нам так же понадобится признаки сравнения функций при вычислении интегралов. Рассмотрим некоторые из них.
Признак 1.1. Пусть функции f(x) и g(x) определены на промежутке и удовлетворяют неравенству, тогда
- из сходимости интегралавытекаетсходимость интеграла .
- расходимость интегралавлечет расходимость
интеграла.
Признак 1.2. Если существует предел
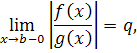
то
- при интегралы сходятся или расходятся одновременно
- при из сходимости интегралавытекает сходимость интеграла .
- прирасходимость интеграла влечет расходимость интеграла .
Пример 1.3Исследуем на сходимость интеграл
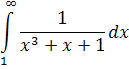
Рассмотрим функцию . Эта функция на бесконечности эквивалентна функции , поскольку выполняется условие
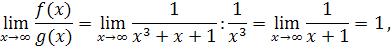
иными словами, .Значит сходимость интеграла 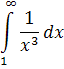
совпадает со сходимостью интеграла
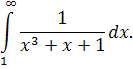
А такой интеграл легко вычислить
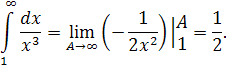
Значит, интеграл сходится, и исходный интеграл тоже сходится.
Глава 2
2.1 Случай .
В этом пункте мы перейдем к исследованию того, при каких
условиях все решения данного уравнения будут ограниченными при. Сначала рассмотрим уравнение
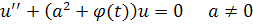
где является бесконечно малой при. Введем замену
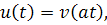
тогда и .
Подставляя данные в уравнение, получим
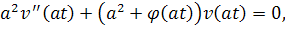
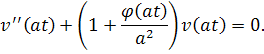
Выполняя заменыи , получим новое уравнение
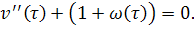
Таким образом, для удобства можно сразу рассматривать .
Возникает вопрос о связи решения данного уравнения с решения уравнения вида
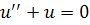
Покажемэту связь, но одного стремления недостаточно для того, чтобы гарантировать ограниченность всех решений данного уравнения.
Теорема 2.1.1 Все решения уравнения

ограничены, если выполняется условие
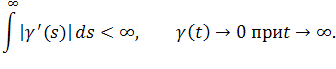
Доказательство
Покажем сначала, что все решения уравнения
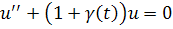
ограничены, если выполнено условие
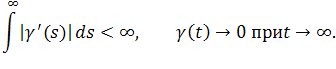
Умножим обе части на, тогда
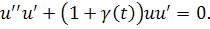
Далее, интегрируем и получаем
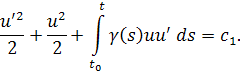
Интегрируя по частям, имеем
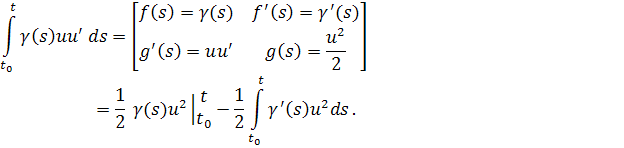
Отсюда,
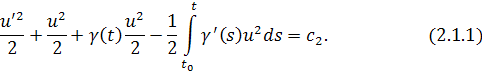
Так как , то
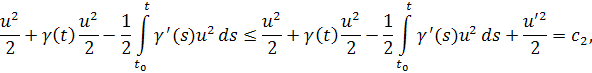
поэтому
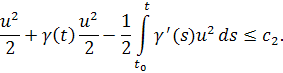
Возьмем настолько большим, чтобы при выполнялось неравенство. Это всегда можно сделать, так как при.Тогда для будем иметь
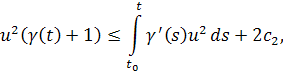
Откуда учитывая,
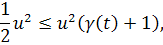
имеем
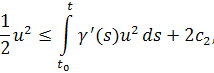
то есть
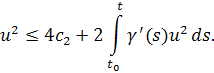
В итоге
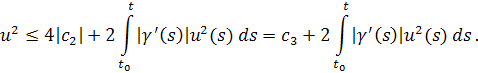
Так каки выполнено неравенство
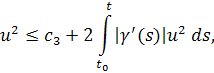
то,применяя лемму 1.1, получим, что для справедливо
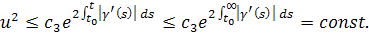
значит функция ограничена. А из формулы (2.1.1) следует, что и производ ная также ограничена.
Теорема 2.1.2 Если все решения уравнения
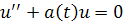
ограничены вместе со своими производным первого порядка, то и все реше ния
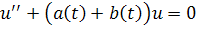
также ограничены вместе с их первыми производными, если только
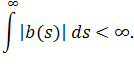
Доказательство
Рассмотрим уравнение
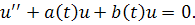
Предположим, чторешение такого уравнения, то есть
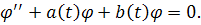
Рассмотрим уравнение
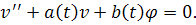
Заметим, чтотакже является решением этого уравнения. Тогда для него справедлива формула Коши
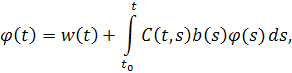
гдеэто решение однородного уравнения, а – функция Коши.
Оценим решение. Согласно условиям теоремы, решение однородного уравнения ограничено, значит , где –некоторая константа. Тогда
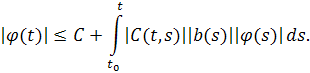
Так же в условии теоремы сказано, что решения ограничены вместе со своими первыми производными, то есть функцию Коши можно ограничить некоторой константой , тогдаполучим
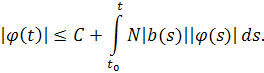
Поскольку выполнены условиялеммы Беллмана, а именно непрерывна на отрезке и , то каждое решение этого неравенства удовлетворяет оценке
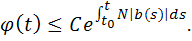
Так как
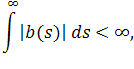
то
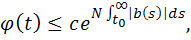
то есть каждое решение уравнения
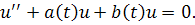
является ограниченным.
Теорема 2.1.3 Все решения уравнения
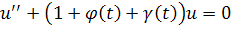
ограничены, если выполняются условия
(б)
Доказательство
Обозначим . Применяя теоремы 2.1.1 и 2.1.2, получаем, что все решения исходного уравнения ограничены.
Пример Рассмотрим уравнение
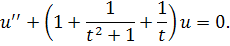
Функции удовлетворяют условиям, заданным в теореме, т.е.
,
.
Тогда решения такого уравнения являются ограниченными.
- Случай .
Определение 2.2.1Кусочно гладкойназывается функция, производная которой является непрерывно дифференцируемой.
Теорема 2.2.1 Если функция кусочно гладкая и монотонно стремится к , то все решения уравнения
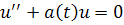
ограничены при .
Доказательство
Умножим обе части на. Имеем
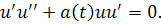
Интегрируяпо отрезку , получим
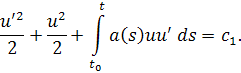
Поскольку
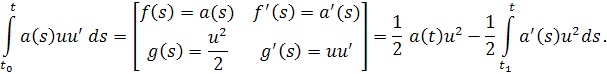
Имеем
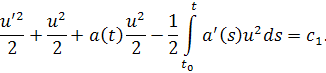
Оценивая снизу выражение, стоящее слева, получим
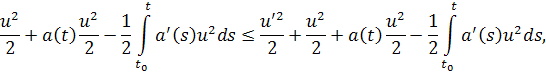
то есть
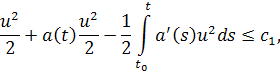
или
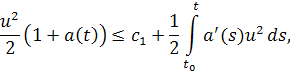
откуда
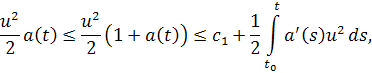
значит

Так как , то, не ограничивая общности, можно считать, что при . Следовательно,
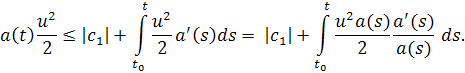
Все условия леммы 1.1 выполнены и так как значит
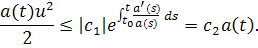
Следовательно,
ПримерРассмотримуравнение
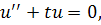
, непрерывно дифференцируемая.
Значит все решения уравнения ограничены при.
- Случай
Перейдем теперь к случаю, когда . Рассмотрение уравнения
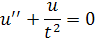
которое имеет два линейно независимых решения вида , где - корни уравнения , показывает, что решения уравнения этого типа могут быть неограниченными. Можно предположить, что если при функция стремится к нулю достаточно быстро, то решения уравнения стремятся к решениям уравнения .
Теорема 2.3.1 Рассмотрим уравнение
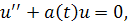
где
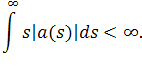
Тогда для любого его нетривиального решения и(t) существует и не могут одновременно равняться нулю.
Доказательство
Запишем уравнение в виде . Далее,
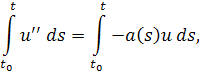
то есть
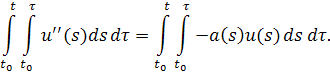
Или
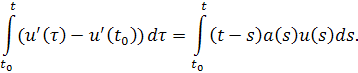
Обозначим , тогда
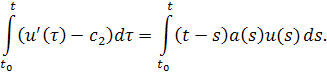
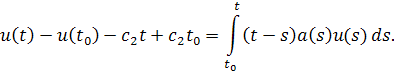
Выразими обозначим . В итоге имеем
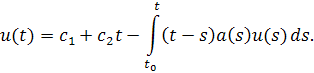
Отсюда, полагая получим
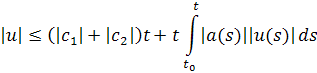
или
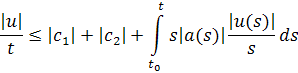
и, так как оба множителя больше нуля, применим лемму
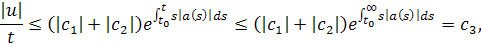
но из того, что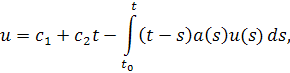
находим
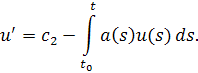
Таккак
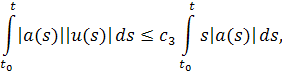
то интеграл сходится и имеет предел при. Обозначим
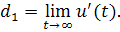
Если этот предел отличен от нуля, то , где при . Действительно, так как то для любого , найдется та кой номер, что начиная с этого номера будет выполнятся условие
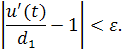
Пусть, например, , тогда отсюда следует, что
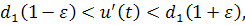
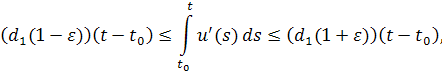
Домножим все части неравенства на
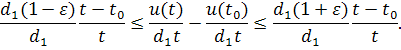
Поскольку при, то переходя в неравенстве к пределу, получим
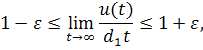
т.е. в силу произвольности
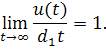
Если же , то первое неравенство имеет вид
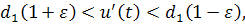
но домножив на , придем к тому же самому неравенству, что и при .
Теперь заметим, что в силу леммы 3 функция представляет со бой другое решение нашего уравнения, причем для него . В самом деле, если , то для имеем , откуда при
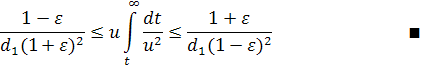
ПримерРассмотрим уравнение
,
где . Для него выполняется
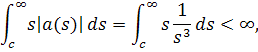
где – некоторая константа.
Тогда для любого нетривиального решения существует предел производной.
- Случай
Теорема 2.4.1 Пусть дано уравнение
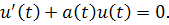
Eслипри , где , то уравнение обладает такой фундаментальной системой , что
,
при ,
при .
Доказательство
Рассмотрим более общее уравнение, содержащее параметр ,

которое обращается в (3.4) при .
Пустьопределено для . Будем искать решение уравнения (3.5) в виде ряда по степеням :
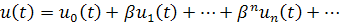
Сначала построим ряд для решения
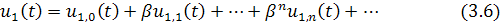
Положим и подставим разложение (3.6) в (3.5), приравняем коэффициенты при соответствующихстепенях .Тогда
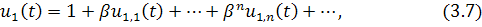
откуда
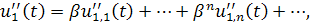
поэтому
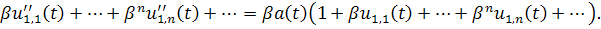
Таким образом, получаем рекуpрентные уравнения для определения коэффициентов разложения . Точнее говоря,
,
,
…
,
…
Функции последовательно находятся по формулам
;
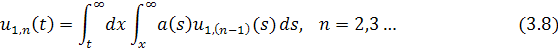
Докажем, что несобственные интегралы в формулах (3.8) сходятся, и оценим .
Из условия по определению следует, что существует такое , что при имеет место неравенство

Отсюдаполучаем
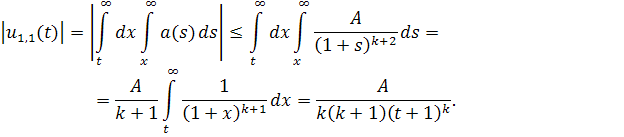
Аналогично

Предполагая, что для верно, покажем методом индукции, что для выполняется
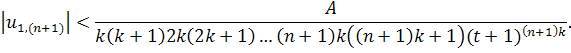
Темсамымочевидно, что
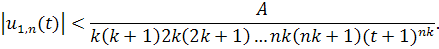
Используя полученные оценки, покажем, что ряд (3.6) сходится. Воспользуемся признаком Вейерштрасса. При
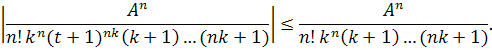
Ряд (3.6) мажорируется рядом
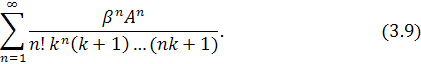
Исследуем полученный ряд на сходимость при помощи признака Даламбера. Итак,
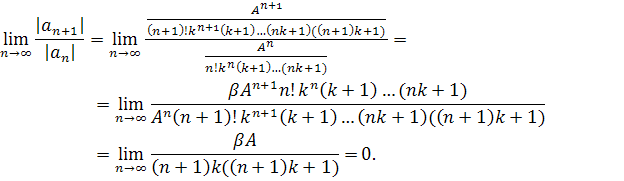
Ряд (3.9) сходятся, значит по теореме Вейерштрасса, ряд (3.6) сходится абсолютно и равномерно при , для любого и представляет решение уравнения (3.5).
Покажем, что . Рассмотрим
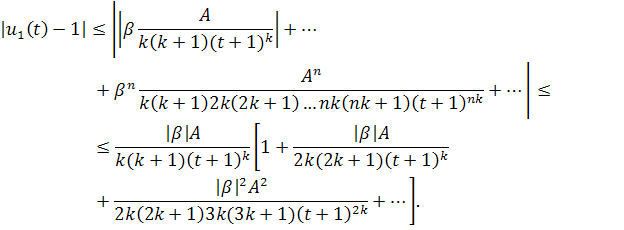
Теперь проверим на сходимость ряд, стоящий в квадратных скобках. Для начала воспользуемся признаком Вейерштрасса.
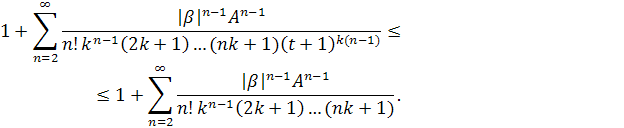
По признаку Даламбера
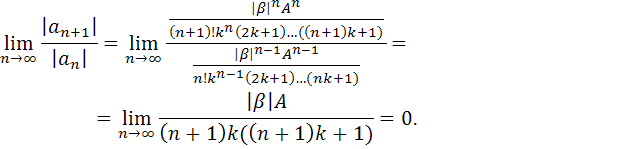
Значит ряд сходится, по признаку Вейерштрасса, ряд, стоящий в квадратных скобках сходится абсолютно и равномерно, и его сумма стремится к единице при . Отсюда имеем
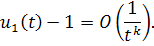
Для решения теорема доказана.
Будем искать решения в виде ряда
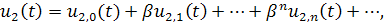
положим , то есть
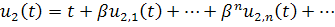
Тогда
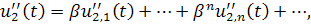
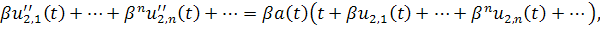
и получим уравнения для определения :
,
,
,
…
Пусть , тогда
,
,
Покажем, что несобственные интегралы сходятся. Действительно
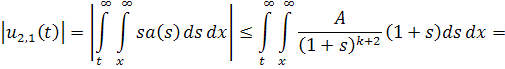
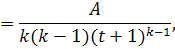
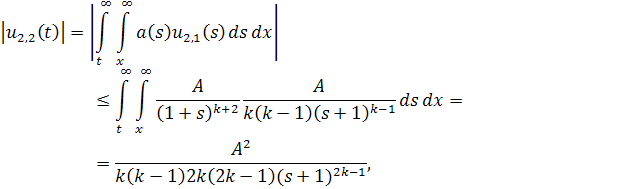
…
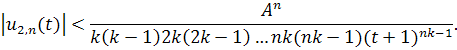
По признаку Вейерштрасса
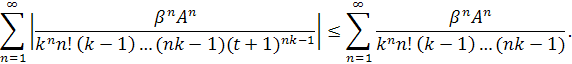
Полученный числовой ряд сходится. Действительно
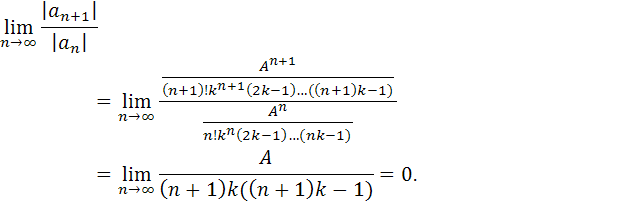
Значит, исходный ряд для сходится абсолютно и равномерно. Покажем, что
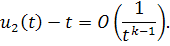
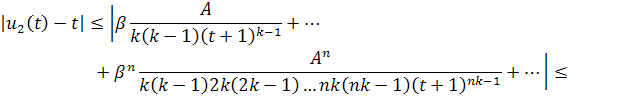
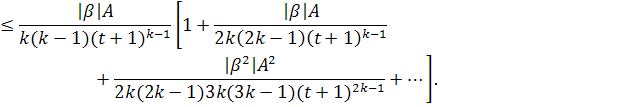
Проверим ряд в квадратных скобках на сходимость. По признаку Вейерштрасса имеем
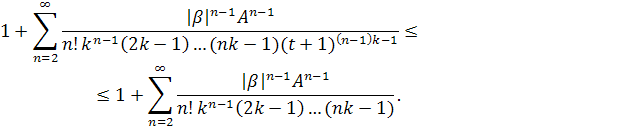
Воспользуемся признаком Даламбера
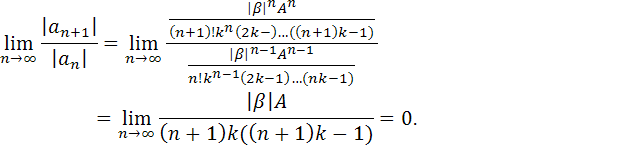
Значит, ряд сходится абсолютно и равномерно, отсюда имеем, что

Рассмотрим пример.
Пример 3.1.

Сделаем подстановку
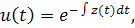
тогда
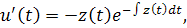
то есть
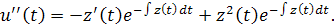
Подставим в уравнение
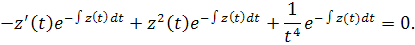
Теперь, умножив обе части уравнения на, получим
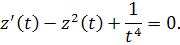
Сделаем замену , тогда
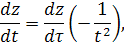
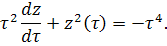
Теперь сделаем следующую замену и приведем полученное уравнение к уравнению с разделяющимися переменными
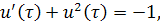
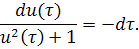
Проинтегрируем и получим
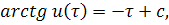
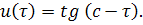
Теперь, используя замены и , получим решение уравнения относительно
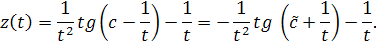
Вернемся к замене
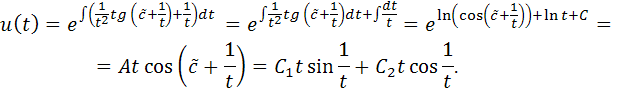
Получим фундаментальную систему решений
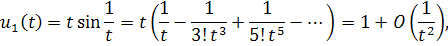
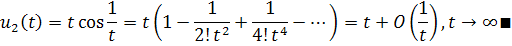
Глава 3
3.1 Уравнение ,
где .
Имеется обширный класс уравнений вида
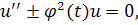
где, при .
Сейчас будет изложен метод, основанный на связи между уравнением
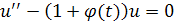
и уравнением Риккати
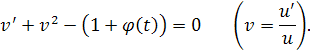
Полагая , получим для функции w уравнение
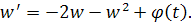
Уравнение имеет решение, стремящееся к нулю при. Оценим это решение через функцию . Имеем
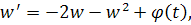
где свободный член, тогда
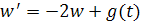
Это уравнение с разделяющимися переменными и его общее решение
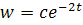
Можно найти для него функцию Коши, т.е. . Имеем
. Тогда решение имеет вид
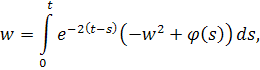
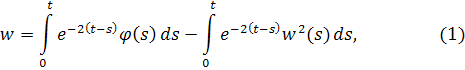
где для упрощения записи положим нижний предел равным нулю. Без ограничения общности можно считать, что. Применяя метод последовательных приближений, положим
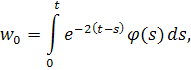
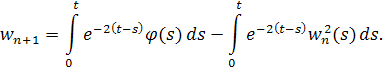
Используя оценку для функции получаем, что . Отсюда следует, что если , то и
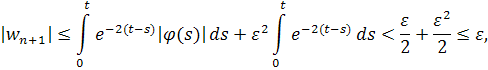
если . Значит, неравенство имеет место для всех n.
В итоге получаем
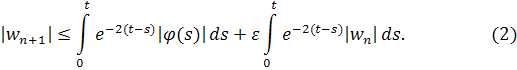
Покажем по индукции, что , если достаточно мало. Неравенство, очевидно, верно при n=0.
Подставим в оценку для и получим
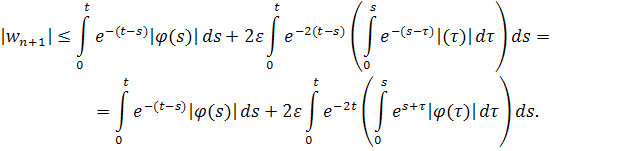
Оценим второе слагаемое полученной суммы:
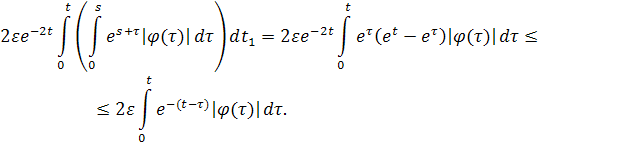
Пользуясь этой оценкой, находим, что
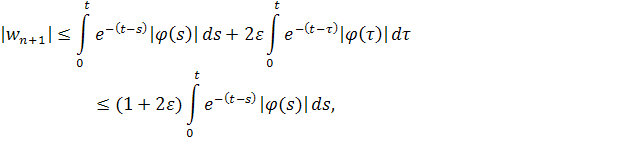
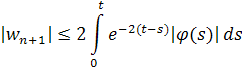
если .
Легко показать, что приближения сходятся к решению wинтегрального уравнения (1), удовлетворяющему неравенству
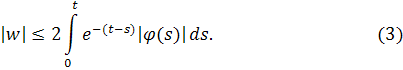
Так как
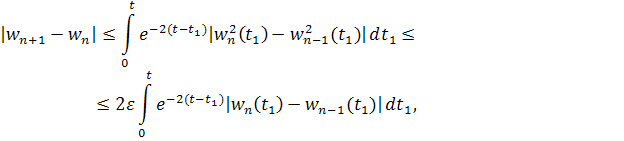
то переходя к , имеем
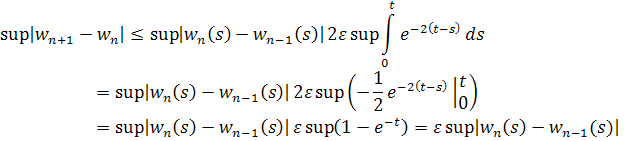
Значит, ряд
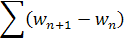
сходится равномерно при . Отметим для дальнейшего, что для доказательства существования решения уравнения (1) и для получения оценки (3) мы пользовались только тем, что .
Применяянеравенство Коши – Буняковского, получаем
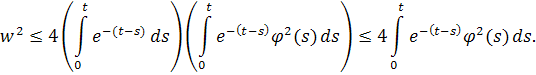
Возвращаясь к уравнению (1), получаем
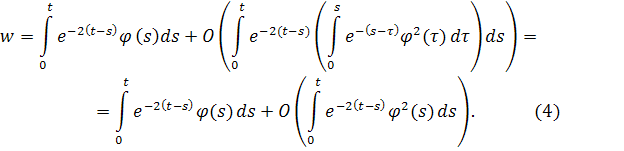
Так как , то поведение интеграла определяет асимптотическое поведение u. Применяя формулу (5),получаем
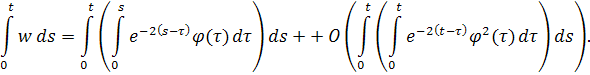
Меняем порядок интегрирования в обоих интегралах:
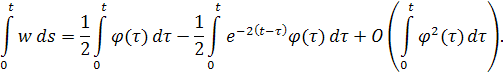
Так как при и , то мы видим, что
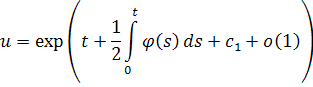
при .
Однако последний переход не совсем точен, так как величина O(1) не обязана иметь вид . Однако в данном случае под понимается
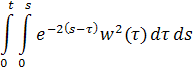
и из ограниченности этого интеграла следует стремление к его пределу при. Интеграл же
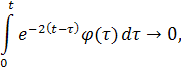
так как
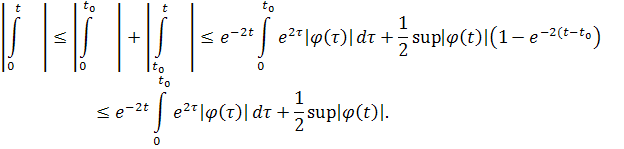
Асимптотическое поведение второго решения, линейно независимого с решением u, можно определить как обычно, применяя в качестве этого решения
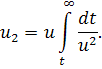
Иначе, можно рассмотреть уравнение, полученное из уравнения Риккати в результате подстановки
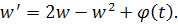
Соответствующее интегральное уравнение для решений, стремящееся к нулю, будет
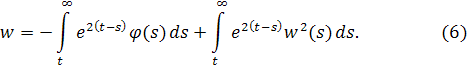
При этом все вкладки аналогичны проведенным выше. Отметим только, что необходимо пользоваться выражением
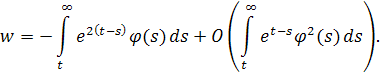
Сформулируем окончательный результат.
Теорема 1 Если функция удовлетворяет условиям:
- при ,
то уравнение обладает двумя решениями, имеющими соотвественно асимптотический вид:
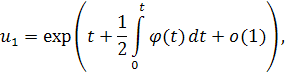
при .
3.2 Уравнение , где.
Метод, использованный в предыдущем пункте, применим для любого уравнение вида
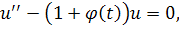
где при идля некоторого . Однако при этом чрезвычайно возрастают алгебраические затруднения. Ограничимся формулировкой результата при .
Теорема 3 Если функцияудовлетворяет условиям
- при
то существуют два решения уравнения

имеющие соответственно асимптотический вид:
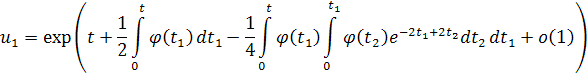
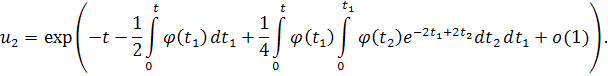
Доказательство
Предположим, что выполнено условие 1. Используем для доказательства метод, основанный на связи между уравнением
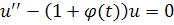
и уравнением Риккати
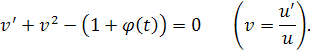
Полагая , получим для функции w уравнение
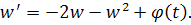
Уравнение имеет решение, стремящееся к нулю при. Оценим это решение через функцию . Имеем
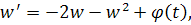
где свободный член, тогда
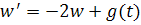
Это уравнение с разделяющимися переменными и его общее решение
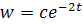
Можно найти для него функцию Коши, т.е. . Имеем
. Тогда решение имеет вид
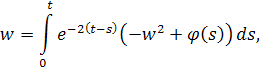
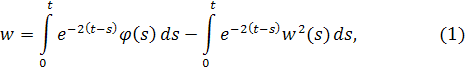
где для упрощения записи положим нижний предел равным нулю. Без ограничения общности можно считать, что. Применяя метод последовательных приближений, положим
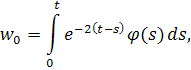
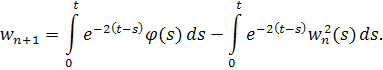
Используя оценку для функции получаем, что . Отсюда следует, что если , то и
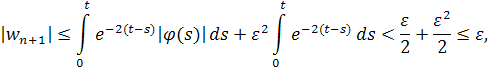
если . Значит, неравенство имеет место для всех n.
В итоге получаем
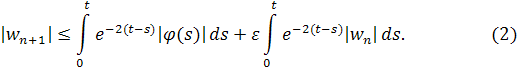
Покажем по индукции, что , если достаточно мало. Неравенство, очевидно, верно при n=0.
Подставим в оценку для и получим
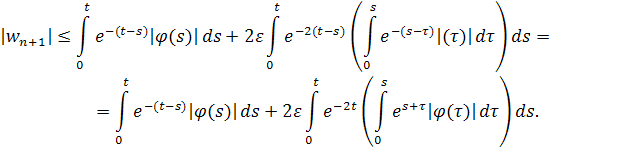
Оценим второе слагаемое полученной суммы:
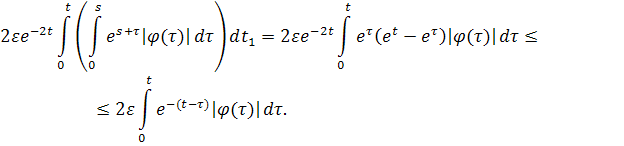
Пользуясь этой оценкой, находим, что
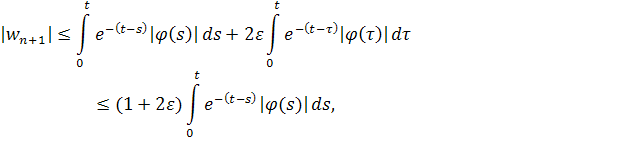
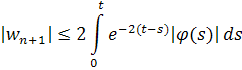
если .
Легко показать, что приближения сходятся к решению wинтегрального уравнения (1), удовлетворяющему неравенству
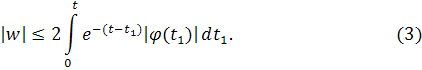
Так как
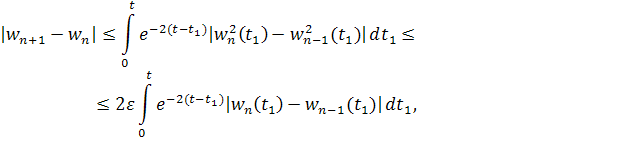
то переходя к , имеем
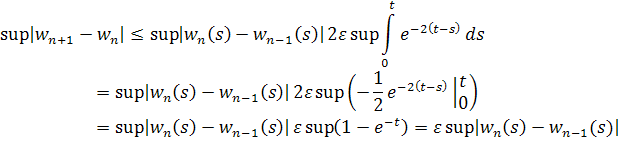
Значит, ряд
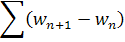
сходится равномерно при .
Применим неравенство Гельдераи получим
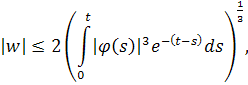
из которого видно, что .
Возьмем уже известное равенство
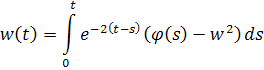
и проинтегрируем его.
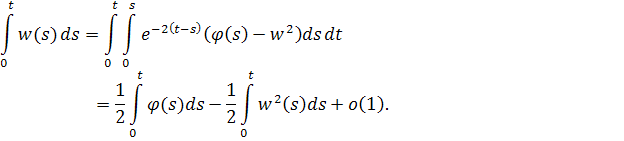
Однако попробуем возвести в квадрат это выражение
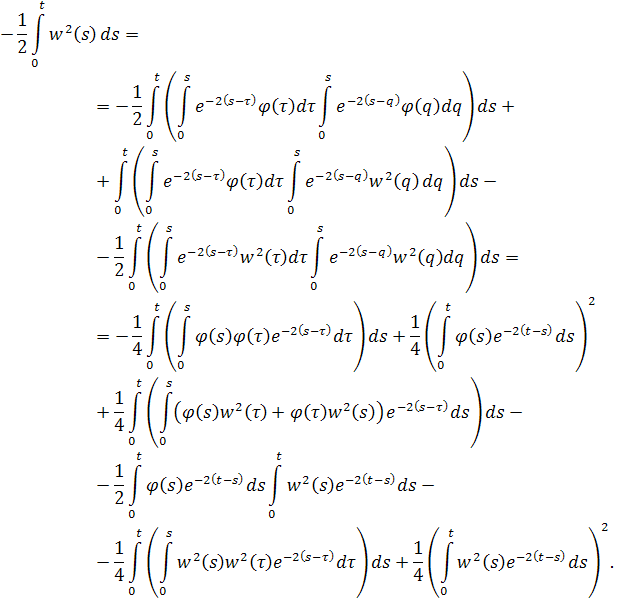
Как уже рассматривалось ранее, видно, что
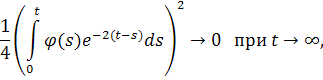
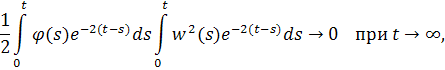
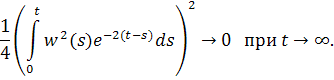
Покажем, что третий интеграл ограничен
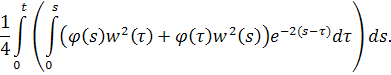
Воспользуемся неравенством

и оценим интеграл.
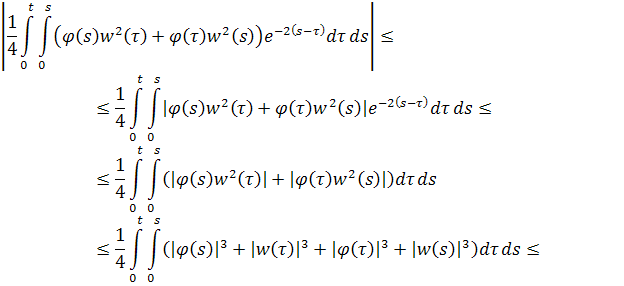
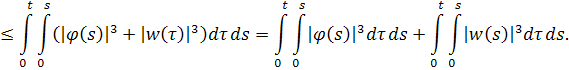
Очевидно, что интегралы сходятся, а значит исходный интеграл ограничен.
Необходимо так же показать, что пятый интеграл в сумме имеет конечный предел.
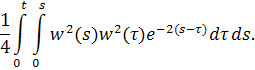
Оценим интеграл, предварительно воспользовавшись неравенством
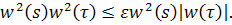
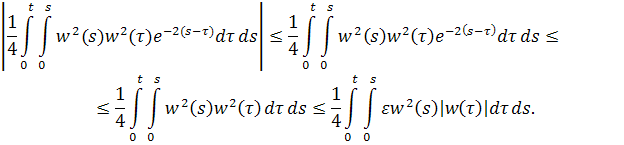
Получаем, что интеграл имеет конечный предел при.
В итоге интеграл принимает следующий вид
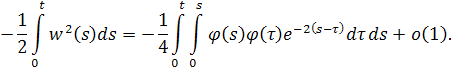
Возвращаемся к решению уравнения
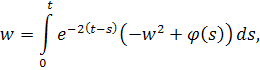
и получаем
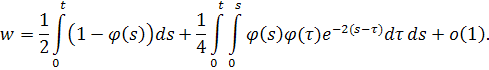
Необходимо вспомнить, что вначале была сделана замена , где . Возвратимся к исходной переменной
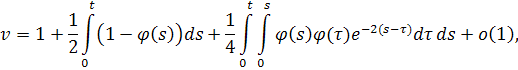
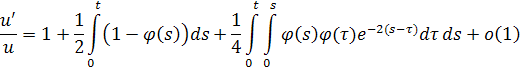
Интегрируя и потенцируя, получаем асимптотический вид решения исходного дифференциального уравнения
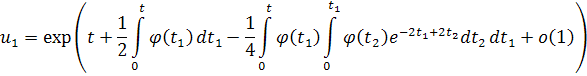
Асимптотическое поведение второго решения, линейно независимого с решением u, можно определить как обычно, применяя в качестве этого решения
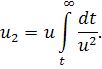
Иначе, можно рассмотреть уравнение, полученное из уравнения Риккати в результате подстановки
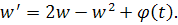
Соответствующее интегральное уравнение для решений, стремящееся к нулю, будет
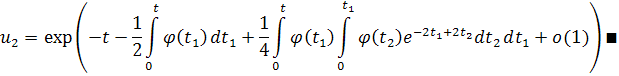
Метод, использованный в предыдущих теоремах, применим для любого уравнения вида
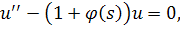
где идля некоторого .
Теорема. Пусть дано уравнение
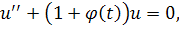
где Тогда если
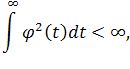
тогда существует два комплексных решения, имеющие вид
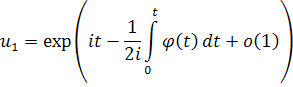
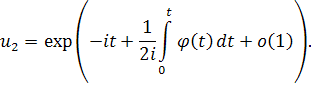
Доказательство
Мы будем пользоваться методом, основанным на связи между уравнением
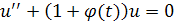
и уравнением Риккати
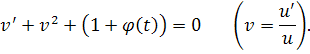
Полагая , получим для функции w уравнение
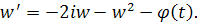
Уравнение имеет решение, стремящееся к нулю при. Оценим это решение через функцию . Имеем
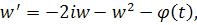
где свободный член, тогда
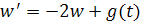
Это уравнение с разделяющимися переменными и его общее решение
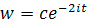
Можно найти для него функцию Коши, т.е. . Имеем
. Тогда решение имеет вид
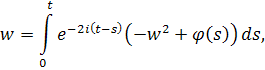
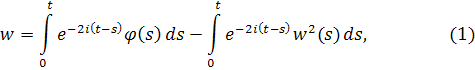
где для упрощения записи положим нижний предел равным нулю. Без ограничения общности можно считать, что. Применяя метод последовательных приближений, положим
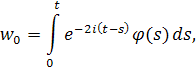
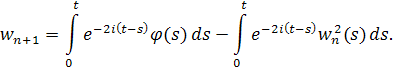
Используя оценку для функции получаем, что . Отсюда следует, что если , то и
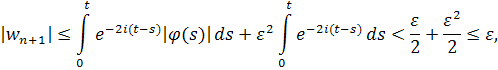
если . Значит, неравенство имеет место для всех n.
В итоге получаем
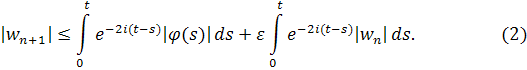
Покажем по индукции, что , если достаточно мало. Неравенство, очевидно, верно при n=0.
Подставим в оценку для и получим
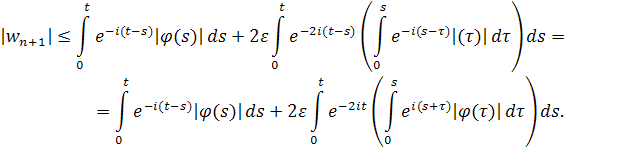
Оценим второе слагаемое полученной суммы:
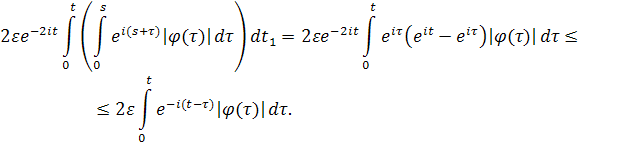
Пользуясь этой оценкой, находим, что
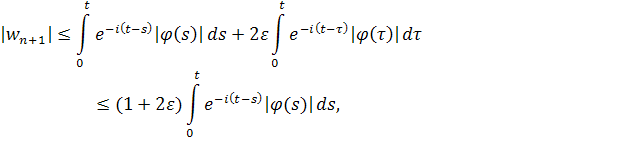
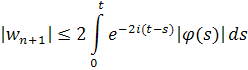
если .
Легко показать, что приближения сходятся к решению wинтегрального уравнения (1), удовлетворяющему неравенству
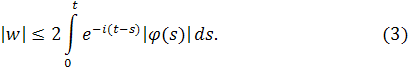
Так как
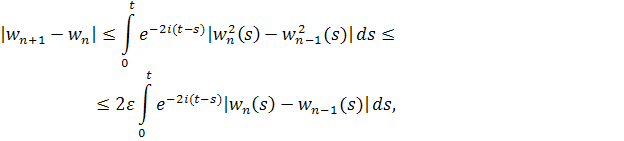
то переходя к , имеем
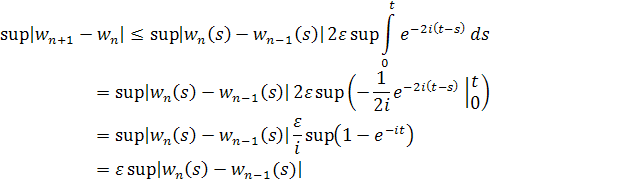
Значит, ряд
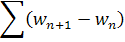
сходится равномерно при . Отметим для дальнейшего, что для доказательства существования решения уравнения (1) и для получения оценки (3) мы пользовались только тем, что .
Применяянеравенство Коши – Буняковского, получаем
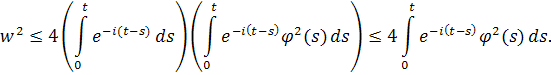
Возвращаясь к уравнению (1), получаем
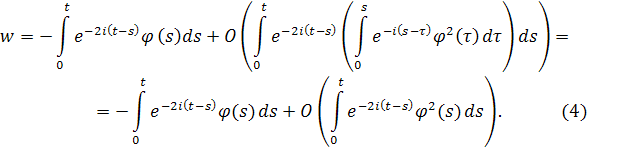
Так как , то поведение интеграла определяет асимптотическое поведение u. Применяя формулу (5),получаем
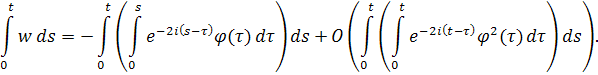
Меняем порядок интегрирования в обоих интегралах:
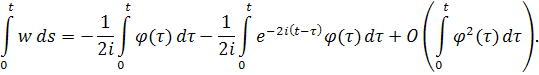
Так как при и , то мы видим, что
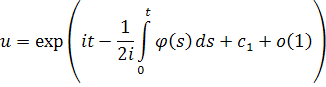
при .
Однако последний переход не совсем точен, так как величина O(1) не обязана иметь вид . Однако в данном случае под понимается
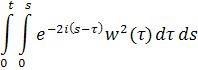
и из ограниченности этого интеграла следует стремление к его пределу при. Интеграл же
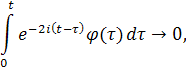
так как
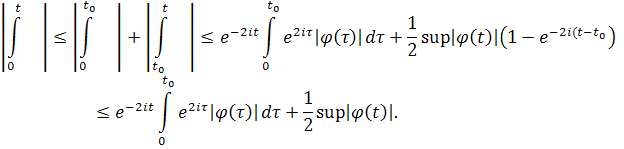
Асимптотическое поведение второго решения, линейно независимого с решением u, можно определить как обычно, применяя в качестве этого решения
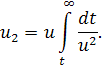
Иначе, можно рассмотреть уравнение, полученное из уравнения Риккати в результате подстановки
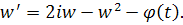
Соответствующее интегральное уравнение для решений, стремящееся к нулю, будет
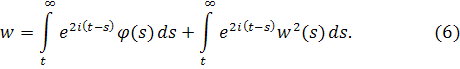
При этом все вкладки аналогичны проведенным выше. Отметим только, что необходимо пользоваться выражением
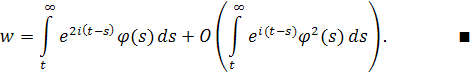
Асимптотика решения дифференциального уравнения в окрестности бесконечно удаленной точки