Наблюдаемость технических состояний и видов технического состояния

Лекция 3

1. Теоретико-множественная интерпретация видов технического состояния на множестве наблюдаемых состояний

2. Понятие полной наблюдаемости технических состояний и видов технического состояния

3. Глубина контроля и диагностирования

Непосредственное измерение значений переменных состояния

xk,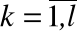

невозможно. Измерить сопротивление запирающего слоя в полупроводниковом элементе, с учётом его схемной связи с другими элементами, в условиях эксплуатации практически невозможно. Кроме того физическая природа переменных, определяющих внутренние свойства объектов, не всегда бывает известной.

Поэтому для оценки переменных состояния необходимо использовать косвенные признаки - выходные параметры, имеющие с переменными состояния тесную корреляционную взаимосвязь. В отличие от переменных xk выходные параметры можно наблюдать и измерять, поскольку это вполне конкретные физические величины –токи, напряжения, температуры, давления, амплитуды виброперемещений и т.д. В силу перечисленных особенностей выходные параметры принимаются в качестве контролируемых признаков (КП).

Значения выходных параметров, измеренных на объекте в заданный момент времени, образуют вектор

Y<n>= (y1, y2,…, yn)т. (1)

Вектор Y<n> называется наблюдаемым состоянием объекта; координаты yj, 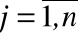- контролируемые признаки.

Множество КП должно быть достаточным, чтобы фиксировать все значимые изменения переменных состояния объекта.

КП регистрируются на выходах, которые принято называть контрольными точками объекта.

Множество наблюдаемых состояний

Y = {Y<n>},

также как и множество

Х = {X<l>}

может быть разбито на подмножества, соответствующие различным видам технического состояния объекта. Причём имеет место взаимно однозначное соответствие между подмножествами

Хр Yр,

Х\Хр Y\Yр, (2)

Хпф(t) Yпф(t),

Х\Хпф(t) Y\Yпф(t).

Подмножество наблюдаемых состояний Y\Yр также как и Х\Хр может быть подвергнуто разбиению на подмножества, соответствующие отказам различных составных частей объекта. При таком более детальном разбиении взаимно однозначное соответствие сохраняется:

(Х\Хр)i (Y\Yр)i, 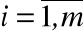. (3)

Аналогично при контроле правильности функционирования

(Хпф(t))k (Yпф(t))k, .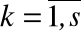

В силу взаимной однозначности подмножества Yр, Yпф(t), Y\Yр, Y\Yпф(t), (Y\Yр)i, (Yпф(t))k также называют видами технического состояния.

Исходя из вышеизложенного, представляется естественным трактовку отказов объекта на множестве Y производить так же, как и на множестве X.

Под отказом понимается событие, состоящее в переходе текущего состояния объекта:

из подмножества Yр в подмножество Y\Yр (контроль работоспособности);

из подмножества Yпф(t)) в подмножество Y\Yпф(t)) (контроль правильности функционирования).

На объект имеют место и входные воздействия. Эти воздействия можно представить вектором переменных

U<h>= (u1, u2,…, uh)т. (4)

Структурную схему объекта можно представить следующим образом:

Рис.1. Структурная схема объекта

Входные воздействия на объект могут быть двух видов:

) Входные воздействия поступают от средств К и Д и являются специально организованными воздействиями. Такие воздействия называются тестовыми. Их можно изменять в зависимости от специфики решаемых задач. К и Д при тестовых воздействиях называются тестовыми.

) Входные воздействия являются внешними по отношению к системе К и Д, определяются они как рабочим алгоритмом функционирования объекта, так и внешней средой. Такие воздействия называются рабочими, а К и Д –функциональными (рабочими).

Очевидно также, что переменные

up, ,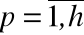

xk, ,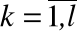

yj, .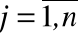

изменяются во времени.

Пусть в какой-либо форме установлены функциональные зависимости

yj = j(x1, x2,…, xl, u1, u2,…,uh, t), 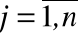(5)

или в векторном виде

Y<n>= Ф(X<l> , U<h>, t ), (6)

где t –момент времени, в который производится наблюдение объекта, tT, T- множество моментов времени, в которые наблюдается объект.

Если функция Ф имеет обратную функцию Ф-1, то для каждого фиксированного момента времени t0 и фиксированного входного воздействия U<h>0 можно найти состояние объекта при любом наблюдаемом состоянии Y<n>:

X<l> = Ф-1(Y<n>, U<h>0, t0). (7)

Существование обратной функции (7) указывает на то, что отображение

Ф: U X T Y (8)

является инъективным (вложением), где

U X T = {( U<h>, X<l>, t)}.

Инъективным называется отображение, если каждый элемент множества-образа имеет в качестве прообраза не более чем один элемент.

Пример инъективного отображения из числа общеизвестных функций. Рассмотрим

Ф: X Y,

где

X = R, Y = R (R –множество вещественных чисел).

Если Ф(x) = еxpt, то Ф –инъективно. По одному прообразу имеют только положительные элементы множества Y (т.е. элементы множества R+); отрицательные элементы множества Y прообразов не имеют.

Пусть

Ф: U X T Y,

где

Ф(x,u,t) = lnxtguеxpt,

U = (–/2; /2), X = R+, , T = R, Y = R, xX , uU, tR.

Утверждать, что отображение Ф будет инъективным в последнем случае нельзя.

В теории систем и управления отображение (8) называется оператором выхода. Если данный оператор обладает свойством инъективности, объект называется полностью наблюдаемым.

Полная наблюдаемость означает возможность идентификации любого технического состояния (см.(7)):

X<l> Y<n>.

О полной наблюдаемости можно рассуждать только лишь теоретически. В реальных условиях ее обеспечить невозможно и в этом нет практической необходимости. Например, при диагностировании это означает определить отказ на уровне элементарной составной части (резистора, транзистора). Чтобы обеспечить полную наблюдаемость может потребоваться неограниченно большое число контрольных точек.

При разработке объекта предусматривается некоторое ограниченное количество этих точек. Поэтому текущее техническое состояние можно идентифицировать только с некоторым подмножеством, соответствующим тому или иному виду технического состояния. Например, поиск отказов осуществляется с точностью до функциональных элементов (ФЭ) определенного уровня (сменных модулей):

Y<n> (Y\Yр)i, .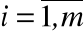

Отказы внутри этих элементов являются неразличимыми на множестве имеющихся КП. Следовательно, текущее ТС идентифицируется с подмножеством ТС, соответствующим отказу какого-то ФЭ.

Аналогичная ситуация имеет место и при контроле правильности функционирования. В процессе проверки выполнения команд и отработки режимов работы объекта нет практической необходимости в определении каждого состояния. В рамках одного и того же режима между состояниями целесообразно не делать каких-либо различий:

Y<n> (Yпф(t))k, .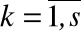

Только в этом случае задача определения технического состояния становится обозримой и практически разрешимой.

Глубина контроля и диагностирования определяется соотношением мощности всего множества технических состояний объекта и мощности множеств, охватываемых отдельными видами технического состояния.

Глубина диагностирования определяется соотношением мощности всего множества неработоспособных состояний объекта Y\Yр и мощности множеств (Y\Yр)f, соответствующих отказам отдельных ФЭ.

Пусть задано два варианта разбиения множества Y\Yр:

1) (Y\Yр)i , ;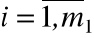

2) (Y\Yр)i , .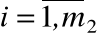

Если m1 < m2, то вторым вариантом задается большая глубина диагностирования.

Теоретически можно задать целый ряд вариантов разбиения

m1 < m2 <…< mn.

При увеличении n глубина диагностирования увеличивается, а мощность множеств (Y\Yр)i уменьшается.

Физическая интерпретация понятия глубины диагностирования

На множестве Y\Yр выделяется 7 подмножеств: m =7.

В общем случае любой ФЭ имеет свою структуру, например, ФЭ-4.

Глубина контроля правильности функционирования определяется степенью дискретизации всего алгоритма функционирования объекта на отдельные режимы функционирования.

Пусть задано два варианта разбиения множества Yпф(t):

1) (Yпф(t))k, ;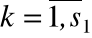

2) (Yпф(t))k, .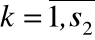

Если s1 < s2, то вторым вариантом задается большая глубина контроля правильности функционирования.

Теоретически можно задать целый ряд вариантов разбиения

s1 < s2 <…< sn.

При увеличении n глубина контроля правильности функционирования увеличивается, а мощность множеств (Yпф(t))k уменьшается.

В силу (2) и (3) все изложенные рассуждения можно провести на множестве X.

Понятия глубины контроля работоспособности не существует.

Наблюдаемость технических состояний и видов технического состояния