УСТАЛЕНИЙ РЕЖИМ. НЕРІВНОМІРНІСТЬ РУХУ МЕХАНІЗМУ
Лекція 19
1. УСТАЛЕНИЙ РЕЖИМ. НЕРІВНОМІРНІСТЬ РУХУ
МЕХАНІЗМУ
Для механізмів з одним ступенем вільності усталеним рухом називається такий, за якого швидкість початкової ланки (узагальнена швидкість) є періодичною функцією часу. Графік (t) при сталому русі представлений на рис. 5.
Як видно, кутова швидкість періодично коливається відносно деякого постійного середнього значення.
Період зміни швидкості початкової ланки (узагальненої швидкості механізму) називається циклом сталого руху або скорочено циклом. Час циклу дорівнює чи кратний періоду дії сил. Тому при сталому режимі сума робіт усіх сил за цикл дорівнює нулю:
. (14)
Через те, що робота сил ваги за цикл дорівнює нулю, то рівність (14) буде виконуватися, якщо робота рушійних сил за цикл дорівнює роботі всіх сил опору за цикл (за модулем)
. (15)
Рівняння робіт є основним енергетичним рівнянням усталеного режиму. З нього випливає, що збільшення кінетичної енергії механізму за цикл не відбувається і, отже, кутова швидкість початкової ланки на початку і в кінці циклу однакова.
Отже, при сталому режимі швидкість початкової ланки хоча і залишається в середньому постійною, але усередині циклу змінюється, проходячи через максимальне max i мінімальне min значення (рис.5.). Нерівномірність обертання оцінюється коефіцієнтом нерівномірності
, (16)
де ср – середня за цикл швидкість.
З рівняння (16) видно, що - характеризує розмах коливань швидкості відносно її середнього значення. Чим меншим буде коефіцієнт , тим відносно меншим є розмах коливань, тим спокійніше обертається початкова ланка. Величина ср підраховується за формулою
, (17)
у якій n - частота обертання початкової ланки.
Для кожного виду машин є своя припустима величина коефіцієнта нерівномірності , вироблена практикою. Так для металорізальних верстатів це , для прядильних машин , для дизельного привода електрогенераторів .
Коефіцієнт нерівномірності є величина дуже мала, що дозволяє прийняти середню величину кутової швидкості рівною середньому арифметичному з її максимального і мінімального значень.
. (18)
Спільний розв’язок рівнянь (17) і (18) дає величину максимальної і мінімальної швидкості:
; (19)
. (20)
Як видно з рівнянь відмінність max i min від ср віднесене до ср складає ,тобто не більше 2%.
В усталеному режимі працюють дуже багато машин (верстати, преси, прокатні стани, лісопильні рами, текстильні машини, генератори електричної енергії, компресори, насоси і т.д.). Найкраща умова для роботи всіх цих машин - абсолютно рівномірне обертання їхнього головного вала (прийнятого звичайно в якості початкової ланки).
Щоб одержати обертання головного вала машини з циклічною нерівномірністю, не перевищуючої необхідної величини, на головному валу машини закріплюють додаткову масу, виконану у виді колеса з розвитим ободом і названу маховиком.
Отже, основне призначення маховика складається в обмеженні коливань кутової швидкості в межах, установлених величиною коефіцієнта нерівномірності. Визначення моменту інерції маховика за заданими умовах руху здійснюється в процесі проектування машини і складає одну з задач її динамічного синтезу.
2. ВИЗНАЧЕННЯ МОМЕНТА ІНЕРЦІЇ МАХОВИКА МЕТОДОМ ВІТТЕНБАУЕРА.
Метод базується на залежності кінетичної енергії для ланки зведення
, (1)
де, - зведений момент інерції механізму;
- кутова швидкість ланки зведення механізму (машини).
Залежність (1) можна записати у вигляді:
(2)
Отже, значення можна визначити , знаючи відношення кінетичної енергії до зведеного моменту інерції для кожного положення механізму, тобто потрібно мати залежність
Тзв=Тзв(Ізв),
виключивши спільний параметр .
Діаграму Тзв=Тзв(Ізв) називають кривою Віттенбауера.
Маючи діаграму Віттенбауера, можна визначити кутову швидкість ланки зведення у будь-якому положенні механізму.
На рис. 1. зображена діаграма Тзв=Тзв(Ізв), яка для одного циклу усталеного руху буде замкненою кривою, оскільки зміна кінетичної енергії за один цикл дорівнює нулю.
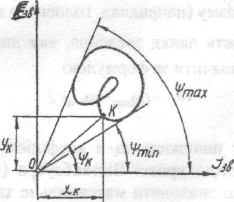
Рис.1.
У будь-якому положенні механізму, яка визначається точкою к , кутова швидкість ланки зведення
,
де,
тоді ,
Отже кутова швидкість у точці k визначається тангенсом кута, який з'єднує цю точку на діаграмі з початком координат. Так можна визначити у будь-якому положенні механізму.
Методику знаходження моменту інерції маховика методом Віттенбауера розглянемо на прикладі механізму плунжерного насоса.
Вважаємо заданими величинами n1 , коефіцієнт нерівномірності ходу d, та діаграма сил тиску на поршень p=p(s) , де s- переміщення поршня насоса. Зведений момент рушійних сил вважаємо сталим (Мр=const)
Порядок розв'язування задачі наступний:
- Будуємо п положень механізму (на рис. 1.29, а побудовано 12 положень
механізму) і плани швидкостей для цих положень (рис. 1.29, в).
- Користуючись планами механізмів (рис. 1.29, а) та діаграмою сил тиску
p=p(s) (рис 1.29, б), визначаємо величину сили опору fo, для простоти
нехтуючи всіма іншими силами опору,
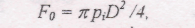
де D - діаметр поршня насоса, р, - тиск повітря на поршень, який визначається відповідною ординатою у. на діаграмі з врахуванням масштабу р.р :
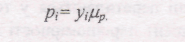
3. Користуючись залежностями (1.43)...(1.45), знаходимо значення зведеного моменту сил опору, прийнявши кривошип ОА ланкою зведення. У нашому випадку
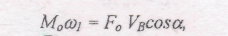
де а - кут між напрямком сили F д і швидкістю точки В (а. = 0 або 180°). Тоді
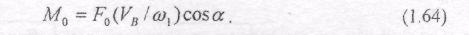
На основі одержаних значень А/в, вибравши масштаби мц і м^, будуємо діаграму зведених моментів сил опору мп= М0 (ц) як функцію кута ц повороту кривошипа (рис. 1.29, г).
4. Графічним інтегруванням діаграми М0 = М0 (ц) будуємо діаграму робіт
сил опору А о = ао (ц) (рис. 1.29, д). Масштаб роботи знаходимо за формулою
вБ= мц мпЗ, де З - полюсна відстань.
5. Оскільки зведений момент рушійних сил Мр прийнято сталим, то його
робота пропорційна куту поворота ц ( Ар= Мр ц). З другого боку, його робота за
період усталеного руху повинна чисельно дорівнювати сумі робіт опору, яка
зображена на рис. 1.29, д відрізком ВС тому, з'єднавши точку О з точкою С
прямою, одержимо діаграму Ар= Мр (ц).
6. Графічним диференціюванням діаграми Ар= Мс(ц) будуємо діаграму
зведених моментів рушійних сил Мс=М(ц). Для цього досить провести з
полюса С промінь РК (рис. 1.29, г), паралельний лінії ОС, до перетину з віссю
ординат М і через точку К провести лінію, паралельну осі ц .
I. Будуємо діаграму зміни (перепаду) кінетичної енергії механізму без
маховика ДЕ=ўЕ(ц), враховуючи, що ДЕ= Ар - А0 (рис. 1.29, е). Тобто
відкладаємо різницю ординат діаграм робіт вверх або вниз від осі абсцис у
залежності від знаку ДЕ .
8. Користуючись залежностями (1.46)...(1.49), знаходимо значення зведе�
ного момента інерції механізму (без маховика) і будуємо діаграму
(без маховика) і будуємо діаграму
9. На підставі двох діаграм AE=AE(AJM) і Д1,в =Д],,(ц), виключивши
спільний член ц, будуємо діаграму ДЕ=ДЕ(М3в) (рис. 1.29, ж).
10. Підраховуємо кути ШзЯбч і fmin, які визначають на діаграмі Е-,, =„ (J3e)
найбільші і найменші значення кутової швидкості ланки зведення (5.63), за
формулами:
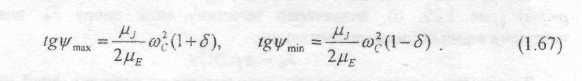
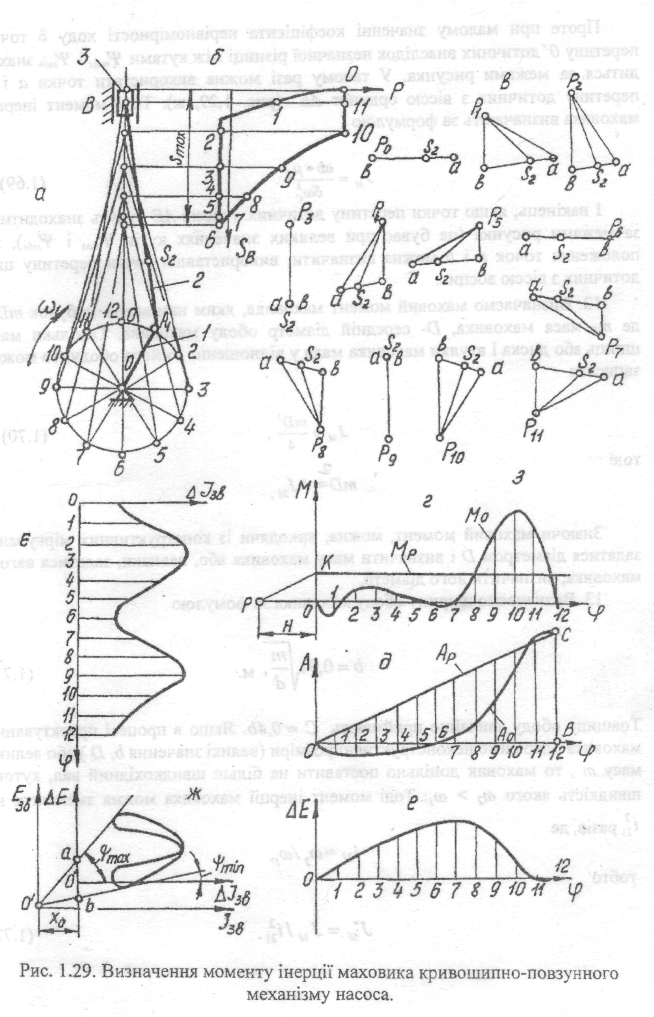
I1. Проводимо дотичні до кривої ДЕ=ДЕ(Д]єв) відповідно під кутами ШзМЧ
іУ„,ш до осі 4/„. Ці дотичні перетинаються у точці О'. Отже, для того, щоб
забезпечити заданий коефіцієнт нерівномірності ходу д , необхідно розмістити
початок координат діаграми Е„=ЕМ (Jla) у точці ()'. Тоді відрізок Х0 визначає у
масштабі мй момент інерції маховика, тобто

Проте при малому значенні коефіцієнта нерівномірності ходу 5 точка перетину 0 дотичних внаслідок незначної різниці між кутами fmM і Утіп знаходиться за межами рисунка. У такому разі можна використати точки а і b перетину дотичних з віссю ординат АЕ (рис, 1,29, ж). Тоді момент інерції маховика визначають за формулою

І накінець, якщо точки перетину дотичних з віссю АЕ будуть знаходитися за межами рисунка (це буває при великих значеннях кутів f^. і Ут!„), то положення точок а і Ь можна визначити, використавши точки перетину цих дотичних з віссю абсцис.
12. Визначаємо маховий момент маховика, яким називають добуток mD2,
де т- маса маховика, D- середній діаметр ободу маховика. Оскільки маса
шпиць або диска і втулки маховика мала у відношенні до його ободу, то можна
записати
тоді  ч
ч
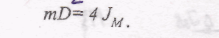 ' -
' -
Знаючи маховий момент, можна, виходячи із конструктивних міркувань, задатися діаметром D і визначити масу маховика або, навпаки, задатися вагою маховика, визначити його діаметр.
13. Визначаємо ширину ободу маховика за фомулою

Товщину ободу звичайно приймають С » 0,4Ь. Якщо в процесі проектування маховика одержимо неконструктивні розміри (великі значення b, D ) або велику масу т , то маховик доцільно поставити на більш швидкохідний вал, кутова швидкість якого а>2 > (Oj. Тоді момент інерції маховика можна зменшити на І2\ разів, де
тобто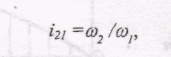

PAGE 7
УСТАЛЕНИЙ РЕЖИМ. НЕРІВНОМІРНІСТЬ РУХУ МЕХАНІЗМУ