ТЕОРЕМА ЖУКОВСЬКОГО

Лекція 15

ТЕОРЕМА ЖУКОВСЬКОГО

Теорема: Якщо силу, прикладену до якої-небудь точки ланки плоского механізму перенести паралельно самій собі в однойменну точку поверненого на 90 градусів плану швидкостей, то момент цієї сили відносно полюса плану швидкостей буде пропорційний її потужності.

Повернений на 90 градусів план швидкостей називають жорстким важелем Жуковського.

Доведення: На рис. 1, а покажемо ланку ВС, що здійснює плоскопаралельний рух. Відомі вектори швидкостей точок В і С. Нехай у точці S ланки прикладена деяка сила F.

Швидкість точки S визначимо з побудованого плану швидкостей (рис.1,б). Кут між вектором сили F і вектором швидкості позначимо .

Повернемо план швидкостей на 90 градусів (рис.2) у довільному напрямку й у точку s перенесемо вектор сили . З полюса поверненого плану швидкостей опустимо на лінію дії сили перпендикуляр до перетину в точці k .

Розглянемо кут на плані швидкостей утворений сторонами рк і рs. Сторони цього кута взаємно перпендикулярні напрямку дії сили F і вектору швидкості s точки S ланки ВС. Отже, кут крs дорівнює куту .

Запишемо співвідношення для моменту сили F щодо полюса поверненого плану швидкостей:

(2)

Сторона (кр) є плечем сили F щодо полюса поверненого плану

швидкостей і може бути визначена:

, (3)

Тоді момент сили F відносно полюса р

. (4)

Потужність Рі що утворюється довільною силою Fi визначається за формулою:

, (5)

отже, права частина рівняння (4) є величиною пропорційною потужності.

Тоді запишемо:

(6)

Таким чином, теорема Жуковського доведена.

Зауваження: якщо на ланку діє пара сил, то на повернений план швидкостей треба переносити кожну складову цієї пари окремо.

Маємо можливість також для скорочення записів на важіль Жуковського переносити і моменти діючі на ланки, однак при цьому необхідно виконати їхнє перетворення за наступними формулами:

(7)

де М' - перетворений момент, що прикладаємо до твердого важеля Жуковського, (має розмірність Н*мм).

М - вихідний момент, діючий на ланку механізму, має розмірність .

lBC - довжина ланки ВС, м.

При цьому необхідно мати на увазі наступне: якщо порядок позначень ланки і відповідного їй відрізка поверненого плана швидкостей збігаються, то й напрямок моменту на важелі Жуковського залишаємо без змін. В іншому випадку напрямок моменту необхідно змінити на протилежний.

Наслідок теореми Жуковського. На підставі загального рівняння динаміки сума потужностей усіх зовнішніх сил, прикладених до n ланок механізму і сил інерції ланок дорівнює нулю.

(8)

За умовою теореми Жуковського це рівняння рівносильне рівнянню моментів щодо полюса поверненого плану швидкостей (важеля Жуковського).

(9)

Використовуючи рівняння (9) можна визначити зрівноважувальну силу і зрівноважувальний момент, що прикладені до початкової ланки механізму.

Розглядаємо приклади кінетостатичного розрахунку з використанням методу важіля Жуковського на прикладі механізмів стосовно спеціалізації.

ОСОБЛИВОСТІ АНАЛІТИЧНОГО МЕТОДУ СИЛОВОГО РОЗРАХУНКУ ШАРНІРНО-ВАЖІЛЬНИХ МЕХАНІЗМІВ

1. КРИВОШИПНО-КОРОМИСЛОВИЙ МЕХАНІЗМ

Застосовувати аналітичний метод розв'язання доцільно тільки у випадку, коли попереднє кінематичне дослідження було виконане аналітично. Силове навантаження групи (2-3) першого виду, яка складається з трьох обертальних пар та двох ланок, показано на рис. 3.

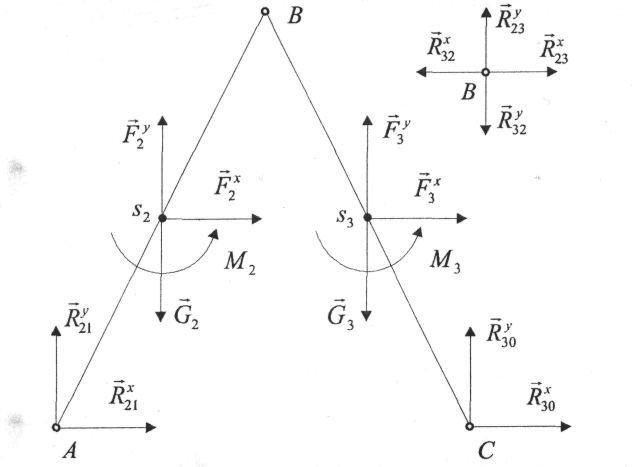
Рис. 3. Силове навантаження групи 2-го класу першого виду:

F2, F3 - сили інерції;

М2 , М3 - моменти сил інерції;

rso, R21 , R30 - реакції в шарнірах А, С;

G2, G3 - сили тяжіння ланок .

Сили представлені у вигляді проекцій F2Х, F2У , F3X, F3Y на відповідні осі. Моменти беремо зі знаком «плюс», коли вони спрямовані проти ходу годинникової стрілки.

Сили взаємодії ланок у кінематичних парах А, С подані у вигляді проекцій на відповідні осі координат. Для їх визначення необхідно скласти рівняння проекцій сил, які діють на групу, а також рівняння моментів сил відносно точки В окремо для кожної ланки. При складанні рівняннь моментів зручно визначати момент сили, наприклад F3, відносно центру моментів на площині, наприклад точки В, за формулою

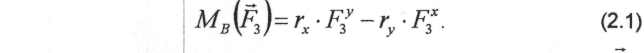
Тут rх, rу - проекції на координатні осі радіуса-вектора, який з'єднує точку В з точкою Sз, де прикладена сила F3. Їх зручно визначати як різницю координат:

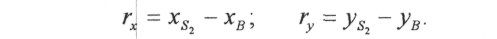
Система рівнянь кінетостатики буде мати вигляд:

Тут хА, уА, уВ, xС, уС, хS2, yS2, xs3, ys3 - координати точок А, В, С, S2, S3, які знайдені при кінематичному дослідженні механізму. Значення реакції R23 y внутрішній кінематичній парі В знаходимо, розглядаючи рівновагу сил, що діють на ланку 2:

Модулі відповідних реакцій знаходимо за формулами:

Відповідні напрямні кути цих векторів визначаємо згідно формул:

2. КРИВОШИПНО-ПОВЗУННИЙ МЕХАНІЗМ

Група 2-го класу 2-го виду та її силове навантаження показані на рис. 4.

Рис. 4. Силове навантаження групи 2-го класу 2-го виду:

F2, F3- сили інерції;

M2, - момент сил інерції;

Rзо, R21 - реакції в кінематичних парах;

G2, G3 - сили ваги ланок.

Аналіз силового навантаження групи (рис. 4) дозволяє зробити висновок, що реакція невідома за величиною і напрямком, а реакція перпендикулярна до осі х, вздовж якої рухається ланка 3. Про те невідоме плече її дії і величина сили.

Для визначення складових , реакції , а також реакції , складаємо рівняння проекцій сил, що діють на групу, а також рівняння моментів цих сил відносно точки В:

Для визначення реакції F23 у кінематичній парі В, розглядаємо рівновагу сил, які діють на одну ланку, наприклад 2:

Модулі реакцій:

Напрямні кути:

3. КУЛІСНИЙ МЕХАНІЗМ

Такий механізм обов'язково містить кулісу. Його різновидом є кривошипно-кулісний механізм, до складу якого входять кривошип і куліса (рис. 5). Його ми і розглянемо. Це механізм 2-го класу 3-го виду. Його силове навантаження представлено на рис. 5.

Масою кулісного каменя - ланки 2, як правило, нехтують. Ланка 2 Рис.2.3. Силове навантаження групи 2-го класу 3-го виду:

знаходиться в рівновазі під дією двох

реактивних сил: . Тому і в проекціях

Оскільки реакція R23 в поступальній парі А перпендикулярна до пінії АВ, то і реакція ; перпендикулярна до тієї ж лінії. Величину визначимо з рівняння моментів сил, які діють на групу ІІ (2-3) відносно точки В

Проекції сили R21 на осі координат:

Реакцію визначаємо з умови рівноваги сил, які діють на групу:

Модуль реакції

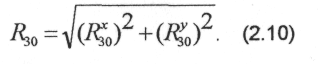
Напрямний кут

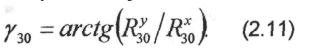
4. СИЛОВИЙ РОЗРАХУНОК ПОЧАТКОВОЇ ЛАНКИ

Силовий розрахунок початкової ланки виконують після визначення реакцій в кінематичних парах груп Ассура, які входять до складу механізму.

Припустимо, що початкова ланка - це незрівноважений кривошип. До нього прикладені (рис.2.4): сила F1 та момент M1 сил інерції; вже знайдена реакція R12 в парі А, невідома реакція в парі О; зрівноважувальний момент Мзр, що забезпечує обертання кривошипу за заданим законом; сила тяжіння кривошипу G1. Величину зрівноважуючого моменту Мзр знаходимо з рівняння моментів сил відносно точки О:

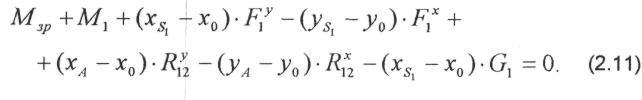
Для визначення реакції в шарнірі О складаємо рівняння проекцій сил на координатні осі:

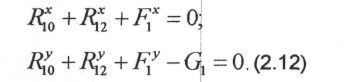
По розв'язанні цих рівнянь відносно проекцiй визначаємо модуль реакції

і її напрямний кут, який утворюється з віссю x

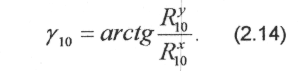
Якщо кривошип зрівноважений, то в рівняння (2.11), (2.12) не будуть входити сили інерції. В перше рівняння не буде входити і сила тяжіння.

Рис.2.4 Силове навантаження початкової ланки:

F1 - сила інерції;

М2 - момент сил інерції;

,- реакції в кінематичних парах;

G1 - сила тяжіння;

Мзр - зрівноважуючий момент

PAGE 1

а) б)

Рис.1.