РАЗРАБОТКА И ИССЛЕДОВАНИЕ АДЕКВАТНОЙ МОДЕЛИ ДВУХМАССОВОГО ДИНАМИЧЕСКОГО СТЕНДА

25

Министерство образования и науки Украины

Донбасская государственная машиностроительная академия

Кафедра _________________________________

РАЗРАБОТКА И ИССЛЕДОВАНИЕ АДЕКВАТНОЙ МОДЕЛИ ДВУХМАССОВОГО ДИНАМИЧЕСКОГО СТЕНДА

(магистерская работа)

Специальность _________________________________

Группа __________________________________

Научный руководитель

____________________________ _____________________

ученая степень, звание Ф.И.О.

Краматорск – 2013

РЕФЕРАТ

Полное название работы: Разработка и исследование адекватной модели двухмассового динамического стенда.

Магистерская работа по специальности: электромеханические системы автоматизации и электропривод.

Студент гр. ЭСА 07зт – маг ДГМА, И.А. Покинтелица. – Краматорск, 2013. Работа содержит 111 стр.: 52 рис., 5 табл.

Объектом исследования является асинхронный двигатель с короткозамкнутым ротором. Предметом исследования является математическая модель, определение статических и динамических характеристик электропривода и определение влияния учета изменяющихся параметров схемы замещения АД. Цель работы – построение рациональных эксплуатационных режимов асинхронного двигателя и выбор системы управления. Для выполнения поставленной цели необходимы решения ряда задач с расчетом параметров, которые повлияют на работу асинхронного двигателя на определенных этапах, ввести в систему управления устройство позволяющее получить оптимальный переходной процесс.

В работе использованы общие методы теории автоматического управления, численные методы, методы математического анализа, математическое моделирование и моделирование с использованием прикладных программ.

В результате исследований были определены параметры схемы замещения асинхронного двигателя, разработана математическая модель, модель была собрана в Matlab Simulink и SimPower System, получены оптимальные графики переходных процессов скорости.

Полученные результаты могут быть использованы в учебном процессе для изучения динамических свойств электропривода, при проектировании и разработке новых систем регулируемых электроприводов.

АСИНХРОННЫЙ ДВИГАТЕЛЬ, РАССЧЕТ ПАРАМЕТРОВ, СХЕМА ЗАМЕЩЕНИЯ, МАТЕМАТИЧЕСКАЯ МОДЕЛЬ, СИСТЕМА УПРАВЛЕНИЯ

РЕФЕРАТ

Повна назва роботи:Розробка та дослідження адекватної моделі двомасового динамічного стенду.

Магістерська робота за фахом: електромеханічні системи автоматизації та електропривод.

Студент гр. ЕСА 07зт – маг ДДМА, І.О. Покинтелиця – Краматорськ, 2013. Робота містить 111 стор.: 52 рис., 5 табл.

Об'єктом дослідження є асинхронний двигун з короткозамкненим ротором. Предметом дослідження є математична модель, визначення статичних та динамічних характеристик електропривода. Мета роботи – побудова раціональних експлуатаційних режимів асинхронного двигуна і вибір системи керування. Для виконання заданої мети необхідні рішення низки завдань з розрахунком параметрів, які вплинуть на роботу асинхронного двигуна на певних етапах, ввести в систему керування пристрій, який дозволить отримати оптимальний перехідний процес.
У роботі використані загальні методи теорії автоматичного керування, чисельні методи, а також методи математичного аналізу, математичне моделювання та

та моделювання з використанням прикладних програм.

У результаті досліджень були визначені параметри схеми заміщення асинхронного двигуна, розроблена математична модель, яка була зібрана в Matlab Simulink і SimPower System, отримані оптимальні графіки перехідних

процесів швидкості.

Результати роботи використані в учбовому процесі при вивченні динамічних властивостей електроприводі, при проектуванні та розробці нових систем регулювання електроприводів.

АСИНХРОННИЙ ДВИГУН, РОЗРАХУНКІВ ПАРАМЕТРІВ, СХЕМА ЗАМІЩЕННЯ, МАТЕМАТИЧНА МОДЕЛЬ, СИСТЕМА КЕРУВАННЯ

REVIEW

The full title of the work: Research and development of an adequate model of the dynamic of the stand.

Master's thesis on the specialty: Electromechanical systems of automation and

electric drive.

Student gr. ESA 07zt – magician DGMA, I.A. Pokinteliza. – Kramators'k, 2013. The work contains 111 pages: 52 figures., 5 tables.

The object of the study is an asynchronous squirrel-cage motor. The subject of the study mathematical model, definition of the static and dynamic characteristics of the electric drive and determination of the influence of the changing parameters of the equivalent circuit asynchronous motor. Purpose – to build rational operational modes of the asynchronous motor and the choice of the control system. To fulfill this goal requires a number of problems with the calculation of the parameters that affect the performance of the asynchronous motor at certain stages, to introduce the control system allows the device to obtain an optimal transition process.

We used the common methods of control theory, numerical methods, mathematical analysis, mathematical modeling and simulation using the application.
Surveys have determined the parameters of the equivalent circuit of the induction motor, a mathematical model, the model was assembled in Matlab Simulink and SimPower System, received the best graphics transient speed.

The results can be used in educational process for the study of the dynamic properties of the drive, the design and development of new systems of adjustable electric drives.

ASYNCHRONOUS MOTOR, CALCULATION OF PARAMETERS, REPLACEMENT SCHEME, MATHEMATICAL MODEL, CONTROL SYSTEM

Міністерство освіти і науки України

Донбаська державна машинобудівна академія

Кафедра ______________________________

Допущено до захисту:

Зав. кафедрою,

____________

РОЗРОБКА ТА ДОСЛІДЖЕННЯ АДЕКВАТНОЇ МОДЕЛІ ДВОМАСОВОГО ДИНАМІЧНОГО СТЕНДУ

магістерська робота (МР) №_________

Напрямок підготовки ___________________________________________

Спеціальність _________________________________________________

Студент гр. _________ ________________ І. О. Покинтелиця

Науковий керівник ________________ В. О. Квашнін

Нормоконтроль ________________ А. М. Беш

Оцінка________________

ECTS_________________

Кількість балів_________

Краматорськ – 2013

Содержание

Перечень условных обозначений, символов, единиц,

сокращений и терминов 8

Введение 9

1 Анализ состояния вопроса 11

1.1 Обзор литературных источников 11

2 Методы исследования 22

2.1 Методы математических исследований 22

2.2. Методика экспериментальных исследований 27

3 Теоретические исследования 30

3.1 Понятие обобщенной электрической машины 30

3.2 Математическое описание асинхронного двигателя как обобщенной электрической машины 33

3.3 Расчет параметров математической модели асинхронного двигателя 44

3.4 Исследование асинхронного двигателя на модели в двухфазной системе координат 50

3.5 Исследование асинхронного двигателя на модели в трехфазной системе координат 56

3.6 Исследование асинхронного двигателя на модели в SimPowerSystems 61

3.7 Исследование двухмассового стенда с асинхронным двигателем на модели в двухфазной системе координат 65

3.8 Исследование двухмассового стенда с асинхронным двигателем на модели в трехфазной системе координат 69

4 Экспериментальные исследования 73

4.1 Виды математических моделей и понятие адекватной модели 73

4.2 Обработка экспериментальных данных. Общие выводы 74

5. Практическое дополнение результатов исследования 81

5.1 Техническая разработка лабораторного стенда на базе асинхронного двигателя АИР56А4У3 81

5.1.1 Назначение установки АИР56А4У3 81

5.1.2 Внешний вид лабораторной установки 81

5.1.3 Устройство и работа установки АИР56А4У3 83

5.2 Охрана труда 85

5.2.1 Анализ вредных и опасных производственных факторов 85

5.2.2 Меры по обеспечению безопасных условий труда 87

5.2.3 Расчет заземления 94

5.3 Экономическое обоснование 98

5.3.1 Сущность и актуальность созданной установки АИР56 98

5.3.2 Анализ предлагаемой лабораторной установки АИР56 98

5.3.3 Расчет капитальных затрат на создание установки АИР56 99

5.3.4 Расчет эксплуатационных затрат лабораторной установки АИР56 101

5.3.5 Обоснование экономической эффективности лабораторной установки 106

Выводы 108

Список используемой литературы 109

ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ, СИМВОЛОВ, ЕДИНИЦ,

СОКРАЩЕНИЙ И ТЕРМИНОВ

ЭВМ – электронно вычислительная машина;

ЭМС – электромеханическая система;

МЧ – механическая часть;

АД – асинхронный двигатель;

АД КЗ – асинхронный двигатель с короткозамкнутым ротором;

ПЧ – преобразователь частоты;

АИН – автономный инвертор напряжения;

ШИМ – широтно-импульсная модуляция;

ПК – программируемый контроллер;

АВП – асинхронный векторный привод;

СИЗ – средства индивидуальной защиты;

ПУЭ – правила устройства электроустановок;

ОиВПФ – опасные и вредные производственные факторы;

ГОСТ – государственный стандарт;

СНиП – строительные нормы и правила.

ВВЕДЕНИЕ

Современные системы векторного управления прошли долгий путь развития и в настоящее время являются наиболее распространенными среди систем электропривода переменного тока. Они позволяют просто и эффективно управлять такими сложными объектами как асинхронный двигатель с короткозамкнутым ротором (АД), что в свою очередь, позволяет существенно расширить область его применения, почти полностью вытесняя из автоматизированных управляемых приводов двигатели постоянного тока. Это связано в первую очередь с развитием силовой электроники, позволяющей создавать надежные и относительно дешевые преобразователи, а также с развитием быстродействующей микроэлектроники, способной реализовать алгоритмы управления практически любой сложности. Поэтому высококачественный асинхронный векторный электропривод в настоящее время является по существу техническим стандартом.

Первым этапом процесса развития АВП была разработка универсальной векторно-матричной математической модели, получившей название обобщенной электрической машины, которая началась в конце 20-х годов и завершилась в конце 40-х годов ХХ века. Эта модель позволяет описывать электромагнитные процессы в идеализированной электрической машине с помощью аппарата линейной алгебры. Практическое использование модели было отложено на несколько десятилетий, т.к. при ручных расчетах она не давала каких-либо преимуществ, но требовала существенных вычислительных затрат, теоретически же ее успешно использовали для анализа переходных процессов в электрических машинах.

Был предложен принцип построения системы управления асинхронным двигателем, в котором использовалась векторная модель АД с ориентацией системы координат по потокосцеплению ротора. Сущность предложенного метода, получившего впоследствии название векторного, заключалась в использовании в системе управления передаточных функций обратных по отношению к передаточным функциям векторной модели АД, что позволяло получить в качестве независимых входных переменных системы величины, входящие в уравнение электромагнитного момента. Поэтому этот принцип называется также прямым управлением моментом. Кроме того, для упрощения задачи в векторной модели АД использовалась система координат, ориентированная по одному из векторов, входящих в уравнение электромагнитного момента, что существенно упрощало передаточные функции системы и позволяло определить момент двумя независимыми переменными аналогично тому, как это делается в двигателях постоянного тока

1. АНАЛИЗ СОСТОЯНИЯ ВОПРОСА
   1. Обзор литературных источников

Создание математических моделей электрических машин для установившихся и переходных режимов – важная задача математической теории электрических машин, так как, при помощи уравнений, достаточно точно описывающих процессы преобразования энергии в ЭП, позволяет изучать поведение и реакцию приводов в различных режимах работы и при различных воздействиях на них. Математическое моделирование является одним из основных этапов проектирования ЭП, который позволяет.

Поэтому построение точной математической модели электропривода и исследование динамики переходных процессов различных режимов работы ЭМО является актуальной задачей.

Копылов И. П. – доктор технических наук, обогатил отечественную электромеханику фундаментальными работами в области динамики электрических машин. Им создана теория обобщенного электромеханического преобразователя, обеспечивающая составление математических моделей для любого случая, встречающегося в практике электромашиностроения. Предложено определение активной, реактивной и обменной мощности в переходных процессах. И.П. Копылов один из первых в стране применил вычислительные машины для решения задач электромеханики [1].

Свои достижения в области динамики электрических машин И.П. Копылов изложил в выдержавшем четыре издания учебнике "Математическое моделирование электрических машин", который в 1990 году удостоен Государственной премии.

В своей работе Копылов моделирование асинхронного двигателя рассматривает как моделирование идеализированных обобщенной двухфазной и трехфазной машин в различных системах координат и в различных формах электрических полей.

Математическую модель обобщенной двухфазной машины Копылов описывает при помощи уравнений Кирхгофа [2]:

(1.1)

При исследовании обобщенной машины рассматривается приведенная электрическая машина (число витков обмоток статора и ротора имеют одинаковое число витков). Предполагается, что имеется рабочий поток, сцепленный с обмоткой статора и ротора, и потоки рассеяния, связанные только с одной обмоткой ротора или статора.

Уравнения записываются для неподвижной машины. Однако чтобы сохранить инвариантность мощности в реальной машине и машине с неподвижными обмотками, в уравнении вводят ЭДС вращения для обмотки ротора.

Система уравнений напряжения и движения описывает процессы электромеханического преобразования и в трехфазной машине только большим количеством уравнений (для каждой фазы). Также могут быть записаны уравнения и для многофазных ЭМ. Однако во всех случаях, когда допустимо преобразование многофазной машины к двухфазной, это необходимо делать.

Ключев В. И. «Теория электропривода» - в книге изложены общие вопросы теории автоматизированного электропривода, рассмотрены свойства разомкнутых и замкнутых электромеханических систем, основы их выбора, приведены методы проектирования приводов [3].

Ключев также описывает электромеханический преобразователь в структуре электропривода как идеализированный двигатель, ротор которого не обладает механической инерцией, не подвержен воздействию момента механических потерь и жестко связан с реальным ротором, входящим в состав механической части электропривода.

Как правило, двигатели являются многофазными электрическими машинами. Однако анализ процессов в многофазной машине стремятся сводить к анализу тех же процессов в эквивалентной двухфазной модели этой машины.

Динамика обобщенной машины описывается четырьмя уравнениями электрического равновесия в цепях ее обмоток и уравнением электромеханического преобразования энергии, которое выражает электромагнитный момент машины М как функцию электрических и механических координат системы, в системе координат, жестко связанной с неподвижным статором (, ), с ротором (d, q).

Уравнения Кирхгофа, выраженные через потокосцепления , имеют вид:

(1.2)

где Rs и Rr – активное сопротивление фазы статора и приведенное активное сопротивление фазы ротора машины.

Достоинством такого математического описания процессов электромеханического преобразования энергии является то, что в качестве независимых переменных в нем используются действительные токи обмоток обобщенной машины и действительные напряжения их питания. Такое описание динамики системы дает прямое представление о физических процессах в системе, однако является сложным для анализа.

Для упрощения математического описания процессов электромеханического преобразования энергии используют линейные преобразования исходной системы уравнений, при этом осуществляются замена действительных переменных новыми переменными при условии сохранения адекватности математического описания физическому объекту.

Так как к электроприводу переменного тока подается трехфазное напряжение, то для перехода от трехфазной машины к двухфазной используется преобразователь напряжений.

Уравнения механической характеристики представляют системе координат u, v, вращающейся с произвольной скоростью, в следующем виде

(1.3)

В соответствии с данными уравнениями собирают модель двигателя, представленную на рисунке 1.1 в виде структурной схемы

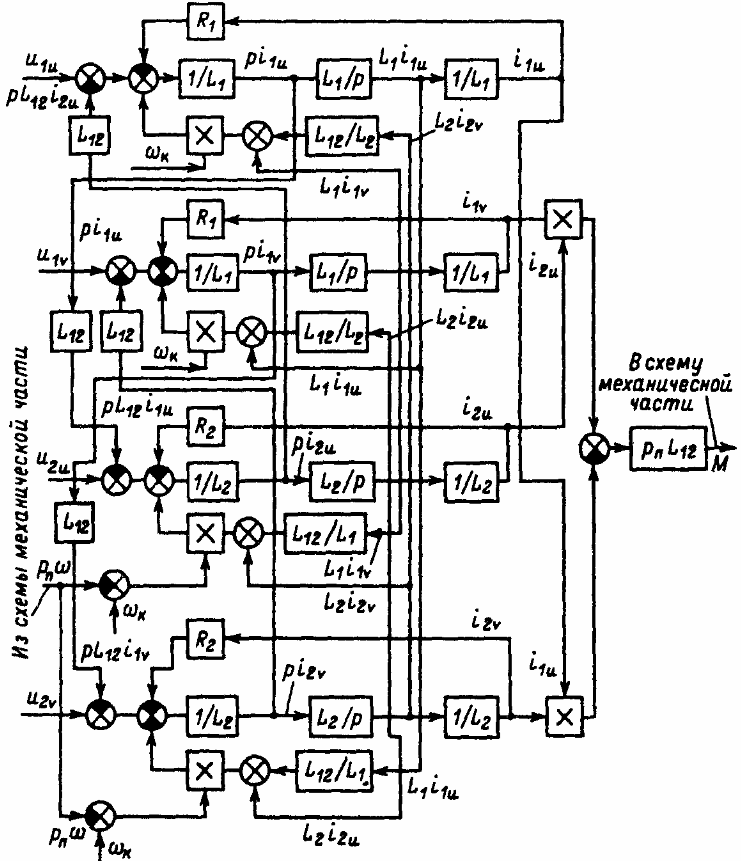
Рисунок 1.1 – Структурная схема динамической модели ЭП в соответствии c уравнениями

Данная модель позволяет изучать динамические процессы в электроприводе.

Однако, по рисунку 1.1 видно, что структура довольно сложная, так как имеет большое количество перекрестных связей, а также она не позволяет моделировать различные аварийные режимы и изучать поведение двигателя при их возникновении.

Башарин А.В., Новиков В. А., Соколовский Г. Г. – выпустили книгу «Управление электроприводами» в 1982 г, в которой рассматривают принципы построения автоматических систем управления электроприводами. Приводят математическое описание двигателей, преобразователей и других типовых узлов как элементов АСУ. Рассматривают типовые системы стабилизации скорости, программные и следящие системы управления электроприводом, а также системы регулирования тока, момента и других параметров [4]. Излагают методы расчета и освещают вопросы машинного проектирования систем управления электроприводом.

Соколовский Г. Г. « Электроприводы переменного тока с частотным регулированием» [5]. В своей книге автор представил математическое описание электропривода с асинхронным двигателем и разомкнутой системой регулирования, математическое описания электропривода с асинхронным двигателем и разомкнутой системой управления в виде структурных схем, электроприводы с синхронными и вентильно-индукторными двигателями, преобразователи частоты в системе частотного регулирования скорости электропривода переменного тока, электроприводы с вентильными двигателями на основе синхронных машин с постоянными магнитами. Обосновал принципы регулирования скорости электроприводов переменного тока изменением частоты вращения на статоре. Системы регулирования скорости электроприводов переменного тока изменением частоты напряжения на статоре. Привел примеры расчета в приводах переменного тока.

Соколовский рассматривает математическое описание ЭП при различном представлении двигателя: в виде Т-образной схемы замещения и трехфазной системы, описанной пространственными векторами.

Онищенко Г. Б. «Электрический привод» - в книге излагаются общие представления об автоматизированном электроприводе, сведения о составе и принципах построения электроприводов, свойствах и характеристиках ЭП с двигателями постоянного и переменного тока, принципах управления ЭП, об элементной базе и современных системах регулируемого ЭП, приводятся общие подходы к выбору и проектированию электроприводов [6].

Усольцев А.А. «Частотное управление асинхронными двигателями».

Пособие содержит основные положения теории частотного управления

асинхронными двигателями и математические модели асинхронного двигателя с короткозамкнутым ротором в векторном представлении, а также принципы построения современных систем модульного и векторного управления асинхронным электроприводом, основанные на этих моделях [7].

В.А. Иванов и А.С. Ющенко занимались разработкой частотных методов исследования линейных импульсных автоматических систем при детерминированных и случайных входных воздействиях, а также методов исследования нелинейных дискретных систем, таких как метод гармонической линеаризации, метод фазовой плоскости. Были проведены исследования устойчивости с помощью прямого метода Ляпунова[4].

В.В. Панкратов занимается разработкой современной теории векторного управления электроприводами на базе асинхронных двигателей с короткозамкнутым ротором и транзисторных преобразователей частоты. Рассматриваются математические модели асинхронного двигателя и транзисторных преобразователей как объектов автоматического управления, принципы непосредственного и косвенного ориентирования вектора управляющих воздействий по магнитному полю двигателя, алгоритмы автоматического управления электромагнитным моментом и скоростью асинхронного электропривода. Значительное внимание уделено допущениям, принимаемым при выводе уравнений объектов, вопросам структурного и параметрического синтеза систем управления [5].

А.Б. Виноградов рассматривает математические основы, структуры, алгоритмы и современные средства управления электроприводами переменного тока: асинхронными, синхронными, вентильно-индукторными. Основное внимание уделено векторным подходам к управлению электроприводами, в основу которых положен метод векторного представления переменных в пространстве состояний. С использованием понятия результирующего вектора и координатных преобразований рассмотрены различные варианты математического описания электродвигателей переменного тока: асинхронных, синхронных, индукторных, в том числе с учетом эффекта насыщения элементов магнитной системы, потерь в стали и поверхностного эффекта [6].

На уровне математических выражений, структурных, функциональных схем и блок-схем алгоритмов работы рассматривает различные варианты построения систем управления электроприводами переменного тока асинхронными, синхронными, вентильно-индукторными. Кроме традиционного подхода к векторному управлению с прямой и косвенной ориентацией при цифровой реализации изучает цифровое релейно-векторного управление, цифровое адаптивно-векторное управление с использованием и без использования датчика углового перемещения.

Отдельное внимание Виноградов уделяет таким вопросам, как идентификация переменных и параметров двигателей, адаптация параметров системы управления к изменению параметров силовой части привода в процессе его работы, векторному управлению активным IGBT-выпрямителем.

Герман-Галкин С. Г. «Компьютерное моделирование полупроводниковых

систем в MatLab 6.0» – в книге рассмотрены вопросы практического использования в MatLab 6.0 для решения задач по проектированию полупроводниковых систем электропривода [8]. Содержит основы электропривода, моделирование систем в пакете «Matlab 6.0 Simulink», силовые полупроводниковые преобразователи, электроприводы постоянного тока, электроприводы переменного тока.

Черных И. В. «Моделирование электротехнических устройств в MatLab SimPowerSistems и Simulink» [9]. В книге содержится описание прикладной программы Simulink и библиотеки блоков SimPowerSistems. Рассматриваются методика создания моделей с помощью графического интерфейса программы, описаны методы расчета моделей, подробно освещена методика создания электротехнических блоков пользователя. Рассмотрен механизм выполнения расчета моделей.

Построение модели линейного асинхронного двигателя с помощью программы «ELCUT» и «FEMLAB» –Живоглядов Е.В., Черных И.В.

Стремительное развитие электронно-вычислительной техники и вместе с тем программного обеспечения к ней, дают возможность решать чрезвычайно большие задачи по расчету статических и динамических характеристик объектов [10].

Существует много программ позволяющих использовать принцип визуального программирования, в соответствии с которым пользователю не требуется записывать системы уравнений и программировать методы их решения, а достаточно лишь создать в графическом редакторе геометрическую модель рассчитываемого устройства, с последующей задачей свойств и параметров решаемой задачи. В итоге получаемые результаты являются достаточно точными и весьма наглядными.

В данной статье был проведен краткий обзор и анализ двух пакетов про-

грамм, при решении задачи магнитного поля переменных токов, это –“ELCUT” и “FEMLAB”.

ELCUT и FEMLAB –это мощные современные комплексы программ для инженерного моделирования, которые решают системы нелинейных дифференциальных уравнений в частных производных методом конечных элементов в одном, тдвух, а “FEMLAB” еще и в трех измерениях, где более наглядно показаны процессы (в зависимости от типа задачи), происходящие в построенной модели. Обе программы позволяют решать двумерные плоские и осесимметричные задачи.

Результатами расчета, в обоих пакетах, являются: векторный магнитный потенциал, плотность тока, напряжение, магнитная индукция, напряженность магнитного поля, силы, моменты, омические потери, вектор Пойнтинга, энергия магнитного поля, импеданс, собственные и взаимные индуктивности.

Можно использовать специальные возможности для отображения полученных данных в интересующей точке модели с помощью интегрального калькулятора, вычисляющего различные интегральные значения на проведенных линиях и поверхностях. В “ELCUT”, два мастера помогают вычислить собственную и взаимную индуктивность катушек и импеданс проводников (полное комплексное сопротивление переменному току).

Очень важно отметить, что “FEMLAB” позволяет интегрировать структуру

модели и полученные данные в пакет “MATLAB” и “SIMULINK”.

Меркушев Дмитрий Викторович. Разработка и исследование принципов построения оптимальных систем управления асинхронными двигателями.

В ходе работы были разработаны принципы построения оптимальных систем управления асинхронным электроприводом, позволяющих минимизировать потери энергии при управлении асинхронным двигателем и способствующих созданию высокотехнологичных производств [11].

Проведен анализ и исследование принципов построения электроприводов с асинхронными двигателями и разработка уточненной математической модели двигателя; синтезирована математическая модель оптимального по энергопотерям регулятора для управления асинхронным двигателем; проанализирована и разработана система оптимального управления асинхронным приводом; разработан датчик момента асинхронного двигателя и использование искусственной нейронной сети для определения электромагнитного момента асинхронного двигателя; разработана методика определения параметров схемы замещения асинхронного двигателя и создана подсистема определения параметров схемы замещения для системы оптимального управления асинхронным двигателем.

Проводимые исследования базировались на положениях технической кибернетики, методах математического моделирования поведения системы управления, теории оптимального управления, теории нечетких множеств, теории искусственных нейронных сетей.

Для имитационного моделирования применялась среда компьютерного математического моделирования MATLAB + SIMULINK. При синтезе оптимального регулятора применялся пакет символьной математики MAPLE.

Математическое описание процессов электромеханического преобразования энергии в электрических машинах основано на составлении и решении дифференциальных уравнений Кирхгофа.

Наиболее полное исследование процессов электромеханического преобразования энергии в асинхронном двигателе предполагает учет как свойств электро- и магнитопроводящих материалов, так и форм, размеров конструктивных элементов и их технологические допуски. Задача очень сложная и предполагает исследование распределения магнитного поля во всех элементах асинхронного двигателя на каждом шаге интегрирования дифференциальных уравнений с учетом эффектов насыщения, вытеснения токов в зависимости от размеров и формы пазов, протекания вихревых токов

При составлении и решение этих дифференциальных уравнений неизбежно встает вопрос о рациональной идеализации параметров и нелинейных зависимостей.

Общепринятыми допущениями при составлении и решении дифференциальных уравнений являются:

- распределенные обмотки статора и ротора заменяется сосредоточенными с идеальными пассивными элементами схем замещения: активными сопротивлениями фаз статора, индуктивностями рассеяния фаз статора и ротора , индуктивностями самоиндукции фаз статора и ротора и максимальной величиной индуктивности взаимной индукции между фазой статора и фазой ротора соответственно.

- для трехфазной симметричной неявнополюсной электрической машины величины собственных индуктивностей фаз статора и ротор равны между собой и равны максимальной величине взаимной индуктивности между фазой статора и ротора, при условии что все параметры ротора приведены к числу витков статора.;

- толщина листов сердечника статора и ротора настолько мала, что можно пренебречь потерями от вихревых токов и на гистерезис;

- статор и ротор имеют симметричные трехфазные обмотки, без нулевого провода, и питаются системой трехфазного симметричного тока, сдвинуты на 120;

- магнитное поле плоскопараллельное, рабочее поле и поля рассеяния

взаимно независимы;

- величины активных сопротивлений и индуктивностей не зависят от частоты питания.

2 МЕТОДЫ ИССЛЕДОВАНИЙ

2.1 Методы математических исследований

Математическое моделирование в настоящее время получило широкое применение при анализе динамики и синтезе электромеханических систем. Аналитическое моделирование электромеханических систем на основании точных методов решения дифференциальных уравнений позволяет обеспечить отсутствие погрешности в отличие от численных методов.

В данном разделе предложено описание аналитических методов математического моделирования электромеханических систем, которые используются для следующих основных в режимов работы двигателей – пуск, торможение, реверс, наброс и сброс нагрузки [16].

Для анализа динамики предлагаются системы дифференциальных уравнений, представленные в нормальной форме Коши. Подробно рассмотрены применения для задач математического моделирования классического метода с отысканием собственных значений и собственных векторов матрицы коэффициентов, операционного метода, метода определителей Вандермонда. В качестве базового программного продукта при решении задач моделирования предлагается использовать MathCAD.

В общем случае электромеханические системы делятся на линейные и нелинейные. Линейная электромеханическая система – это такая система, в которой основные характеристики (по управлению и возмущению) описываются линейными функциями, а саму систему можно представить состоящей из типовых динамических звеньев. В свою очередь, нелинейная электромеханическая система – это система, содержащая хотя бы один нелинейный элемент, то есть элемент, в котором связь между входом и выходом описывается нелинейной функцией.

Электромеханическая система могут работать в двух режимах – статике и динамике. Основной интерес для математического моделирования представляет динамика – неустановившееся состояние ЭМС при переходе из одного устойчивого положения в другое под действием внешних вынуждающих сил. Динамическое состояние любой электромеханической системы описывается системой дифференциальных уравнений. Статика – это такой режим работы электромеханической системы, когда производные всех координат системы равны нулю, то есть координаты системы не меняются по величине со временем (установившийся режим). Для получения уравнений, описывающих статический режим работы электромеханической системы, достаточно в систему дифференциальных уравнений для динамического режима приравнять производные координат электромеханической системы к нулю.

Основной задачей математического моделирования электромеханической системы является решение описывающей ее системы дифференциальных уравнений и дальнейший анализ этого решения.

Существует два основных вида методов решения системы дифференциальных уравнений – аналитические и численные. Линейные электромеханические системы описываются линейными дифференциальными уравнениями, которые могут быть решены как аналитическими, так и численными методами. Различие этих методов состоит в том, что при использовании численных методов решение системы дифференциальных уравнений является несколько неточным. Аналитические же методы позволяют получить точное решение, не содержащее погрешность. Нелинейные электромеханических систем описываются нелинейными дифференциальными уравнениями, для решения которых применимы только численные методы. В данном пособии рассматриваются только аналитические методы решения линейных электромеханических систем.

Представление моделей электромеханических систем в пространстве состояний. Предполагают, что электромеханическая система имеет ряд переменных состояний х1, х2, …, хn. Переменные состояния – это те величины, которые определяют энергетическое состояние электромеханической системы. В качестве таких величин могут выступать токи через катушки индуктивности, напряжения на конденсаторах, скорости вращения двигателей.

Математическую модель электромеханической системы можно представить в виде системы дифференциальных уравнений 1-го порядка, записанной в нормальной форме Коши. Модели электромеханической системы в пространстве состояний пригодны для анализа всех динамических режимов работы: пуска, торможения, реверса, наброса и сброса нагрузки. В результате математического моделирования можно получить статические и динамические характеристики электромеханической системы.

Для этого используют следующие методы решения дифференциальных уравнений.

Классический метод решения систем дифференциальных уравнений. При использовании этого метода необходимо уметь решать систему линейных алгебраических уравнений. Можно отдельно выделить несколько методов решения – точные и итерационные. К точным методам относят методы Гаусса, Крамера и метод обратной матрицы, а к итерационным – метод простых итераций, метод Якоби, методы Зейделя и др. Недостатком итерационных методов является погрешность решения.

Операторный метод решения систем дифференциальных уравнений. Более распространенным по сравнению с классическим является операторный метод решения системы дифференциальных уравнений, основанный на прямом и обратном преобразованиях Лапласа. Эти преобразования позволяют перейти от временных функций к функциям некоторого комплексного переменного и заменить операции дифференцирования и интегрирования соответственно умножением и делением на p. В итоге дифференциальные уравнения превращаются в алгебраические, что значительно упрощает решение.

Решение систем дифференциальных уравнений с применением специальных теорем. Используется в тех случаях, когда входное воздействие электромеханической системы имеет сложный вид, то есть не является функцией Хевисайда, линейной или гармонической функцией, для решения системы дифференциальных уравнений с нулевыми начальными условиями удобно использовать специальные теоремы, к которым относятся интеграл Дюамеля и теорема Бореля. Эти два метода позволяют решить дифференциальные уравнения со сложной правой частью без нахождения ее изображения.

В качестве программного пакета для моделирования полупроводниковых электроприводов наиболее подходящей считается система MatLab (матричная лаборатория) со своими пакетами расширения (Toolboxes), повсеместно принятая в качестве основного инструмента изучения полупроводникового электропривода. Основной объект системы MATLAB - прямоугольный числовой массив (матрица), в котором допускается применение комплексных элементов. Использование матриц не требует явного указания их размеров.

Система MATLAB обеспечивает выполнение операций с векторами и матрицами даже в режиме непосредственных вычислений. Ею можно пользоваться как мощнейшим калькулятором, в котором наряду с обычными арифметическими и алгебраическими действиями могут использоваться такие сложные операции, как обращение матрицы, вычисление ее собственных значений и векторов, решение систем линейных алгебраических уравнений и много других. Характерной особенностью системы является ее открытость, то есть возможность ее модификации и адаптации к конкретным задачам пользователя.

Привлекательной особенностью системы MATLAB является наличие встроенной матричной и комплексной арифметики. Система поддерживает выполнение операций с векторами, матрицами и массивами данных, реализует сингулярное и спектральное разложение, расчет ранга и чисел обусловленности матриц, поддерживает работу с алгебраическими полиномами, решение нелинейных уравнений и задач оптимизации, интегрирование функций в квадратурах, численное интегрирование дифференциальных и разностных уравнений, построение различных графиков, трехмерных поверхностей и линий уровня.

MATLAB предоставляет широкие возможности для работы с сигналами, для расчета и проектирования аналоговых и цифровых фильтров, включая построение их частотных, импульсных и переходных характеристик. Имеются в системе и средства выполнения спектрального анализа и синтеза, в частности реализации прямого и обратного преобразования Фурье. Благодаря этому ее довольно удобно использовать при проектировании электронных устройств.

Основными пакетами расширения, которые использованы при исследовании полупроводникового электропривода, являются Simulink и Power System Blockset [23].

Одной из наиболее привлекательных особенностей системы MATLAB является наличие в ней наглядного и эффективного средства составления программных моделей - пакета визуального программирования Simulink.

Пакет Simulink со своими дополнениями – основной инструмент изучения различных электромеханических систем. Практически не существует задачи, связанной с исследованием систем электропривода, которую нельзя было бы решить в этом пакете. Simulink предоставляет исследователю самые различные возможности, начиная от структурного (математического) представления системы и кончая генерированием кодов для программирования микропроцессора в соответствии со структурной схемой модели. Библиотека Simulink представляет собой набор визуальных объектов, используя которые можно исследовать практически любую систему автоматического регулирования. Практически для всех блоков существует возможность настройки параметров. Параметры настройки отражаются в панели окна настройки выбранного блока. Пакет Simulink позволяет осуществлять исследование (моделирование во времени) поведения динамических линейных и нелинейных систем, причем составление «программы» и ввод характеристик систем можно производить в диалоговом режиме, путем сборки на экране схемы соединений элементарных звеньев. В результате такой сборки получается модель системы, называемая S-моделью. В качестве «кирпичиков» при построении S-модели применяются визуальные блоки (модули), которые сохраняются в библиотеках Simulink. S-модель может иметь иерархическую структуру, то есть состоять из моделей более низкого уровня, причем количество уровней иерархии практически не ограничено.

2.2 Методика экспериментальных исследований

При помощи аналитических методов выбирается релевантная информация из всей имеющейся, которая получена в результате первичной обработки конкретных данных.

Метод – это совокупность приемов или операций практического или теоретического освоения действительности, подчиненных решению конкретной задачи. Фактически разница между методом и теорией имеет функциональный характер, формируясь как теоретический результат предыдущего исследования, метод является исходным пунктом и условием будущих исследований.

Наблюдение – это систематическое, целенаправленное изучение объекта. Чтобы быть эффективным, наблюдение должно отвечать следующим требованиям:

- задуманное заранее ( наблюдение проводится для определенной четко поставленной задачи),

- планомерность (выполняется по плану, составленным соответственно поставленной задаче),

- целенаправленность (наблюдаются лишь определенные стороны явления, вызывающие интерес при исследовании)

- активность ( исследователь активно ищет необходимые объекты. черты, явления)

- систематичность (исследование ведется непрерывно или по определенной системе).

Наблюдение как метод познания позволяет получить первичную информацию в виде совокупности эмпирических утверждений. Эмпирическая совокупность образует первичную схематизацию объектов реальности - исходных объектов научного исследования.

Сравнение – это процесс становления сходства или различия предметов и явлений действительности, а так же нахождения общего, присущему двум или нескольким объектам.

Метод сравнения будет результативным при условиях:

- сравниваются только те явления, между которыми возможна некоторое объективное сходство,

- сравнение должно осуществляться по наиболее важными, существенными (в плане конкретной задачи) чертами,

Разные объекты или явления могут сравниваться непосредственно или косвенно через их сравнение с любым другим объектом (эталоном). У первом случае обычно получают качественные результаты больше – меньше, выше – ниже. Сравнение же объектов с эталоном дает возможность получить количественные характеристики. Такие сравнения называются измерением.

При помощи сравнения информация касающаяся объекта находится двумя способами:

- непосредственный результат сравнения ( первичная информация),

- результат обработки первичных данных (вторичная или производная информация).

Измерение – это определение числового значения определенной величины при помощи единиц измерения. Измерение предусматривает наличие таких основных элементов, объекта измерения, эталона, измерительных приборов, метода измерения. Измерение развилось из операции сравнения, зато оно – более мощное и универсальное познавательное средство.

Эксперимент – это такой метод изучения объекта, при котором исследователь активно и целенаправленно влияет на него благодаря созданию искусственных условий или использованию природных условий, необходимых для определения соответствующего свойства.

Преимущества экспериментального изучения объекта в сравнении с наблюдением:

- в процессе эксперимента можно изучать явление «в чистом виде», освободившись от побочных факторов, которые затеняют основной процесс,

- в экспериментальных условиях можно исследовать свойства объектов,

- можно проводить опыты столько раз, сколько это необходимо.

Эксперимент проводят в случае выявления ранее не известных свойств объекта, при проверке правильности теоретических расчетов, при демонстрации явления.

В научном исследовании эксперимент и теория связаны самым тесным образом, игнорирование эксперимента несомненно приводит к ошибкам, поэтому всестороннее развитие экспериментальных исследований является одним из важных путей развития современной науки.

3 ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ ДВУХМАССОВОГО

ДИНАМИЧЕСКОГО СТЕНДА НА БАЗЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

3.1 Понятие обобщенной электрической машины

Обобщенная электрическая машина (ОЭМ) является математической моделью, описывающей процессы электромеханического преобразования энергии в электрических машинах как переменного, так и постоянного тока. В качестве ОЭМ будем рассматривать систему, входным воздействием для которой является вектор напряжения, подводимого к ее электрическим обмоткам, а выходным – электромагнитный момент, как это показано на рисунке 3.1.

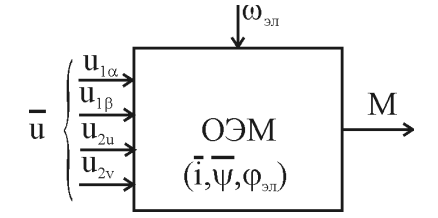
Рисунок 3.1 – Структура обобщенной электрической машины

Внутреннее состояние ОЭМ определяется электрическим током, протекающим по обмоткам, магнитным потоком (потокосцеплением) и взаимным положением обмоток статора и ротора. Угловую скорость вращения ротора будем рассматривать как некоторое независимое внешнее воздействие.

Все электрические машины осуществляют преобразование электрической энергии в механическую, в результате чего на валу двигателя возникает электромагнитный момент. При этом, формирование электромагнитного момента происходит в воздушном зазоре при взаимодействии магнитных полей статора и ротора.

Конструктивно электрические машины выполняют так, что распределение величины магнитного потока, по окружности зазора близко к синусоидальному (рисунок 3.2).

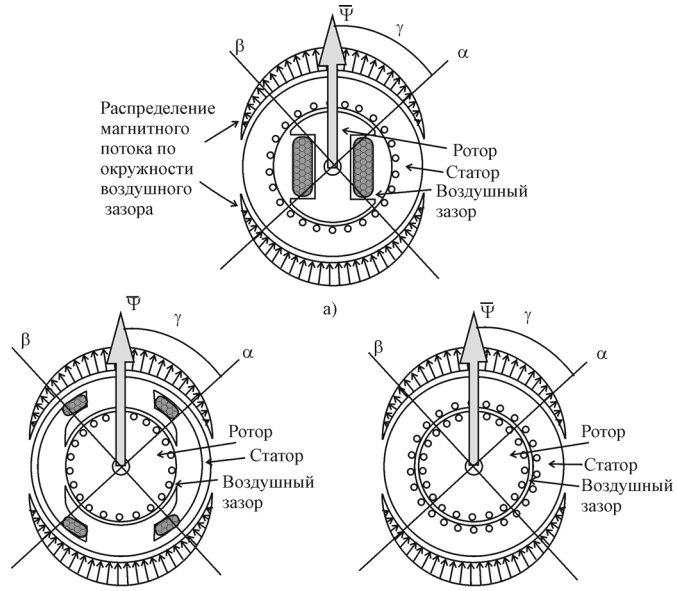
Рисунок 3.2 – Распределение величины магнитного потока

по окружности зазора

Зная, что магнитный поток распределен вдоль окружности воздушного зазора синусоидально, для того чтобы получить картину его распределения по окружности достаточно знать амплитуду магнитного потока (m) и его положение в пространстве, которое определяется углом , относительно некоторой, произвольно выбранной, системы координат. В соответствии с этим, информацию о магнитном состоянии любой электрической машины можно представить в виде вектора, модуль которого по величине равен m, а пространственное положение определено углом (рисунок 3.2).

Следует также отметить, что распределение тока по окружности зазора и напряженности электрического поля внутри проводников обмоток по окружности зазора у электрических машин с неявно выраженными полюсами также распределены синусоидально (рисунок 3.3).

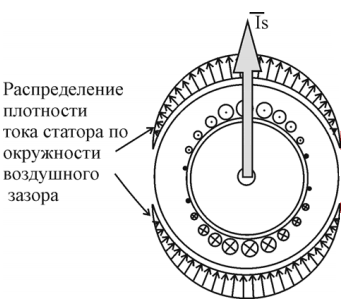
Рисунок 3.3 – Распределение плотности электрического тока вдоль воздушного зазора электрической машины

Таким образом, все электромагнитные переменные любой электрической машины можно представить в виде векторов в плоскости поперечного сечения электрической машины.

Для того, чтобы представить некоторый вектор Х в декартовой системе координат, например обозначенной как - (рисунок 3.4), необходимо и достаточно знать его составляющие х и х. Если на выбранных нами осях координат расположить обмотки, как показано на рисунке 3.4, и принять вектор Х за вектор напряжения, то приложив к обмоткам напряжения по величине равные, соответственно, составляющим х и х, то они сформируют вектор напряжения в плоскости поперечного сечения электрической машины. Таким же образом будут формироваться векторы токов и потокосцеплений. В результате можно сделать вывод, что для описания электромагнитных процессов, протекающих в любой электрической машине, необходимо и достаточно рассмотрение электрической машины, содержащей две обмотки на статоре и две обмотки на роторе, т.е. двухфазной обобщенной электрической машины.

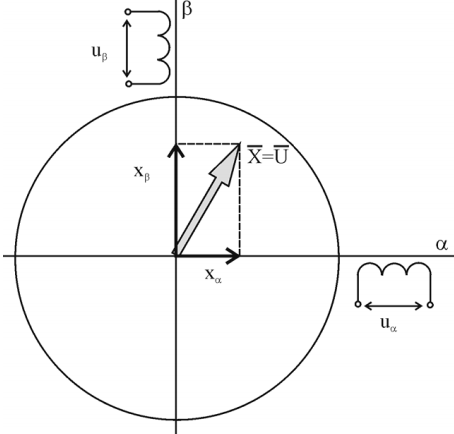
Рисунок 3.4 – Векторная форма представления электромагнитных переменных электрических машин

3.2 Математическое описание асинхронного двигателя как обобщённой электрической машины

При математическом описании асинхронной машины используются общепринятые допущения и ограничения, а именно:

• магнитная система машины не насыщена;
• потери в стали отсутствуют;
• фазные обмотки машины симметричны и сдвинуты строго на 120 (для трехфазных машин);
• магнитодвижущие силы обмоток и магнитные поля распределены вдоль окружности воздушного зазора по синусоидальному закону;
• величина воздушного зазора постоянна;
• ротор машины симметричен;
• реальная распределенная обмотка заменена эквивалентной сосредоточенной, создающей ту же магнитодвижущую силу.

Современный уровень развития вычислительной техники, вообще говоря, дает принципиальную возможность с учетом сделанных допущений строить модель асинхронного двигателя в фазных координатах. Однако структурная схема модели при этом получается весьма сложной из-за наличия переменных коэффициентов в уравнениях связи фазных токов и потокосцеплений машины, зависящих от мгновенного значения угла поворота ротора относительно магнитных осей статора двигателя. С целью упрощения математических моделей систему уравнений трехфазной асинхронной машины, записанную в фазных координатах [8], принято представлять в ортогональной системе координат (х – у), вращающейся в пространстве в общем случае с произвольной угловой скоростью к.

Эквивалентные напряжения статора в системе координат (х – у) связаны с фазными напряжения трехфазной машины следующими соотношениями

(3.1)

Аналогичные соотношения связывают эквивалентные значения токов и потокосцеплений двигателя с соответствующими фазными значениями переменных. Подставляя в эти уравнения выражения для реальных фазных напряжений

(3.2)

можно получить выражения для составляющих напряжений в эквивалентной двухфазной системе координат:

(3.3)

(3.4)

где Um – амплитудное значение фазного напряжения,

о – частота вращения поля статора двигателя в пространстве,

о – начальная фаза напряжения фазы А двигателя.

Система уравнений электромагнитного равновесия асинхронного двигателя в форме Коши в системе координат (х – у) может быть представлена следующим образом:

(3.5)

где sx, sy – потокосцепления эквивалентных статорных контуров;

rx, ry – потокосцепления эквивалентных роторных контуров;

isx,isy – эквивалентные токи статора;

irx, iry – эквивалентные токи ротора;

Rs, Rr – активные сопротивления фазных обмоток статора и ротора;

– частота вращения ротора двигателя.

Для решения этой системы уравнений ее необходимо дополнить уравнениями связи эквивалентных токов и потокосцеплений машины. В системе координат (х – у) эквивалентные потокосцепления и токи статора и ротора двигателя связаны друг с другом следующими уравнениями

где Lm – взаимная индуктивность, учитывающая магнитную связь одной фазы статора с тремя обмотками ротора и соответственно одной обмотки ротора с тремя обмотками статора,

Ls=Lm+Ls – индуктивность обмотки статора, учитывающая магнитную связь с двумя другими фазными обмотками статора,

Lr=Lm+Lr – индуктивность обмотки ротора, учитывающая магнитную связь с двумя другими фазными обмотками ротора,

Ls – индуктивность рассеяния фазной обмотки статора,

Lr – индуктивность рассеяния фазной обмотки ротора.

Коэффициенты в уравнениях связи между эквивалентными токами и потокосцеплениями не зависят от мгновенного значения угла поворота ротора относительно магнитной оси статора двигателя. Для построения математической модели асинхронного двигателя удобнее пользоваться обратными зависимостями, то есть зависимостями i = f(), которые имеют вид

(3.6)

где – коэффициент рассеяния двигателя.

Как было показано выше, выражение для электромагнитного момента асинхронного двигателя представляет собой векторное произведение любой пары пространственных векторов токов и потокосцеплений. Таким образом, в системе координат (х – у) можно использовать шесть уравнений для отыскания электромагнитного момента двигателя. При использовании любого из этих выражений результат, естественно, будет один и тот же

(3.7)

(3.8)

(3.9)

где рп – число пар полюсов асинхронного двигателя.

Выбор того или иного вида уравнения для электромагнитного момента осуществляется из условия рационального построения структурной схемы математической модели.

Уравнение движения двигателя в одномассовой механической системе, как известно, имеет вид

(3.10)

где J – суммарный момент инерции ротора двигателя и механизма;

Мс – статический момент нагрузки электропривода.

Структурная схема асинхронного двигателя в системе координат (х – у) представлена на рисунке 3.5.

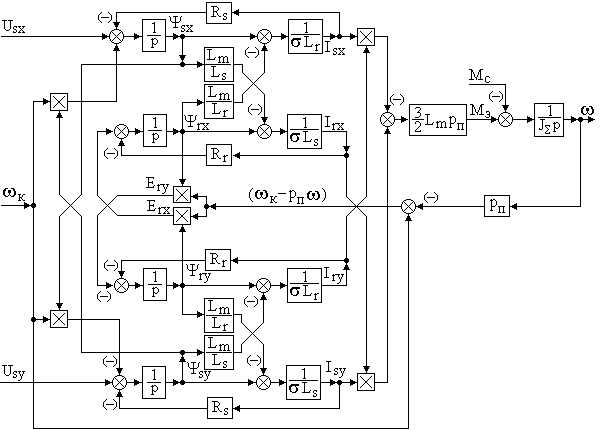
Рисунок 3.5 – Структурная схема асинхронного электродвигателя в системе координат, вращающейся в пространстве с произвольной

угловой скоростью к.

В зависимости от выбора скорости вращения системы координат к уравнения электромагнитного равновесия асинхронного двигателя несколько видоизменяются, однако механическая характеристика двигателя, рассчитанная в системе координат, вращающейся в пространстве с любой угловой скоростью к, изменений не претерпевает.

В теории электромагнитных переходных процессов электрических машин используются три основные координатные системы, являющиеся частными случаями рассмотренной выше.

Первая система координат неподвижна относительно статора двигателя, то есть к = 0. Оси в этой системе координат обозначаются ( – ). Основное преимущество системы координат ( – ) состоит в том, что при выборе положения одной из ее осей (принято – оси ), совпадающим с магнитной осью одной из фаз реальной машины, эквивалентный ток is будет равен реальному фазному току двигателя. Эта система координат широко применяется для анализа систем электропривода с управлением двигательными и тормозными режимами по цепи статора, в том числе и при анализе систем с векторным управлением. Определенную сложность при построении модели асинхронного двигателя в системе координат ( – ) представляет то обстоятельство, что эквивалентные напряжения Us и Us изменяются во времени по синусоидальному закону. В том случае, если частота источника электроэнергии fс постоянна

(3.11)

для формирования гармонических входных сигналов модели могут быть использованы два консервативных звена с передаточными функциями

(3.12)

Переходные функции таких звеньев имеют вид

(3.13)

Эквивалентные составляющие напряжения статора асинхронного двигателя в системе координат ( – ) могут быть получены следующим образом

(3.14)

При исследовании систем электропривода с частотным управлением частота о является величиной переменной. В этом случае для получения составляющих напряжения статора Us и Us необходимо использовать нелинейную модель идеального преобразователя частоты, имеющую следующую структурную схему:

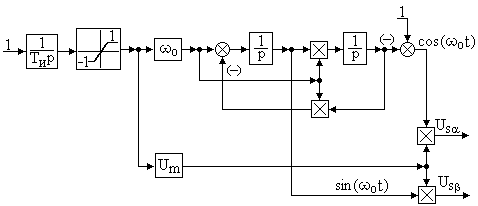
Рисунок 3.6 – Структурная схема идеального преобразователя частоты

В структурной схеме на рисунке 3.6 с помощью интегратора и блока ограничения построен задатчик интенсивности с единичным выходным сигналом. Собственно преобразователь частоты построен с помощью двух интеграторов и двух блоков умножения. На выходе первого интегратора получается синусоидальный сигнал с единичной амплитудой и переменной частотой о. На выходе второго интегратора получается сигнал вида (1–cos оt). С помощью дополнительного сумматора эта функция вычитается из 1 и на выходе сумматора получается косинусоидальный сигнал с единичной амплитудой и переменной частотой о. Посредством второй пары умножителей единичные косинусоидальный и синусоидальный сигналы умножаются на амплитудное значение выходного напряжения преобразователя частоты Um, также являющееся величиной переменной. Обе переменные величины, и частота о, и амплитуда Um формируются с помощью общего задатчика интенсивности, благодаря чему на выходах второй пары умножителей получаются эквивалентные напряжения статора асинхронного двигателя Us и Us при реализации известного закона частотного управления:

(3.15)

При необходимости динамическая модель идеального преобразователя частоты позволяет реализовать также любой другой закон частотного управления асинхронным двигателем. При создании модели асинхронного электропривода на основе преобразователей частоты с широтно-импульсной модуляцией идеализация преобразователя частоты не вносит существенных погрешностей в вычисления, так как токи и потокосцепления в таких системах практически синусоидальны.

На рисунке 3.7 представлена структурная схема математической модели асинхронного двигателя в неподвижной относительно статора системе координат ( – ) при работе от источника питания стабильной частоты.

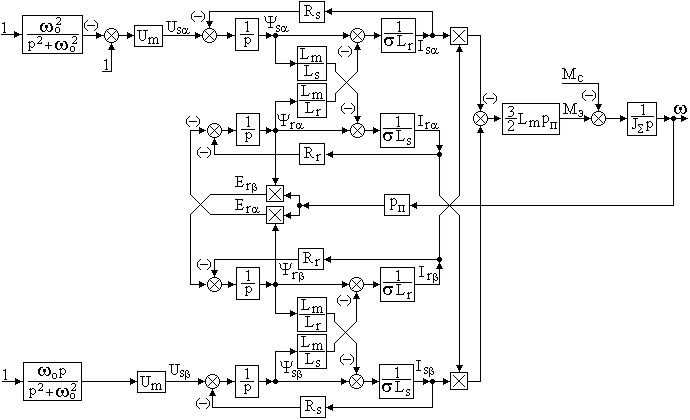
Рисунок 3.7 – Структурная схема асинхронного электродвигателя в неподвижной системе координат ( - )

Несмотря на некоторые сложности при формировании эквивалентных напряжений Us и Us, система координат ( – ) широко применяется при построении систем векторного управления асинхронным электроприводом. В этой системе координат вычисляемые переменные роторной цепи двигателя изменяются во времени по синусоидальному закону с частотой о. Переход от эквивалентных токов по осям и к фазным токам статорных контурных можно выполнить следующим образом

(3.16)

(3.17)

. (3.18)

Переход от эквивалентных токов по осям и к фазным токам роторных контуров выполняется следующим образом

(3.19)

(3.20)

(3.21)

Аналогично может быть осуществлен переход к фазным координатам для остальных статорных и роторных переменных.

Динамическая модель асинхронного двигателя выполнена в неподвижной относительно статора системе координат ( – ), для векторного преобразования, прежде всего, осуществляется вычисление модуля вектора потокосцепления ротора двигателя по формуле:

(3.22)

После этого определяются мгновенные значения косинуса и синуса угла для перевода переменных в систему координат, ориентированную в пространстве по вектору потокосцепления ротора

(3.23)

где  – пространственные угол между мгновенным положением вектора потокосцепления ротора двигателя и осью .

Поскольку вектор потокосцепления ротора вращается в пространстве с частотой источника питания двигателя о, новая система координат также должна вращаться с этой же частотой. Оси в новой системе координат обозначаются (1 – 2), причем принято, что ось 1 совпадает по направлению с вектором потокосцепления ротора.

3.3 Расчет параметров математической модели асинхронного двигателя

Упрощенная математическая модель асинхронного двигателя описывается следующими уравнениями

, (3.24)

, (3.25)

, (3.26)

, (3.27)

где – напряжение на статоре;

– активное сопротивление статора;

– полный ток статора;

– потокосцепление статора;

– угловая частота вращения магнитного поля статора;

– напряжение на статоре;

– активное сопротивление ротора;

– полный ток ротора;

– потокосцепление ротора;

– число полюсов;

– угловая частота вращения ротора;

– взаимная индуктивность между обмотками статора и ротора;

– полная индуктивность фазы статора

, (3.28)

где – индуктивность рассеяния обмотки статора;

– полная индуктивность фазы ротора

, (3.29)

где – индуктивность рассеяния обмотки ротора.

Схема замещения асинхронного двигателя приведена на рисунке 3.8, а данные для расчетов – в таблице 3.1.

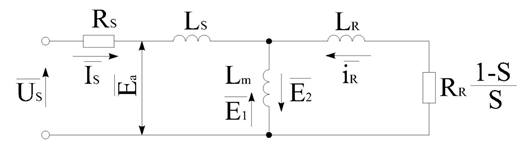
Рисунок 3.8 – Т-образная схема замещения машины

Таблица 3.1 – Исходные данные двигателя АИР56А4У3

Параметр	Значение	Ед. изм.
Мощность	0,12	кВт
Частота вращения	1325	об/мин
Номинальное напряжение	220	В
Номинальный ток	0,76	А
cos при 100% загрузке	0,66
cos при 75% загрузке	0,66
при 100% загрузке	0,565
при 75% загрузке	0,565
Кратность пускового тока	4,6
Кратность пускового момента	2,1
Кратность максимального момента	2,2
Момент инерции	0,0007	кгм2

Расчет Т-образной схемы замещения (рисунок 3.8) электрической машины проведем по исходным данным, представленным в таблице 3.1. Для расчета Т-образной схемы замещения воспользуемся методикой изложенной в [16].

Коэффициент загрузки

. (3.30)

Мощность при данном коэффициенте загрузки:

(3.31)

Синхронная частота сети

(3.32)

Номинальная частота вращения ротора при 50Гц

(3.33)

Номинальный момент

(3.34)

Пусковой момент двигателя

(3.35)

Номинальный ток статора

(3.36)

Пусковой ток

(3.37)

Ток при загрузке двигателя на 75% от номинала

A. (3.38)

Расчетные коэффициенты для расчета тока холостого хода

(3.39)

(3.40)

(3.41)

Ток холостого хода

(3.42)

Предварительное значение жесткости

(3.43)

Конструктивный коэффициент

. (3.44)

Коэффициенты для расчета критического скольжения:

(3.45)

(3.46)

Критическое скольжение

(3.47)

Определение угла сдвига фаз при х.х.

. (3.48)

Активная часть тока

(3.49)

Активная часть тока при х.х.

(3.50)

Расчет коэффициентов для уточнения жесткости механической характеристики:

(3.51)

(3.52)

(3.53)

, (3.54)

(3.55)

(3.56)

(3.57)

Уточненная жесткость механической характеристики АД

(3.58)

Расчет сопротивлений АД Т-образной схемы замещения

(3.59)

(3.60)

(3.61)

(3.62)

(3.63)

Расчет ЭДС в машине

(3.64)

(3.65)

(3.66)

Определение сопротивления взаимоиндукции

(3.67)

Переходные индуктивности статора и ротора

(3.68)

(3.69)

Взаимная индуктивность статора и ротора, приведенная к статору

(3.70)

Индуктивность статора и ротора

(3.71)

(3.72)

Коэффициент магнитной связи статора и ротора:

(3.73)

(3.74)

Коэффициент рассеяния машины

. (3.75)

Представим все расчетные величины в виде таблицы 3.2.

Таблица 3.2 – Расчетные величины

Параметр	Значение	Ед. изм.
Номинальная частота вращения ротора	138,7	с-1
Номинальный момент Мн	0,87	Нм
Пусковой момент Мп	1,827	Нм
Номинальный ток статора Iн	0,53	А
Критическое скольжение sкр	0,745
Сопротивление	активное статора RS	15,52	Ом
	активное ротора RR	37,705	Ом
	реактивное статора XS	20,214	Ом
	реактивное ротора XR	27,915	Ом
Сопротивление взаимоиндукции Xm	161,075	Ом
Полная индуктивность	статора LS	0,577	Гн
	ротора LR	0,691	Гн
Взаимная индуктивность статора и рота приведенная к статору	2,007	Гн
Коэффициент магнитной связи	статора kS	0,89
	ротора kR	0,852
Коэффициент рассеяния машины	0,242

3.4 Исследование асинхронного двигателя на модели в двухфазной системе координат ( – )

В практических расчетах динамики электропривода переменного тока используются различные системы относительных единиц.

Система относительных единиц (англ. per-unit system) – способ расчета параметров в системах передачи электроэнергии, при котором значения системных величин (напряжений, токов, сопротивлений, мощностей и т.п.) выражаются как множители определенной базовой величины, принятой за единицу. Это упрощает вычисления, так как величины, выраженные в относительных единицах, не зависят от уровня напряжения.

Применительно к рассматриваемой задаче удобнее всего использовать систему относительных единиц с равными взаимными индуктивностями между статорными и роторными обмотками, а также между фазными обмотками ротора. Поэтому были приняты базисные величины, приведенные в таблице 3.3. Там же приведены числовые значения параметров динамической модели.

Таблица 3.3 – Базисные величины, принятые для моделирования

Физический параметр	Базисная величина	Выражение для базисной величины	Числовое Значение параметра , о.е.
Напряжение	номинальное амплитудное значение фазного напряжения
Ток	номинальное амплитудное значение фазного тока
Сопротивление	отношение фазного напряжения к фазному току
Частота Вращения	синхронная частота вращения поля статора при номинальной частоте преобразователя частоты
Индуктивность	отношение потокосцепления к току или индуктивного сопротивления к синхронной частоте вращения
Мощность	полная номинальная мощность двигателя		Sном=0,117
Момент инерции	Отношение полной мощности к кубу синхронной частоты вращения

Модель двигателя в системе координат ( – ) приведена на рисунке 3.9.

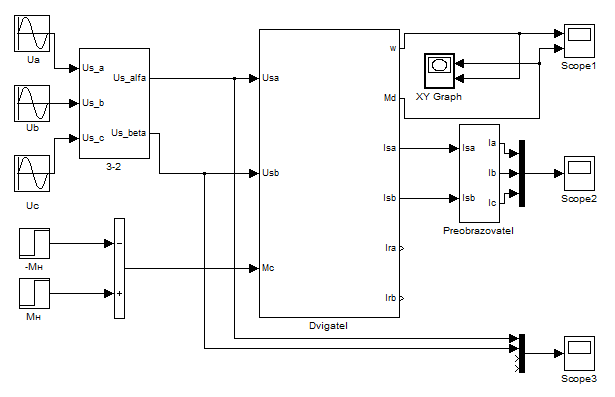
Рисунок 3.9 – Модель двигателя в системе координат ( – )

Собственно, сам двигатель на рисунке 3.9 скрыт в виде маскируемой подсистемы, содержимое которой раскрывается на рисунке 3.10.

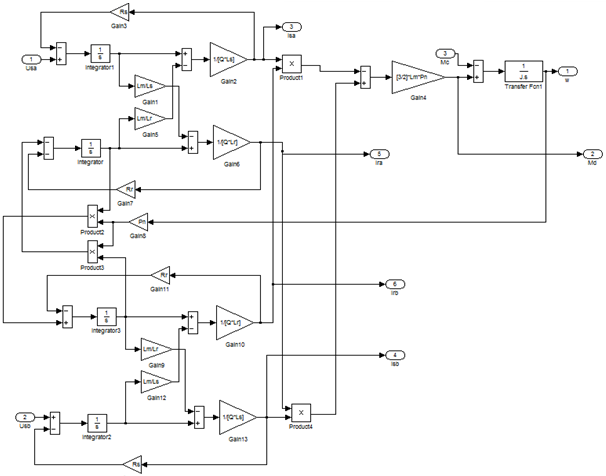
Рисунок 3.10 – Содержимое блока Dvigatel

Параметры схемы замещения, задаваемые при моделировании, показаны на рисунке 3.11. На рисунке 3.12 показана механическая характеристика асинхронного двигателя, полученная в динамике на модели. Переходные функции, снятые на модели, представлены на рисунках 3.13 – 3.16.

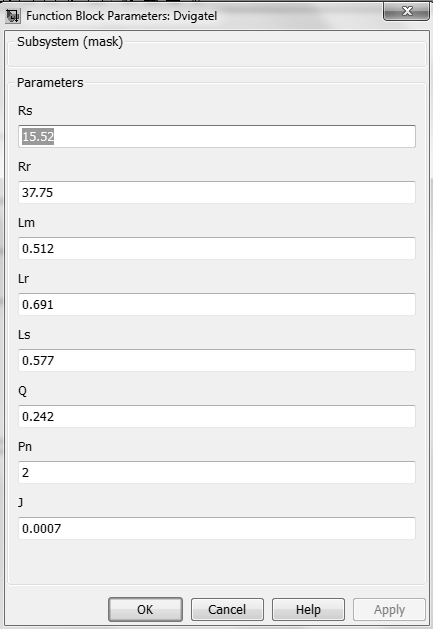
Рисунок 3.11 – Параметры схемы замещения асинхронного двигателя

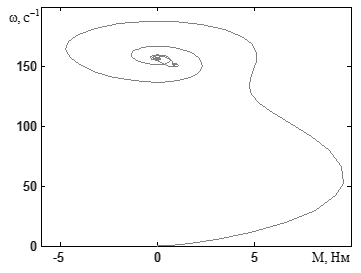
Рисунок 3.12 – Механическая характеристика асинхронного двигателя,

полученная в динамике

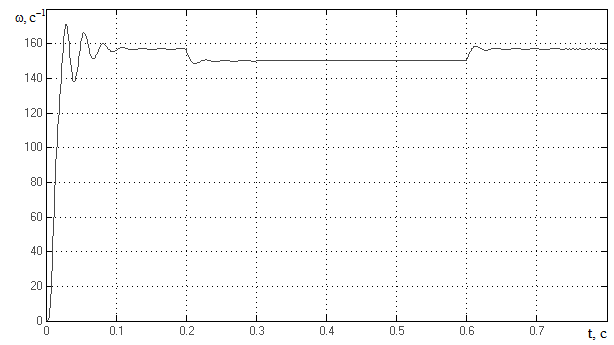
Рисунок 3.13 – Переходный процесс по скорости асинхронного двигателя

Перерегулирование по скорости при пуске составляет

%. (3.76)

Перерегулирование по скорости при набросе нагрузки

%. (3.77)

При набросе нагрузки наблюдается статическая ошибка

%. (3.78)

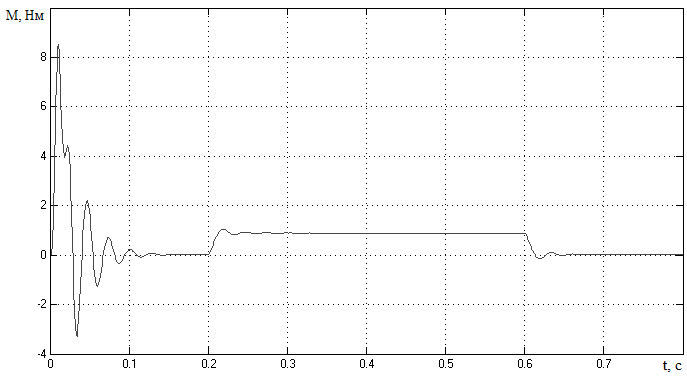
Рисунок 3.14 – Переходный процесс по моменту асинхронного двигателя

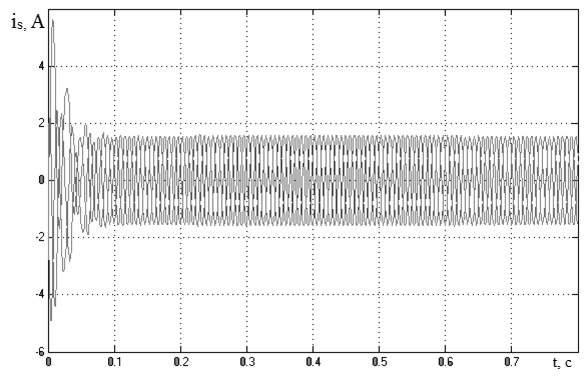
Рисунок 3.15 – Осциллограмма токов статора

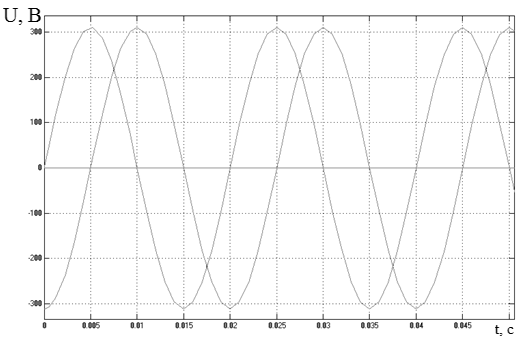
Рисунок 3.16 – Осциллограммы напряжений на выходе

координатного преобразователя

3.5 Исследование асинхронного двигателя на модели в трехфазной системе координат

Обычно исследование асинхронных двигателей (АД), как аналитическое, так и численное, в большинстве случаев базируется на основе прямоугольных систем координат ( – ) , (d – q,) и (u – v), которые получаются после преобразований естественной системы координат 3-фазного асинхронного двигателя (АД), так как исследование динамических характеристик АД в трехфазной непреобразованной системе координат более сложно. Но изучение динамических режимов работы АД в таких искусственных системах координат ведет к потере непосредственной информации о токах в фазах статора и ротора. В трехфазной же системе мы имеем дело с реальными фазными величинами токов. Для анализа АД с управлением от полупроводниковых преобразователей, характеризующихся переменной структурой силовой цепи со сложным и иногда прерывистым характером электромагнитных процессов, целесообразно в качестве математической модели использовать систему дифференциальных уравнений в фазных заторможенных координатных осях.

Применение указанной модели особенно, при анализе преобразователей частоты с ШИМ, позволит, с одной стороны, получить реальные динамические процессы изменений напряжений и токов в полупроводниковых ключах при их коммутации, правильно определить интервалы включенного и выключенного состояния тиристоров, а с другой стороны, достоверно рассчитать токи и все необходимые характеристики электромеханической системы с АД. Для описания процессов в частотно-управляемых АД следует использовать 3-фазные системы координат, потому что преобразованные токи и напряжения статора не отражают реальную картину коммутационных и электромагнитных процессов в силовой цепи.

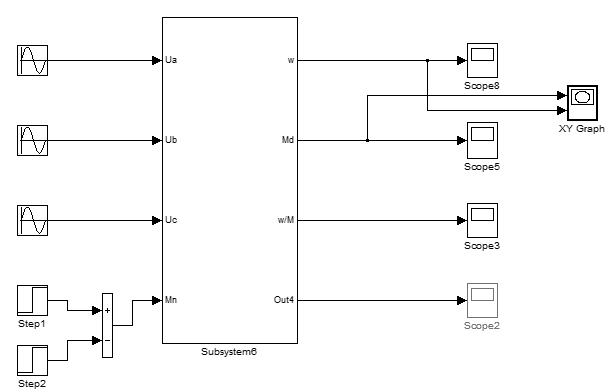
Рисунок 3.17 – Модель двигателя в трехфазной системе координат

Собственно, сам двигатель на рисунке 3.17 скрыт в виде маскируемой подсистемы Subsystem6, содержимое которой раскрывается на рисунке 3.18.

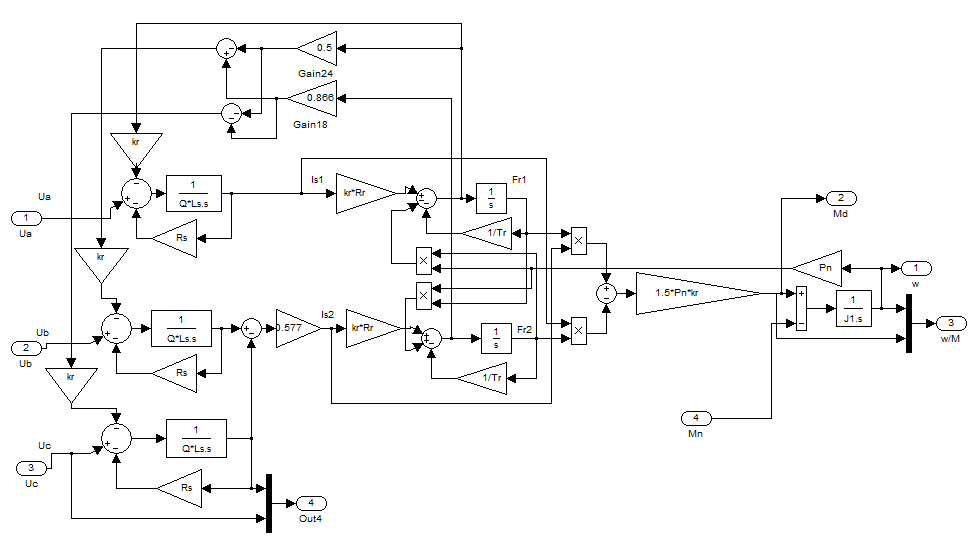
Рисунок 3.18 – Содержимое блока Subsystem6

Структура модели АД в трехфазных координатах в программе Matlab Simulink. Параметры схемы замещения, задаваемые в модели, приведены на рисунке 3.19. Результаты моделирования проиллюстрированы на рисунках 3.20 – 3.23.

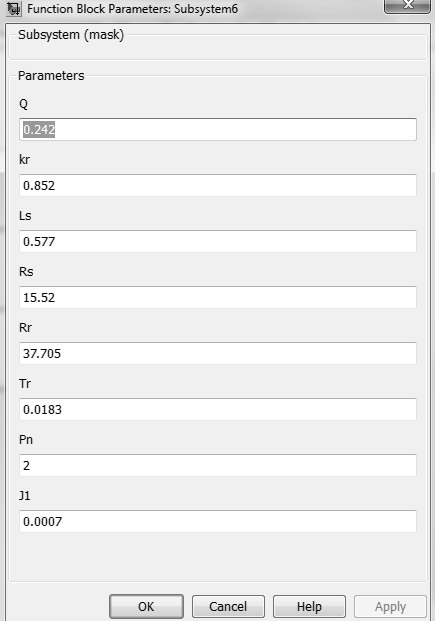
Рисунок 3.19 – Параметры схемы замещения асинхронного двигателя

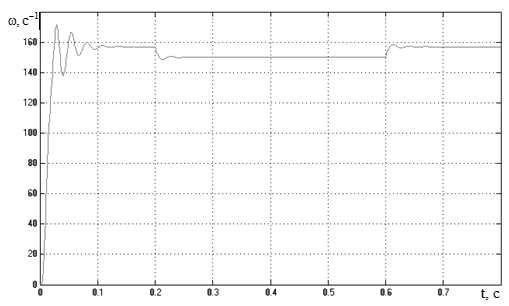
Рисунок 3.20 – График переходного процесса скорости АД,

полученный на трехфазной модели

Перерегулирование по скорости при пуске составляет

%. (3.79)

Перерегулирование по скорости при набросе нагрузки

%. (3.80)

При набросе нагрузки наблюдается статическая ошибка

%. (3.81)

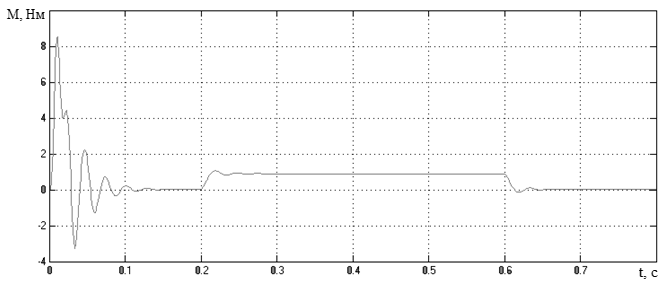
Рисунок 3.21 – Переходный процесс по моменту АД,

полученный на трехфазной модели

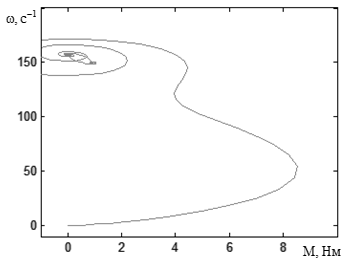
Рисунок 3.22 – Механическая характеристика асинхронного двигателя,

полученная в динамике на трехфазной модели

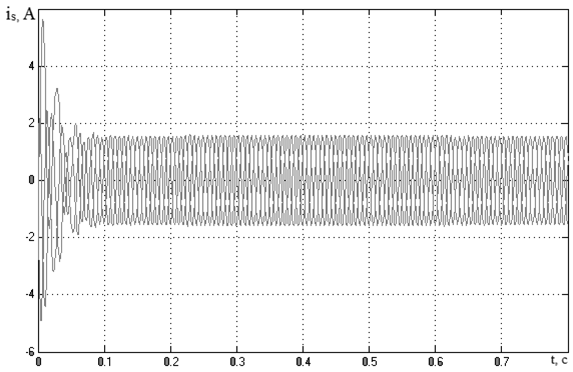
Рисунок 3.23 – Осциллограмма токов статора, полученная

на трехфазной модели

3.6 Исследование асинхронного двигателя на модели в SimPowerSystems

Пакет SimPowerSystems (в версии MATLAB 6.1 и ранее – Power System Blockset) содержит набор блоков для построения виртуальных моделей электротехнических устройств и устройств силовой электроники. Используя библиотеки Simulink и SimPowerSystems, а также применяя функции и команды MATLAB, пользователь может не только имитировать работу устройств во временной области, но и изучать их частотные свойства, оценивать динамические параметры и осуществлять гармонический анализ токов и напряжений.

Несомненным достоинством SimPowerSystems является то, что при моделировании сложных систем силовой электроники можно использовать функциональные (отражающие функции S-блоков), виртуальные (из элементов или SPS-блоков) и структурные модели. Так, силовой блок полупроводникового преобразователя электрической энергии строится на основе виртуальных блоков SimPowerSystems, а система управления – с помощью функциональных блоков Simulink, отражающих лишь алгоритм ее работы без электрической схемы. Такой подход значительно упрощает саму модель и, как следствие, повышает скорость ее работы. Важно заметить, что библиотека SimPowerSystems имеет относительно большее количество блоков, а также дает возможность создавать новые подсистемы из блоков, имеющихся в библиотеке, и привлекать функции MATLAB. Все это значительно расширяет возможности SimPowerSystems при использовании его совместно с Simulink.

Модель асинхронного двигателя в SimPowerSystems представлена на рисунке 3.24. Блок трехфазного напряжения, присутствующий на модели, раскрыт на рисунке 3.25. Параметры, задаваемые в блоке трехфазного напряжения, приведены на рисунке 3.26, а параметры двигателя, задаваемые в модели – на рисунке 3.27.

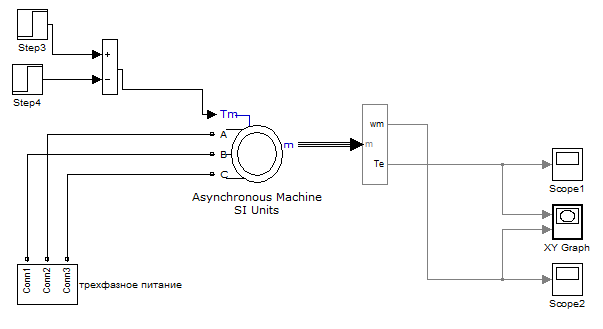
Рисунок 3.24 – Модель асинхронного двигателя в SimPowerSystems

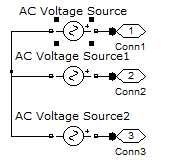
Рисунок 3.25 – Блок трехфазного напряжения

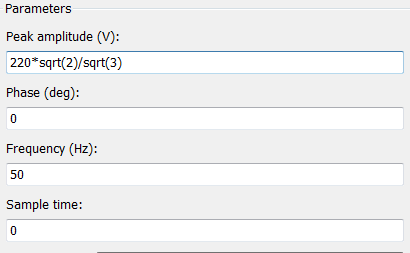
Рисунок 3.26 – Параметры блока трехфазного напряжения

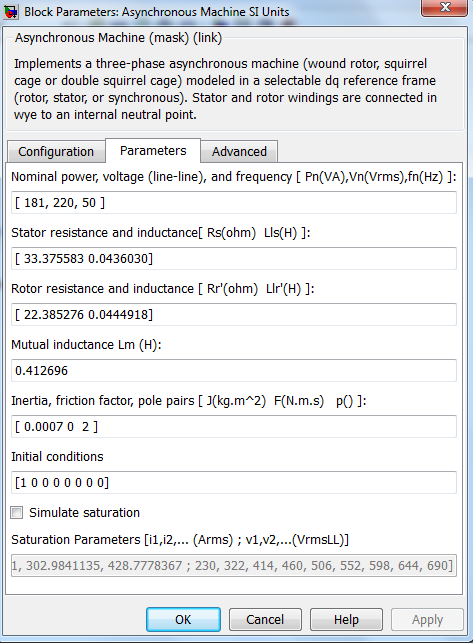
Рисунок 3.27 – Параметры двигателя, задаваемые в модели

Переходная функция по скорости, полученная на модели асинхронного двигателя в SimPowerSystems, представлена на рисунке 3.28, а по моменту – на рисунке 3.29. На рисунке 3.30 показана механическая характеристика асинхронного двигателя, полученная в динамике на модели в SimPowerSystems. На рисунке 3.31 приведены переходные функции по току статора.

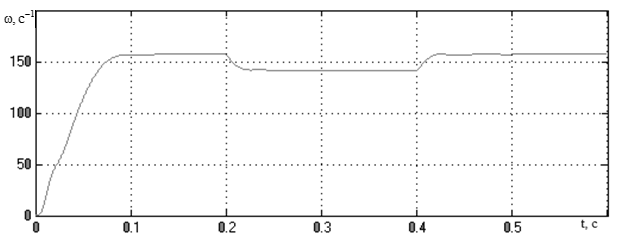
Рисунок 3.28 – График переходного процесса скорости АД,

полученная на модели асинхронного двигателя в SimPowerSystems

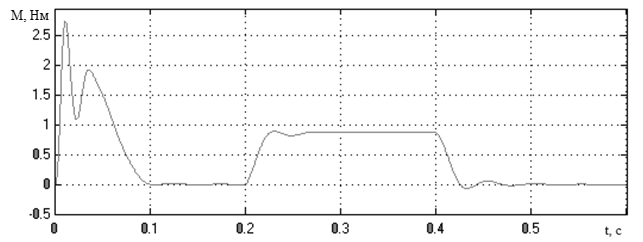
Рисунок 3.29 – График переходного процесса по моменту АД,

полученная на модели асинхронного двигателя в SimPowerSystems

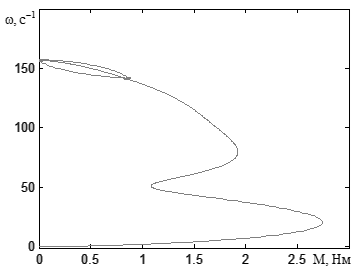
Рисунок 3.30 – Механическая характеристика асинхронного двигателя,

полученная в динамике модели в SimPowerSystems

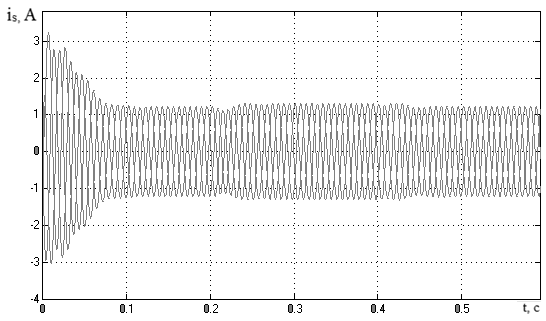
Рисунок 3.31 – Осциллограмма токов статора, полученная

на модели в SimPowerSystems

Проанализировав полученные переходные функции, можно сделать выводы, что результаты, получаемые на модели в двухфазной системе координат, неподвижной относительно статора, полностью совпадают с результатами моделирования в трехфазных координатах. Моделирование в SimPowerSystems существенно отличается. Этот факт связан с использованием в SimPowerSystems готовых блоков, в которых могут изменяться только некоторые из параметров.

3.7 Исследование двухмассового стенда с асинхронным двигателем на модели в двухфазной системе координат ( – )

Электромеханическая система с двухмассовой упругой механической частью представляет собой простейшую модель электропривода, наиболее удобную для изучения влияния упругих механических связей.

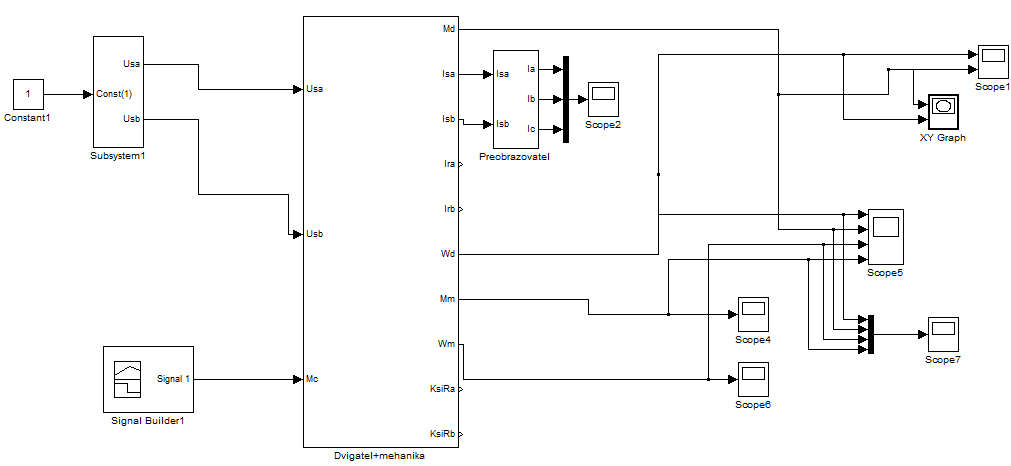
Рисунок 3.32 – Модель двухмассового стенда с асинхронным двигателем

в двухфазной системе координат ( – )

Собственно, сама двухмассовая модель приведена на рисунке 3.33 в виде маскируемой подсистемы Dvigatel+mehanika. Окно для ввода основных данных модели представлено на рисунке 3.34.

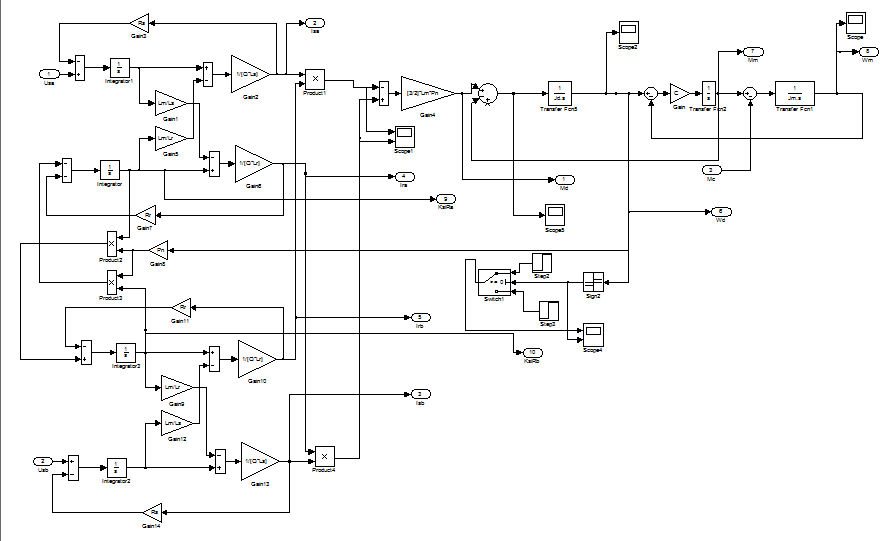
Рисунок 3.33 – Маскируемая подсистема Dvigatel+mehanika

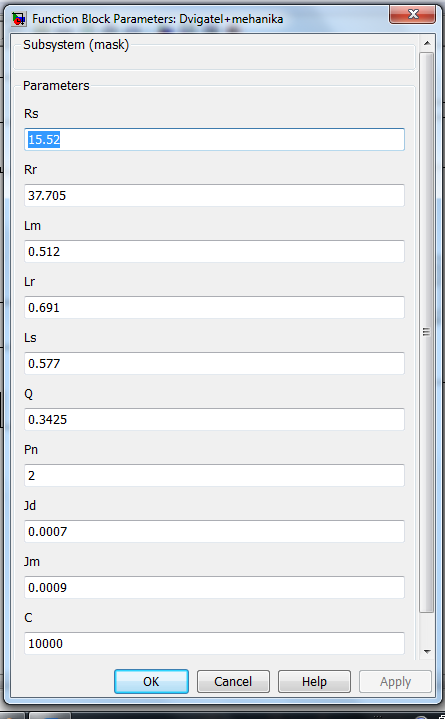
Рисунок 3.34 – Ввод основных данных

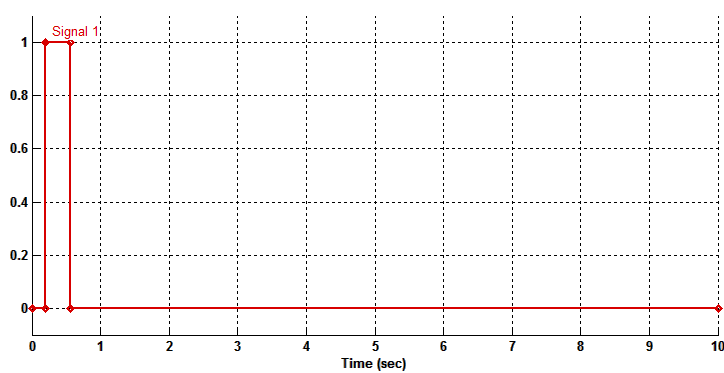
Рисунок 3.35 – Сигнал задания по моменту в относительных единицах

Переходные функции, полученные на модели двухмассового стенда в двухфазной системе координат ( – ) представлены на рисунках 3.36 – 3.38.

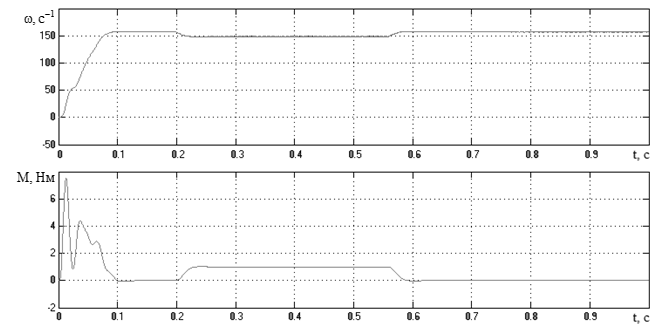
Рисунок 3.36 – Скорость и момент двигателя, полученные на модели

двухмассового стенда в двухфазной системе координат ( – )

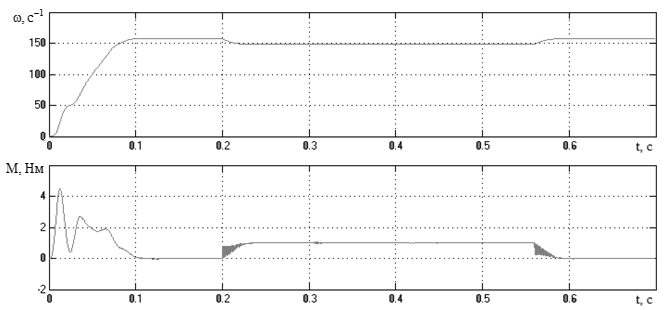
Рисунок 3.37 – Скорость и момент второй массы, полученные на модели

двухмассового стенда в двухфазной системе координат ( – )

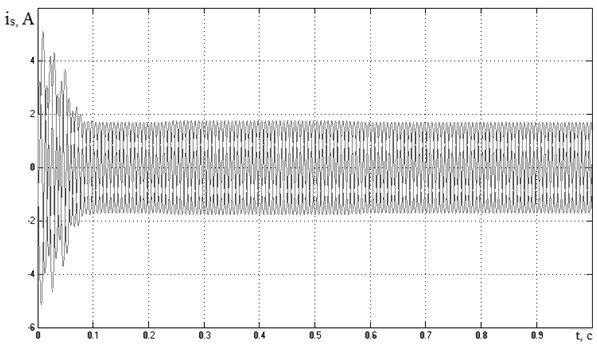
Рисунок 3.38 – Осциллограмма токов статора, полученная на модели

двухмассового стенда в двухфазной системе координат ( – )

Фазовый портрет, полученный на модели двухмассового стенда в двухфазной системе координат ( – ) представлен на рисунке 3.39.

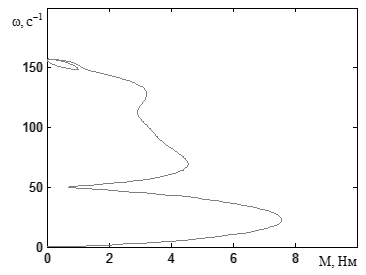
Рисунок 3.39 – Фазовый портрет, полученный на модели

двухмассового стенда в двухфазной системе координат ( – )

3.8 Исследование двухмассового стенда с асинхронным двигателем на модели в трехфазной системе координат

Модель двухмасоового стенда с асинхронным двигателем в трехфазной системе координат приведена на рисунке 3.40. Окно для ввода данных в модель представлено на рисунке 3.41.

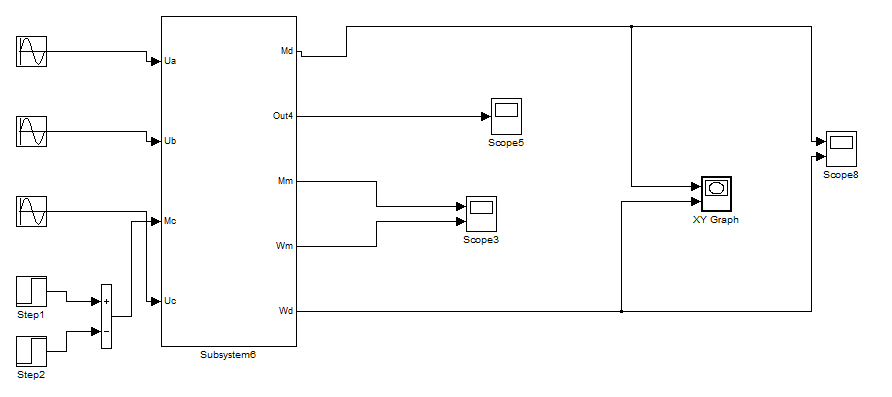
Рисунок 3.40 – Модель двухмасоового стенда с асинхронным двигателем в трехфазной системе координат

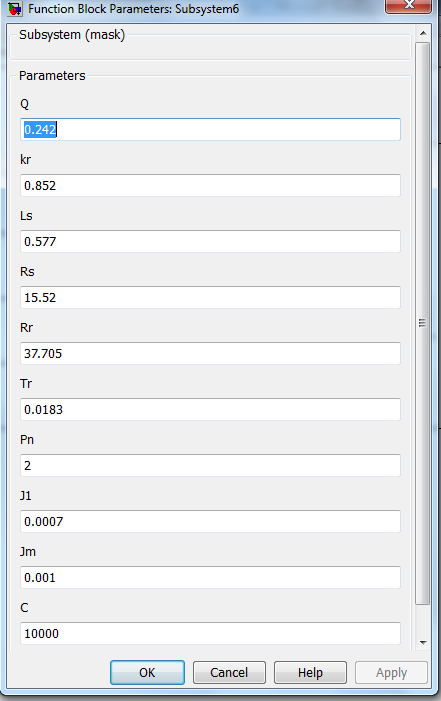
Рисунок 3.41 – Окно для ввода данных в модель

Содержимое подсистемы Subsystem6 приведено на рисунке 3.42.

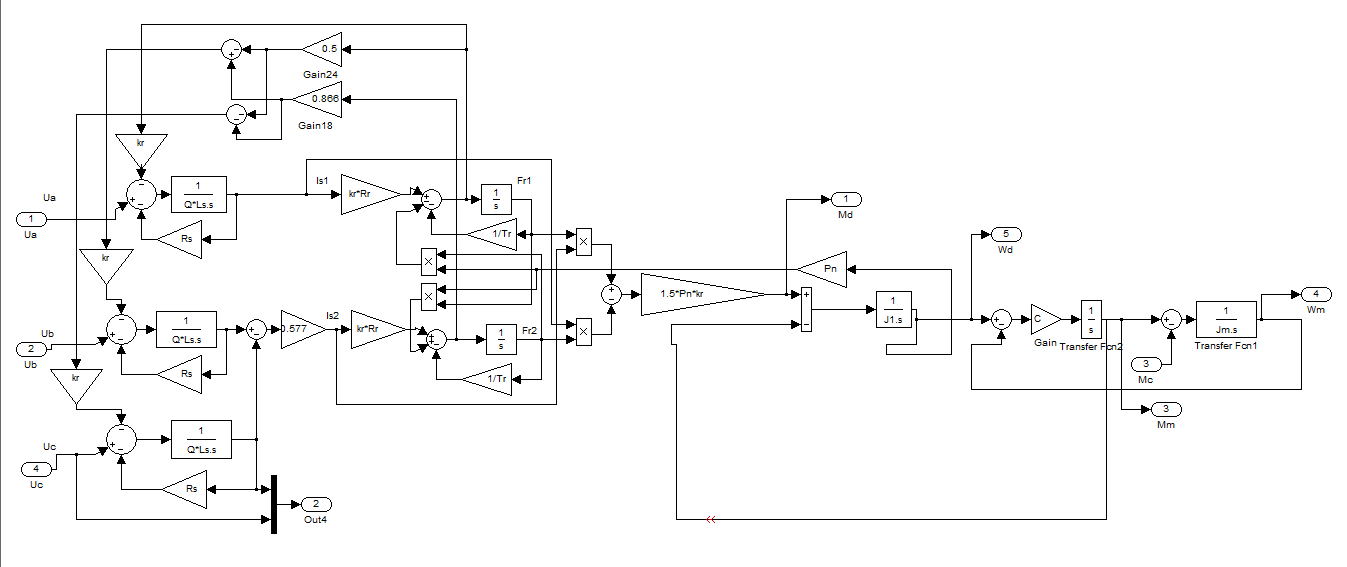
Рисунок 3.42 – Содержимое подсистемы Subsystem6

Переходные функции, полученные на модели двухмассового стенда в трехфазной системе координат, представлены на рисунках 3.43 – .

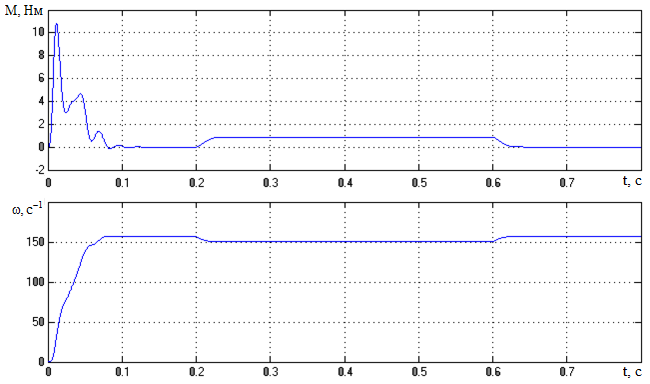
Рисунок 3.43 – Скорость и момент двигателя, полученные на модели

двухмассового стенда в трехфазной системе координат

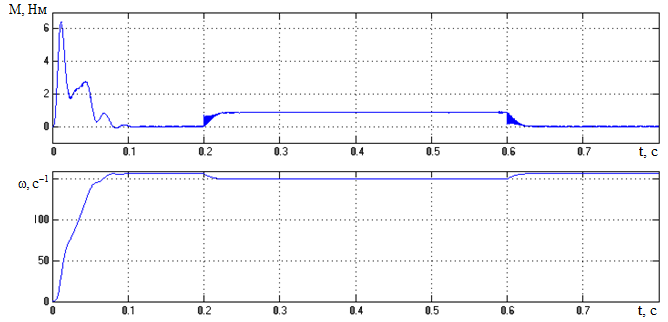
Рисунок 3.44 – Скорость и момент второй массы, полученные на модели

двухмассового стенда в трехфазной системе координат

Фазовый портрет, полученный на модели двухмассового стенда в трехфазной системе координат, представлен на рисунке 3.45.

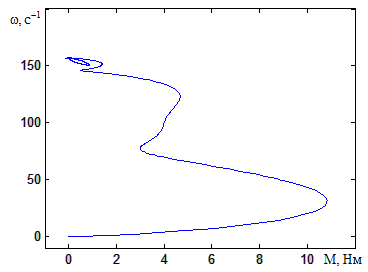
Рисунок 3.45 – Фазовый портрет, полученный на модели

двухмассового стенда в трехфазной системе координат

4 ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ ДВУХМАССОВОГО

ДИНАМИЧЕСКОГО СТЕНДА

4.1 Виды математических моделей и понятие адекватной модели

Математические модели могут быть детерменированными и стохастическими. Детерменированные модели – это модели, в которых установлено взаимно-однозначное соответствие между переменными описывающими объект или явления.

Такой подход основан на знании механизма функционирования объектов. Часто моделируемый объект сложен и расшифровка его механизма может оказаться очень трудоемкой и длинной во времени.

В этом случае поступают следующим образом: на оригинале проводят эксперименты, обрабатывают полученные результаты и, не вникая в механизм и теорию моделируемого объекта с помощью методов математической статистики и теории вероятности, устанавливают связи между переменными, описывающими объект.

В этом случае получают стохастическую модель. В стохастической модели связь между переменными носит случайный характер, иногда это бывает принципиально.

Воздействие огромного количества факторов, их сочетание приводит к случайному набору переменных описывающих объект или явление. По характеру режимов модель бывают статистическими и динамическими.

Статистическая модель включает описание связей между основными переменными моделируемого объекта в установившемся режиме без учета изменения параметров во времени.

В динамической модели описываются связи между основными переменными моделируемого объекта при переходе от одного режима к другому.

Модели бывают дискретными и непрерывными, а также смешанного типа. В непрерывных переменные принимают значения из некоторого промежутка, в дискретных переменные принимают изолированные значения.

Линейные модели – все функции и отношения, описывающие модель линейно зависят от переменных и нелинейные – в противном случае.

Требования, предъявляемые к моделям:

– универсальность – характеризует полноту отображения моделью изучаемых свойств реального объекта;

– адекватность – способность отражать нужные свойства объекта с погрешностью не выше заданной;

– точность – оценивается степенью совпадения значений характеристик реального объекта и значения этих характеристик полученных с помощью моделей;

– экономичность – определяется затратами ресурсов ЭВМ памяти и времени на ее реализацию и эксплуатацию.

Проверить адекватность модели – значит установить, насколько хорошо модель описывает реальные процессы, происходящие в системе, насколько качественно она будет прогнозировать развитие данных процессов.

Проверка адекватности проводится на основании некоторой экспериментальной информации, полученной на этапе функционирования системы или при проведении специального эксперимента, в ходе которого наблюдаются интересующие процессы.

Проверка адекватности заключается в доказательстве факта, что точность результатов, полученных по модели, будет не хуже точности расчетов, произведенных на основании экспериментальных данных.

4.2 Обработка экспериментальных данных. Общие выводы

При проведении эксперимента датчик скорости устанавливался на второй массе двухмассового стенда с асинхронным двигателем (таблица 4.1).

Таблица 4.1 – Экспериментальные данные

Момент времени, с	Значение скорости, полученное на модели, рад/c	Значение скорости, полученное в результате эксперимента, рад/c
Пуск	0	0	0
	0,02	76,5	73
	0,04	145,1	147
	0,06	159,4	161
	0,08	156,3	152
	0,1	156,2	148
	0,12	157,1	154
	0,14	157,3	156
	0,16	158	160
	0,18	157,1	154
Наброс нагрузки	0,2	156,9	157
	0,25	149,9	147
	0,3	150,1	150
	0,35	150,1	148
	0,4	150,1	149
	0,45	150,1	150
	0,5	150,1	147
	0,55	150,1	150
	0,6	150	148
Сброс нагрузки	0,62	156,9	159
	0,64	156,8	155
	0,66	156,7	156
	0,68	156,9	157
	0,7	156,9	155
	0,75	157	157
	0,8	157	156

Листинг программы, выполняющей обработку данных в Mathcad, представлен на рисунке 4.1.

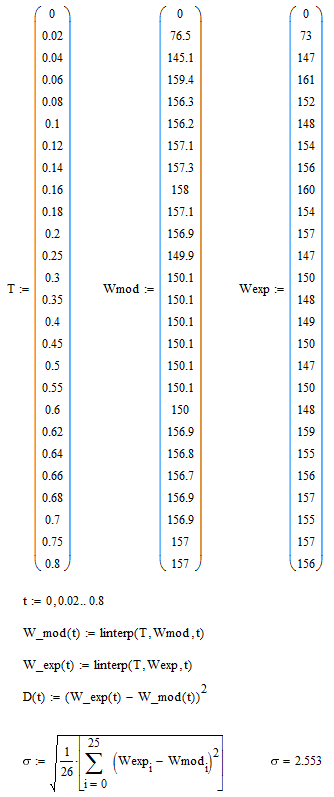
Рисунок 4.1 – Листинг программы в Mathcad

Как видим из рисунка 4.1, для обработки данных была применена линейная интерполяция, то есть интерполяция отрезками прямых, соединяющих между собой экспериментальные точки. Результаты обработки данных приведены на рисунках 4.2 и 4.3.

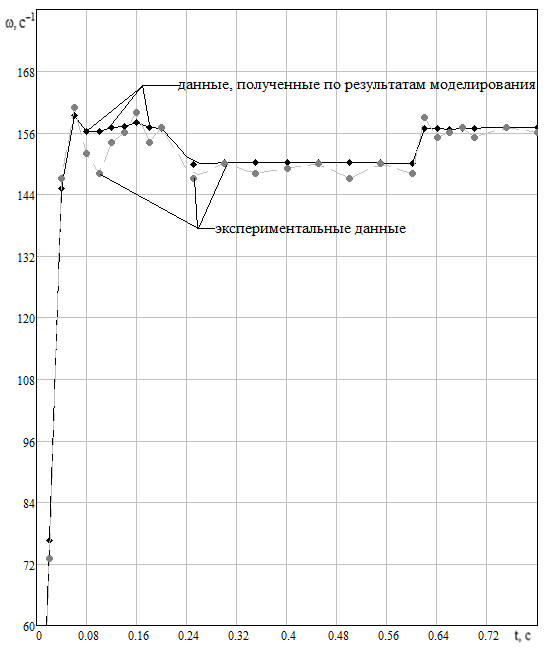
Рисунок 4.2 – Экспериментальные данные и данные, полученные на модели

после выполнения линейной интерполяции

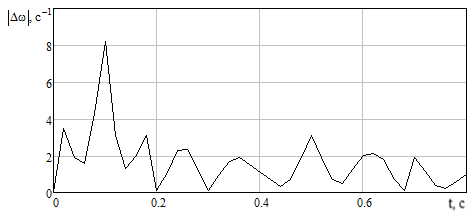
Рисунок 4.3 – Модуль отклонения между экспериментальными данными и данными, полученными на модели

Анализируя рисунки 4.2 и 4.3 приходим к выводу, что модель адекватно описывает поведение реального объекта – двухмассового стенда с асинхронным двигателем. Ошибкой эксперимента является шестая точка, в которой отклонение значительно превышает среднюю ошибку (в таблице 4.1 выделена курсивом).

Стандартное отклонение (иногда среднеквадратичное отклонение) – в теории вероятности и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно её математического ожидания. Измеряется в единицах измерения самой случайной величины. Равна корню квадратному из дисперсии случайной величины

, (4.1)

где – количество экспериментальных точек;

– i-ое значение, полученное на модели;

– i-ое значение, полученное в результате эксперимента.

График квадрата отклонения экспериментальных данных от данных, полученных на модели, представлен на рисунке 4.4. Исходя из рисунка 4.4 вычисляется среднеквадратическое отклонение для всех 26 экспериментальных точек (формула на рисунке 4.1).

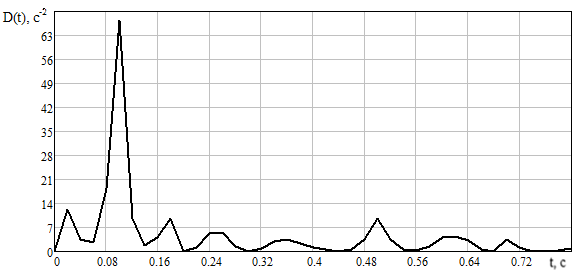
Рисунок 4.4 – Квадрат отклонения между экспериментальными данными и данными, полученными на модели

В результате проведенной обработки эксперимента установлено, что среднеквадратическое отклонение данных, полученных на модели, от экспериментальных данных составляет , а значит модель двухмассового стенда с асинхронным двигателем является адекватной. Уменьшить среднеквадратическое отклонение можно, выполнив повторные эксперименты, в частности, повторно измерив результаты в точке 6. Проблемным в данном смысле является также и тот факт, что процесс пуска очень быстротечен и для точного измерения скорости требуются датчики с достаточно высоким быстродействием.

5 ПРАКТИЧЕСКОЕ ДОПОЛНЕНИЕ РЕЗУЛЬТАТОВ ИССЛЕДОВАНИЯ

5.1 Техническая разработка лабораторного стенда на базе асинхронного

двигателя АИР56А4У3

5.1.1 Назначение установки АИР56А4У3

Установка по исследованию режимов работы трехфазной асинхронной машины АИР56А4У3 предназначена:

• для изучения конструкции и принципа работы трехфазного асинхронного двигателя;
• для исследования пуска трехфазного асинхронного двигателя;
• для изучения автотрансформаторного режима работы асинхронного

двигателя, а также для изучения режима работы АД с КЗ ротором и фазным ротором;

• для подтверждения теории и проверки на практике соотношения

f2=sf1 и E2s=sE1, для исследования механических характеристик трехфазной асинхронной машины;

• для изучения режима динамического торможения асинхронного

двигателя;

• для изучения частотного управления асинхронной машиной.

5.1.2 Внешний вид лабораторной установки

В ходе проведения исследований лабораторная установка была описана и сфотографирована (рисунок 5.1 и рисунок 5.2)

Рисунок 5.1 – Установка для пуска и исследования режимов работы АД

Рисунок 5.2 – Исследуемый асинхронный двигатель АИР56А4У3

5.1.3 Устройство и работа установки АИР56А4У3

Питание установки осуществляется от двух источников переменного тока трехфазного регулируемого (0-250) и однофазного (220 В). Установка представляет собой параллелепипед весом не более 10 кг. На внешних боковых панелях размещены клеммы подсоединения установки к источникам питания. Внутри блока размещены все функциональные части электрической схемы на основании блока установлен трехфазный АД типа АИР56А4У3. На вал двигателя насажен массивный диск для создания момента инерции. Второй конец вала выведен через заднюю панель наружу для измерения частоты вращения часовым тахометром. На боковых стенках параллелепипеда размещены кнопочные станции реверса и конденсаторного торможения. На лицевой панели размещены измерительные приборы, кнопки, тумблера. Блок управления позволяет осуществлять управление АД по определенной программе и исследовать различные режимы работы АД

Запускают установку в следующей последовательности

- присоединяют клеммы к трехфазному регулируемому источнику питания,

- запитывают цепь управления (однофазный источник 220В),

- замыкают тумблер и пакетный выключатель,

- выставляют напряжение.

- нажимают кнопку «Вперед» или «Назад» и Ад начинает вращаться с номинальной скоростью.

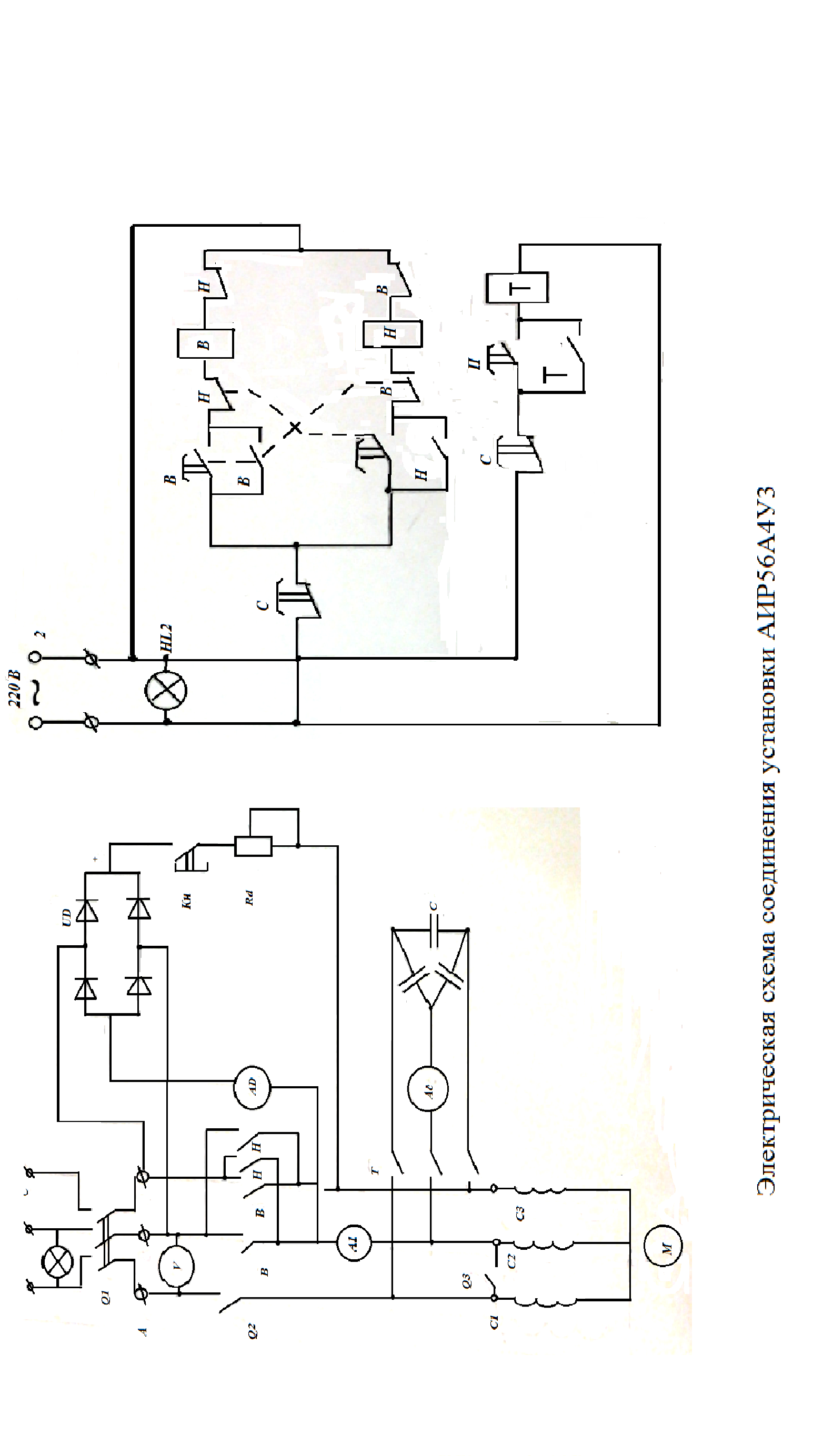
5.2 Охрана труда

5.2.1 Анализ опасных и вредных производственных факторов при работе на лабораторной установке АИР-56А4У3

Для исследования был взят асинхронный двигатель с короткозамкнутым ротором типа АИР-56А4У3, UH= 220 В, IH= 0.76 А, nH= 1350 об/мин, PH=120 Вт, H= 63%. Данная лабораторная установка позволяет рассмотреть режимы работы асинхронной машины – трансформаторный, АД с короткозамкнутым ротором, АД с фазным ротором, сравнить по эффективности релейно-контакторное управление и частотное векторное управление.

При работе на лабораторной установке АИР -56А4У3 на человека действует целый комплекс опасных и вредных производственных факторов (ОиВПФ).

К опасным физическим факторам относятся:

– движущиеся части установки;

– нагретые поверхности оборудования и механической нагрузки;

– высокое напряжение в силовой электрической сети и статическое электричество;

– электрические искры и дуги;

– возможность возникновения пожаров.

К вредным физическим факторам относятся:

– высокие влажность и скорость движения воздуха рабочей зоны, повышенная или пониженная температура;

– повышенные уровни излучений, шума и вибрации;

– повышенное содержание пыли в воздухе рабочей зоны;

– недостаточная освещенность, повышенная яркость света и пульсация светового потока.

Условия эксплуатации электроустановки следующие: помещение лаборатории достаточно пыльное с повышенным уровнем влажности. Тип помещения по опасности поражения электрическим током и по характеру среды относится к особо опасным помещениям.

Основные виды травм, которые можно получить при работе с электроустановкой:

– прикосновение к токоведущим частям под напряжением вследствие несоблюдения правил безопасности или дефектов конструкции;

– прикосновение к нетоковедущим частям, которые случайно оказались под напряжением (повреждение изоляции, замыкание проводов);

– ошибочная подача напряжения в установку, где работают люди;

Опасное воздействие на людей электрического тока проявляется в виде электротравм. Электрический ток, протекая через организм человека, вызывает четыре вида воздействия: термическое, электролитическое, механическое и биологическое.

Термическое действие проявляется в ожогах отдельных участков тела, нагреве до высоких температур внутренних тканей человека, что вызывает в них серьезные функциональные расстройства.

Электролитическое действие проявляется в разложении органических жидкостей, в том числе и крови, что вызывает значительные нарушения их физико-химического состава.

Механическое действие приводит к разрыву тканей и переломам костей.

Биологическое действие проявляется в раздражении и возбуждении живых тканей в организме, а также в нарушении внутренних биоэлектрических процессов, присущих нормально действующему организму; с биологической точки зрения исход поражения человека электрическим током может быть следствием тех физиологических реакций, которыми ткани отвечают на протекание через них электрического тока.

В физиологическом смысле действие электрического тока является экзогенным, то есть обусловленным факторами внешней среды. Реакции, происходящие при возникновении электрической цепи в теле человека, бывают различными, начиная от легкого раздражения и локальной судороги, кончая летальным исходом. Подобно любому другому физическому раздражителю электрический ток действует не только местно, повреждая ткани, но и рефлекторно (действия, вызванные реакцией нервной системы в ответ на раздражение электрическим током).

Данная электроустановка также является источником электромагнитных полей промышленной частоты, так как содержит токоведущие части. Длительное воздействие электромагнитного поля на организм человека может вызвать нарушение функционального состояния нервной и сердечно-сосудистой систем. Это выражается в повышенной утомляемости, снижении качества выполнения рабочих операций, болях в области сердца, изменении кровяного давления и пульса.

Анализ опасных и вредных производственных факторов показал необходимость разработки и проведения мероприятий по улучшению условий труда.

5.2.2 Разработка мероприятий для обеспечения безопасных условий труда

Основными требованиями безопасности, предъявляемыми к конструкции оборудования, машин и механизмов, являются:

- безопасность для здоровья и жизни человека на всех стадиях функционирования (монтаж, демонтаж, эксплуатация, ремонт, транспортировка, хранение),

- надежность эксплуатации,

- удобство эксплуатации,

- безопасность для окружающей среды (при эксплуатации не должно происходить загрязнение окружающей среды).

Основными нормативными документами, которые регламентируют безопасность работ с промышленным электрооборудованием являются:

– ГОСТ 12.1.002-84 «Электрические поля промышленной частоты. Допустимые уровни напряженности и требования к проведению контроля на рабочих местах»;

– ГОСТ 12.1.003-89 «Шум. Общие требования безопасности»;

– ГОСТ 12.2.003-91 «Оборудование производственное. Общие требования безопасности»;

– ГОСТ 23000-76 «Система «Человек – машина». Пульты управления. Общие эргономические требования»;

-НПАОП 40.1-1.01-97 «Правила безпечної експлуатації електроустановок»;

– СНиП III-84-76 «Система автоматизации».

Общие требования безопасности установлены ГОСТ 12.2.003-91 ССБТ «Оборудование производственное. Общие требования безопасности». Согласно этому стандарту безопасность производственного оборудования была обеспечена за счет следующих мероприятий:

• выбора принципа действия, схемы, элементов и соответствующих материалов;
• применением в конструкции оборудования средств защиты;
• применением в конструкции средств механизации, автоматизации и дистанционного управления;
• включением требований безопасности в техническую документацию по монтажу, эксплуатации и ремонту.

Общие требования безопасности к производственным процессам установлены ГОСТ 12.3.002-75 ССБТ «Процессы производственные. Общие требования безопасности». Согласно ГОСТу безопасность процессов была обеспечена выполнением следующих мероприятий:

• выбором технологического процесса и режима работы;
• рациональным распределением функций между человеком и оборудованием;
• обучением работающих;
• включением требований безопасности в нормативно-технические документы.

При выборе технологического процесса и режима работы были учтены:

• опасные и вредные производственные факторы, возможность их устранения и защиты от них;
  • возможности механизации и автоматизации установки, применения дистанционного управления;
  • возможность введения системы контроля и управления процессами, которые обеспечивают защиту работающих и аварийное отключение оборудования;
  • своевременное получение информации о возникновении ОиВПФ при выполнении отдельных технологических операций;
  • обеспечение пожарной и взрывной безопасности процесса;
  • выполнение требований охраны окружающей среды.

Специфика организации рабочего места зависит от характера решаемых задач и особенностей предметно-пространственного окружения. Она определяет типы средств управления производственным процессом, отображения информации и способы их размещения, рабочее положение тела, вид спецодежды и средства индивидуальной защиты, возможность пауз для отдыха, наличие пространства для наладки, ремонта оборудования, организационной и технической оснастки

Организационная оснастка обеспечивает эффективную организацию труда путем создания удобства и безопасности в эксплуатации и обслуживании основного производственного оборудования.

В состав организационной оснастки входят: рабочая мебель, устройства и приспособления для хранения и транспортирования предметов и продуктов труда, средства сигнализации и связи, средства освещения, тара, планшеты, аптечка, противопожарные средства, СИЗ, приспособления для ухода за машиной и уборки рабочего места.

К факторам, определяющим организацию рабочего места, относятся положение тела, рабочая поза, рабочие движения, максимальный темп движений, зоны деятельности.

Положение тела прежде всего влияет на пространственную компоновку рабочего места. Рабочее место было спроектировано так, что выполнение трудовых действий осуществляется в наиболее рациональных рабочих положениях. При выборе положения работающего учитывались:

• величина физической нагрузки при работе;
• размеры рабочей зоны и необходимость передвижения в ней;
• особенности технологического процесса, в том числе требуемую точность действий, характер чередования по времени пассивного наблюдения и физических действий, необходимость ведения записей и другие факторы.

Было выбрано рациональное рабочее положение, которое обеспечивает создание наибольшего удобства для работающего и наименьшего его утомления.

Наиболее часто используется рабочие положения «сидя» и «стоя». Размерные характеристики и требования к организации таких рабочих мест регламентируются ГОСТ 12.2.032-78 ССБТ «Рабочее место при выполнении работ сидя. Общие эргономические требования» и ГОСТ 12.2.033-78 ССБТ «Рабочее место при выполнении работ стоя. Общие эргономические требования».

Пульт управления является основным функциональным элементом рабочих мест с автоматизированным управлением, а также рабочих мест смешанного типа с наличием автоматизированного элемента.

Общие эргономические требования к пультам управления установлены ГОСТ 23000-78. В состав пульта управления входит: панель управления, кресло, органы управления и средства отображения информации. Элементы пульта управления удовлетворяют нормативным требованиям. При взаимном расположении элементов рабочего места оператора были учтены требования (ГОСТ 22269-76):

• рабочую позу человека-оператора;
• пространство для размещения человека-оператора;
• возможность обзора элементов рабочего места;
• возможность осуществления всех необходимых движений и перемещений для эксплуатации и технического обслуживания оборудования;
• возможность обеспечения оптимального режима труда и отдыха.

Все мероприятия по профилактике электротравматиза можно разделить на организационные и технические.

К организационным мерам относятся: нормативные документы, разделение сетей и помещений по степени опасности поражения электрическим током, разделение персонала на квалификационные группы, обучение, инструктаж, соответствующая организация работ, медосмотры и т.п.

Основные нормативные документы по электробезопасности:

• ГОСТ 12.1.019-79 «Электробезопасность. Общие требования»;
• ГОСТ 12.1.009-76 «Электробезопасность. Общие требования»;
• ГОСТ 12.1.030-87 «Электробезопасность. Защитное заземление, зануление»;
• ГОСТ 12.1.038-82 «Электробезопасность. Предельно допустимые уровни напряжений прикосновения и токов»;
• НПАОП 40.1-1.07-01 «Правила експлуатації електрозахисних засобів»;
• НПАОП 40.1-1.01-97 «Правила безпечної експлуатації електроустановок»;
• НПАОП 40.1-1.21-98 «Правила безпечної експлуатації електроустановок споживачів».

Технические мероприятия по профилактике электротравматиза можно разделить на три группы:

• мероприятия, осуществляемые при нормальном режиме работы электроустановок;
• мероприятия, осуществляемые при аварийном режиме работы электроустановок;
• применение системы электрозащитных средств.

Для обеспечения защиты работающих на установке АК-51 от поражения электрическим током были проведены следующие мероприятия в соответствии с требованиями ГОСТ 12.1.019-79 ССБТ «Электробезопасность. Общие требования»:

– заземление и зануление металлических конструкций;

– применение безопасного напряжения (местное освещение не должно иметь напряжение более 36 В);

– недоступность токоведущих частей;

– расчет изоляции проводов по высшему напряжению;

– маркировка или цветная изоляция монтажных проводов;

– исключение самопроизвольного включения устройств электрической схемы;

– применение индивидуальных средств защиты и др.

Изоляция предотвращает протекание через нее токов благодаря большому сопротивлению.

C целью обеспечения надежной работы изоляции проводятся профилактические мероприятия. B первую очередь исключаются механические повреждения, увлажнение, химическое влияние, запыленность.

Ho даже при нормальных условиях изоляция постоянно теряет свои первоначальные свойства, стареет. Поэтому осуществляется периодический и непрерывный контроль изоляции. В данной электроустановке используют двойную изоляцию.

Так как электроустановка напряжением до 1000 B, то при монтаже были применены изолированные провода, которые обеспечивают достаточную защиту от поражения при прикосновении к ним.

Для повышения безопасности электроустановки используются сплошные стационарные ограждающие устройства.

Для предотвращения неправильных включений имеется блокировка.

Одним из основных мероприятий по обеспечению электробезопасности является организация защитного заземления.

Заземлены все металлические элементы электроустановки, не несущие ток. Это необходимо на случай аварии, при которой шкаф, кожух, трубы, узел окажутся под напряжением относительно земли. Прикосновение к такому предмету человека вызовет поражение его током. Станина двигателя соединена луженым винтом со стальной полоской, входящей в систему заземления лаборатории.

При перегрузке электродвигателя могут сгореть его обмотки, что выведет двигатель из строя, и может привести к поражению оператора током. Поэтому при появлении перегрузок необходимо срочное отключение двигателя от сети. Простейшими аппаратами, обеспечивающими такое отключение, являются плавкие предохранители. Для этой же цели применяют тепловое реле и реле тока. Чрезвычайно важным является обеспечение так называемой нулевой защиты, т.е. защиты от самопроизвольного пуска двигателя при восстановлении напряжения после аварийного понижения его до нуля или ненормально низких значений.

Мероприятия, обеспечивающие пожаробезопасность и взрывобезопасность выполнены в соответствии с ГОСТ 12.1.004-91 «Пожарная безопасность. Общие требования», ГОСТ 12.1.033-81 «Пожарная безопасность. Термины и определения», ГОСТ 12.1.044-89 «Пожароопасность веществ и материалов. Номенклатура показателей и методы их определения»,

ГОСТ 12.1.010-76 «Взрывобезопасность. Общие требования», ОНТП 24-86 «Определение категорий помещений и зданий по взрывопожарной и пожарной опасности», СНіП 2.01.02-85 «Противопожарные нормы проектирования зданий и сооружений».

Причинами, которые могут вызвать пожар в электроустановки, являются короткие замыкания, перегрузки, переходные сопротивления.

При проектировании электрических установок прежде всего необходимо, чтобы все оборудование по своему исполнению соответствовало характеру окружающей среды и технологическому процессу

Существуют технические и организационные мероприятия для обеспечения пожаробезопасности. К техническим мероприятиям относятся: повышение огнестойкости зданий и сооружений облицовкой или оштукатуриванием металлических конструкций. Преимуществом пользуются облицовочные материалы, обладающие минимальной массой и минимальным коэффициентом температуропроводности.

Условия развития пожара в зданиях и сооружениях во многом определяются способностью отдельных строительных элементов сопротивляться воздействию огня, т.е. их огнестойкостью.

Огнестойкость – способность строительных элементов и конструкций сохранять несущую способность, а также сопротивляться нагреву до критических температур, образованию сквозных отверствий и распространению огня.

Для обеспечения пожарной безопасности применяют автоматические средства обнаружения пожаров с оповещением дежурного персонала о пожаре и месте его возникновения. При возникновении пожара установку необходимо немедленно выключить и действовать согласно, установленных правил.

Инструктаж по пожарной безопасности проводит преподаватель для студентов с дальнейшей росписью их в журнале по технике безопасности. Студенты, не прошедшие инструктаж или не расписавшиеся в журнале к занятиям не допускаются.

5.2.3 Расчет защитного заземления

Особая опасность поражения человека в процессе эксплуатации электрооборудования возникает при появлении напряжения на нормально нетоковедущих частях, например, на корпусе. В этих случаях заземление является одной из основных мер профилактики электротравматизма.

Согласно Правилам устройства электроустановок заземление или зануление следует выполнять:

– при напряжении 380 В и выше переменного тока и 440 В и выше постоянного тока – во всех электроустановках;

– при номинальных напряжениях выше 42 В, но ниже 380 В переменного тока и выше 110 В, но ниже 440 В постоянного тока в помещениях с повышенной опасностью, особо опасных и в наружных установках.

Назначение защитного заземления - устранение опасности поражения людей электрическим током при появлении напряжения на конструктивных частях электрооборудования, то есть при замыкании на корпус. Принцип действия защитного заземления - снижение до безопасных значений напряжений прикосновения и шага, обусловленных замыканием на корпус. Это достигается снижением потенциала заземленного оборудования, а также выравниванием потенциалов за счет поднимания потенциала основы, на которой стоит человек, к потенциалу, близкому по значению потенциалу заземленного оборудования.

Конечной целью расчета защитного заземления является определение сопротивления растеканию тока всего заземляющего устройства.

Рассчитывается защитное заземляющее устройство, выполненное из труб, забитых с заглублением h, расположенных по контуру сооружения..

Параметры заземляющей установки:

• длина трубы l=2,8 м;
• диаметр трубы d=0,05 м;
• расстояние между трубами a=2,5 м;
• величина заглубления h=0,6м;
• ширина полосы b=0,06 м;
• тип грунта – сухоглинок;
• влажность грунта – низкая.
• удельное сопротивление чернозема =100 Омм;
• климатический коэффициент =1,4.

Определяем расчетное сопротивление:

Омм (5.1)

Определяем сопротивление растеканию тока одиночного заземлителя по формуле:

(5.2)

где t – расстояние от поверхности земли до середины заземлителя

м. (5.3)

Определяем условное (приближенное) количество труб:

(5.4)

где Ом – согласно ПУЭ.

По величине, отношению определяем

коэффициент использования=0,53.

(5.5)

Рассчитываем длину соединительной полосы по формуле:

м (5.6)

где - расстояние между трубами; - количество труб.

Сопротивление растеканию тока полосы определяем по формуле:

(5.7)

Вычисляем сопротивление растеканию тока всего заземляющего устройства:

(5.8)

Ом. (5.9)

Полученное значение сопротивления растеканию тока всего заземляющего устройства меньше требуемого (нормируемого) значения, следовательно, заземляющее устройство рассчитано правильно.

Разработанные мероприятия по улучшению условий труда на рассматриваемых рабочих местах обеспечивают выполнение требований к воздуху рабочей зоны, уровню шума, освещению, электробезопасности, пожарной безопасности, организации рабочего места в соответствии с нормативными требованиями.

5.3 Экономическое обоснование

5.3 .1 Сущность и актуальность созданной установки АИР-56А4У3

Лабораторная установка АИР-56А4У3 позволяет рассмотреть не только различные режимы работы асинхронной машины – трансформаторный, АД с к.з. ротором, АД с фазным ротором, но также продемонстрировать эффективность частотного управления по сравнению с релейно-контакторным.

В данной установке объектом исследования является асинхронный двигатель трехфазного тока АИР-56А4У3. Одним из главных преимуществ асинхронных двигателей является возможность осуществлять регулировку скорости достаточно широких пределах и для этого чаще всего достаточно одного датчика. Это очень важно потому, что в некоторых случаях датчики могут стоить дороже самого двигателя.

Частотное управление асинхронным двигателем, позволяет:

– уменьшить пусковые токи;

– возможность работы в широком диапазоне скоростей;

– повысить точность управления;

– уменьшить потребляемую мощность.

5.3.2 Анализ предлагаемой лабораторной установки АИР-56А4У3

Проектируемая система управления имеет следующие особенности:

– предполагает современное микропроцессорное управление;

– позволяет уменьшить время на проведения различных операций по сравнению с более простыми системами управления;

– позволяет подготовить специалистов более высокого квалификационного уровня;

– регулирование скорости от нуля до номинальной и выше номинальной;

– плавный разгон и торможение;

– ограничение тока на уровне номинального в пусковых, рабочих и аварийных режимах;

– увеличение срока службы механической и электрической частей оборудования;

– высвобождается некоторое оборудование;

– монтаж частотного преобразователя возможен в стандартной ячейке распредустройства на месте высвобождаемого оборудования.

5.3.3 Расчет капитальных затрат на создание установки АИР-56А4У3

В состав капитальных затрат по созданию лабораторного стенда входят: