КІНЕТОСТАТИЧНИЙ РОЗРАХУНОК СХЕМИ ЗБАЛАНСОВАНОГО МАНІПУЛЯТОРА
. КІНЕТОСТАТИЧНИЙ РОЗРАХУНОК СХЕМИ ЗБАЛАНСОВАНОГО МАНІПУЛЯТОРА.
Зупинимось на особливостях кінетостатичного розрахунку схеми маніпулятора за умови вертикального підйому вантажу (рух від гідроприводу
отримує точка А , Точку В вважаємо нерухомою).
Вважаємо заданими :
mв – маса вантажу;
mі - маси ланок механізму;
Isi - моменти інерції ланок механізму відносно осей, що проходять через центри мас і перпендикулярних до площини руху.
Кінетостатичне дослідження виконуємо по групах Ассура, розпочинаючи з найбільш віддаленої від початкових ланок.
Виокремлюємо групу 4-5 (рис. 5.) і навантажуємо її зовнішніми силами, і силами інерції. Складемо рівняння рівноваги групи 4-5 у векторному вигляді
Складемо векторне рівняння рівноваги для групи 4-5:
У наведеному рівнянні 4 невідомих величини , тому, попередньо визначимо тангенціальні складові. Складемо умову рівноваги однієї ланки 4 у вигляді суми моментів відносно точки F.
;
,
де плечі сил, що діють на ланку 4 відносно точки F ;
Мі4 – момент від сил інерції, що діє на ланку 4;
Мі4 = Is4 *4 ;
Fi4, Fiв – сили інерції від ланки 4 і вантажу;
Fi4 = m4 * as4 ; Fiв = mв * aС ;
G4, GВ - вага ланки 4 і вантажу;
- масштабний коефіцієнт кінематичної схеми механізму,
З рівняння (28) визначаємо:
. (29)
Складаємо рівняння рівноваги ланки 5 у вигляді суми моментів відносно точки Е.
, (30)
звідки тангенціальна складова
. (31)
Якщо після обчислень величини чи матимуть знак (-), в такому випадку відповідний вектор на схемі (рис. 6) необхідно повернути в протилежному напрямку.
Далі відповідно рівнянню (27) в масштабі будуємо силовий багатокутник:
. (32)
В рівнянні (1) невідомими є два вектори i , їм відповідають векторні відрізки і , тому побудову розпочинаємо з векторного відрізка , тобто з точки а. Після закінчення побудови відомих векторів, з точки к проводимо пряму паралельну BF , що відповідає лінії дії нормальної складової , а з точки а - пряму паралельну DC, що є лінією дії . На перетині цих прямих маємо точку m. Тоді нормальні складові реакцій ; .
Враховуючи, що і , отримуємо результуючі реакції ; .
Розглядаємо наступну групу Ассура (ланки 3-6).
Аналогічно, як і для попередньої групи Ассура запишемо умову рівноваги структурної групи у векторному вигляді:
(33)
Для визначення запишемо умову рівноваги ланки AD у вигляді суми моментів відносно точки Е
.
(34)
(35)
Аналогічно для визначення розглянемо рівновагу ланки BE.
(36)
(37)
де - плечі відповідних сил відносно точки Е.
Якщо після розрахунків виявиться, що чи мають знак (-), напрями їх векторів необхідно змінити на протилежні.
Будуємо силовий багатокутник (рис. 7) відповідно рівнянню (33):
(38)
Побудову розпочинаємо з вектора , тобто з точки n. Аналогічно попередній групі, з точки f проводимо пряму паралельну ланці BE, а з точки n - пряму паралельну до ланки AD.
Тоді маємо ; .
Враховуючи, що і ,
Результуючі реакції ;
Визначимо зусилля, що діє від ланки 3 на гідроциліндр 1.
З цією метою знайдемо вектор сили , який отримуємо з векторного багатокутника (рис. 8). Відповідно 3-му закону Ньютона , тоді вектор (zo) в масштабі , спрямований в протилежному напрямку і буде зусиллям . Беремо до уваги те, що шток гідроциліндра 1 рухається у вертикальному напрямку вздовж осі у . Тоді зусилля , що діє на шток гідроциліндра 1 визначаємо відповідно до розрахункової схеми (рис. 8)
R1 = R31*cos. (39)
Для визначення сили, що діє на гідроциліндр 2 в точці В, (рис. 1), знайдемо результуюче зусилля від ланок 5,6 відповідно векторного рівняння:
(40)
Враховуємо ту обставину, що шток гідроциліндра 2 рухається горизонтально (вздовж осі абсцис), а результуюче зусилля від ланок 5, 6 спрямоване до осі ах під деяким кутом . Тоді, зусилля на шток циліндра без врахування тертя визначаємо за формулою
. (41)
Аналогічно виконують розрахунок за умови переміщення повзуна 2.
PAGE 7
а
b
k
m
c
d
e
g
h
Рис.6. Силовий багатокутник для групи 4-5
EMBED Equation.DSMT4 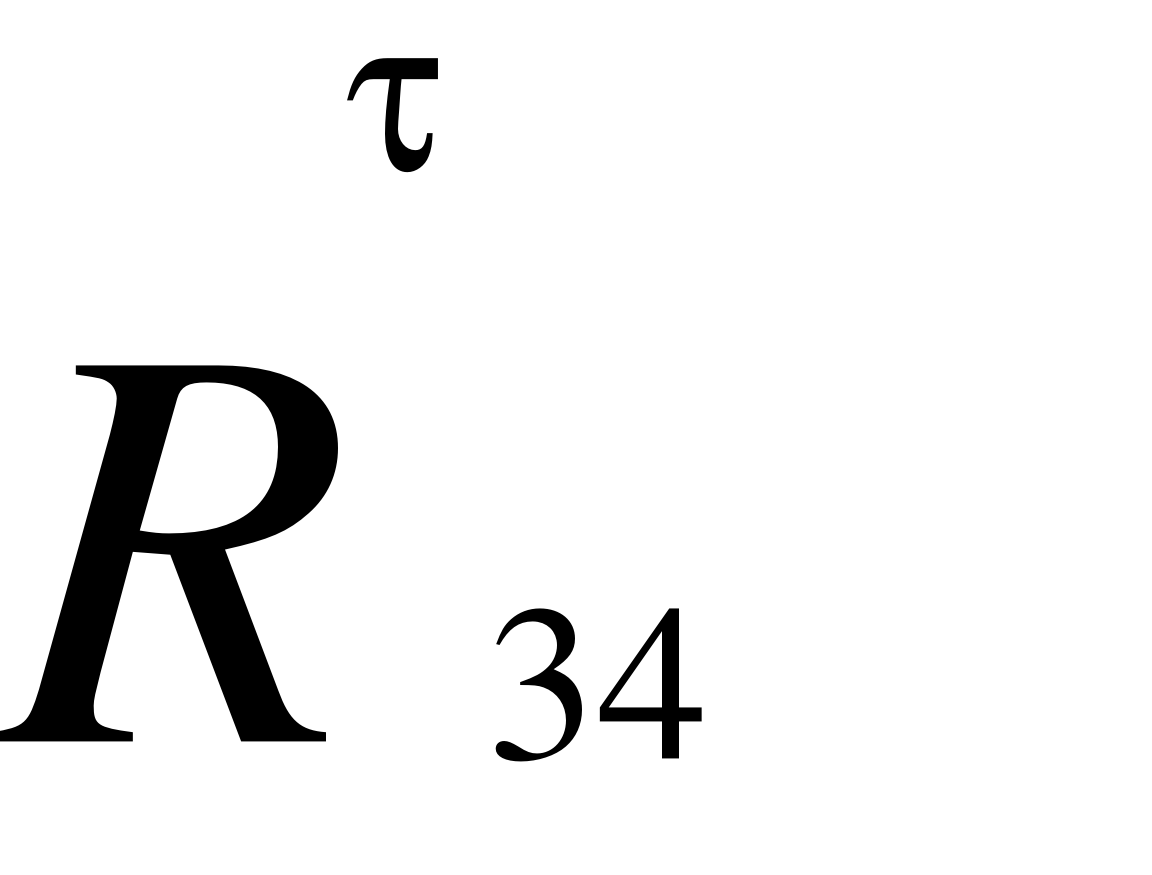
EMBED Equation.DSMT4 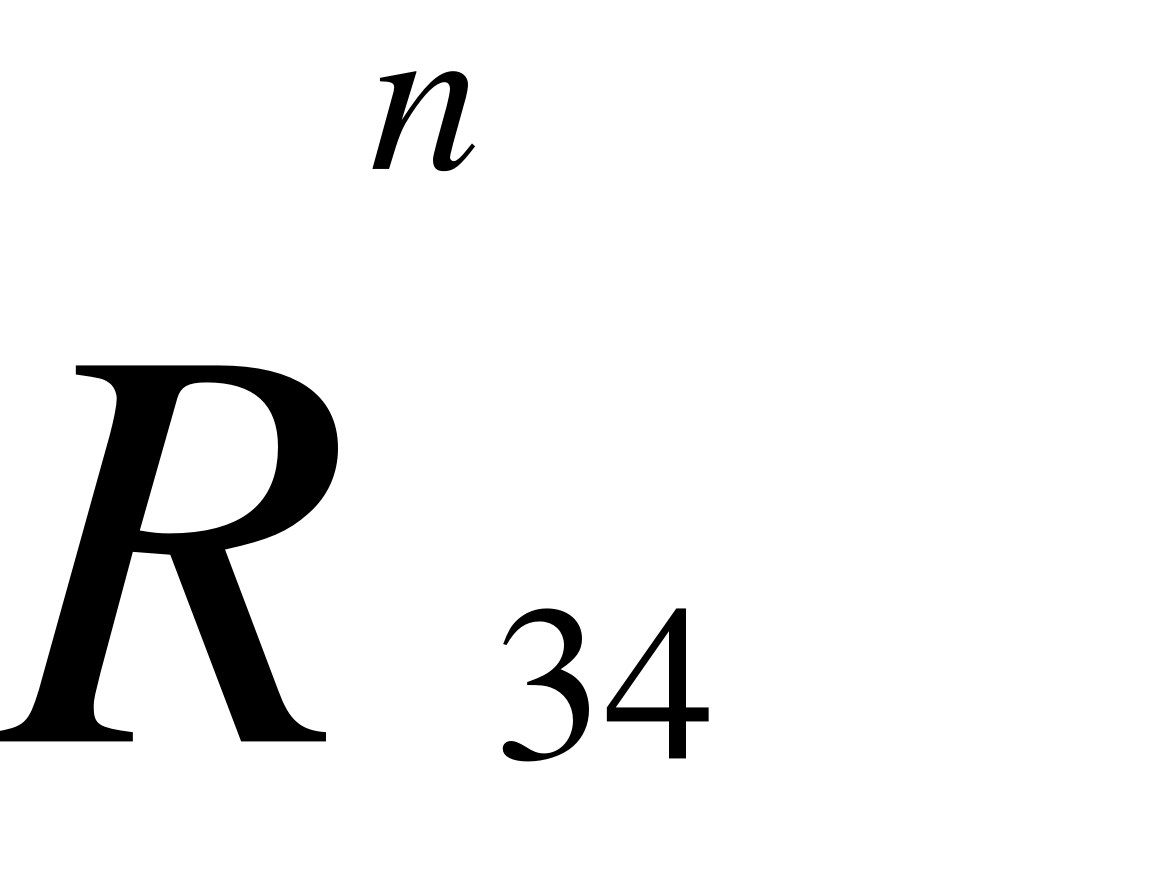
DC
BF
EMBED Equation.DSMT4 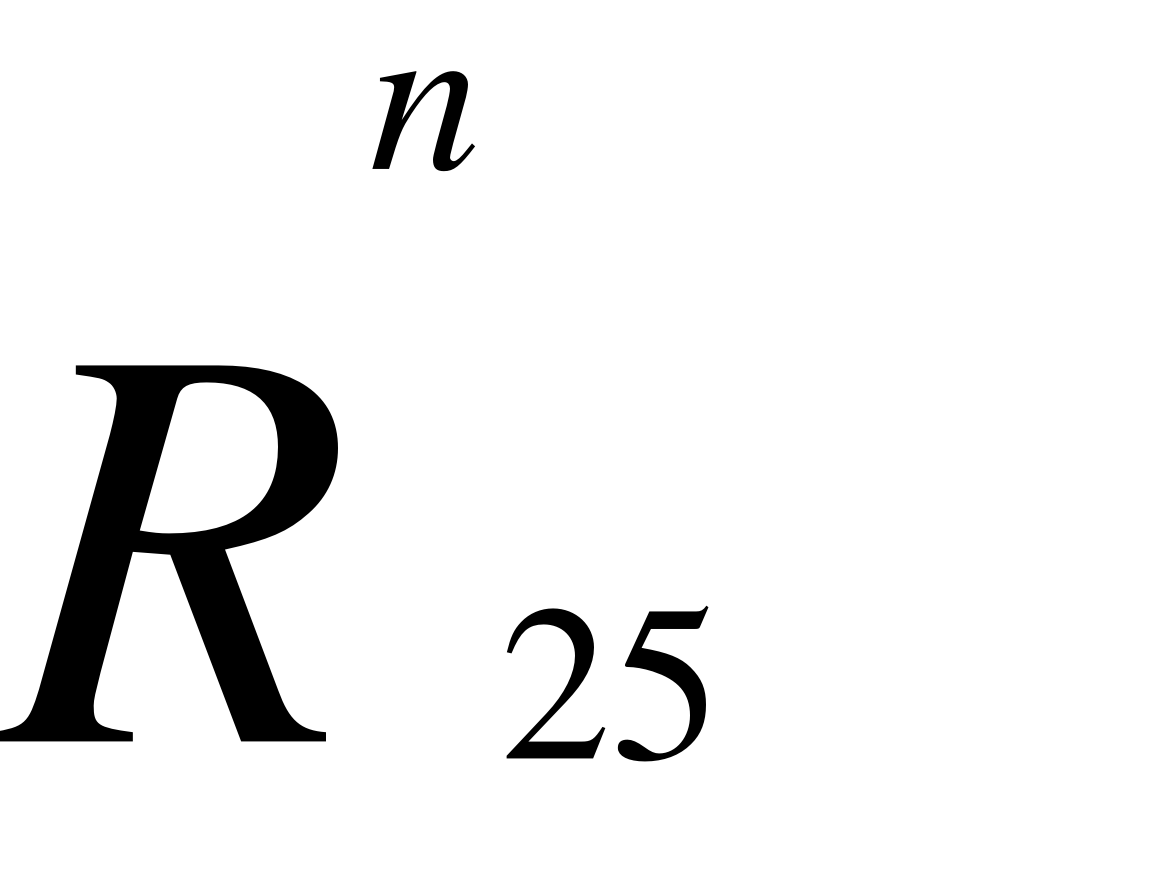
EMBED Equation.DSMT4 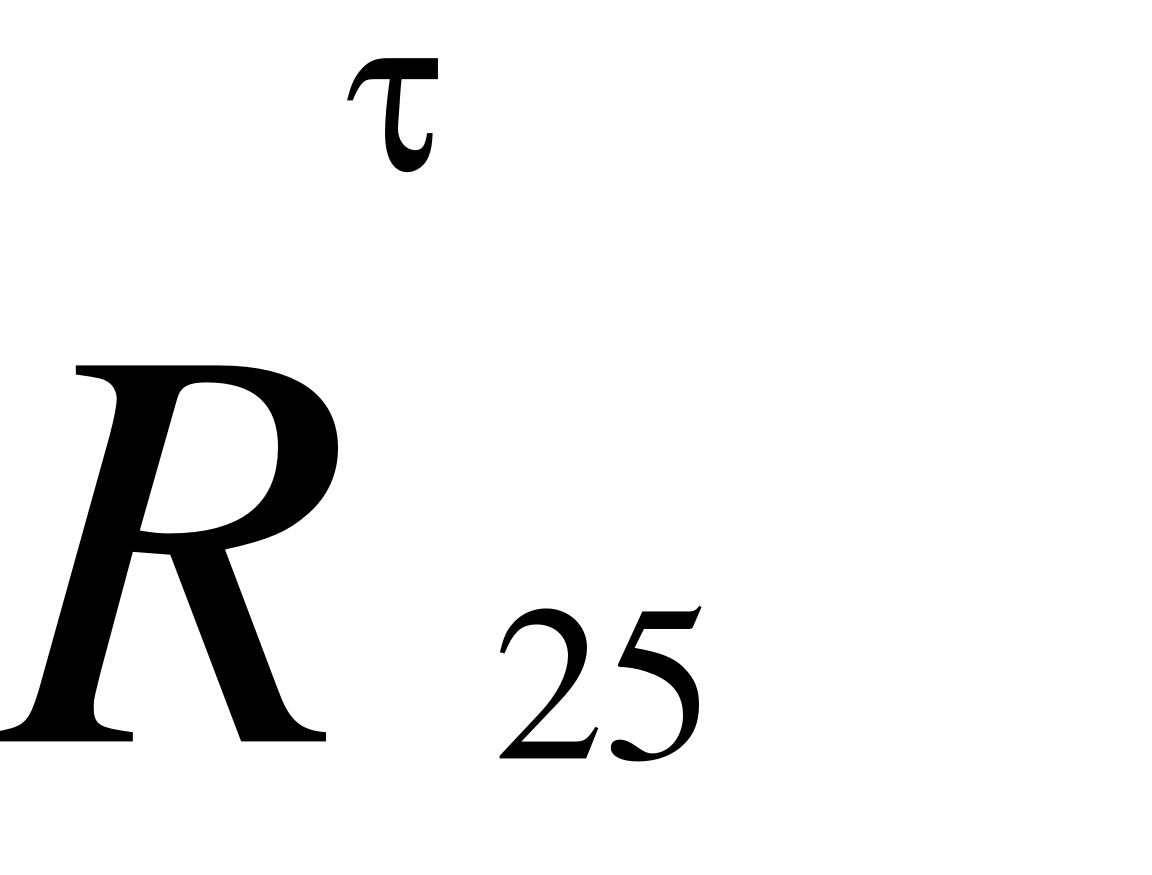
EMBED Equation.3 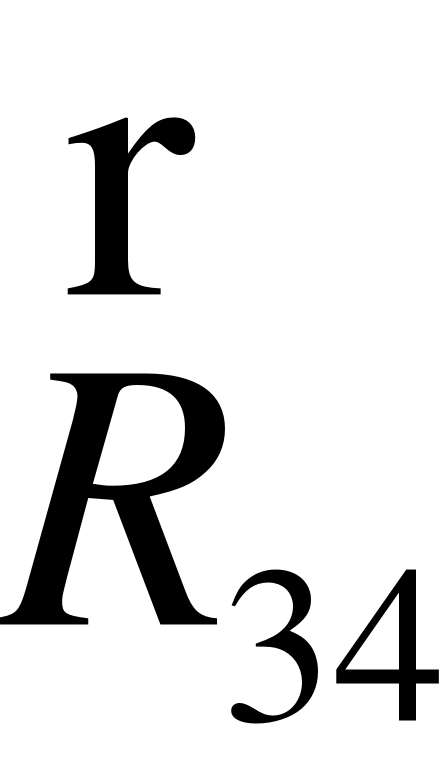
EMBED Equation.3 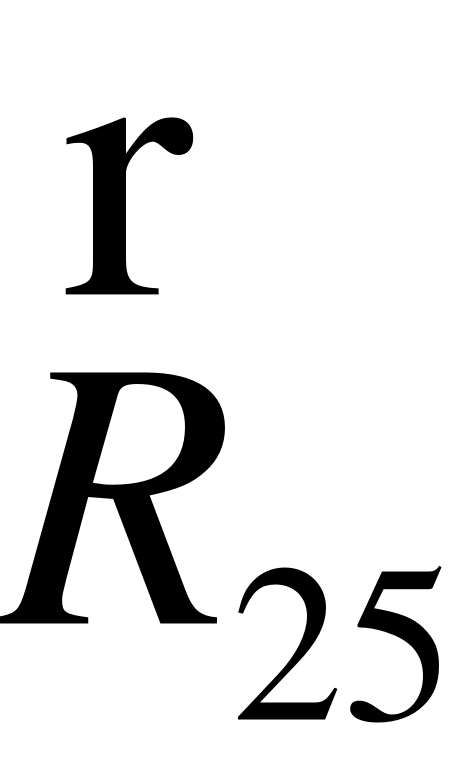
Рис. 5. Розрахункова схема для структурної групи 4-5
EMBED Equation.DSMT4 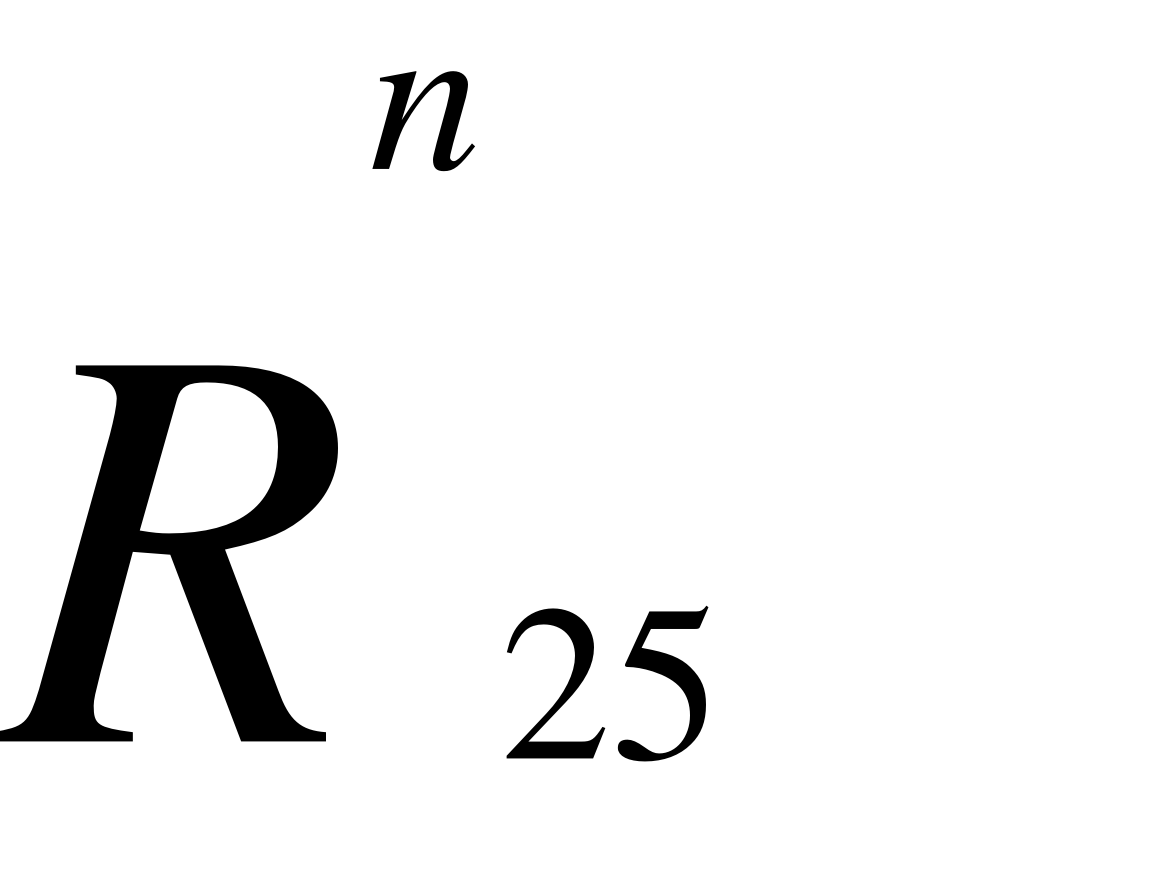
EMBED Equation.DSMT4 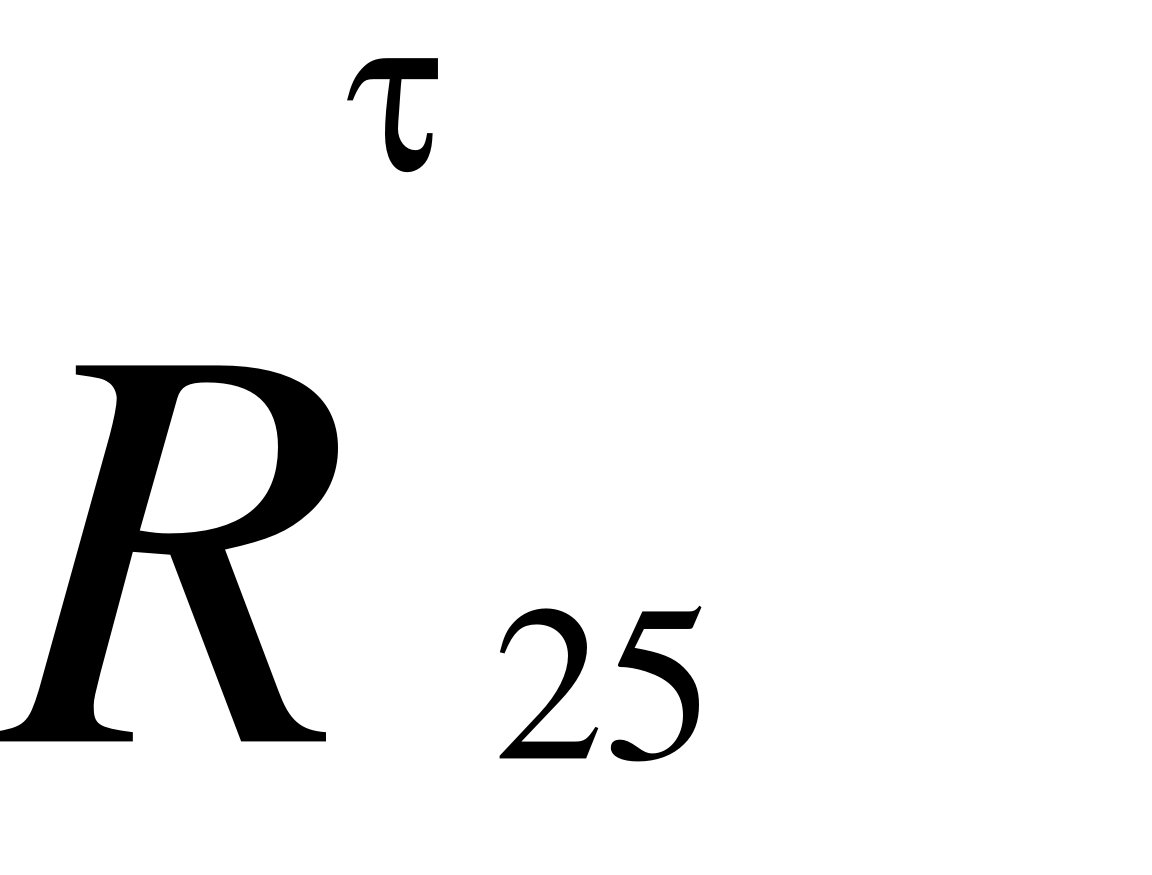
EMBED Equation.DSMT4 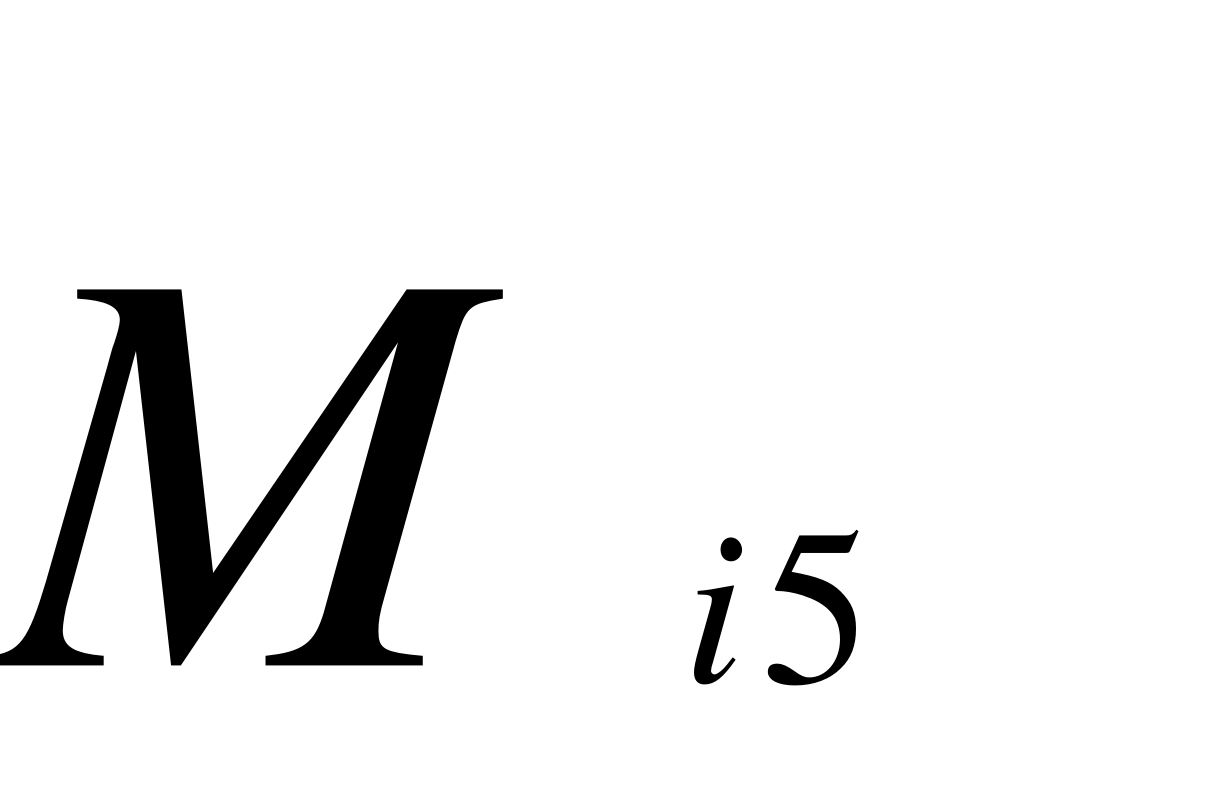
EMBED Equation.DSMT4 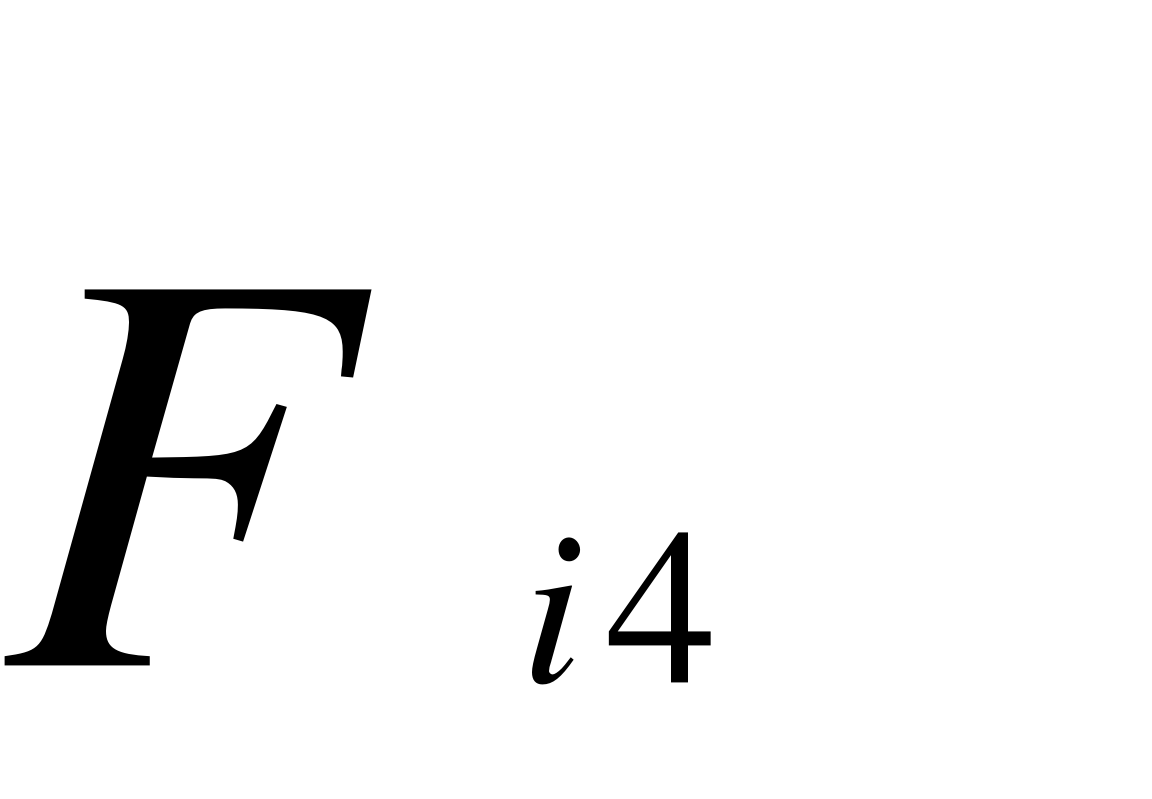
EMBED Equation.DSMT4 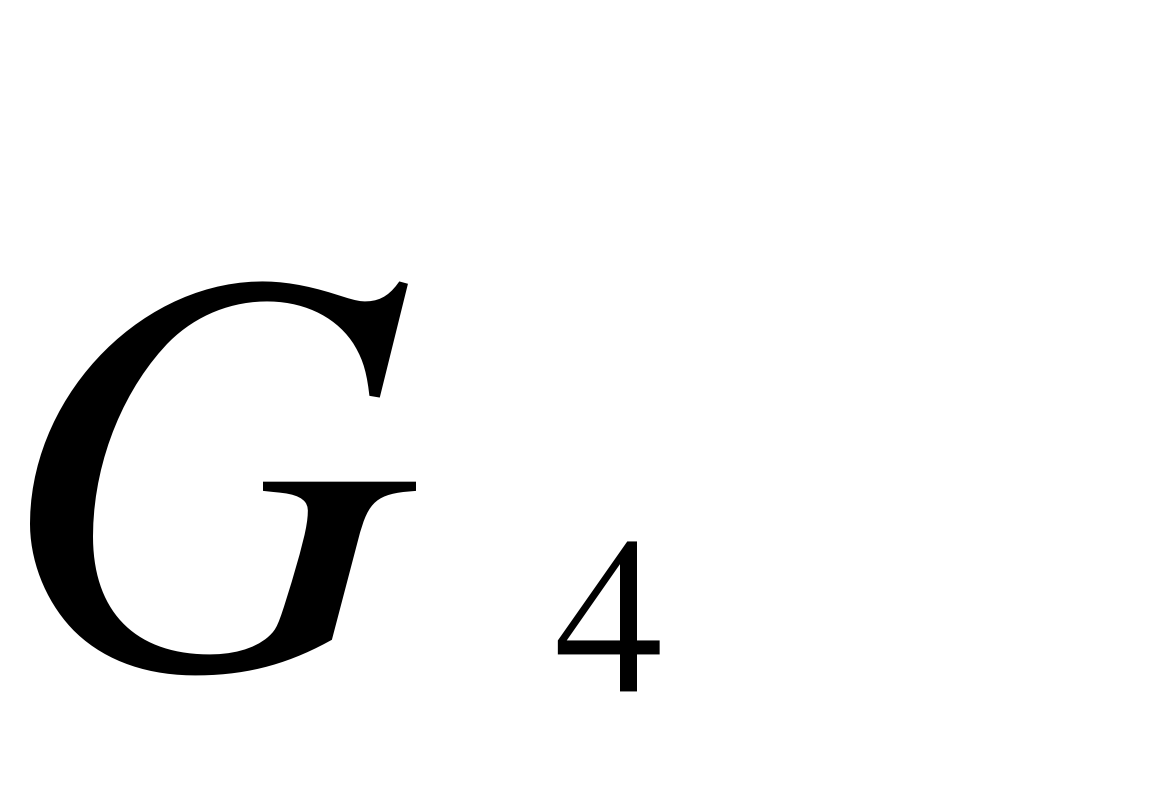
EMBED Equation.DSMT4 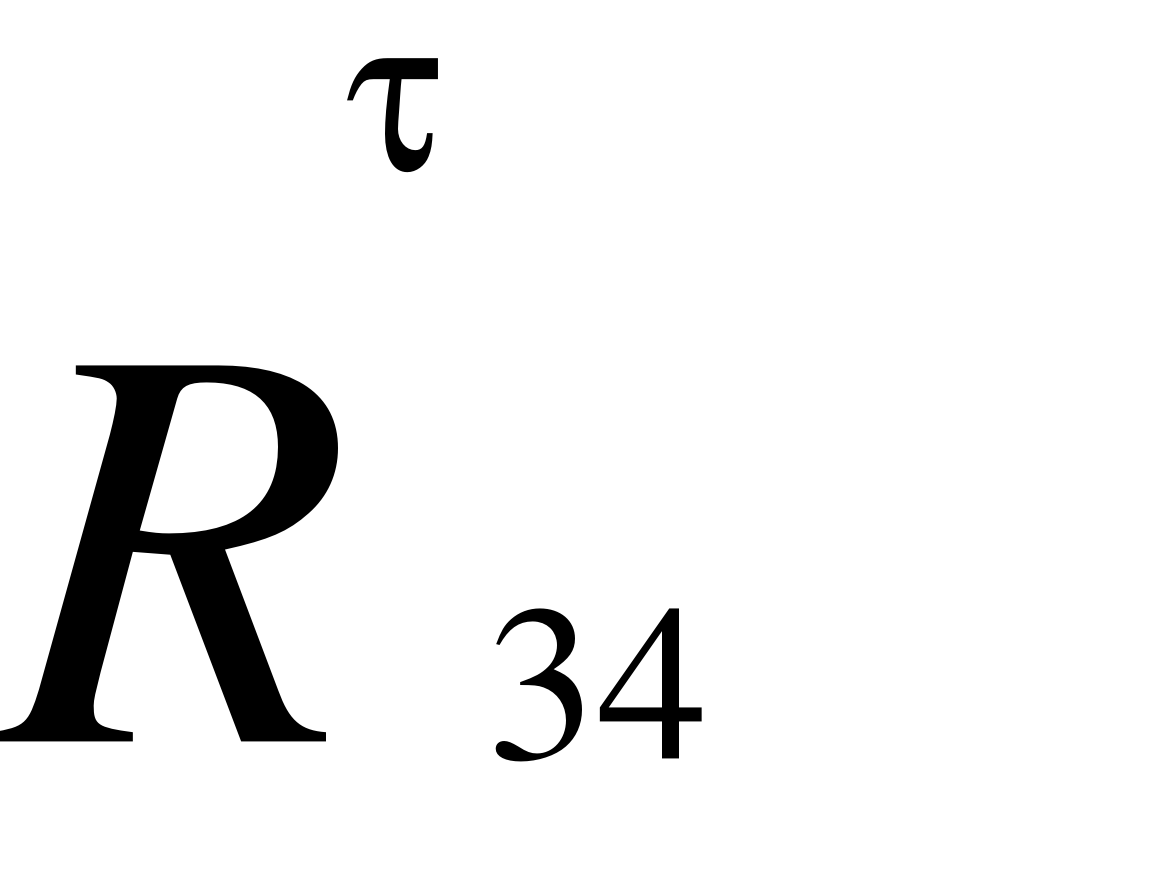
EMBED Equation.DSMT4 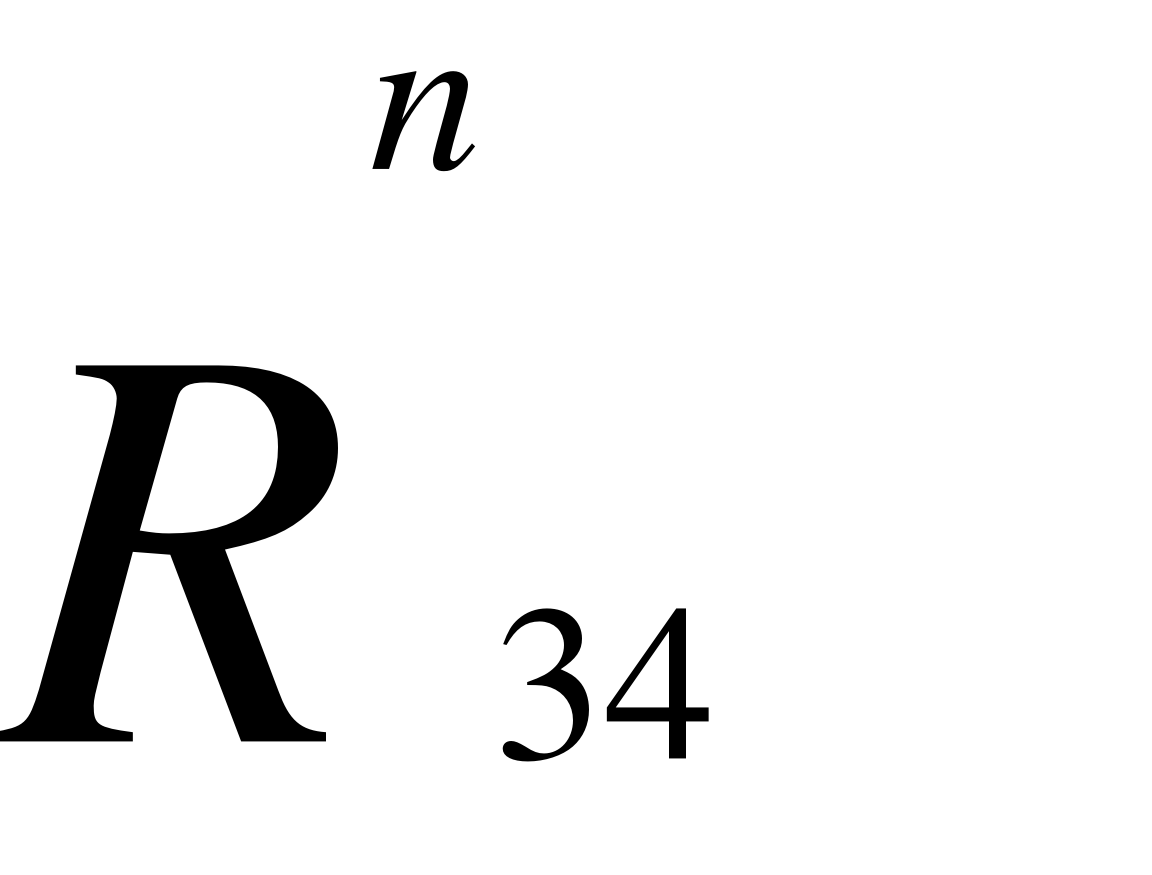
EMBED Equation.DSMT4 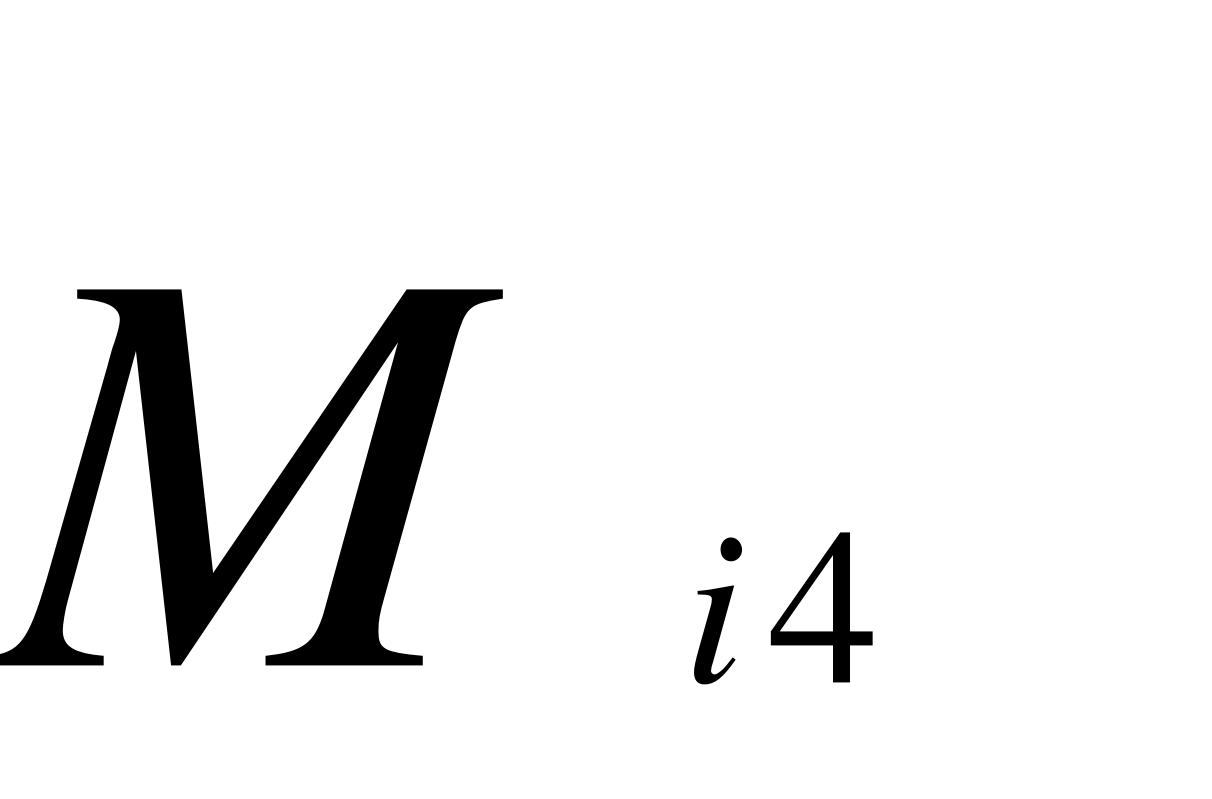
EMBED Equation.DSMT4 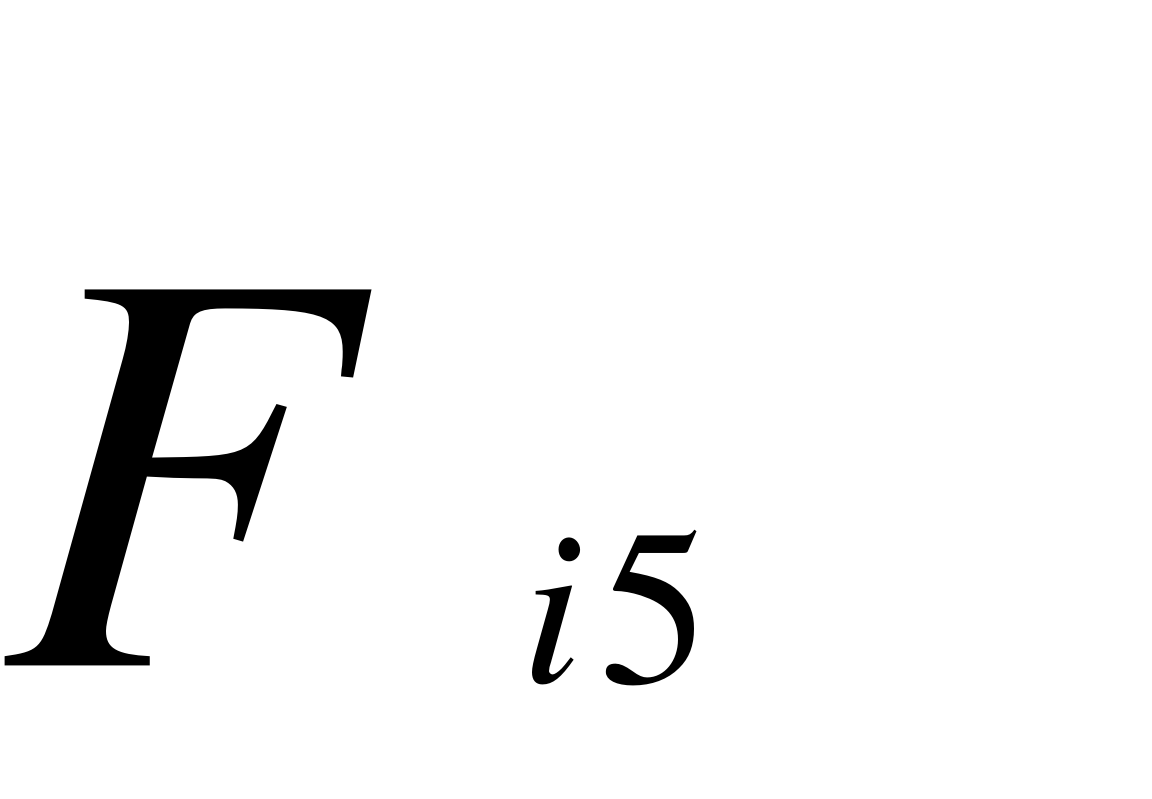
D
F
C
h1
h5
h2
h3
h6
В
S4
S5
4
5
EMBED Equation.DSMT4 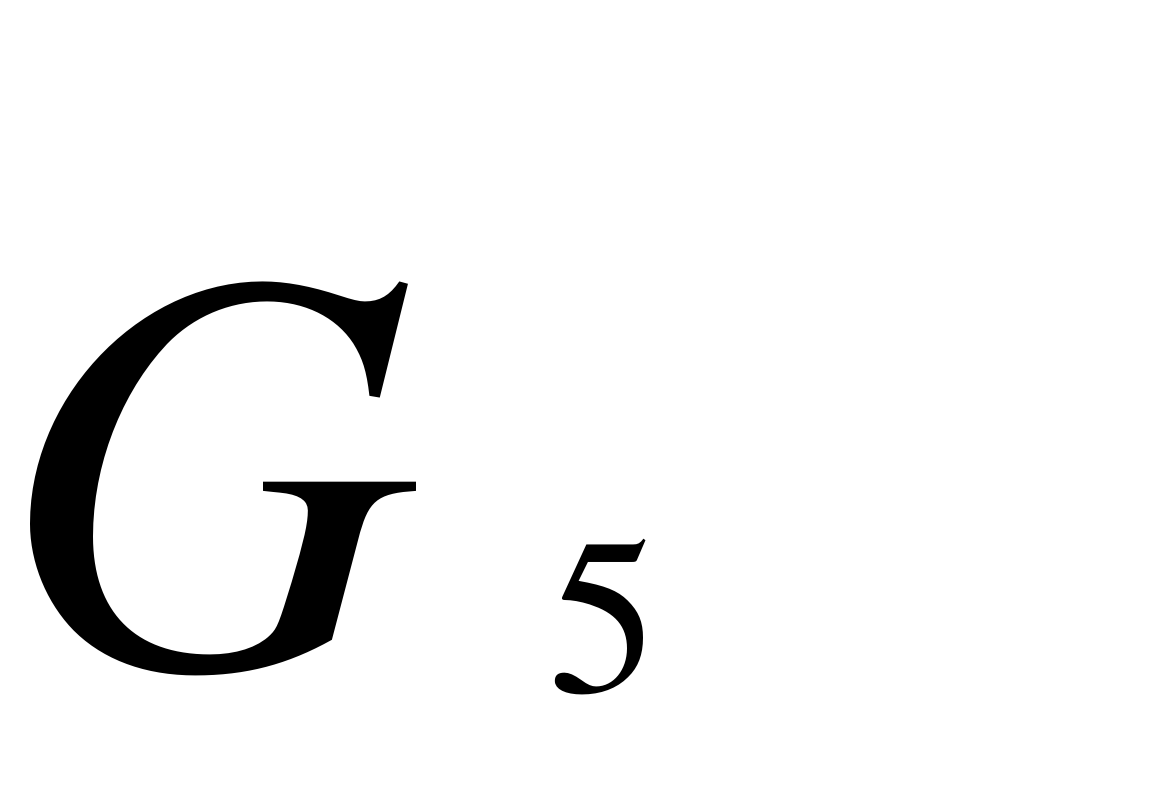
EMBED Equation.DSMT4 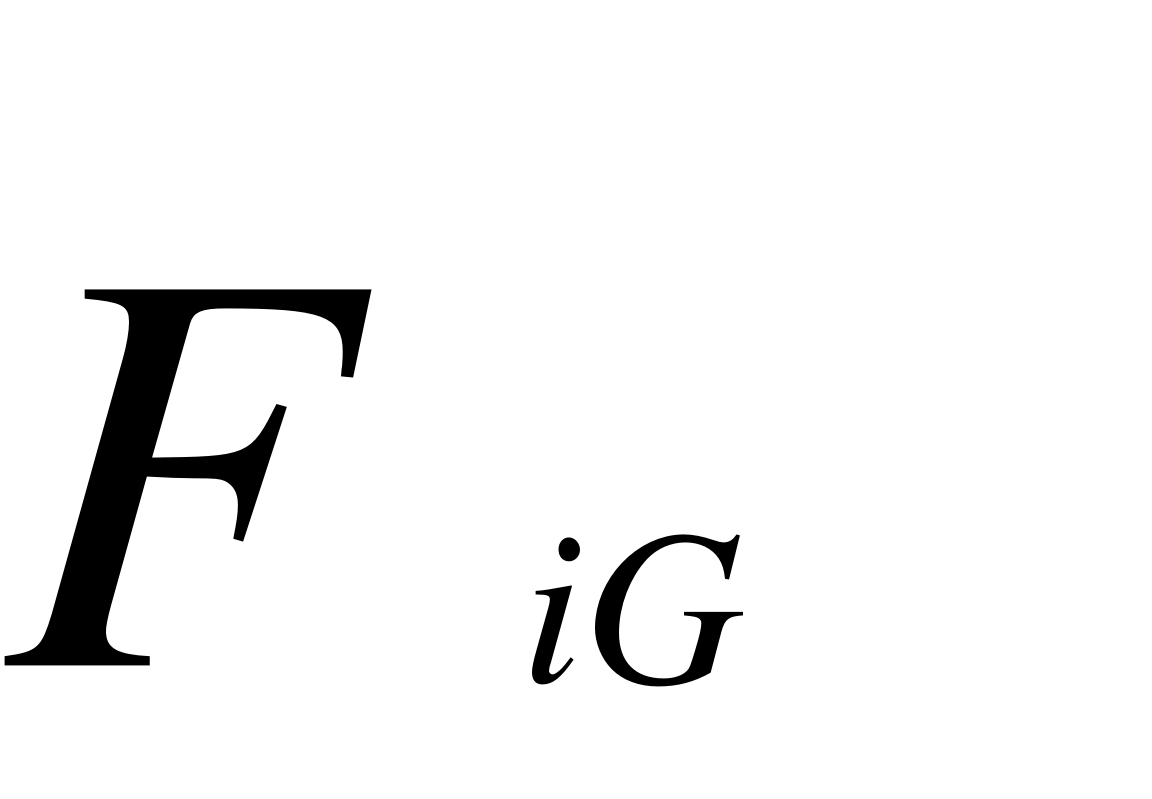
EMBED Equation.DSMT4 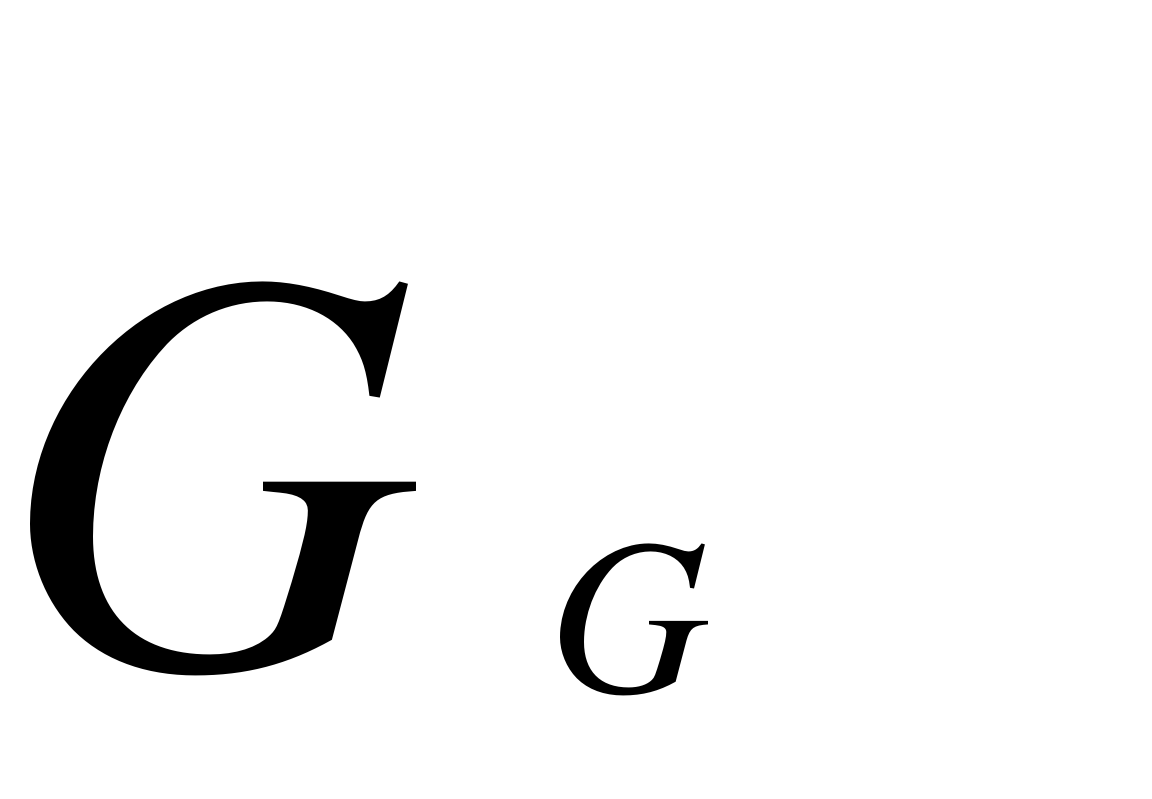
(28)
(27)
3
6
А
В
D
E
s3
s6
EMBED Equation.3 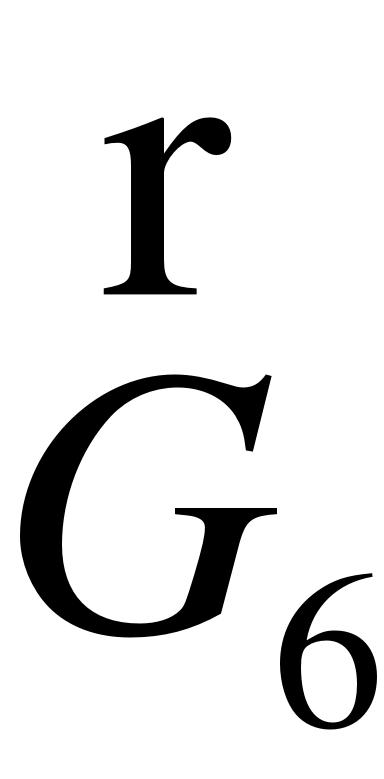
EMBED Equation.3 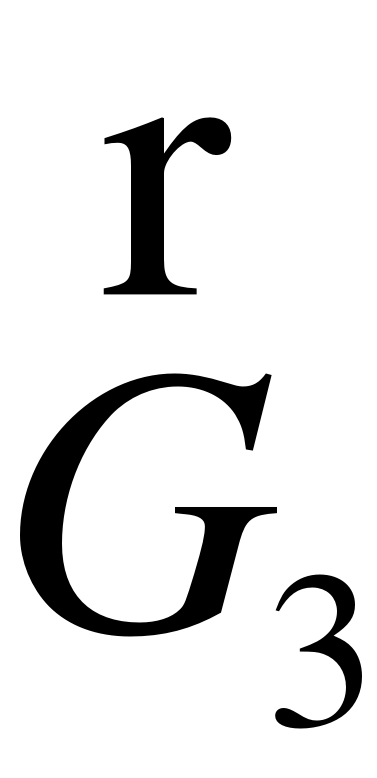
EMBED Equation.3 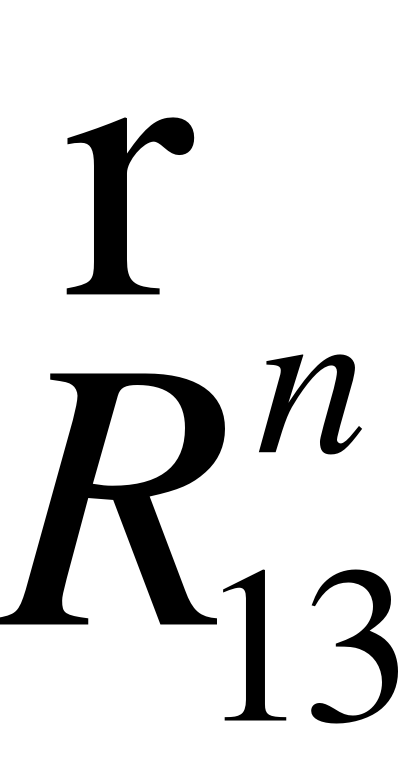
EMBED Equation.3 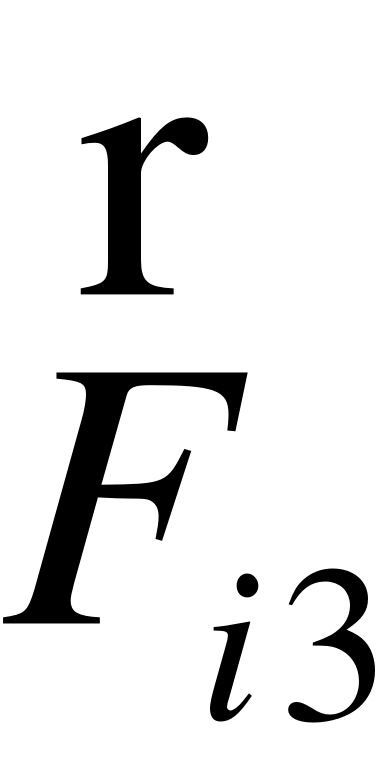
EMBED Equation.3 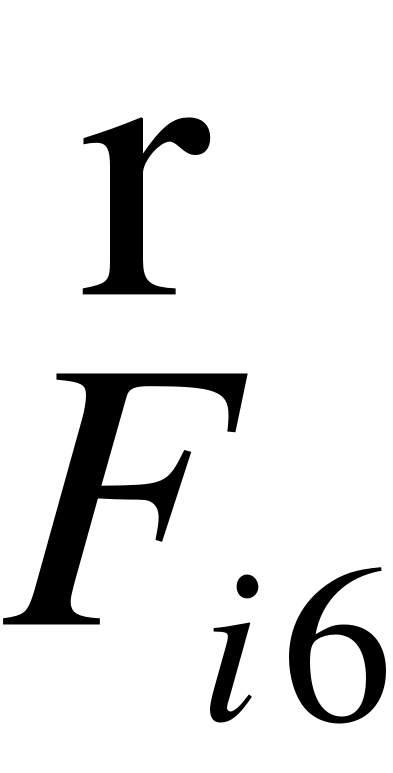
EMBED Equation.3 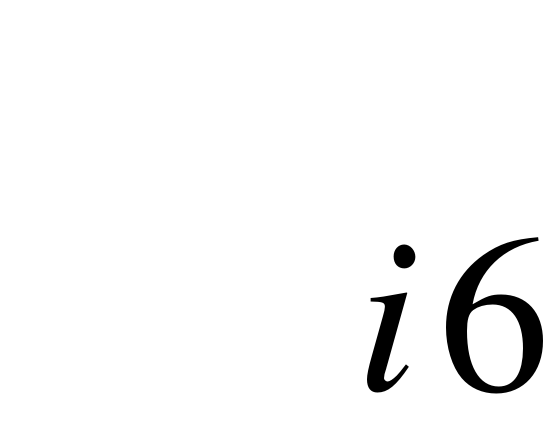
EMBED Equation.3 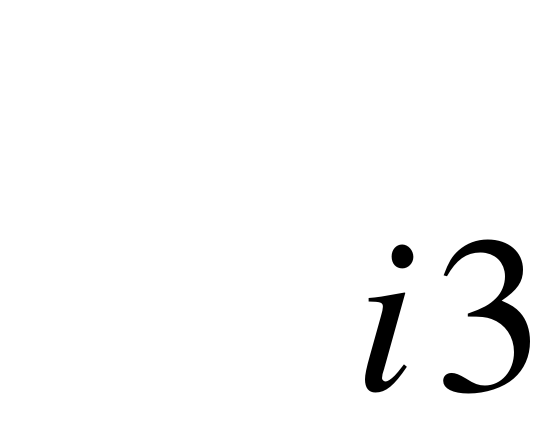
h5
h3
h1
h2
EMBED Equation.3 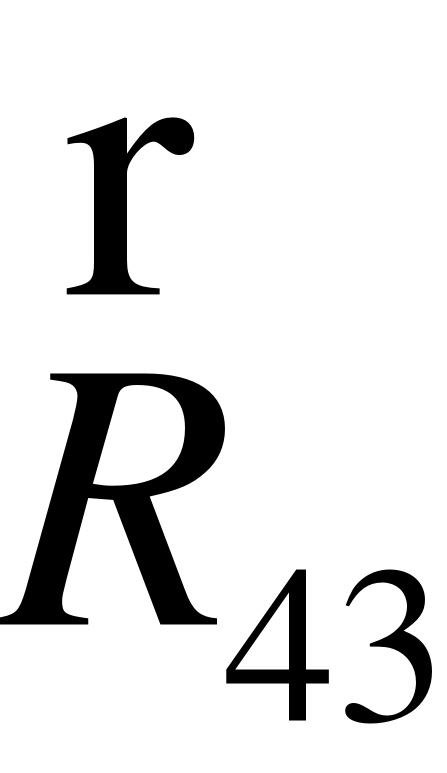
h6
EMBED Equation.3 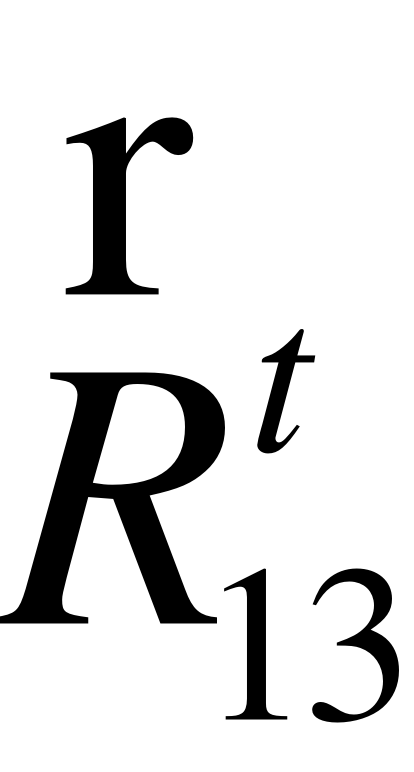
EMBED Equation.3 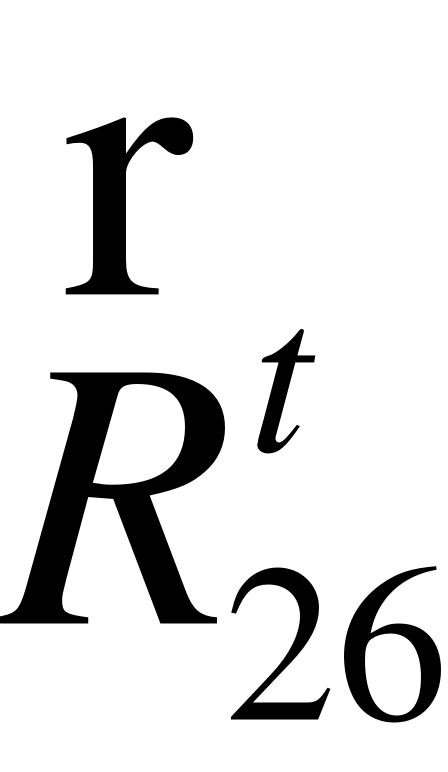
EMBED Equation.3 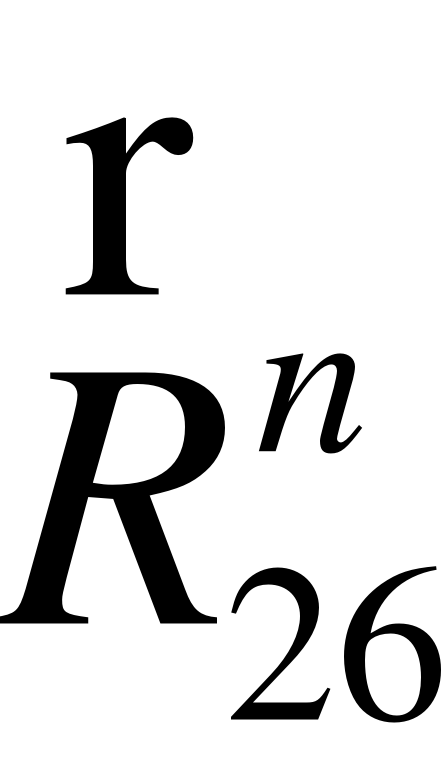
Рис. 7. Схема навантажень структурної групи Ассура (3-6)
Рис. 8. Векторний багатокутник сил, що діють на групу (3-6)
r
t
s
n
o
f
u
zf
EMBED Equation.3 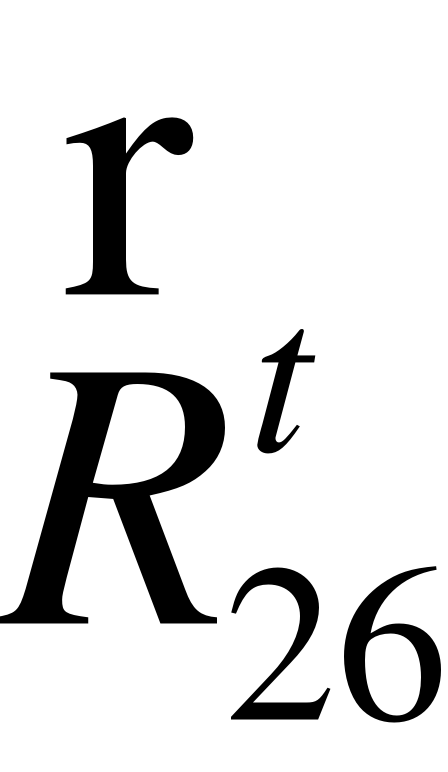
EMBED Equation.3 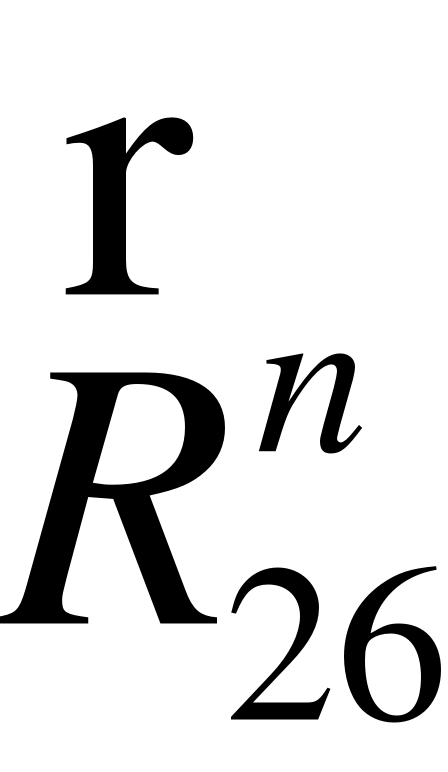
EMBED Equation.3 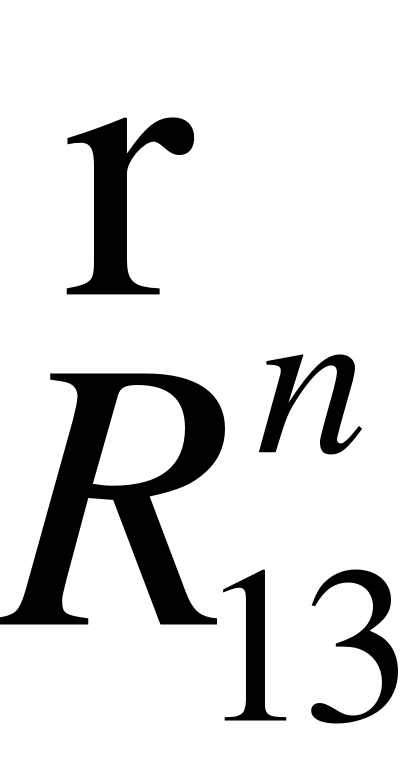
EMBED Equation.3 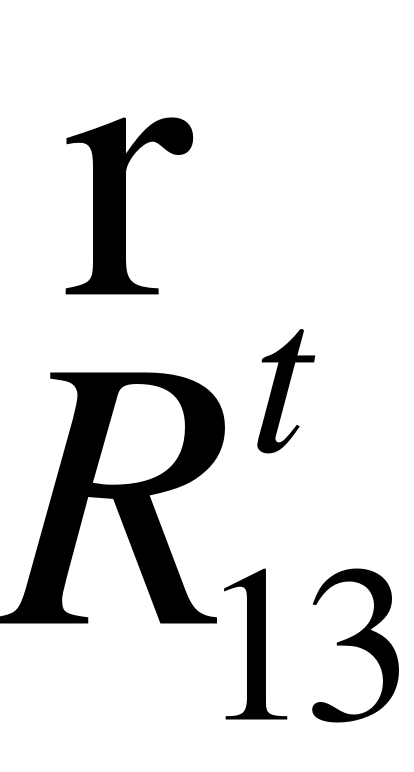
EMBED Equation.3 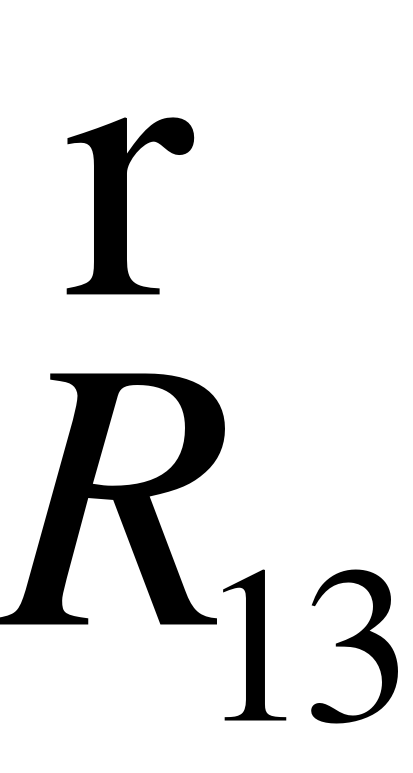
EMBED Equation.3 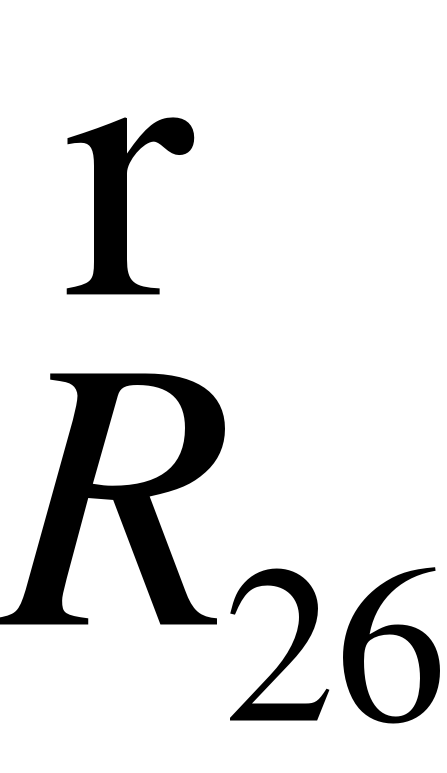
BE
AD
p
x
y
о
EMBED Equation.3 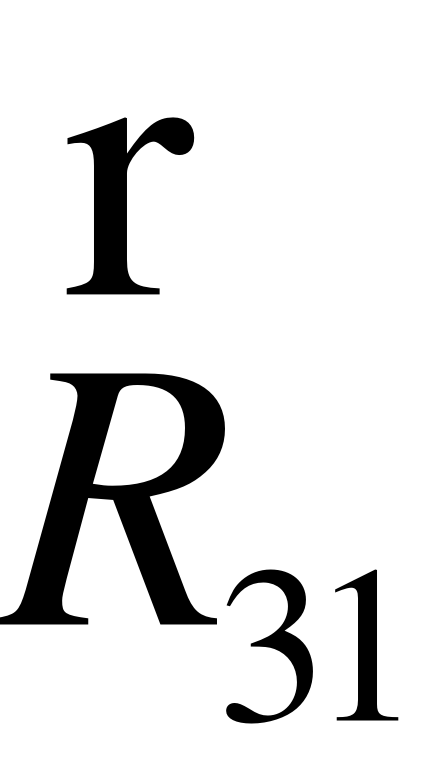 R52
R52
EMBED Equation.3  R52
R52
Рис.9. Схема до визначення зусилля на шток гідроциліндра 1
EMBED Equation.3 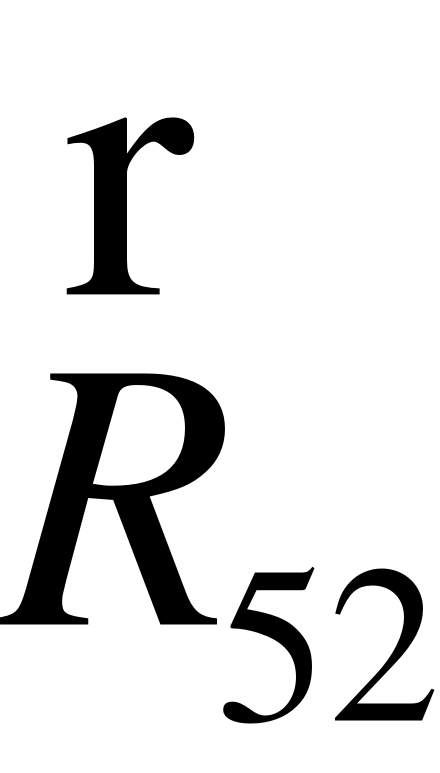 R52
R52
EMBED Equation.3 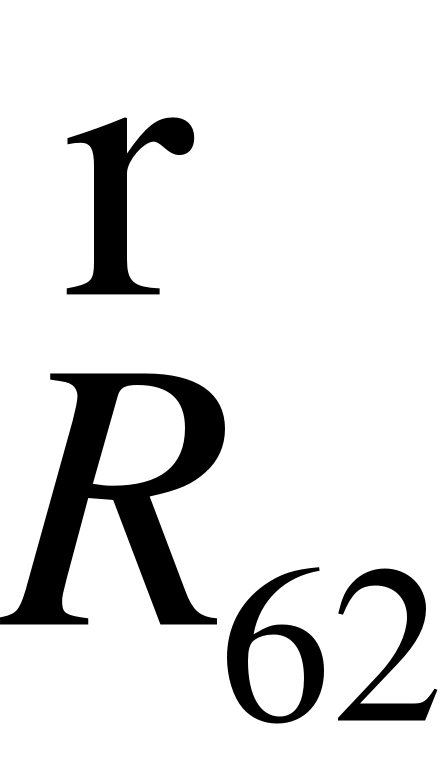 R52
R52
EMBED Equation.3 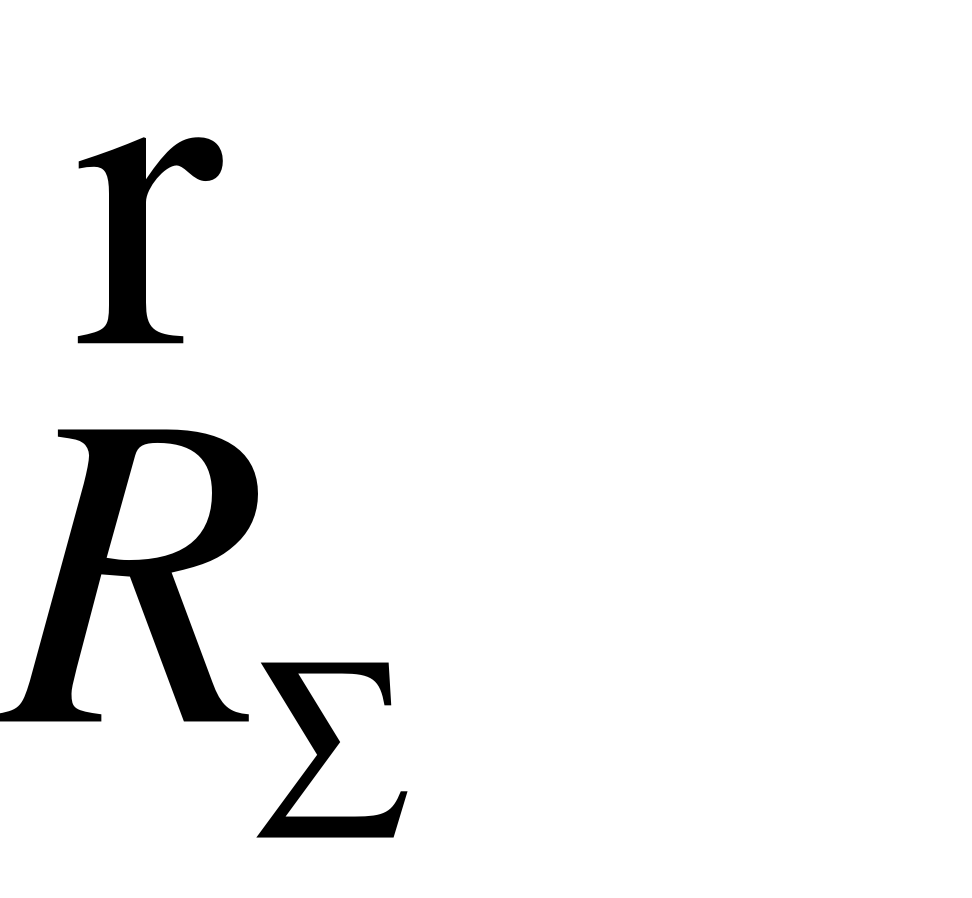
a
b
c
y
x
F2
Рис.10. Схема до визначення зусилля на штоку гідроциліндра 2
КІНЕТОСТАТИЧНИЙ РОЗРАХУНОК СХЕМИ ЗБАЛАНСОВАНОГО МАНІПУЛЯТОРА