КІНЕМАТИЧНИЙ АНАЛІЗ МЕХАНІЗМІВ МЕТОДОМ ПЕРЕТВОРЕННЯ КООРДИНАТ (МЕТОД Ю.Ф.МОРОШКІНА)
Лекція №11
КІНЕМАТИЧНИЙ АНАЛІЗ МЕХАНІЗМІВ МЕТОДОМ ПЕРЕТВОРЕННЯ КООРДИНАТ
(МЕТОД Ю.Ф.МОРОШКІНА).
Основні теоретичні положення перетворення координат. Практичне застосування методу Морошкіна.
Метод перетворення координат можна застосовувати як для плоских так і просторових механізмів. Особливо зручний при дослідженні просторових механізмів.
Для прикладу спочатку розглянемо плоский незамкнений кінематичний ланцюг механізму маніпулятора, який складається з чотирьох ланок, кожна з однією обертовою парою V класу (рис. 9.4.). Осі всіх кінематичних пар паралельні, тому число ступенів вільності можна визначити за формулою Чебишева
W=3n-2p5=3*3-2*3=3.
Рис. 9.4. Механізм маніпулятора.
За три узагальнені координати приймаємо кути . При кінематичному аналізі ці кути задаються функціями часу. Крім того, з кінематичної схеми відомо довжини ланок l1, l2 і координати xE3, yE3 деякої точки Е3 на ланці 3 в системі координат x3O3y3. Необхідно знайти траєкторію точки Е3 відносно стояка О у системі координат x0O1y0 .
Розглянемо точки Е2, Е1, Е0 , які в даний момент збігаються з точкою Е3 , але належать відповідно ланкам 2, 1, 0 (стояк). На основі рівнянь перетворення плоских декартових координат при розміщенні їх так, як зображено на рис. 1, одержимо
(1)
Аналогічно запишемо рівняння переходу до системи координат x1O1y1
(2)
І далі здійснюємо перехід до системи координат x0O1y0
(3)
Розв”язування системи шести рівнянь з шести невідомими дає можливість знайти положення точки Е3 у системі координат x0O1y0 , тобто положення точки Е0 . Для розв”язування системи рівнянь доцільно використовувати ПК.
Для встановлення певних правил обчислення і скорочення запису використовують матричну форму запису рівнянь перетворення координат. Коефіцієнти рівнянь (1-3), які відповідають повороту осей і переносу початку координат, дають матрицю порядку (2х3):
і т.д.
Щоб мати справу лише з квадратними матрицями, які можна множити, додаємо до кожних двох рівнянь перетворення координат третє рівняння тотожності . Тоді коефіцієнти правих частин рівнянь (1-3) з доданням тотожності утворять квадратну матрицю третього порядку:
.
Аналогічно коефіцієнти правих частин рівнянь (2,3) з доданням тотожності дають матриці:
;
.
Аналогічно коефіцієнти правих частин рівнянь (1-3) з доданням тотожності 1=1 дають матриці:
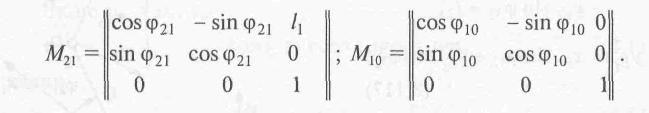
Ліві частини рівнянь (1-3) з доданням тотож�ності 1=1 дають матриці-стовпці третього порядку:
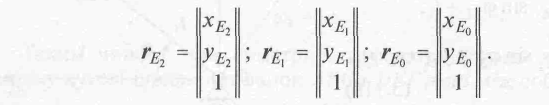
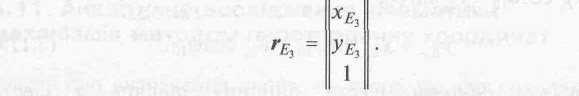
Тепер рівняння (1-3) з доданням тотожності 1=1 запишемо у вигляді, який відповідає добутку квадратної матриці третього порядку та матриці-стовпця того самого порядку:
(4)
Підставивши значення перших двох рівнянь у третє рівняння системи (4), можна визначити координати хе і уЕ :
(5)
Перемножимо матриці М10 М2І. Використовуючи правило множення рядка на стовпець для елемента першого рядка і першого стовпця, одержуємо
Аналогічно визначаємо всі Інші елементи матриці М10, М21 і, користуючись відомими тригонометричними формулами для суми кутів, записуємо
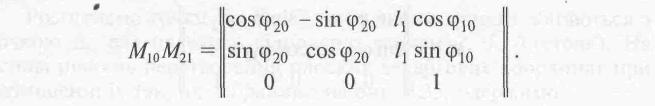
Помножимо одержану матрицю на М32:

де 30= 21+ 10
Помноживши квадратну матрицю М10М21М32 на стовпцеву матрицю rE3 і повернувшись до звичайної координатної форми, отримаємо
(6)
Зрозуміло, що рівняння (6) можна було б одержати із системи рівнянь (1-3), використовуючи звичайні алгебраїчні перетворення, але при цьому обчислення були б більш громіздкими. Перевага матричної форми запису полягає головним чином у використанні формули множення матриць, яка дає змогу однаково послідовно виконувати перетворення координат.
Зауважимо, що рівняння (6) для визначення координат точки Е3 можна одержати також з рівнянь проекцій контуру О1О2О3Е3 на нерухомі осі координат. Це спрощення, проте, можливе лише для плоских механізмів. При кінематичному аналізі просторових механізмів, навпаки, метод перетворення координат простіший за метод проекцій.
Використовуючи рівняння (6), можна знайти координати будь-якої точки на ланці 3, тобто цілком визначити її положення. Аналогічно встановлюють взаємні положення інших ланок механізму, причому для їхнього знаходження завжди одержують систему лінійних рівнянь.
Рівняння перетворення координат. Загальні рівняння перетворення
(7)
координат систем xi yi zi і xj yj zj
де аі ,bі ,cі — координати початку системи координат xjyjzj у системі координат xiyizi; а11, а12,... - коефіцієнти при координатах xjyjzj: (напрямні косинуси), тобто
(8)
Рівняння (7) можна записати у матричній формі:
(9)
Напрямні косинуси можна також виразити через кути Ейлера. Нагадаємо, що для відрахунку кутів Ейлера відмічається лінія вузлів ON, тобто лінія перетину площини XjOyj З площиною ХiОуi (рис. 3.36). Системи координат ХiОуi і XjOyj праві, тобто найкоротший поворот осі Охi до осі Оуі здійснюється проти руху годинникової стрілки, якщо дивитися з додатного напрямку осі Оzi. Додатний напрямок лінії вузлів такий, що найкоротший поворот від осі Оzi, д`о осі Ozj здійснюється проти руху годинникової стрілки. Кут між віссю Охi, і лінією вузлів називають кутом прецесії ji, кут між лінією вузлів і віссю Oxj — кутом чистого обертання ji , кут між осями Оzi, і Оzj - кутом нутації ji .
Кути ji і ji відраховуються проти руху годинникової стрілки, якщо дивитись з додатного напрямку осі Оzi або осі Оzj . Якщо початки координат систем хiОуi,- і хjОуj не збігаються з точкою О, то для відрахунку кутів Ейлера треба через Оj, провести осі, паралельні осям систем хiОуi.
Матриці кінематичних пар. Щоб встановити зв'язок між на�прямними косинусами у рівнянні (7) і кутами Ейлера, розглянемо окремий випадок перетворення декартової системи координат за умови, що осі Оzi i осі Оzj збігаються (рис. 3.37). У цьому випадку маємо обертання у площині хiОуi . Тоді координати точки E у системі хiОуi можна записати так:
(10)
За Ейлером, якщо хiОуi і хjОуj - дві прямокутні системи координат, що мають однакову орієнтацію, то перетворення однієї системи на іншу можна замінити трьома перетвореннями, кож�не з яких є поворотом навколо осей на кути Ейлера (ji , ji , ji ). Перший поворот системи координат хiуizi, здійснимо на кут ji , (рис. 3.38, а) навколо осі zi . При цьому розглянемо систему координат Nizi, де вісь Oi перпендикулярна до осей Оzуi та ON і направлена так, що системи хiуizi і Nizi мають однакову орієн�тацію. Крім цього, ці системи мають спільну вісь Ozi, тому друга система може бути одержана поворотом першої навколо осі Ozi на деякий кут ji. Тоді, розглянувши положення обох систем у площині, яка перпендикулярна до осі Ozi (рис. 3.38, б), за аналогією з рівнянням (3.126), запишемо (на рис. 3.38, б— г у дужках вказані відповідні осі, рис. 3.37):
xi=ncosji - isinji ; (11)
yi= nsinji + icosji ,
де хi, уi, — координати точ�ки Е у системі координат хiОуi, a n, — у системі координат NOi (рис. 3.38, б).
Перейдемо від системи Nizi (рис. 3.38, а) до прямокутної системи Njzj (вісь Ozj перпендикулярна до осі ON, оскільки вісь ON лежить у площині XjOyj, вісь Oj перпендику�лярна до осей ON і Ozj і направлена так, щоб обидві системи Nizi і Njzj мали однакову орієнтацію). Система Njzj одержана поворотом системи координат Nizi навколо осі N на кут ji (рис. 3.38, в). За аналогією з рівнянням (3.126) записуємо
i= j cosji - zjsinji ;
zi= jsinji+ zjcosji , (12)
де j , zj координати точки Е у системі координат jOzj (рис. 3.38, в).
Система Nizi має таку саму орієнтацію, як і система хiуizi , тобто таку саму орієнтацію, як і система хjуjzj . Тому систему хiуizi одер�жуємо поворотом системи Njzj навколо осі Ozj на кут ji (рис. 338, г). Тоді за аналогією з рівнянням (3.126) маємо
(13)
де xjt yj — координати точки у системі координат х}Оуґ
Вилучимо із співвідношень (11-13) параметри n, i. Для цього підставимо значення j у першу залежність системи рівнянь (12) і визначимо
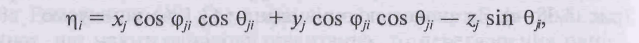
потім підставимо значення n, i у залежність (10), j - у другу залежність системи (3.128) і одержимо рівняння для визначення координат точки Е у системі хiуizi.
Порівнюючи одержану систему рівнянь із рівняннями (7), можна записати матрицю коефіцієнтів для цих рівнянь:
(14)
Матрицю Мji можна назвати матрицею кінематичної пари.
Для сферичної пари III класу кути Ейлера є змінними параметрами, а координати аi ,bi , і сi — постійними.
Для сферичної пари з пальцем (рис. 3.39) тільки два кути будуть незалежними.
Вісь пальця (рис. 3.39, б) зручно прийняти за вісь Ojzj, а вісь пазу (вісь, перпендикулярну до площини пазу) - за вісь Оixi, (або паралельно осі Oixi якщо початки координат Оi і Оj не збігаються). Тоді кут прецесії ji = 0, кут чистого обертання ji , який вимірюється між осями xiyj , є кутом повороту осі пальця, кут нутації ji - кутом повороту навколо осі пазу. За цих двох умов матриця сферичної пари з пальцем одержується з матриці (15) при ji = 0:
Для ланок обертової пари (рис. 3.40) вісь Ojzj направимо вздовж осі цієї пари, найкоротшу відстань li між осями Ojzj i Oizi сумістимо з віссю Оixi , а початок координат Оj, розмістимо на відстані lji , від осі Оixi. Тоді кут нутації ji = const, кут прецесії ji = 0 і з врахуванням прийнятих позначень отримаємо з (15) матрицю обертової пари:
(16)
Матрицю поступальної пари одержимо з матриці (17), якщо вважатимемо параметр lji =sji - змінною величиною, а кут ji= 0. Кут ji у цьому
(17)
випадку є кутом між віссю Oizi і віссю поступальної пари, а величина li - дорівнює найкоротшій відстані між цими осями. Таким чином,
За цих умов, якщо за�мість поступальної пари буде гвинтова, відстань lji = sji треба вважати змінною величиною, яка зв'язана з кутом повороту ji співвідношенням sji=hjiji/(2), де hji - крок гвинтової лінії.
Нарешті, якщо ланки i та j утворюють циліндричну пару, то в матриці (17) треба вважати незалежними дві величини: lji = sji та ji .
Усі вказані матриці мають порядок (3x4). Якщо необхідно мати тільки квадратні матриці, які можна множити, то до рівнянь перетворення координат (7) додають тотожність 1=1 і відповідно у всіх матрицях з'являється четвертий рядок, який містить у собі нулі у перших трьох стовпцях і одиницю у четвертому.
PAGE 2
КІНЕМАТИЧНИЙ АНАЛІЗ МЕХАНІЗМІВ МЕТОДОМ ПЕРЕТВОРЕННЯ КООРДИНАТ (МЕТОД Ю.Ф.МОРОШКІНА)