ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ КАБЕЛЬНЫХ ЛИНИЙ СВЯЗИ

ЛЕКЦИЯ 18. ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ КАБЕЛЬНЫХ ЛИНИЙ СВЯЗИ

Измерение Rшл, Rиз, С, Rасс. Измерительные приборы

ПЕРВИЧНЫЕ ПАРАМЕТРЫ ПЕРЕДАЧИ

Электрические свойства линий связи и качество передачи по ним полностью характеризуются первичными параметрами передачи: активным сопротивлением R, индуктивностью L, емкостью С, проводимостью изоляции G. Эти параметры не зависят от напряжения и передаваемого тока, а определяются лишь конструкцией линии, используемыми материалами и частотой тока.

По физической природе параметры линии аналогичны параметрам электрических контуров, составленных из элементов R, L, С. Разница лишь в том, что в контурах эти параметры являются сосредоточенными, а в линиях они равномерно распределены по всей их длине. Принято определять параметры линий связи на 1 км длины. На рис. 18.1 представлена эквивалентная схема участка цепи связи. Здесь включенные последовательно R и L (продольные) образуют суммарное сопротивление Z=R+jL, a G и С (поперечные) —суммарную проводимость Y=G+jC.

Параметры R и L характеризуют процессы в металлических частях линии (проводники, экраны, оболочки), параметры G и С — процессы в диэлектрике (изоляция кабеля, изоляторы воздушных линий).

При прохождении сигналов связи по линии уменьшаются напряжение и ток, так что мощность сигнала, проходящего в конец линии, существенно меньше начальной.

Рис. 18.1. Эквивалентная схема цепи связи

R и G обусловливают потери энергии: первый— потери на тепло в проводниках и других металлических частях (экран, оболочка, броня), второй — потери в изоляции. Если бы удалось создать линию с проводниками, обладающими сверхпроводимостью (R =0) и идеальной изоляцией (G=0), то передача электромагнитной энергии по такой линии проходила бы без потерь.

Активное сопротивление цепи R складывается из сопротивления проводников самой цепи и дополнительного сопротивления, обусловленного потерями в окружающих металлических частях кабеля (соседние проводники, экран, оболочка, броня). При расчете активного сопротивления обычно суммируются сопротивление цепи постоянному току (Ro) и переменному току (R~): R=Ro-R~.

Сопротивление цепи зависит от материала, диаметра, длины проводников и наличия окружающих металлических масс и измеряется в омах на километр (Ом/км).

Индуктивность цепи L обусловлена появлением (индуцированием) электродвижущей силы (ЭДС) при изменении магнитного потока. При этом индуцированная ЭДС может быть вызвана как изменением магнитного потока в соседней цепи (взаимоиндукция), так и — в собственной цепи (самоиндукция) .

Индуктивность цепи складывается из внутренней индуктивности самих проводников и внешней индуктивности, обусловленной внешним магнитным потоком.

L=Lвт+Lвш

Индуктивность цепи зависит от материала, размеров проводников и расстояния между ними. С ростом частоты передаваемого тока уменьшается внутренняя индуктивность. Внешняя индуктивность остается постоянно:

Индуктивность измеряется в миллигенри на километр (мГн/км).

Емкость цепи С — аналогична емкости конденсатора, у которого обкладками служат поверхности провод ков, а диэлектриком — изоляционный материал. Емкость выражается отношением количества электричества напряжению: С= Q/U.

Емкость цепи зависит от диаметра проводников, расстояния между ми, свойств изоляционного матери и близости соседних металлических масс. Емкость практически постоянна в очень широком диапазоне частот

В кабельной технике емкость цепи принято называть рабочей емкостью в отличие от частичных емкостей, т.е. емкостей между любыми отдельными жилами и жилами — оболочкой кабеля.

Емкость цепи измеряется в нанофарадах на км (нФ/км).

Проводимость изоляции G xapaктеризует качество изоляции проводников цепи (диэлектрик кабеля, материал изоляторов). Под проводимое изоляции понимается явление частичной электропроводимости изоляционных материалов, в результате часть передаваемой по цепи энергии рассеивается в диэлектрике, т. е. происходит утечка тока. Проводимость изоляции складывается из проводимостей изоляции постоянному (Go) и переменному току (G~): G=G0+ G~

Проводимость изоляции постоянному току обратно пропорциональна величине сопротивления изоляции (Rиз), Go=1/Rиз Проводимость изоляции переменному току растет с увеличением частоты и существенно зависит качества диэлектрика — тангенс угла диэлектрических потерь (tg ), т. е. G~=Ctg

В результате проводимость изоляции определяется следующей формуле

Обычно величина GO=1/ Rиз — мала, поскольку сопротивление изоляции нормируется 1000—10000 МОм-км. Проводимость изоляции измеряется сименсах на километр (См/км).

первичные параметры передачи (R, L, С, G) от диаметра и материала проводников, расстояния между ними, изоляции, частоты и температуры.

Вторичные ПАРАМЕТРЫ ПЕРЕДАЧИ

Вторичными параметрами линии являются волновое (характеристическое сопротивление Zв и коэффициент распространения . Они широко используются для оценки эксплуатации технических качеств линии связи. При проектировании, сооружений и эксплуатации кабельных магистралей в первую очередь нормируются и контролируются именно вторичные параметры линии.

Волновое сопротивление ZB — это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, т. е. при условии отсутствия влияния на процесс передачи несогласованности нагрузок по концам линии. Волновое сопротивление свойственно данному типу кабеля и зависит лишь от его первичных параметров и частоты передаваемого тока.

Волновое сопротивление, Ом, рассчитывается по формуле

(4.14)

По своей физической природе величина ZB не зависит от длины кабельной линии и постоянна в любой точке цепи.

электромагнитная энергия, распространяясь вдоль кабельной линии, уменьшается по величине от начала к концу линии. Уменьшение или затухание энергии объясняется потерями ее в цепи передачи. Различают два вида потерь. Во-первых, потери её металлических элементах кабеля (токопроводящие жилы, экран, оболочка, броня). При прохождении тока по кабельной цепи происходит нагревание токопроводящих жил и других металлических элементов и создаются тепловые потери энергии. С ростом частоты эти потери увеличиваются: чем больше активное сопротивление цепи R, тем больше потери энергии в металлических элементах кабеля. Во-вторых, потери в изоляции (диэлектрике). Эти потери обусловлены несовершенством применяемых изоляционных материалов и затратами энергии на диэлектрическую поляризацию (G).

Потери в цепи передачи учитываются через коэффициент распространения у, который является комплексной величиной и может быть представлен суммой действительной и мнимой ее частей:

(4.15)

чем длиннее кабельная линия, тем больше изменяется передаваемая энергия (сигналы связи) по величине и фазе.

При передаче сигналов связи параметры и характеризуют соответственно затухание и изменение фаз тока, напряжения и мощности на участке кабельной цепи длиной 1 км и называются коэффициентом затухания и коэффициентом фазы.

Коэффициент распространения =+j одновременно определяет изменение сигнала как по абсолютной величине, так и по фазе на 1 км длины кабеля.

Логарифмируя обе части приведенных выше выражений, получаем формулы для расчета затухания, дБ: l = 20

al= (4.19)

Затухание в 1 дБ характеризует уменьшение по мощности в 1,26 раза, а по току или напряжению в 1,12 раза.

Между неперами и децибелами существует следующее соотношение: а (дБ) =20

Коэффициент фазы измеряется в радианах или градусах на 1 км (1 рад = 57,3°).

Характер изменения тока вдоль однородной кабельной линии показан на рис. 4.4. Как видно из графика, вектор тока уменьшается и изменяет фазу вдоль линии. Уменьшение тока происходит по экспоненциальному закону (el)

Рассмотрим далее зависимость вторичных параметров кабельной линии частоты. Для упрощения анализа этой зависимости выразим вторичные параметры кабельных линий ZB и сокращенными формулами, которыми ;но пользоваться для расчетов.

При постоянном токе (f=0)

(4.20)

Следовательно, для данного случая коэффициент затухания = , коэффициент фазы = 0, а волновое сопротивление

В диапазоне низких частот (f 800 Гц) индуктивность кабельных цепей невелика, и можно пренебречь величиной L по сравнению с R.В этом случае можно также не считаться с параметром G по сравнению с С , т. е. в низкочастотном диапазоне - R > L и G<С, тогда

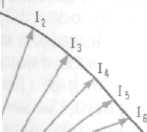
Рис. 18.2. Изменение тока по амплитуде и фазе вдоль линии

Таким образом, (4.22)

В свою очередь

(4.23)

При высокочастотной передаче по кабельной цепи имеют место следующие соотношения:

Тогда, применив к выражению коэффициента распространения формулу бинома Ньютона и ограничившись лишь первыми двумя членами разложения, получим:

(4.24)

Волновое сопротивление в этом случае можно рассчитывать по формуле

(4.25)

Формулы (4.24) и (4.25) обеспечивают достаточную точность при расчетах, начиная примерно с f = 30:50 кГц. Для кабельных цепей с искусственно увеличенной индуктивностью эти же формулы справедливы и при более низких частотах. В этом случае условие реализуется за счет значительной величины индуктивности цепи.

Во всех остальных случаях расчет коэффициентов затухания и фазы, а также волнового сопротивления следует производить по полным формулам.

На рис. 4.5 приведена типовая частотная зависимость коэффициента затухания и коэффициента фазы кабельной цепи. Коэффициент затухания а, равный при постоянном токе вначале растет резко, а затем более плавно. Коэффициент фазы растет от нуля почти по прямолинейному закону.

Характер частотной зависимости волнового сопротивления цепи кабеля иллюстрируется графиком, изображенным на рис. 4.6. Модуль волнового сопротивления с изменением частоты уменьшается от значения (при f = 0) до и сохраняет эту величину во всей области высоких частот. Угол волнового сопротивления равен нулю при постоянном токе (f = 0) и высоких частотах, а на частотах, близких к 800 Гц, имеет максимальное значение. В кабельных линиях угол всегда отрицателен и по абсолютной величине не превышает 45°, что свидетельствует о преобладании емкостной составляющей и емкостном характере волнового сопротивления кабелей.

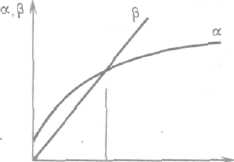
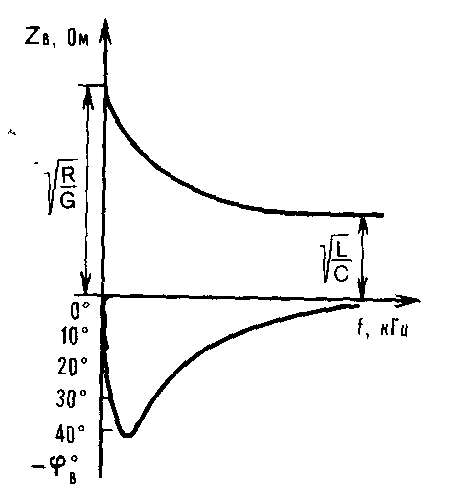
Рис. 4.5. Частотная зависимость коэффициента затухания и коэффициента фазы кабельной цепи

Рис. 4.6. Частотная зависимость волнового сопротивления кабельной цепи

В качестве примера укажем, кабель с кордельно-бумажной из изоляцией и диаметром жилы d= 1,2 имеет волновое сопротивление 490< при f = 800 Гц и 175 е-4° при f= 60 000 Гц.

СКОРОСТЬ РАСПРОСТРАНЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ЭНЕРГИИ ПО ЦЕПЯМ СВЯЗИ

Электромагнитная энергия распространяется по линии с определенной скоростью. Посланный в линию сигнал достигает конца лишь через соответствующий промежуток времени. Скорость передачи зависит от параметров цепи и частоты тока. Она определяется из выражения = /_ этой формулы видно, что скорость распространения является функцией частоты f= /2 и коэффициента фазы , который в свою очередь зависит от первичных параметров линии. Таким образом, если затухание цепи определяет качество и дальность связи, то коэффициент фазы обусловливает скорость движения энергии линии.

В диапазоне высоких частот, когда скорость распространения электромагнитной энергии не зависит от частоты и определяется лишь параметрами кабеля:

= / =1/LC(4.26)

При постоянном токе

можно отметить, что с ростом частоты скоро распространения электромагнитной энергии по кабельным линиям существенно возрастает. Так, если при постоянном токе скорость распространение электромагнитной энергии по линии составляет примерно 10000 км/с, то при токах высоких частот она достигает величины порядка 200 000 км/с, приближаясь к скорости света (с = 300000 км/с).

ЭЛЕКТРИЧЕСКИЕ ПРОЦЕССЫ В СИММЕТРИЧНЫХ ЦЕПЯХ

Под действием переменного поля происходит перераспределение электромагнитной энергии по сечению жилы; при этом имеют место следующие явления: поверхностный эффект, эффект близости и воздействие на параметры цепи окружающих металлических масс (соседних токопроводящих жил, экрана, оболочки, брони). Эти явления вызывают изменения электромагнитного поля и параметров цепей. Активное сопротивление R и емкость С возрастают, а индуктивность L уменьшается. Наиболее существенно возрастает сопротивление цепи: R = Rо + Rп.э + Rбл + Rм, где Ro — сопротивление постоянному току; R.э — сопротивление за счет поверхностного эффекта; Rбл — сопротивление за счет эффекта близости; RM — сопротивление, обусловленное потерями в окружающих металлических массах.

Поверхностный эффект обусловлен действием электромагнитной волны, распространяющейся по токопроводящей жиле. Силовые линии внутреннего магнитного поля Н (рис. 4.8), пересекая толщу жилы, наводят в ней вихревые токи /в.т. направленные по закону Ленца, т. е. против вращения рукоятки при поступательном движении буравчика. Вихревые токи /вт в центре жилы имеют направление, обратное движению основного тока, протекающего по ней, а на периферии их направления совпадают.

В результате взаимодействия вихревых токов с основным происходит такое перераспределение тока по сечению жилы, при котором плотность его возрастает к поверхности жилы. Это явление носит название поверхностного эффекта. Последний возрастает с увеличением частоты тока, магнитной проницаемости, проводимости и диаметра жилы. При достаточно высокой частоте ток протекает лишь по поверхности жилы, что вызывает увеличение ее активного сопротивления.

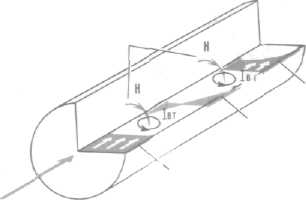
Рис. 4.8. Явление поверхностного эффекта

Эффект близости возникает по причине взаимодействия внешних полей. Как, видно из рис. 4.9, внешнее магнитное поле Н проводника а, пересекая толщу проводника б, наводит в ней вихревые токи. На поверхности проводника б, обращенной к проводнику а, вихревые токи совпадают по направлению с протекающим по ней основным токам (/ + /в.т), а на противоположной поверхности жилы б они направлены навстречу основному току (/—/в.т)- Аналогичное перераспределение токов происходит в проводнике а.

Рис.4.9 Эффект близости проводников

При взаимодействии вихревых токов с основным плотность результирующего тока на обращенных друг к другу поверхностях токопроводящих проводников а и б увеличивается, а на отдельных — уменьшается. Это явление («сближение» токов в проводниках а и б) носит название эффекта близости. Из-за этого неравномерного распределения плотности тока увеличивается активное сопротивление цепи переменному току.

Эффект близости также прямо пропорционален частоте, магнитной проводимости, проводимости и диаметр проводника и, кроме того, зависит расстояния между проводниками С приближением проводников к другу действие эффекта близости возрастает пропорционально квадрату расстояния. Если по двум соседним жилам токи проходят в одном направлении, то перераспределение их плотности из-за взаимодействия внешних электромагнитных полей приводит к увеличению плотности токов на взаимно отдаленных, поверхностях проводников а и б.

На рис. 4.10 показано распределение плотности токов в проводниках симметричной цепи, когда токи в них направлены противоположно (а) и когда они совпадают по направлению (б).

Рис. 4.10. Распределение плотности токов пары

Окружающие металлические массы за счет отражения от них электромагнитного поля также воздействуют на параметры цепи. Магнитное поле Н, создаваемое током, протекающим по жилам цепи, наводит вихревые токи /в.т в соседних цепях кабеля, в окружающем экране, металлической оболочке, броне и т. д. Вихревые токи нагревают металлические элементы кабеля и создают дополнительные тепловые потери энергии, что выражается как бы в «отсасывании» некоторой доли передаваемой энергии. При этом наиболее воздействуют близко расположенные к рассматриваемой цепи металлические элементы кабеля. Кроме того, вихревые токи создают поле обратного действия, которое воздействует на проводники цепи и также изменяет их параметры,

ПРОЦЕССЫ В ИЗОЛЯЦИИ

В отличие от токопроводящих жил, где имеются свободные электроны и действует ток проводимости /пр, в изоляционном материале нет свободных электронов, а имеются ионы и связанные диполи. Под действием переменного электромагнитного поля в изоляции происходит смещение диполей, их переориентация и поляризация (рис. 4.11). Поляризацией называется смещение положительных и отрицательных зарядов в изоляции под действием электрического поля.

Переменная поляризация обусловливает возникновение и действие токов смещения (емкостных токов) /См и вызывает затраты энергии на переориентацию диполей (потери в изоляционном материале — диэлектрике). Чем выше частота колебаний, тем сильнее токи смещения и больше потери. При постоянном токе эти явления отсутствуют.

Явления в изоляции, как отмечалось выше, полностью характеризуются двумя параметрами: емкостью С, определяющей способность поляризации и величину токов смещения, и проводимостью изоляции G, определяющей величину потерь в изоляционном материале.

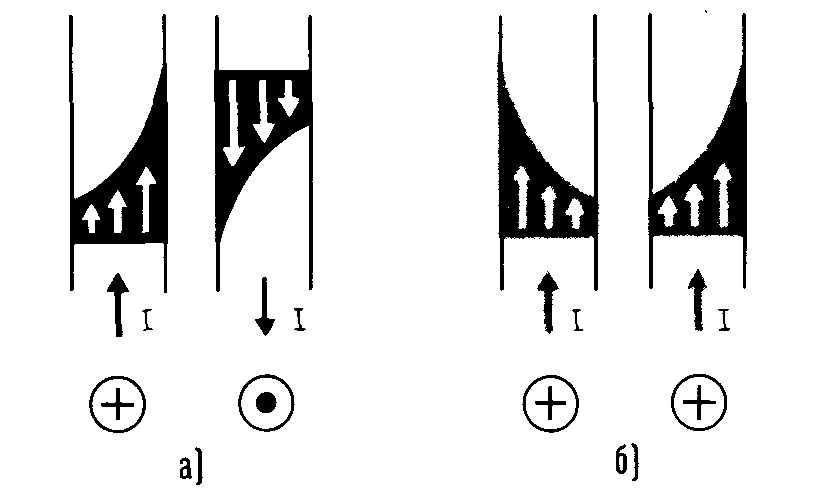
Рис. 4.11. Процесс поляризации: а) хаотическое расположение диполей; б) поляризация под действием электрического поля

ПЕРВИЧНЫЕ ПАРАМЕТРЫ СИММЕТРИЧНЫХ КАБЕЛЕЙ

Активное сопротивление симметричной кабельной цепи, Ом/км, состоит из сопротивления постоянному току Ro, сопротивления за счет поверхностного эффекта Rп.э, сопротивления за счет эффекта близости Rбл и сопротивления за счет потерь в окружающих металлических массах (соседние жилы, экран, броня) RM-

Сопротивление без учета потерь в металлических массах определяет по формуле:

R = Rо + Rп.э + Rбл + Rм (4.27)

Индуктивность, Гн/км, состоит из внешней и внутренней индуктивностей

(4.28)

Значения составляющих этой формулы приведены выше. Первая составляющая индуктивности превалирует над второй. С ростом частоты внутренняя индуктивность уменьшается.

Емкость, нФ/км, определяется по формуле

(4.29)

где — эффективная диэлектрическая проницаемость изоляции;

— поправочный коэффициент, характеризующий близость металлических проводников. Расчетные формулы коэффициента фазы для парной и звездной скруток приведены ниже: скрутка парная

скрутка звездная

Проводимость изоляции, См/км, состоит из двух частей, обусловленных утечкой постоянного и переменного токов, и определяется формулой

G = Gо+ G~ = l/Rиз+ Ctg. (4.30)

Здесь первый член Gо =l/Rиз — учитывает утечку постоянного тока за счет несовершенства изоляции. Сопротивление изоляции Rиз составляет для городских телефонных кабелей — 2000 МОм-км, а для кабелей дальней связи—10000 МОм-км. Второй член учитывает утечку вследствие потерь в изоляции кабеля при переменном токе. Здесь tg —тангенс угла диэлектрических потерь в изоляции кабеля.

В существующих кабелях второй член по абсолютной величине больше чем первый и проводимость изоляции можно рассчитывать по формуле G =Сtg

Кабели связи имеют, как правило, сложную комбинированную изоляцию,

состоящую из твердого диэлектрика (стирофлекс, полиэтилен, фторопласт и др,) и воздуха. Результирующие эффективные значения диэлектрической проницаемости э и тангенса угла диэлектрических потерь tg э сложной изоляции определяются электрическими свойствами и соотношением объемов составных ее частей.

ОСНОВНЫЕ ЗАВИСИМОСТИ первичных ПАРАМЕТРОВ СИММЕТРИЧНЫХ ЦЕПЕЙ

Рассмотрим графики зависимости первичных параметров линий связи R, L, С, G от частоты, диаметра проводника и расстояния между проводками.

С увеличением частоты (рис. 4.12) значение параметров R и G возрастает за счет потерь в проводниках на вихревые токи и в изоляции на диэлектрическую поляризацию, а индуктивность L уменьшается, так как из-за поверхностного эффекта уменьшается внутренняя индуктивность проводника. Емкость С от частоты не зависит. При увеличении расстояния между проводниками (рис. 4.13) параметры R, С, G закономерно уменьшаются, а индуктивность L возрастает.

L.G.C

Рис. 4.12. Зависимость первичных параметров цепи от частоты

Рис. 4.13. Изменение первичных параметров цепи с увеличением расстояния между проводниками

Снижение R обусловлено уменьшением потерь на эффект близости. Рост L связан с увеличением площади контура, пронизываемого магнитным потоком. Емкость С уменьшается, так как проводники удаляются друг от друга и уменьшается их взаимодействие.

С увеличением диаметра проводников (рис. 4.14) параметры С и G растут, a L уменьшается. Изменение активного сопротивления имеет сложный характер. Это обусловлено тем, что с увеличением диаметра проводника сопротивление постоянному току резко уменьшается, а сопротивление за счет поверхностного эффекта и эффекта близости растет. Поэтому вначале R снижается резко, а затем снижение замедляется.

Теоретически от температуры зависят все четыре первичных параметра.

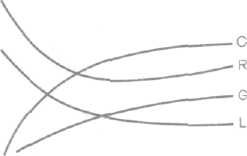
Рис. 4.14. Изменение первичных параметров цепи с увеличением диаметра проводников

Однако практически следует учитывать лишь температурную зависимость активного сопротивления. Изменение от температуры L, С, G весьма незначительно. Температурная зависимость активного сопротивления цепи определяется по формуле:

(4.35)

где Rt — сопротивление при температуре t°С, R20 — тоже при температуре 20°С; R — температурный коэффициент сопротивления, равный для меди 0,004 и для алюминия 0,0037.

С увеличением температуры сопротивление цепи растет (рис. 4.15). Физически это объясняется тем, что с увеличением температуры возрастает хаотическое движение атомов решетки и затрудняется прохождение электронов через нее.

Рис. 4.15. Зависимость электрического сопротивления от температуры

ВТОРИЧНЫЕ ПАРАМЕТРЫ СИММЕТРИЧНЫХ ЦЕПЕЙ

Вторичные параметры симметричных цепей ZB, , , следует рассчитывать по формулам, приведенным выше. В ряде случаев вторичные параметры выражают непосредственно через габаритные размеры цепей d, a и качество исходных материалов , tg .

Подставив в формулу ZB = YL/C значения L и С, получим значение волнового сопротивления симметричной цепи, Ом,

(4.36)

Коэффициент затухания симметричной цепи с медными проводника определится по формуле

=

дБ/км, путем подстановки в нее значений первичных параметров:

(4.37)

Коэффициент фазы, рад/с, определится формулой

= LС или = /с, (4.3J

где с — скорость света. Скорость распространения энергии , км/с.

(4.38)

Типовые частотные зависимости вторичных параметров цепи приведены на рис. 4.5—4.7.

КОАКСИАЛЬНЫЕ КАБЕЛИ СВЯЗИ

ЭЛЕКТРИЧЕСКИЕ ПРОЦЕССЫ В КОАКСИАЛЬНЫХ КАБЕЛЯХ

По коаксиальному кабелю можно передавать очень широкий спектр частот при малых потерях; этот кабель хорошо защищен от влияния соседних цепей и внешних помех. Кроме того, такая система связи в целом более экономична.

Взаимодействие электромагнитных полей внутреннего и внешнего проводников коаксиального кабеля таково, что его внешнее поле равно нулю. Это наглядно иллюстрируется на рис. 4.16, где показан характер изменения напряженности магнитного поля Ha и Hб каждого проводника (а и б) в отдельности. В металлической толще внутреннего проводника (а) магнитное поле Ha возрастает, а вне его — уменьшается по закону Ha= , где r —расстояние от центра провода до точки, в которой определяется напряженность поля. Поле Hб внешнего проводника (б) изображено в соответствии с законом электротехники: внутри полого цилиндра магнитное поле отсутствует, а вне его выражается таким же уравнением, как и для сплошного проводника Hб = —//2r, где r — также расстояние от центра полого проводника. Поэтому при определении внешних магнитных полей проводов принимается одинаковым и исчисляется от их общего центра (нулевой точки).

Токи в проводниках а и б равны по величине и обратные по знаку, поэтому магнитные поля внутреннего и внешнего проводников Ha и Hб в любой точке пространства вне кабеля также равны по величине и направлены в разные стороны. Следовательно, результирующее магнитное поле вне кабеля

Таким образом, линии магнитного поля коаксиального кабеля располагаются в виде концентрических окружностей внутри него.

Электрическое поле также замыкается внутри коаксиального кабеля по радиальным направлениям между проводниками а и б. Поэтому в коаксиальном кабеле из-за отсутствия внешнего поля нет потерь в окружающих его металлических массах. Вся энергия распространяется только внутри кабеля и более эффективно передается по цепи.

На рис. 4.17 изображены электромагнитные поля коаксиальной и симметричной цепей. Как видно из рисунка, электромагнитное поле коаксиальной цепи полностью замыкается внутри нее, а силовые линии электромагнитного поля симметричной цепи действуют на довольно значительном от нее расстоянии. Отсутствие внешнего электромагнитного поля обусловливает основные достоинства коаксиальных кабелей: широкий диапазон частот, большое число каналов, защищенность от помех и возможность организации однокабельной связи. В симметричных цепях из-за наличия внешнего электромагнитного поля возникают вихревые токи в соседних цепях и окружающих металлических массах (оболочка, экран), часть энергии рассеивается в виде потерь на тепло и увеличивается затухание. Кроме того, в симметричных кабелях за счет внешнего поля наводятся помехи в соседних цепях.

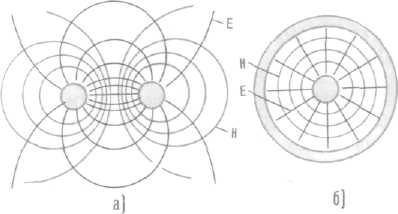
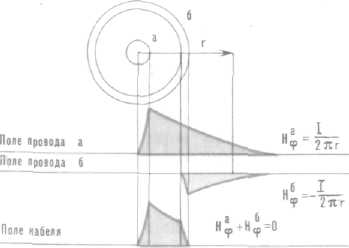
Рис. 4.16. Результирующее магнитное поле коаксиальной цепи и его составляющие

Рис. 4.17. Электромагнитное поле цепи: а) симметричной; б) коаксиальной

Рассмотрим действие поверхностного эффекта и эффекта близости в коаксиальных кабелях и определим характер распределения плотности токов в проводах при различных частотах.

Распределение плотности тока в проводе а определяется действием поверхностного эффекта (рис. 4.8). Перераспределение плотности тока по сечению проводника б обусловлено эффектом близости к нему проводника а.

На рис. 4.18 показано переменное магнитное поле, создаваемое током проводника а, которое наводит в металлической толще полого проводника б вихревые токи (/в.т)- На внутренней поверхности проводника б направления вихревых и основного токов совпадают (/ + /в.т), а на наружной поверхности они противоположны (/—/в.т). В результате ток в проводнике б перераспределяется так, что его плотность возрастает в направлении к внутренней поверхности.

Следовательно, токи в проводниках а и б коаксиальной цепи как бы смещаются и концентрируются на взаимно обращенных поверхностях проводников (рис. 4.19). Чем выше частота тока, тем сильнее эффект смещения тока на внешнюю поверхность проводника а и внутреннюю поверхность проводника б. Энергия как бы вытесняется из металлической толщи проводников и сосредоточивается внутри коаксиального кабеля, в изоляции , а проводники задают лишь направление распространению волн электромагнитной энергии.

Мешающее электромагнитное поле высокой частоты, создаваемое соседними цепями передачи или другими источниками помех, действуя на внешний проводник б (оболочку) коаксиальной цепи, распространяется не по всему сечению кабеля, а лишь по наружной его поверхности.

Таким образом, внешний проводник б коаксиального кабеля защищает (экранирует) передачу, ведущуюся по кабелю, мешающих влияний.

Рис. 4.18. Распределение плотности тока во внешнем проводнике

Из рис. 4.20 видно, что основной ток передачи (рабочий ток) концентрируется на внутренней поверхности проводника б коаксиального кабеля, ток помех — на наружной стороне этого проводника. Основной ток и ток помех проникают в толщу проводника лишь на глубину, определяемую коэффициентом вихревых токов. При этом чем выше частота, тем больше отдаляются друг от друга основной к и ток помех, и, следовательно, бель лучше защищен от действия сторонних помех. Таким образом, отличие от всех других типов кабелей в коаксиальных кабелях на высокиx частотах защита от помех обеспечивается их конструкцией.

Рис. 4.19. Концентрация токов на взаимно обращенных друг к другу поверхностях внутреннего (а) и внешнего (б) проводников коаксиальной цепи.

ПЕРВИЧНЫЕ ПАРАМЕТРЫ КОАКСИАЛЬНЫХ КАБЕЛЕЙ

В области высоких частот (свыше ) кГц), для которых используется коаксиальный кабель, первичные параметры могут быть определены по бедующим формулам. Активное сопротивление, Ом/км,

(4.40)

где k= — коэффициент вихревых токов; а—проводимость; rа и rb — радиусы внутреннего и внешнего проводников. Для медных проводников

Для алюминиевых проводников

Если внутренний проводник медный, а внешний алюминиевый,

Из приведенных формул следует, что при применении обоих алюминиевых проводников вместо медных сопротивление возрастает на 29%, а при замене меди на алюминий только у внешнего проводника сопротивление возрастает всего на 6%.

Индуктивность, Гн/км,

(4.41)

Для медных проводников

Для алюминиевых проводников

Если внутренний проводник медный, а внешний — алюминиевый,

В области высоких частот результирующая индуктивность определяется в основном внешней индуктивностью L = Lвш = 21n(rb/ra)10-4, поэтому замена меди на алюминий мало изменяет величину индуктивности кабельной цепи.

Емкость, нФ/км,

(4.42)

Здесь э — эффективное значение диэлектрической проницаемости.

Проводимость изоляции, См/км,

(4.43)

где tg 3 —тангенс угла диэлектрических потерь; Rиз — сопротивление изоляции, равное 10000 МОм-км. В области высоких частот, используемых для коаксиальных кабелей, величиной Go можно пренебречь и G = Ctg э.

Значения эффективной диэлектрической проницаемости еэ и тангенса угла диэлектрических потерь tg э комбинированной изоляции, применяемой в коаксиальных кабелях, приведены в табл. 4.5. Там же даны соотношения объемов диэлектрика Vд и воздуха Vв.

ОСОБЕННОСТИ РАСЧЕТА ВТОРИЧНЫХ ПАРАМЕТРОВ КОАКСИАЛЬНЫХ КАБЕЛЕЙ

Коаксиальные кабели практически используются в спектре от 60 кГц выше, где R< L и G< С, поэтом вторичные параметры можно рассчитывать по формулам:

коэффициент затухания, Нп/км,

коэффициент фазы, рад/км,

волновое сопротивление, Ом,

скорость распространения, км/с,

Однако эти параметры целесообразно выражать непосредственно через габаритные размеры (d и D) и xapaктеристики изоляции ( и tg ).

Коэффициент затухания а, дБ/км при подстановке в формулу = м + д первичных параметров и проведении соответствующих преобразований дл кабеля с медными проводниками определяется выражением

Из формулы видно, что потери в металлических элементах коаксиальной цепи (первый член) изменяются пропорционально f, а потери в изоляции (второй член) связаны с частоте линейным законом и с увеличение f возрастают значительно быстрее (рис. 4.21).

При использовании высококачественных изоляционных материалов (с малым

tg ) можно добиться определенном частотном диапазоне малых диэлектрических потерь и положить д = 0; при более высоких частотах они настолько возрастают, что причина д играет доминирующую роль в общем затухании кабеля, практически используемом спектре тот передачи по коаксиальным кабелям (до 60-106 Гц) при современных( изоляционных материалах величина д незначительна и затухание увеличивается примерно пропорционально f.

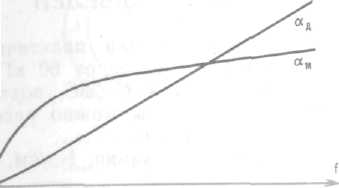
Рис. 4.21. Частотная зависимость составляющая затухания в металле (м) и в диэлектрике (д)

При замене медных проводников алюминиевые затухание возрастает пропорционально соотношению активных сопротивлений или соответственно обратно пропорционально корню квадратному из проводимостей металлов а/м =

, т. е. Затухания коаксиального кабеля с алюминиевыми проводниками больше, чем с медными на 29%.

При соотношении радиусов проводников rb/ra = 3,6 получим ---- = —— =

ам Ни

= 1,06, т. е. затухание кабеля возрастает всего на 6%. Изложенное дает основание сделать вывод о целесообразности применения коаксиальных кабелей с внешними алюминиевыми проводниками. При этом расход меди на изготовление коаксиального кабеля сокращается на 65%.

Коэффициент фазы , рад/км, коаксиальной цепи определяется из уравнения

Однако его можно выразить и таким образом:

(4.44)

где с — скорость света.

Скорость распространения v, км/с, электромагнитной энергии по коаксиальным цепям

(4.45)

коэффициент фазы с увеличением частоты возрастает прямолинейно. Это обусловливает почти полное постоянство скорости передачи энергии по коаксиальному кабелю во всем рассматриваемом спектре частот. Скорость передачи уменьшается с увеличением диэлектрической проницаемости е. Скорость передачи энергии по коаксиальным кабелям выше, чем по кабелям других типов, и приближается к скорости распространения электромагнитных волн в воздухе, т. е. к скорости света.

Волновое сопротивление ZB, Ом, коаксиальной цепи определяется по формуле

(4.46)

В кабелях со сплошной изоляцией ( = 2,3) ZB = 50 Ом, а в кабелях с комбинированной изоляцией ( = 1,1) волновое сопротивление составляет примерно 75 Ом.

Частотная зависимость волнового сопротивления в спектре от 60 кГц и выше весьма незначительна, и волновое сопротивление можно считать постоянной величиной.

PAGE 9

ЭЛЕКТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЦЕПЕЙ КАБЕЛЬНЫХ ЛИНИЙ СВЯЗИ