Алгоритм и программное обеспечение декодирования свёрточных турбокодов

С. А. Вартаньян

ФГУП «РНИИРС»

В современных системах передачи и обработки информации широко применяются турбокоды, как блочные, так и свёрточные. Популярность турбокодов вызвана их высокой исправляющей способностью.

Свёрточные турбокоды могут быть разделены на два класса: single binary и duo binary коды. Signal binary коды образованы над полем Галуа GF(2), при формировании кодовых слов на вход кодера поступает по одному биту данных. Duo binary коды образованы над полем Галуа GF(4), при формирование кодовых слов на вход кодера подаётся по два бита данных. Duo binary турбокоды приняты в качестве стандарта Европейским институтом стандартов по телекоммуникациям (ETSI), и всё шире применяются в современных системах связи.

В настоящее время существует достаточно много работ, посвящённых проблеме декодирования как блочных, так и свёрточных single binary турбокодов [1 – 4]. Однако работы, посвящённые декодированию duo binary турбокодов, практически отсутствуют. На рынке средств связи не представлены и программные продукты декодирования таких кодов, а аппаратные декодеры, например, микросхема TC1000 фирмы Turbo Concept (Франция), имеют ограниченное применение из-за высокой стоимости.

Рост популярности duo binary турбокодов, отсутствие доступных средств их декодирования определяет высокую актуальность разработки декодера duo binary свёрточных турбокодов.

В документах ETSI [5, 6] приведена укрупнённая структурная схема декодирования duo binary турбокодов. Исследования показали, что алгоритм, соответствующий данной структурной схеме, не является оптимальным с точки зрения вычислительной сложности.

Целью работы является разработка алгоритма и программного обеспечения декодирования duo binary турбокодов, обеспечивающих достаточную исправляющую способность и оптимизированных по количеству вычислительных операций.

В работе [7] описан обобщённый алгоритм декодирования single binary свёрточного турбокода. Представленная в [7] структурная схема, адаптирована автором для декодирования duo binary турбокодов. В результате чего разработан алгоритм декодера, обеспечивающий необходимую исправляющую способность и имеющий более низкую, чем алгоритм на основе структурной схемы, приведённой в [5, 6], вычислительную сложность, за счёт уменьшения количества операций перемежения, сложения и вычитания. Структурная схема этого декодера приведена на рисунке 1.

Уменьшение вычислительной сложности позволяет повысить быстродействие программного обеспечения декодирования сигналов, расширяет диапазон скоростей передачи сигналов, обрабатываемых «в реальном времени» программным способом, снижает требования к ресурсам, например, объем программируемых логических интегральных схем, при разработке аппаратных декодеров.

Рисунок 1. Декодер свёрточных турбокодов

Принцип работы рассматриваемого декодера основан на максимизации апостериорной вероятности входных символов, которая достигается максимизацией логарифмических отношений правдоподобия LLR. Максимизация LLR выполняется итерационно.

С выхода демодулятора на вход декодера поступает кодовый блок, представленный в виде «мягких решений» квадратурных каналов I и Q. Входные данные представлены в систематическом виде и являются сочетанием информационных символов и проверочных символов, передаваемых без перемежения и с перемежением (рисунок 2).

	Инф. символы	Проверочные символы без перемежения	Проверочные символы с перемежением
I	A0, A1, …, An-1	Y0,1, Y1,1, …, Yn-1,1	Y0,2, Y1,2, …, YN-1,2
Q	B0, B1, …, Bn-1	W0,1, W1,1, …, Wn-1,1	W0,2, W1,2, …, WN-1,2

Рисунок 2. Структура кодового блока на входе декодера

Для каждой части входного кодового блока формируется логарифмическое отношение правдоподобия по следующим формулам:

Для вычисления логарифмического отношения правдоподобия информационных символов LLR_I, проверочных символов без перемежения – LLR_С и проверочных символов с перемежением – LLR_СP используются соответствующие символы входного кодового блока:

;

Декодер образован последовательным соединением двух элементарных декодеров, так называемых декодеров с «мягким» входным и выходным сигналом (Soft-In Soft-Out – SISO). Каждый элементарный декодер имеет два входа: вход для LLR проверочных символов и вход для сигнала так называемой внешней информации, получаемой от другого элементарного декодера.

В ходе декодирования одного кодового блока значения LLR_C и LLR_CP не изменяются и на каждой итерации подаются соответственно на элементарные декодеры 1 и 2. Значение LLR_I на каждой из итераций корректируется. На каждой из итераций элементарный декодер 1 формирует оценку информационного символа LLR1, которая с учётом значения LLR2 и после перемежения поступает на вход элементарного декодера 2. Этот декодер формирует оценку LLR2 с учетом проверочных символов, переданных с перемежением.

На первой итерации значения Sum1 – Sum3 равны нулю.

Таким образом, на вход каждого из двух элементарных декодеров поступают LLR, результат декодирования на выходе элементарного декодера – также LLR.

Каждая последующая итерация увеличивает априорную информацию о переданном символе. Окончание процесса декодирования происходит или после выполнения заданного количества итераций, или после того, как величина вычисленного логарифмического отношения правдоподобия информационных символов LLR4 не изменяется от итерации к итерации.

Задачей элементарного декодера является максимизация LLR принятого символа. Для этого необходимо определить значения прямой метрики, обратной метрики и метрики перехода. Суть метрик рассмотрим по диаграмме переходов состояний регистров кодера, приведенной на рисунке 3.

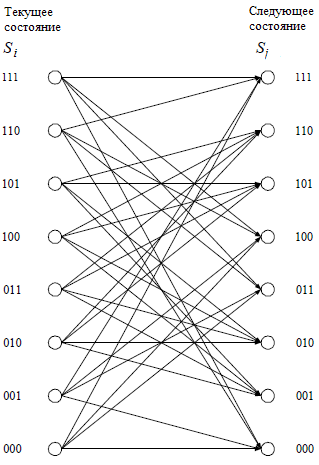
Рисунок 3. Диаграмма переходов состояний регистров кодера

Прямая метрика k(Si) – вероятность нахождения регистра сдвига кодера в одном из восьми возможных состояний в момент времени k. Обратная метрика k+1(Sj) – вероятность нахождения регистра сдвига кодера в одном из восьми возможных состояний в момент времени (k+1). Метрика перехода – вероятность перехода одного состояния регистра в другое для всех доступных переходов Метрики переходов из текущего состояния в последующее рассчитываются следующим образом:

При расчёте k(Si) и k+1(Sj) следует учитывать, что декодер принадлежит к классу декодеров с кольцевым обнулением, и начальное состояние заранее не известно. В связи с этим для определения начального состояния необходимо организовать итерационный процесс, учитывая, что начальное и конечное состояния одинаковы.

Для расчёта прямых метрик организуется итерационный процесс от момента времени k=0 к k=N. Если итерация не первая, то прямые метрики инициализируются значениями метрик в момент времени k=N, а иначе – нулём. Прямые метрики вычисляются следующим образом:

Далее производится нормировка полученных значений прямых метрик вычитанием метрики, соответствующей нулевому состоянию.

Для расчёта обратных метрик организуется итерационный процесс от момента времени k=N к k=0. Если итерация не первая, то обратные метрики инициализируются значениями метрик в момент времени k=0, а иначе – нулём. Обратные метрики считаются следующим образом:

Далее производится нормировка полученных значений обратных метрик вычитанием метрики, соответствующей нулевому состоянию.

На основе полученных метрик рассчитываются значения LLR выходных символов:

Перемежитель и деперемежитель реализованы в соответствии с алгоритмами, приведёнными в документах [5, 6].

В целом декодер, приведённый на рисунке 1, для каждого входного символа формирует соответствующие значения вероятностей, каждое из которых является вероятностью принятия одной комбинации пары бит. Декодер выбирает одну из комбинаций, соответствующих входному символу по критерию максимальности вероятности. Таким образом, комбинация, имеющая максимальную вероятность, будет являться откорректированным значением входного символа. Следовательно, если декодер исправляет ошибки в последовательности, то хотя бы для одной пары максимальное значение LLR окажется на другой позиции по сравнению с предыдущей итерацией. Поэтому в качестве критерия остановки итерационного процесса выбрана проверка на изменение позиции максимума.

Выходной формирователь «Ф» после окончания декодирования преобразует вероятностные решения в значения битов 0 или 1 . Для этого вычисляются логарифмы отношений правдоподобий для Ak и Bk на основе выходного отношения правдоподобий пары (Ak, Bk):

На основе приведённого алгоритма разработан программный декодер свёрточных турбокодов.

Результаты исследований показали, что исправляющая способность элементарного декодера мало зависит от количества итераций при расчёте прямых и обратных метрик. В связи с этим число итераций элементарного декодера при программной реализации выбрано равным двум. Однако исправляющая способность декодера существенно зависит от количества итераций декодера в целом. Установлено, что при скорости кодирования 2/3 при Eb/No порядка 3 дБ для обеспечения вероятности на выходе декодера порядка 10-7 требуется не более 4-х итераций. При этом на ПЭВМ с процессором Intel Core2 CPU 6600 «в реальном времени» выполняется декодирование фазоманипулированных сигналов, имеющих скорость манипуляции до 2,5 Мбод.

Результаты работы декодера приведены в виде графиков зависимостей вероятности ошибки (BER) на выходе декодера от отношения Eb/No (рисунки 4 – 8). На рисунке 9 приведён график BER от Eb/No, полученный из технического описания аппаратного декодера – микросхемы TC1000.

Как видно из приведённых зависимостей, декодер свёрточных турбокодов обеспечивает высокую исправляющую способность, сопоставимую с характеристиками декодера TC1000.

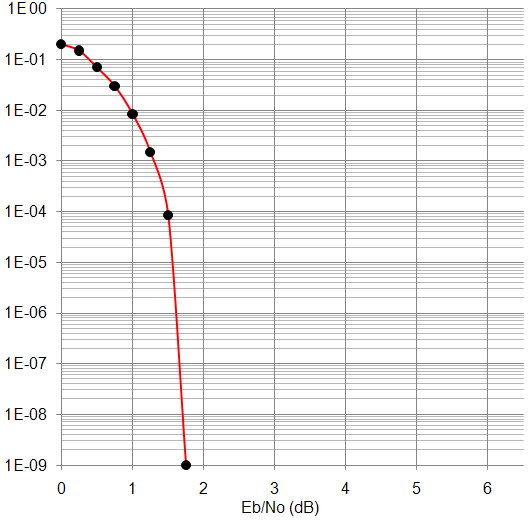
Рисунок 4. Рисунок 5.

Зависимость BER от Eb/No Зависимость BER от Eb/No

для N=228, R=1/3 для N=752, R=1/3

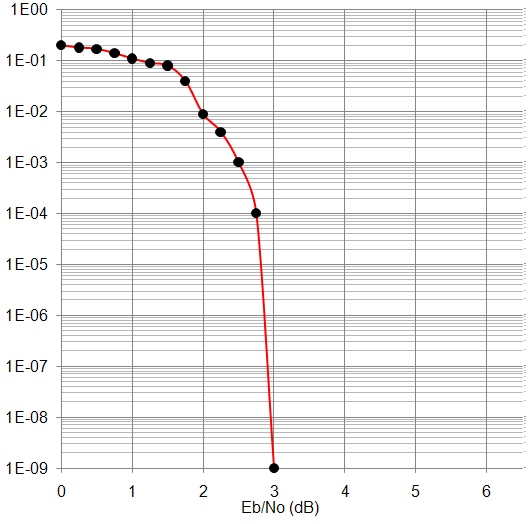
Рисунок 6. Рисунок 7.

Зависимость BER от Eb/No Зависимость BER от Eb/No

для N=228, R=2/3 для N=752, R=2/3

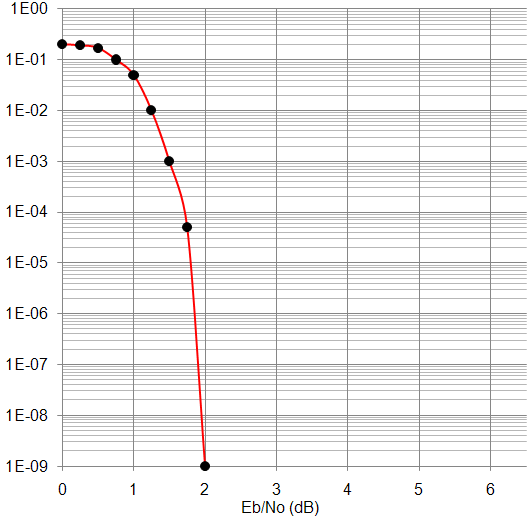
Рисунок 8. Рисунок 9.

Зависимость BER от Eb/No Зависимость BER от Eb/No

для N=432, R=1/2 для N=432, R=1/2 для TC1000

Заключение

Разработан алгоритм и программное обеспечение декодирования свёрточных турбокодов.

Представленный алгоритм декодирования свёрточных турбокодов обеспечивает сопоставимую с импортными аналогами исправляющую способность, оптимизирован по количеству вычислительных операций, что позволяет повысить быстродействие программного декодера, расширяет класс сигналов, обрабатываемых программным декодером в «реальном времени», снижает требования к ресурсам при аппаратной реализации.

Представленный алгоритм и программное обеспечение могут быть использованы для построения аппаратно-программных средств декодирования сигналов систем связи.

Литература

Питерсон У., Уэлдон Э. Коды, исправляющие ошибки.– М.: Мир, 1976. – 594 с.
Вартаньян С.А., Федоренко О.С., Стрыгин В.Н., Денисова Е.Ю., Подсухин Н.Л. Выбор значений коэффициентов обратной связи декодера блочных турбокодов, не зависящих от параметров турбокода. Общие вопросы радиоэлектроники. Научно-технический сборник. Вып. 1. 2008 г. С. 109 – 122
Near Optimum Error Correcting Coding And Decoding: Turbo-Codes. Claude Berrou, Alain Glavieux. IEEE Trans. on Comm. V. 44. NO 10. October 1996. P. 1261 – 1271.
Р. Морелос-Сарагоса. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. Москва: Техносфера. 2006. – 320 с.
Digital Video Broadcasting (DVB); Interaction channel for Satellite Distribution Systems; Guidelines for the use of ETSI EN 301 790. ETSI TR 101 790 V1.3.1 (2006-09).
Digital Video Broadcasting (DVB); Interaction channel for satellite distribution systems – ETSI EN 301 790 V1.4.1 (2005-09) European Standard (Telecommunications series).
Reflections on the Prize Paper: «Near optimum error-correcting coding and decoding: turbo codes». Claude Berrou and Alain Glavieux. IEEE Information Theory Society Newsletter. Vol. 48. No. 2. June. 1998. P. 23 – 31.

PAGE \* MERGEFORMAT 16

Алгоритм и программное обеспечение декодирования свёрточных турбокодов