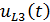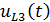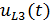Расчет переходных процессов в линейных электрических цепях
Одесский национальный политехнический университет
Кафедра теоретических основ и общей электротехники
КУРСОВАЯ РАБОТА
по курсу «Теория электрических и магнитных цепей»
по теме «Расчет переходных процессов в линейных электрических цепях»
Студента 2-го курса группы АТ-131
направления подготовки 6.050201 – «Системная инженерия»
специальности «Компьютеризированные системы и автоматика»
Кушнира Р.А.
Руководитель к.т.н., доц. Маевский Д.А.
Национальная шкала ______________________
Количество баллов: __________
Оценка: ECTS _____
Члены комиссии Маевский Д.А. _____________
(подпись)
Савёлова Э.В. _____________
(подпись)
Жеков О.П. _____________
(подпись)
Одеса 2014
Задание к работе
Схема электрической цепи для расчета переходного процесса приведена на рис. 1, параметры элементов — в таблице 1.
Таблица 1 — Параметры элементов цепи
|
R1, |
R2, |
R3, |
R4, |
L1, mH |
L3, mH |
Действие ключа |
Опре-делить |
|||
|
f, Hz |
Um, V |
, |
||||||||
|
8 |
10 |
6 |
10 |
32 |
48 |
50 |
120 |
-45 |
зам. |
|
Расчет переходного процесса
Напряжение изменяется по закону , либо в комплексной записи: .
Неизвестное напряжение запишем в виде суммы двух составляющих: свободной и принуждённой :
(1)
Принуждённую составляющую определим, рассчитав значение напряжения в установившемся режиме послекоммутационной схемы (рис.2), где резистор отсутствует.
В данном случае амплитудное значение напряжения в катушке будет равно:
(2)
Для поиска тока воспользуемся формулой разброса:
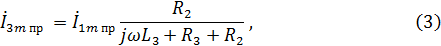
для которой найдём амплитудное значение тока по закону Ома:
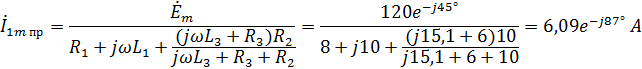
Подставив значение тока в формулу получим:
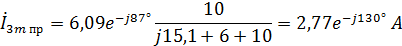
Теперь подставим значение тока в выражение :
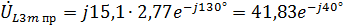
Запишем функцию времени для :
Для поиска свободной составляющей найдём её общий вид, который обусловлен корнями характеристического уравнения. Корни характеристического уравнения рассчитаем методом входного сопротивления. Для этого закоротим источник напряжения и в том же месте разорвём цепь (рис.3) для поиска входного сопротивления :
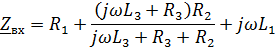
Приравняв правую часть к нулю, а к , получим характеристическое уравнение второго порядка (количество реактивных элементов — катушек — 2, то есть и порядок уравнения ):
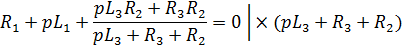
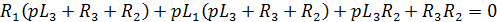
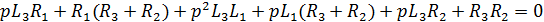
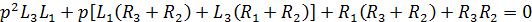
Подставляем действительные значения элементов и получим обыкновенное квадратное уравнение:
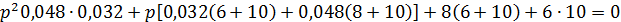
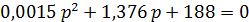
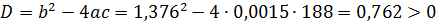
то есть корни будут иметь вид:
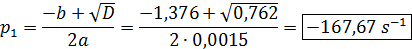
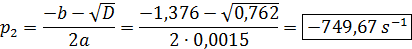
Имеем два корня, что говорит о том, что свободную составляющую будет представлена в следующем общем виде:
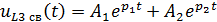
Постоянных две — и , поэтому составим систему уравнений, решив которую получим их численные значения:
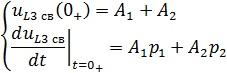
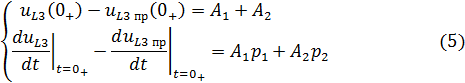
Из выражения получим :
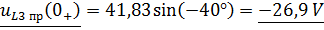
Продифференцировав то же выражение получим:
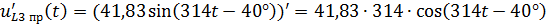
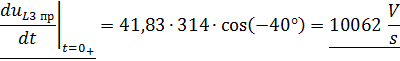
Воспользуемся первым и вторым законами Кирхгофа и составим систему уравнений для поиска нужных значений:
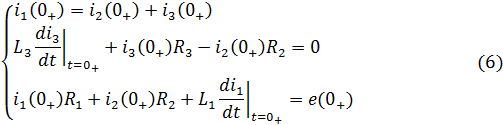
Найдём независимые начальные условия, для чего нам понадобится докоммутационная схема (рис.4).
Как и при поиске принужденной составляющей, найдём по закону Ома, а — по формуле разброса:
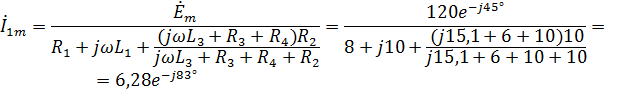
Отсюда функция от времени для будет иметь вид:
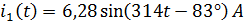
Получим первое начальное условие:

Формула разброса для :
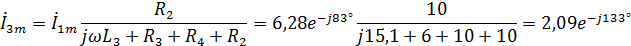
Отсюда функция от времени для будет иметь вид:
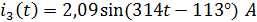
Получим второе начальное условие:
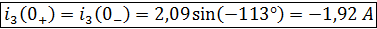
Из первого уравнения системы выразим :
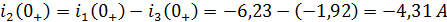
Обратимся ко второму уравнению системы и получим :
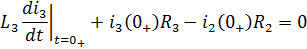
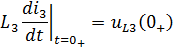
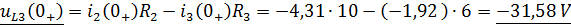
Продифференцировав то же выражение получим:
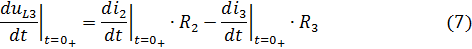
Производную третьего тока получим из второго уравнения системы:
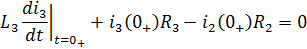
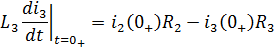
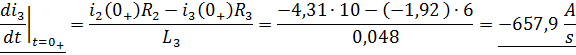
Производную первого тока найдём из третьего уравнения системы:
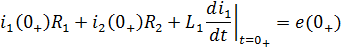
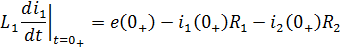
Значение источника напряжения в момент коммутации вычислим из начального закона изменения напряжения:
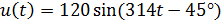
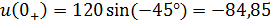
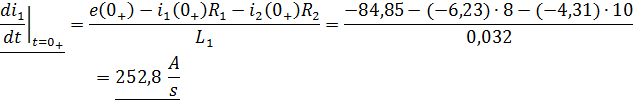
Производную второго тока найдём из первого уравнения системы, продифференцировав его: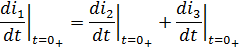
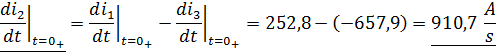
Подставим найденные значение в выражение :
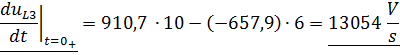
Возвращаемся к системе уравнений :
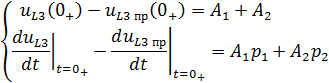

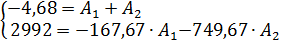
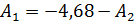
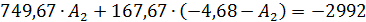
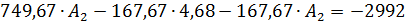
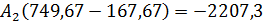
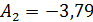
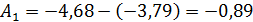
Итак, свободная составляющая имеет вид:
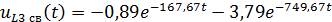
Можем теперь записать полный закон изменения напряжения на катушке по выражению :
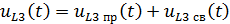
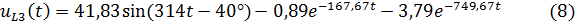
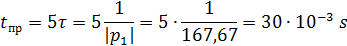
Построим график (рис.5) с помощью Microsoft Excel на основе таблицы значений для по формуле во временном диапазоне от 0 до 0,03:
Рис.1
EMBED Equation.3 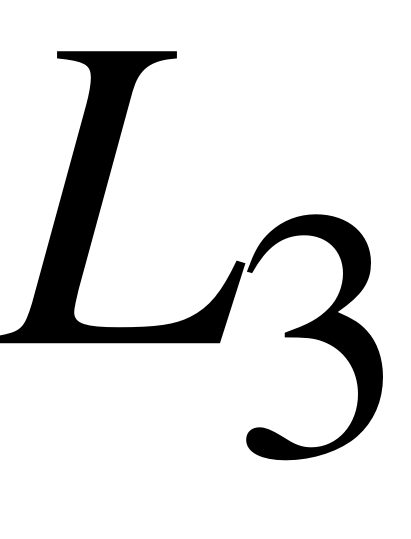
EMBED Equation.3 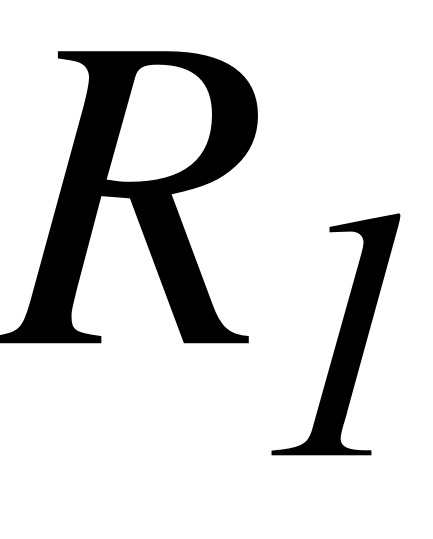
EMBED Equation.3 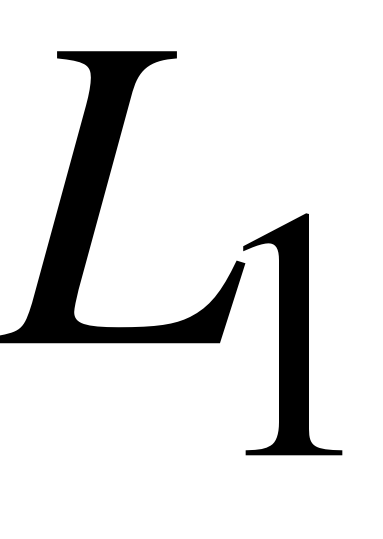
Рис.2 — Послекоммутационная схема
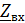
EMBED Equation.3 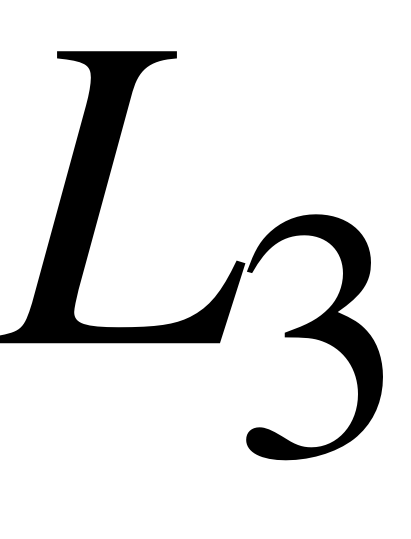
EMBED Equation.3 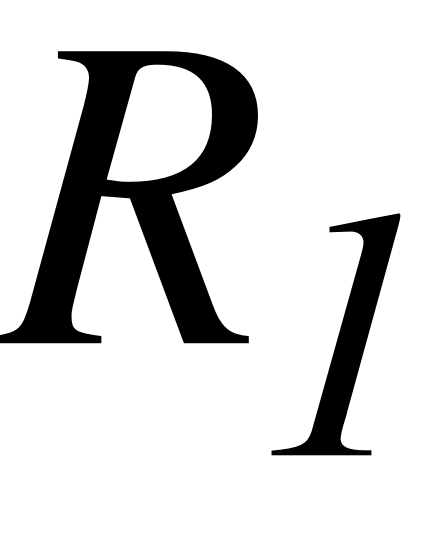
EMBED Equation.3 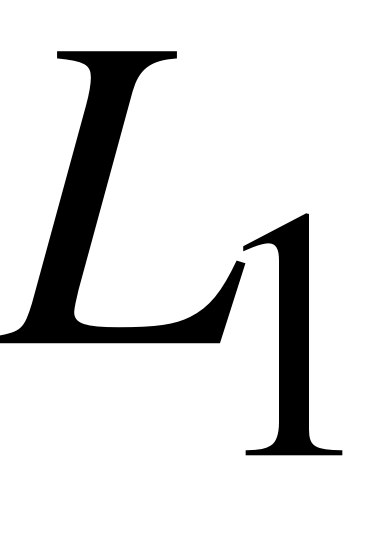
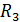
Рис.3
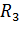
EMBED Equation.3 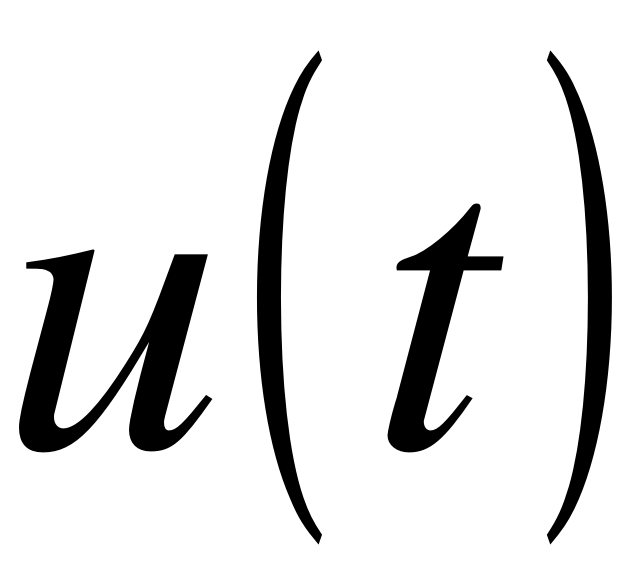
EMBED Equation.3 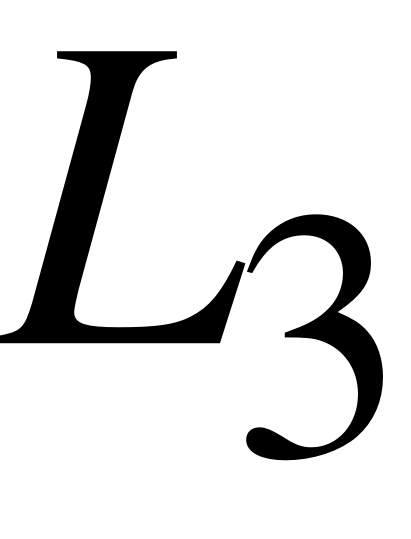
EMBED Equation.3 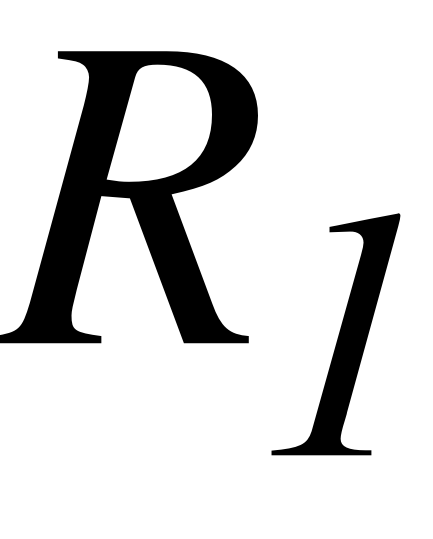
EMBED Equation.3 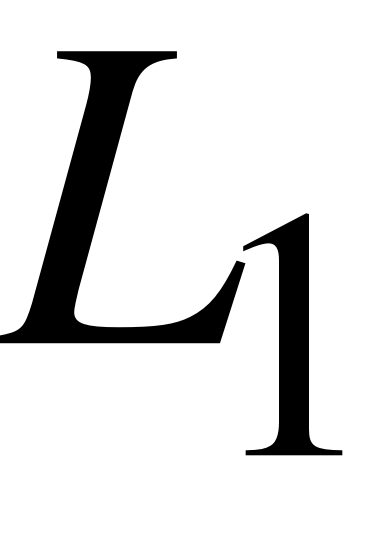
Рис.4 — Докоммутационная схема
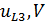
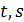
Рис.5 — График зависимости QUOTE