ВЫСОКОТЕМПЕРАТУРНАЯ ЯЧЕЙКА ДЛЯ ИМПЕДАНСНОЙ СПЕКТРОСКОПИИ КРИСТАЛЛОВ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
(ФГБОУ ВПО «КубГУ»)
Физико-технический факультет
Кафедра физики и информационных систем
Допустить к защите в ГАК
_____ . ____ . 2015 г.
Заведующий кафедрой
д-р физ.-мат. наук, профессор
_______________Н. М. Богатов
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА
БАКАЛАВРА
ВЫСОКОТЕМПЕРАТУРНАЯ ЯЧЕЙКА ДЛЯ ИМПЕДАНСНОЙ СПЕКТРОСКОПИИ КРИСТАЛЛОВ
Работу выполнил _____________________Зарецкий Александр Александрович
Направление 03.03.02 Физика (бакалавриат)
Научный руководитель
доцент ___________________________________________ Б. В. Игнатьев
Нормоконтролёр
канд. физ.-мат. наук, доцент _______________________ П. И. Быковский
Краснодар 2015
РЕФЕРАТ
Дипломная работа 51 с., 34 рис., 15 источников.
ИМПЕДАНСНАЯ СПЕКТРОСКОПИЯ, ГОДОГРАФ ИМПЕДАНСА, ЭКВИВАЛЕНТНАЯ СХЕМА ЗАМЕЩЕНИЯ, ВЫСОКОТЕМПЕРАТУРНАЯ ЯЧЕЙКА, СПЕКТРОСКОПИЯ КОМПОЗИТОВ.
Объектом разработки данной работы является высокотемпературная ячейка, предназначенная для проведения эксперимента по импедансной спектроскопии кристаллов.
Целью работы является проведение эксперимента по импедансной спектроскопии кристалла кремния, анализ полученных результатов и расчет на их основе такой характеристики материала, как диэлектрическая проницаемость среды.
В результате выполнения работы сконструирована высокотемпературная ячейка и вспомогательное устройство к прибору “ОСЦИГЕН”, выполнены необходимые измерения и расчеты. Также даны рекомендации по совершенствованию и оптимизации сконструированного оборудования.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Моделирование, синтез и исследование новых функциональных материалов является одним из актуальных научных направлений. Нередко новые материалы по характеру температурной зависимости сопротивления относят к полупроводникам. Однако в связи с возможным влиянием особенностей микроструктуры на транспорт носителей заряда такая формальная классификация может быть не вполне корректной и требует более детального рассмотрения. Вследствие сложного химического состава и микроструктуры функциональных материалов проблема оптимизации их параметров для прикладных целей также связана с определением механизмов переноса носителей заряда. Поэтому исследование электрофизических свойств полупроводников и полупроводниковых структур с учетом их реальной микроструктуры является важной и актуальной задачей.
Свойства разнообразных физических, физико-химических, электрохимических и многих других систем удобно изучать путем наблюдения за их откликом на слабое внешнее воздействие. Импедансный метод позволяет это сделать с высокой эффективностью. В последние десятилетия он утвердился в качестве одного из основных методов исследования электрохимических объектов. В сравнении с другими электрохимическими методами, этот метод обеспечивает наивысшую точность для исключительно широкого диапазона частот воздействующего сигнала и дает обширную информацию, как о кинетике электрохимических процессов, так и о свойствах поверхности и объема исследуемого объекта.
1 Теоретические данные
1.1 Векторные диаграммы токов
и напряжений. Треугольники сопротивлений и проводимостей
Импедансная спектроскопия гетерогенных систем основана на измерении и анализе зависимости комплексного электрического сопротивления Z (импеданса) от частоты переменного тока. С ее помощью можно определить структурные особенности ГС (распределение частиц электропроводящей фазы по объему диэлектрической матрицы, связь частиц в кластеры), микроскопические параметры (размеры кластеров, их локальное сопротивление) и другие характеристики ГС. Одним из этапов обработки результатов измерений ГС на переменном токе является построение и анализ эквивалентных схем (ЭС) замещения, т. е. электрических цепей, имеющих ту же зависимость импеданса от частоты, что и изучаемый образец ГС. Эквивалентные схемы состоят, как правило, из нескольких различных элементов: резисторов, конденсаторов, катушек индуктивности. Анализ ЭС и расчет их полного сопротивления сопряжен со сложением гармонических колебаний токов и напряжений. Рассмотрим некоторые особенности такого сложения. Если не оговаривается противное, то переменный ток считают квазистационарным. Это означает, что период колебаний тока много больше времени распространения электромагнитного поля в цепи (образце). Так как исследуемые нами гетерогенные (гетерофазные) системы представляют собой смесь, в которой частицы дисперсной фазы и/или их кластеры характеризуются некоторым размером, то целесообразно перейти от формулировки, основывающейся на понятии периода колебаний, к формулировке на языке длин электромагнитных волн. Тогда условие квазистационарности будет заключаться в превышении длины волны электромагнитного поля над размерами включений (кластеров и/или частиц) дисперсной фазы. Ограничимся также рассмотрением гармонических переменных токов, т. е. токов, величина которых меняется во времени по закону косинуса или синуса.
Гармонические колебания тока и напряжения можно изображать графически и производить их сложение с помощью векторных диаграмм. Возьмем произвольную прямую OX и вектор A, имеющий длину A и в начальный момент времени составляющий с прямой OX угол (рис. 1). Предположим, что этот вектор равномерно вращается против часовой стрелки с угловой скоростью , где- частота. Тогда угол между прямой OX и вектором A с течением времени изменяется по закону:
(1)
В соответствии с (1) проекции вектора A на ось OX и перпендикулярную ей ось OY изменяются по гармоническому закону:
(2)
(3)
Таким образом, при известной и постоянной угловой частоте (угловой скорости для вращающегося вектора) гармоническое колебание задается вектором A, имеющим длину A и повернутым в начальный момент времени на угол по отношению к оси абсцисс. Угол называют начальной фазой колебаний.
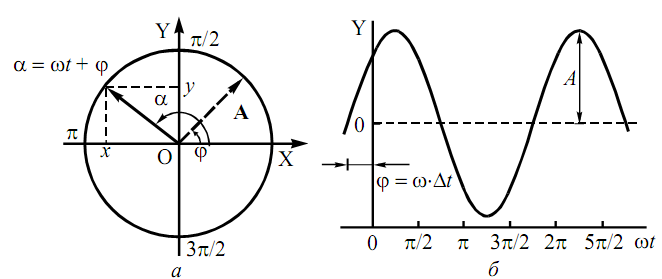
Рисунок 1 – Графическое изображение колебаний в виде вращения вектора(а); зависимость длины проекции вектора A на ось OY от времени(б)
Сложение гармонических колебаний, представленных векторами, может быть выполнено по правилу параллелограмма (рис. 2). Для этого строят вектор , изображающий первое колебание. Его длина равна амплитуде колебания, а угол между вектором и осью диаграммы определяет начальную фазу колебания. Далее строят вектор , соответствующий второму колебанию с амплитудой и начальной фазой . Угол представляет собой разность фаз двух колебаний. Проекции векторов и на ось диаграммы дают колебания: , ,. Сумма проекций двух векторов равна проекции суммы векторов. Поэтому вектор A представляет результирующее колебание с амплитудой A и начальной фазой .
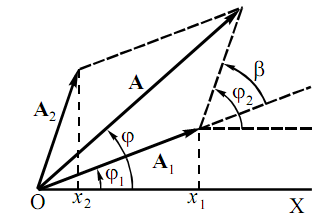
Рисунок 2 – Сложение колебаний при помощи векторов.
Рассмотрим несколько примеров электрических цепей (участков цепей). Для краткости элемент цепи (при исследовании образца - элемент эквивалентной схемы замещения) и численное значение физической величины, которой этот элемент обладает, будем обозначать одной и той же буквой.
1. Пусть цепь переменного тока (рис.3а) имеет только активное сопротивление (резистор с сопротивлением R). Сила тока I в цепи изменяется со временем по закону:
(4)
где - амплитуда силы тока, - угловая частота.
Тогда по закону Ома напряжение на активном сопротивлении стечением времени должно изменяться следующим образом:
(5)
Напряжение достигает своего максимального значения и обращается в ноль одновременно с током (рис. 3б), т. е. разность фаз между колебаниями тока и напряжения равна нулю.
Построение векторной диаграммы начинают с выбора направления оси токов (в общем случае произвольного). В соответствии с приведенными выше рассуждениями вектор напряжений на диаграмме строят по направлению оси токов, и его длина должна быть равной . Векторная диаграмма для активного сопротивления показана на рис. 4. Отметим, что векторные диаграммы в электротехнике обычно строят для действующих значений токов и напряжений. Принимая во внимание то, что в последующем у нас не будет необходимости в расчетах мощностей в цепях переменного тока, а также то, что амплитудные и действующие значения однозначно связаны друг с другом, мы ограничимся рассмотрением лишь амплитуд токов и напряжений.
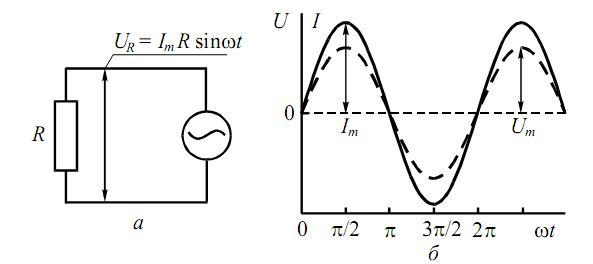
Рисунок 3 – Резистор (активное сопротивление) в цепи переменного тока (а); зависимости (б) тока и напряжения от времени.
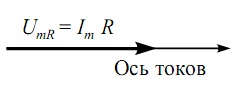
Рисунок 4 – Векторная диаграмма для резистора в цепи переменного тока.
2. Будем теперь считать, что в цепи переменного тока (рис. 5а) присутствует только конденсатор. Разность потенциалов на обкладках идеального (имеющего бесконечное сопротивление на постоянном токе) конденсатора определяется зарядом и его емкостью : .По определению сила тока в цепи равна заряду, протекающему в единицу времени:
(6)
Если сила тока в цепи изменяется по закону (4), то
(7)
Постоянную интегрирования , обозначающую заряд конденсатора, не связанный с колебаниями тока, можно считать равной нулю. Тогда напряжение на конденсаторе будет изменяться следующим образом (рис. 5б):
(8)
Сравнивая выражения (8) и (4), можно заметить, что синусоидальные колебания напряжения на конденсаторе отстают по фазе на /2 от колебаний тока. Когда сила тока в цепи равна нулю, конденсатор обладает максимальным зарядом и, следовательно, напряжение на нем максимально. Амплитуда колебаний напряжения на конденсаторе равна: . Если выполнить замену , то полученное выражение по форме совпадает с законом Ома для участка цепи на постоянном токе. Таким образом, величина является для амплитуд (или действующих значений) переменных токов и напряжений коэффициентом, аналогичным сопротивлению для постоянных токов в законе Ома. Говорят, что представляет собой реактивное сопротивление конденсатора.
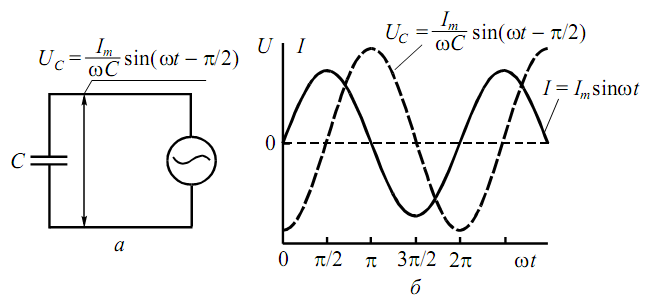
Рисунок 5 – Конденсатор (реактивное, емкостное сопротивление) в цепи переменного тока (а); зависимости (б) тока в цепи и напряжения на конденсаторе от времени.
Полученный результат можно представить в виде векторной диаграммы (рис. 6), на которой вектор, изображающий колебания напряжения, уже не совпадает (сравнить с рис. 4) по направлению с осью токов, а повернут относительно нее на угол -/2 (по часовой стрелке). Его длина равна амплитуде колебаний напряжения.
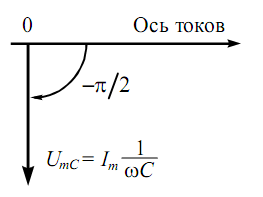
Рисунок 6 – Векторная диаграмма для конденсатора в цепи переменного тока
3. Рассмотрим катушку индуктивности в цепи переменного тока (рис. 7а). Будем считать, что активное сопротивление катушки пренебрежимо мало. Поэтому падение напряжения на катушке индуктивности определяется только ее эдс самоиндукции и равно:
(9)
где L – индуктивность катушки.
Если сила тока в цепи изменяется по закону (4), то напряжение на катушке индуктивности зависит от времени следующим образом:
(10)
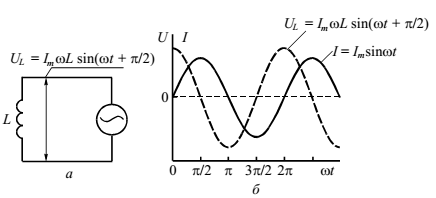
Рисунок 7 – Катушка индуктивности (реактивное, индуктивное сопротивление) в цепи переменного тока (а); зависимости (б) тока в цепи и напряжения на катушке индуктивности от времени
Из сравнения (10) и (4) следует, что колебания напряжения на катушке индуктивности опережают по фазе колебания тока на /2. Когда сила тока, возрастая, проходит через ноль, напряжение достигает максимума, после чего начинает уменьшаться. Когда же сила тока становится максимальной, напряжение проходит через ноль (см. рис.7б).
Векторная диаграмма для катушки индуктивности представлена на
рис. 8. Вектор, изображающий колебания напряжения, повернут относительно оси токов в положительном направлении (против часовой стрелки) на угол .
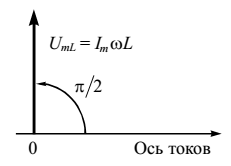
Рисунок 8 – Векторная диаграмма для катушки индуктивности в цепи переменного тока
Его длина равна амплитуде напряжения . Выполнив замену, можно получить выражение, по форме аналогичное закону Ома для участка цепи, в котором играет роль сопротивления.
Стоит отметить, что рассмотренные элементы цепи (резистор, конденсатор и катушка индуктивности) идеализированы. Это означает, что в резисторе происходит только необратимое преобразование электромагнитной энергии в тепловую, в конденсаторе - только накопление и возвращение источнику энергии электрического поля, а в катушке индуктивности - накопление и возвращение источнику энергии магнитного поля. И в конденсаторе, и в катушке индуктивности потери электрической энергии отсутствуют.
4. Применение метода векторных диаграмм для расчета сопротивления цепи переменного тока теперь можно проиллюстрировать на примере последовательно соединенных резистора, конденсатора и индуктивности (рис. 9). Пусть в цепи протекает переменный ток, задаваемый уравнением (4). Так как падение напряжения на соединенных последовательно элементах цепи равно сумме падений напряжения на каждом из них, то:, где ,, - мгновенные значения напряжения на конденсаторе, катушке индуктивности и резисторе.
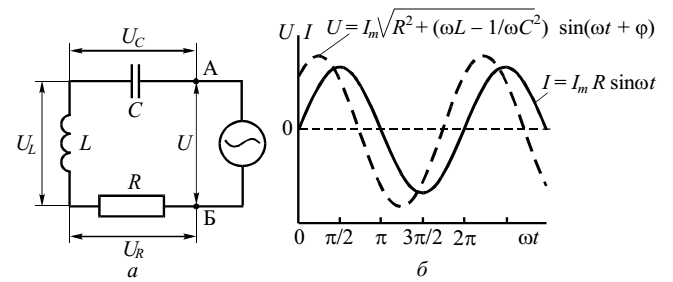
Рисунок 9 – Последовательное соединение конденсатора, катушки индуктивности и резистора (а); зависимости (б) тока в цепи и напряжения от времени
Следовательно, для того чтобы получить разность потенциалов в точках А и Б (напряжение U), необходимо сложить три гармонических колебания. Векторная диаграмма напряжений для цепи, показанной на рис. 9, приведена на рис. 10. Колебания напряжения на сопротивлении изображены на ней вектором , направленным вдоль оси токов и имеющим длину .
Векторы и , символизирующие колебания напряжения на индуктивности и емкости, направлены противоположно друг к другу и перпендикулярны к оси токов. Длины векторов и равны и соответственно.
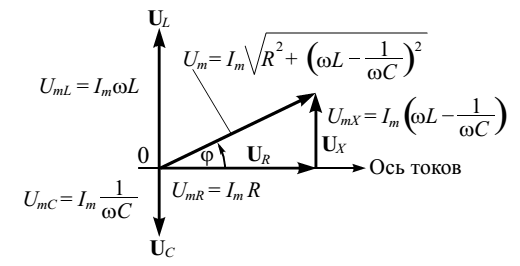
Рисунок 10 – Векторная диаграмма для последовательно соединенных конденсатора, катушки индуктивности и резистора
Выполнив сложение колебаний напряжения на индуктивности и емкости, можно упростить векторную диаграмму. На ней останутся лишь два вектора: - обозначает колебания, совпадающие по фазе с колебаниями тока (активная составляющая напряжения), и - обозначает колебания, отличающиеся по фазе на (реактивная составляющая напряжения). Будем считать, что, тогда вектор результирующего колебания повернут на угол против часовой стрелки относительно оси токов и его длина, как видно из рис. 10:
(11)
Цепь, показанная на рис. 9, не разветвлена, т. е. через все ее элементы протекает один и тот же ток. Поэтому, разделив (11) на амплитуду тока , получим выражение, определяющее модуль полного
сопротивления цепи переменного тока:
(12)
Активное и реактивное сопротивления, как и колебания напряжения, можно складывать геометрически. Соответствующий векторной диаграмме (рис. 10) треугольник сопротивлений приведен на рис. 2.11. Катеты R и X в треугольнике сопротивлений представляют собой активные и реактивные составляющие полного сопротивления Z. Присутствие активного сопротивления R в цепи переменного тока приводит к выделению теплоты по закону Джоуля - Ленца. Реактивное сопротивление:
(13)
не вызывает выделения теплоты, но определяет сдвиг фаз между током и напряжением. Из рис. 11 видно, что:
(14)
Из выражения (13) следует, что частотная зависимость реактивного сопротивления цепи из последовательно соединенных резистора, конденсатора и катушки индуктивности имеет особенность, а именно: при некоторой частоте переменного тока происходит смена знака . Частота называется резонансной. Выражение, связывающее с величинами емкости и индуктивности электрической цепи, определим, положив в (13) при . Тогда и
(15)
На рис. 12 представлена зависимость реактивного сопротивления последовательной RCL-цепи от угловой частоты .
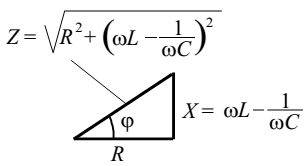
Рисунок 11 – Треугольник сопротивлений для последовательно соединенных конденсатора, катушки индуктивности и резистора
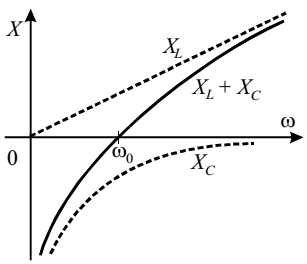
Рисунок 12 – Зависимость реактивного сопротивления X последовательной RCL-цепи от угловой частоты
Там же для сравнения показаны пунктирными линиями зависимости реактивного сопротивления конденсатора и катушки индуктивности . Следует особое внимание обратить на то, что при частотах цепь имеет такое же реактивное сопротивление, как и конденсатор с некоторой эквивалентной емкостью , меньшей емкости конденсатора, действительно включенного в цепь:
(16)
В свою очередь при эквивалентная индуктивность последовательной RCL-цепи меньше индуктивности L катушки:
(17)
Состояния резонанса ( = ) можно достичь, не только варьируя
частоту переменного тока, но и изменяя значения L и C. На этом принципе основывается работа специальных приборов - куметров, с помощью которых на переменном токе можно измерять сопротивления, емкости и индуктивности.
При резонансе () в последовательной RCL-цепи протекает ток
с амплитудой . Колебания напряжения на конденсаторе и ка-
тушке индуктивности находятся в противофазе, их амплитуды равны:
(18)
Как следует из (18), при напряжение на конденсаторе и катушке индуктивности может во много раз превышать напряжение питания. Величина имеет размерность сопротивления и называется характеристическим (волновым) сопротивлением колебательного контура. Отношение волнового сопротивления к активному определяет добротность колебательного контура
(19)
Отметим, что для описания прохождения переменного тока через цепь, содержащую резисторы, конденсаторы и катушки индуктивности, знания Z недостаточно. Необходимо знать величину сдвига фаз . Это становится понятно, если обратиться к рис. 10, 11 и вспомнить, что прямоугольный треугольник однозначно задается гипотенузой и углом между гипотенузой и катетом. Для того чтобы в одном выражении учитывать Z и , используют комплексные числа.
5. Рассмотрим цепь, состоящую из параллельно соединенных конденсатора, катушки индуктивности и сопротивления (рис. 13). От цепи источника отходят три ветви. Соответственно ток разделяется на три
Рисунок 13 – Параллельно соединенные конденсатор, катушка индуктивности и резистор
составляющие: ток конденсатора (мгновенное значение ), ток катушки индуктивности (), ток резистора (). При параллельном соединении элементов цепи складываются токи, протекающие через них:. Для того чтобы определить колебания тока в точках А и Б, построим векторную диаграмму (рис. 14). В отличие от предыдущего случая (схема на рис. 9 - последовательное соединение) в качестве исходной оси выберем ось напряжений и относительно ее отложим векторы, символизирующие колебания тока. На рис. 14 колебания тока на конденсаторе показаны вектором , повернутым относительно оси напряжений на угол +/2 (ток опережает напряжение - поворот против часовой стрелки). Длина вектора равна
(20)
Рисунок 14 – Векторная диаграмма для параллельно соединенных
конденсатора, катушки индуктивности и резистора.
Вектор , символизирующий колебания тока на индуктивности повернут на /2 в отрицательном направлении по отношению к оси напряжений (ток отстает от напряжения . поворот по часовой стрелке) и имеет длину
(21)
На участке активного сопротивления колебания тока совпадают по фазе с колебаниями напряжения, поэтому они изображаются вектором , направленным по оси напряжений и имеющим длину .
Рисунок 15 – Треугольник проводимостей для параллельно соединенных конденсатора, катушки индуктивности и резистора
Выполнив сложение колебаний тока на участках конденсатора и индуктивности, получим результирующие колебания реактивной оставляющей тока, изображенные на диаграмме вектором , перпендикулярным оси напряжений и имеющим длину
(22)
Колебания полного тока в точке А (или Б) определяются суммой векторов . Длина вектора I равна
(23)
Как следует из рис. 14, он повернут относительно оси напряжений на угол
(24)
Так как напряжение U одно и то же для всех параллельно соединенных элементов, то, разделив (23) на амплитуду колебаний напряжения , получим выражение, описывающее полную проводимость цепи, показанной на рис. 13. Соответствующий треугольник проводимостей приведен на рис. 15. Катеты треугольника представляют собой активную G и реактивную B составляющие проводимости:
(25)
(26)
Гипотенуза соответствует полной проводимости цепи (модулю адмиттанса):
(27)
Для адмиттанса, как и для импеданса, используют комплексную форму записи.
1.2 Представление импеданса и адмиттанса в виде комплексных чисел
Сложение колебаний тока и/или напряжения можно выполнять, представляя их в виде комплексных величин. Для этого используют формулу Эйлера:
(28)
где – аргумент, - мнимая единица. Из (28) следует, что любое комплексное число, записанное в алгебраической форме можно представить в показательной форме:
(29)
где и являются модулем и аргументом комплексного числа:
, (30)
Вещественная и мнимая части комплексного числа выражаются следующим образом:
, (31)
Вспомним рисунок 1. Угол между вращающимся вектором A и осью OX изменяется по закону:
(32)
а проекции A на оси абсцисс и ординат эквивалентны двум гармоническим колебаниям
(33)
(34)
происходящим с угловой частотой , имеющим амплитуду и начальную фазу .
Далее, используя (28)-(32), можно выразить колебания (33) и (34) при помощи одного комплексного числа:
(35)
Если частота одинакова для всех колебаний, рассматриваемых в каждой конкретной задаче, то в (35) множитель можно не использовать. Тогда гармонические колебания задаются выражением
(36)
которое называется комплексной амплитудой колебания. Ее модуль определяет фактическую амплитуду гармонического колебания, а аргумент - начальную фазу.
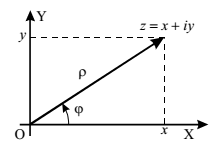
Рисунок 16 – Представление числа в виде вектора на комплексной плоскости
Представление колебаний с помощью комплексных чисел
согласуется с методом векторных диаграмм. Например, если
на плоскости ввести две взаимно перпендикулярные оси и по
одной из них (OX) откладывать действительную часть комплексного числа , а по другой (OY) – мнимую часть , то число будет изображаться на этой плоскости некоторым вектором (рис. 16). Длина этого вектора есть модуль комплексного числа , а угол между вектором и осью OX равен аргументу . Поэтому, задавая комплексную амплитуду (36), фактически определяют вектор, длина которого равна амплитуде колебаний, а угол поворота - начальной фазе, т. е. поступают так же, как описано в предыдущем параграфе. Различие (и преимущество) состоит только в компактной форме записи колебаний.
Вернемся к схеме, представленной на рис. 3а, и рассмотрим ее, используя представление токов, напряжений, сопротивлений и проводимостей в виде комплексных величин. Определим комплексные выражения для колебаний тока (4) и напряжения (5) на сопротивлении:
(37)
(38)
Комплексная амплитуда колебания напряжения в данном случае не содержит мнимой части, т. к. при отсутствии сдвига фаз () между колебаниями тока и напряжения .
Для простейшей цепи с конденсатором (см. рис. 5) колебания напряжения на конденсаторе отстают по фазе от колебаний тока на . Выражение (8) в комплексной форме выглядит следующим образом:
(39)
Комплексная амплитуда колебаний напряжения на конденсаторе равна
(40)
Множитель на комплексной плоскости изображается вектором, имеющим единичную длину и направленным против оси OY. Воспользовавшись формулой Эйлера (28) и тем, что , выражение (40) можно записать следующим образом:
(41)
Колебания напряжения на индуктивности (см. схему на рис. 7а) опережают по фазе колебания тока на /2. Поэтому выражение (10) может быть определено так:
(42)
Комплексная амплитуда этих колебаний равна:
(43)
Аналогично (41) имеем:
(44)
Для сложения нескольких колебаний одинаковой частоты достаточно сложить комплексные амплитуды этих колебаний. Модуль полученного комплексного числа дает фактическую амплитуду результирующего колебания, а его аргумент - начальную фазу. Соответственно, на комплексной плоскости сложение колебаний представляется сложением векторов.
Согласно (38)-(44) для последовательно соединенных резистора, конденсатора и катушки индуктивности (см. рис. 9) сложение колебаний напряжения в точках А и Б в форме комплексных амплитуд будет выглядеть следующим образом:
(45)
где и - действительная и мнимая составляющие комплексной величины .
По правилам (30) получаем выражение для амплитуды и начальной фазы напряжения в точках А и Б:
(46)
(47)
что совпадает с (11) и (14).
Введя понятие комплексного сопротивления (импеданса) как величины, представляющей собой отношение комплексной амплитуды напряжения к комплексной амплитуде силы тока , выражение (45) можно переписать следующим образом:
(48)
При записи (48), как и при записи (39)-(46), считаем, что по (4) и (37) комплексная амплитуда колебаний тока в цепи последовательно соединенных элементов не содержит мнимой части.
Согласно (48) комплексное сопротивление имеет действительную и мнимую части:
(49)
(50)
(51)
Модуль комплексной величины (импеданса) есть полное сопротивление:
(52)
Рассмотрев схему, приведенную на рис. 13, можно записать выражение для сложения колебаний тока в точке А (или Б) в комплексной форме:
(53)
В таком случае выражение
(54)
описывает комплексную проводимость (адмиттанс) схемы, приведенной на рис. 13. Так же, как и импеданс, адмиттанс содержит действительную Y и мнимую Y части:
(54)
(55)
(56)
Модуль адмиттанса представляет собой полную проводимость цепи
(57)
При исследовании гетерогенных систем достаточно часто измеряются не действительная и мнимая части импеданса , а его модуль и угол сдвига фаз между колебаниями тока и напряжения. Согласно (31) переход от и к действительным и мнимым частям импеданса (адмиттанса) осуществляется следующим образом:
, (58)
, (59)
Простейшие электрические цепи переменного тока, составленные из резистора, конденсатора и катушки индуктивности, приведены в соответствующей литературе. Так как импеданс (адмиттанс) является комплексной величиной, то допускается векторное представление. Поэтому рядом с каждой схемой цепи показана векторная диаграмма импеданса (адмиттанса). Приведены также амплитудночастотные и фазочастотные характеристики схем, т. е. зависимости от угловой частоты модуля импеданса Z и угла сдвига фаз между колебаниями тока и напряжения. В таблице представляет собой резонансную частоту, на которой равны друг другу индуктивная и емкостная составляющие импеданса (адмиттанса).
2 Применение эквивалентных схем замещения
Данные, полученные при измерении гетерогенных систем на переменном токе, могут быть записаны в виде частотных зависимостей импеданса, адмиттанса и комплексной емкости, определяемой как (комплексной диэлектрической проницаемости: , где и - действительная и мнимая части , - емкость конденсатора, имеющего те же геометрические параметры, что и исследуемый, но заполненного вакуумом), и комплексного электрического модуля , где и - действительная и мнимая части комплексного электрического модуля.
Конкретный вид представления экспериментальных результатов выбирается, исходя из требований удобства их последующего анализа и однозначности интерпретации. Для определенности в разделе 2
будет использоваться понятие импеданса. Однако следует иметь в виду,
что аналогичные рассуждения и выводы справедливы и для других
комплексных величин.
Анализ зависимости можно выполнять различными способами. Основным и самым наглядным является построение эквивалентных схем (ЭС) замещения. Под эквивалентной схемой замещения понимают модельную электрическую схему, составленную из идеализированных резисторов, конденсаторов, катушек индуктивности и имеющую ту же зависимость импеданса от частоты, что и исследуемый образец (в пределе одной заданной частоты - то же значение импеданса). Вид эквивалентной схемы замещения будет определяться не только свойствами гетерогенной системы, но и диапазоном частот, в котором образец исследуется. При его расширении в эквивалентную схему могут добавляться новые элементы, уточняющие и дополняющие ЭС.
Простейшим методическим приемом определения эквивалентной схемы замещения является последовательное применение различных представлений. На каждом этапе анализа рассматривают простейшую (например, двухэлементную - резистор и конденсатор) схему замещения. Определив численное значение емкости или сопротивления какого-либо из элементов, его исключают из общего измеренного импеданса (адмиттанса и т. д.) и затем преобразуют остаток в следующую схему (представление). Так поступают до тех пор, пока не будут выяснены все параметры многокомпонентной эквивалентной схемы замещения.
Обычно измерения частотных зависимостей импеданса выполняют в интервале частот от единиц Гц до десятков МГц. В случае необходимости используют несколько специализированных приборов и расширяют диапазон в сторону низких частот до сотых долей Гц, в сторону высоких - до десятков ГГц. В общем случае, чем шире частотный диапазон, тем точнее можно составить эквивалентную схему замещения. Следует иметь в виду, что удачный выбор ЭС предполагает не только совпадение зависимостей исследуемого образца и эквивалентной схемы замещения, но и согласованность ЭС с физической моделью исследуемой системы, а также с целью исследования. Поэтому уточнение ЭС путем добавления новых элементов не является самоцелью. В ряде случаев необходимо ограничиться эквивалентной схемой более простой (содержащей меньшее число элементов), но зато полнее соответствующей физической модели объекта. Возможные в таком случае отклонения в частотных зависимостях импеданса ГС и эквивалентной схемы устраняют, вводя, например, как в случае электрохимических ячеек, дополнительные (по сравнению с обычными компонентами электрической цепи) элементы ЭС. Это полезно в тех случаях, когда частотная зависимость импеданса образца ГС описывается относительно несложными уравнениями с небольшим числом параметров, а представление их в виде резисторов конденсаторов и индуктивностей потребовало бы использования сложной ЭС. Типичными элементами эквивалентных схем такого рода являются элемент постоянной фазы и элемент Варбурга, широко используемые при анализе электрохимических ячеек.
Частотные зависимости импеданса определяются многими физическими причинами, причем некоторые из них проявляются при одних и тех же частотах. Перечислим несколько основных факторов, влияющих на зависимость .
- Электронные релаксационные процессы на границах раздела фаз.
Отличие значений удельной электропроводности и диэлектрической
проницаемости фаз, составляющих систему, приводит к поляризации
Максвелла-Вагнера, которая характеризуется определенным временем релаксации, что проявляется в виде дисперсии импеданса.
- Дисперсия электрических характеристик (удельной электропроводности и диэлектрической проницаемости) фаз, входящих в систему. Например, прыжковая электропроводность зависит от частоты переменного тока. Поэтому если в одной из фаз композита возможен прыжковый перенос заряда, то импеданс материала будет зависеть от частоты.
- Релаксационные процессы на границах раздела фаз, связанные с переносом ионов и электрохимическими реакциями. Диффузия и электрохимические реакции происходят с конечной скоростью, что приводит к временной зависимости приэлектродных процессов и появлению частотной дисперсии импеданса.
- Наличие структурных (имеющих определенную геометрию) элементов с реактивным импедансом. Импеданс идеального конденсатора зависит от частоты . Поэтому даже в случае отсутствия
дисперсии электрических параметров фаз, составляющих гетерогенную систему, для образцов с различной геометрией распределения компонент гетерогенной системы по ее объему будут наблюдаться разные частотные зависимости импеданса.
Сложность зависимостей для гетерогенной системы, с одной стороны, требует тщательного анализа спектров импеданса, с другой – обусловливает большую информативность импедансной спектроскопии. Выполнение измерений на различных частотах, построение эквивалентных схем замещения во всем исследуемом интервале частот и в выделенных диапазонах, в которых максимально проявляются одни факторы и минимизированы другие, а также сравнение эквивалентных схем замещения с физической моделью гетерогенной системы позволяет разграничить влияние многочисленных факторов на Z и получить необходимую экспериментатору информацию. Есть случаи, когда интерес представляет какое-либо одно свойство системы. Например, интересует зависимость от частоты прыжковой электропроводности “металлической” фазы, можно ограничиться меньшим диапазоном частот, в котором именно этот механизм определяет ход . Иными словами, при наличии дополнительных сведений, полученных в ходе предварительных измерений образца на переменном токе, либо при помощи других экспериментальных методик (электронная, туннельная микроскопия, электронный парамагнитный резонанс и т. п.), частотный диапазон можно существенно ограничить.
Используя импедансную спектроскопию, нужно иметь в виду, что отдельно взятый спектр импеданса трудно интерпретировать однозначно, даже на уровне поиска эквивалентной схемы (спектры совершенно разных электрических цепей могут быть очень похожими). Дополнительную информацию для уточнения эквивалентных схем замещения и анализа ГС можно получить, проводя измерения частотных зависимостей Z в различных условиях. Например, при разных температурах или при дополнительном наложении внешней электрической разности потенциалов. При этом изменяются вклады разных факторов в полный отклик системы на воздействие переменным током, что позволяет, во-первых, более надежно определить тип эквивалентной схемы, во-вторых, проследить за изменением каждой из составляющих отклика, связанной с определенным элементом эквивалентной схемы. Особенно продуктивен такой подход при изучении электрохимических реакций в тонком приэлектродном слое и продуктов таких реакций.
Составить наглядное представление о поведении частотной зависимости Z можно, построив его годограф. Под годографом будем понимать траекторию, описываемую на комплексной плоскости вектором Z. В качестве примера рассмотрим далее несколько простейших эквивалентных схем замещения, составленных из резисторов и конденсаторов, и построим годографы их импеданса.
2.1 Паралелльная RC-схема замещения
Так как в ходе выполенения эксперимента по данной работе я ограничился паралелльной RC-цепочкой замещения для описания образца, то ниже приведен теоретический расчёт только для неё. Расчёт других простейших и более сложных эквивалентных схем можно найти в литературе, представленной в списке литературы.
При параллельном соединении элементов электрической цепи их проводимости складываются. Поэтому при известных сопротивлении резистора и емкости конденсатора для RC-цепи, изображенной на рис. 17, складываются обратные величины активного и реактивного (емкостного) сопротивлений и рассчитывается адмиттанс:
(60)
где – действительная часть адмиттанса, – мнимая часть адмиттанса, - сопротивление резистора, - емкость конденсатора.
Откладывая в комплексной плоскости значения действительной и мнимой частей для каждой частоты, можно построить годограф адмиттанса (рис. 18).
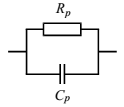
Рисуонк 17 – Паралелльная RC-цепочка
Он представляет собой параллельный оси луч,
выходящий из точки на оси .
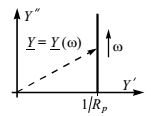
Рисунок 18 – Годограф адмиттанса паралелльной RC-цепочки
Выписав отдельно выражения для действительной и мнимой частей импеданса
(61)
(62)
можно заметить, что они связаны друг с другом простым соотношением:
(63)
Используя формулу (63) в виде , можно из формулы (61) исключить угловую частоту :
(64)
Перенеся все величины в левую часть, получим равенство , которое после домножения обеих частей на принимает вид
(65)
Можно заметить, что выражение (65) является уравнением окружности в декартовых координатах. Для того чтобы привести его к стандартному виду, перепишем (65) следующим образом:
(67)
Первые три члена в (67) образуют квадрат разности (), тогда
(68)
что представляет собой уравнение окружности в координатах Z - Z . Физический смысл имеет только полуокружность, показанная на рис. 19 (годограф импеданса). Ее радиус равен , а центр расположен на оси
Z на расстоянии от начала координат. Если частота переменного
тока увеличивается (в пределе ), то импеданс параллельной RC-
цепи (рис. 17) стремится к нулю, т. е. конденсатор шунтирует резистор.
При нулевой частоте импеданс конденсатора бесконечно велик, весь ток
протекает через резистор и, соответственно,.
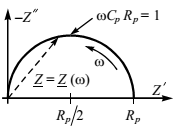
Рисунок 19 – Годограф импеданса параллельной схемы замещения
3 Описание необходимого для эксперимента оборудования
3.1 Высокотемпературная ячейка и источник питания
В ходе проведенного мною эксперимента измерялся импеданс пластинки кремния толщиной 0.3 мм и радиусом 23 мм. Для генерации в нем носителей заряда было решено нагревать образец и проводить измерения при различных температурах.
Для этого была создана высокотемпературная ячейка. Она представляет собой две последовательно соединенные групы из четырех паралелльно соединенных резисторов. Номинал каждого резистора – 56 Ом, рассеиваемая мощность – 10 Ватт.
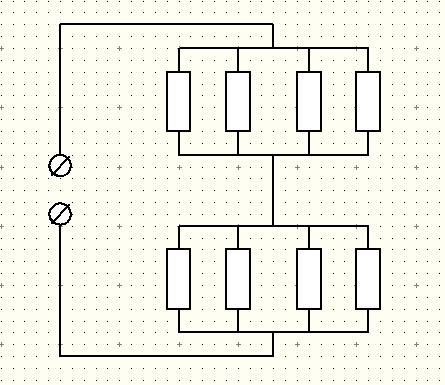
Рисунок 20 – Электрическая схема высокотемпературной ячейки
Каждая группа резисторов закреплена на керамической подставке. Соединены группы резисторов термостойким проводом во фторопластовой оболочке. Сверху на резисторы наклеены медные пластинки-электроды, к которым в свою очередь припаяны провода для измерения импеданса. В ходе лабораторных измерений выяснилось, что максимально допустимая температура нагрева ячейки составляет примерно , что обусловливается температурой плавления припоя, с помощью которого соединены детали. Для проведения эксперимента по импедансной спектроскопии этой температуры достаточно.

Рисунок 21 – Высокотемпературная ячейка для импедансной спектроскопии.
Источником питания высокотемпературной ячейки является тиристорный регулятор переменного тока, который я сделал в качестве курсовой работы в 2013-2014 учебном году.
Тиристорный регулятор переменного тока выполнен на основе двух тиристоров Т112-16-12, включенных встречно-паралелльно и микросхемы К1182ПМ1, которая является фазовым регулятором. Схема достаточно проста. К сети переменного тока (220 В) последовательно подключается предохранитель на 8 А, нагрузка, и 2 тиристора Т112-16-12, включенные встречно параллельно. Для того чтобы через цепи управления каждого из тиристоров, в нерабочий полупериод, не протекал ток управления, используется развязка из диодов КД411ВМ. Это гарантирует правильную работу тиристоров во время рабочего полупериода сетевого напряжения.
Резистор 600 Ом используется для ограничения тока управления. А при помощи регулировочного резистора 68 кОм меняется мощность, отдаваемая в нагрузку. Конденсатор на 100 мкф используется для плавного пуска, конденсаторы на 5 мкф используются для обеспечения требуемой задержки включения тиристоров на каждой полуволне сетевого напряжения относительно нуля фазы напряжения, приложенного к микросхеме. Эти конденсаторы также гарантируют закрытое состояние тиристоров в момент включения микросхемы в сеть.
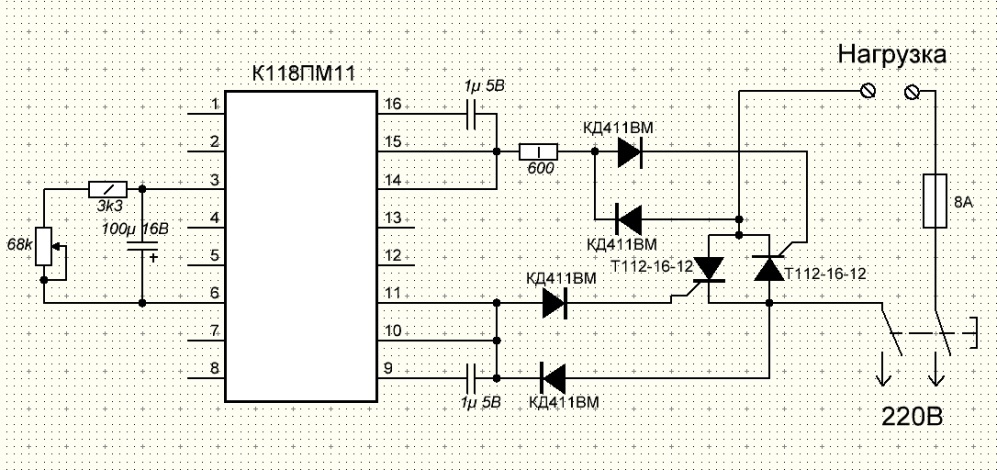
Рисунок 22 – Электрическая схема тиристорного регулятора.
Принцип работы устройства можно понять из нижеследующего рисунка. Для регулировки мощности изменяется угол открытия тиристоров. Чем больше угол , тем меньшая часть синусоиды пропускается в нагрузку. Когда оба тиристора полностью закрыты и мощность в нагрузку не передаётся. Когда в нагрузку поступает вся синусоида полностью и соответственно передаётся полная мощность. В первый момент после включения нагрузки угол всегда равен . Далее он начинает плавно уменьшаться до значения соответствующего текущему положению регулировочного резистора. За счёт этого и достигается плавный пуск.
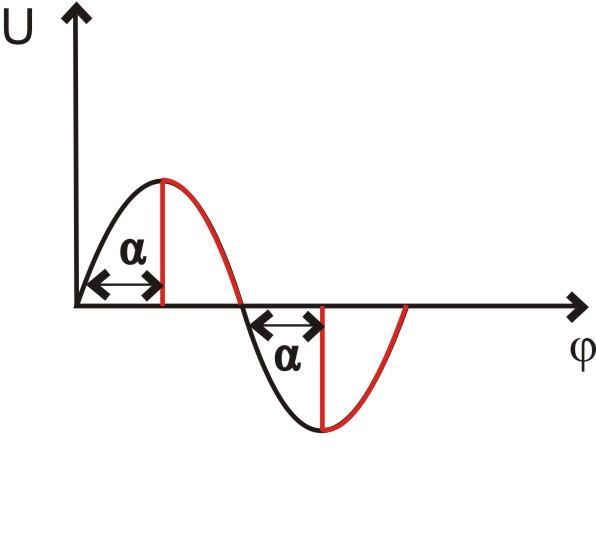
Рисунок 23 – Принцип работы тиристорного регулятора.
3.2 Прибор ”ОСЦИГЕН” и вспомогательное устройство
Для непосредственного измерения импеданса образца используется прибор ”ОСЦИГЕН”. Виртуальный прибор ”ОСЦИГЕН” (осциллограф-генератор) предназначен для использования совместно с персональным компьютером и представляет собой конструкцию на основе программируемой логической интегральной схемы (ПЛИС фирмы Altera), конфигурацию которой можно оперативно менять в зависимости от вида измерений. Прибор может быть использован как двухканальный осциллограф и двухканальный функциональный генератор (стандартная конфигурация), как регистратор сигнала фотоэлектронного умножителя в токовом режиме и в режиме счета одноэлектронных импульсов. Возможно использование прибора ”ОСЦИГЕН” в спектроскопии ядерного магнитного и квадрупольного резонансов.
В данной работе прибор ”ОСЦИГЕН” использовался для импедансной спектроскопии кристалла кремния. Прибор ”ОСЦИГЕН” позволяет производить измерения при широком диапазоне частот и при различных температурах, что позволяет исследовать объемные и поверхностные электрические свойства монокристаллов.
Схема измерений представлена на рисунке 24. Синтезированный методом прямого цифрового синтеза синусоидальный сигнал частотой через выход C прибора ”ОСЦИГЕН” подается через активное сопротивление на комплексное сопротивление . Через вход A с использованием переключателя 10 поочередно измеряются комплексные напряжения и как функции частоты . Модуль и фаза напряжений и определяются с помощью квадратурного детектора на элементах 5 – 8 по формулам:
(69)
(70)
Далее определяется комплексный коэффициент передачи:
(71)
Коэффициент передачи может быть так же определен по формуле:
(72)
Далее через коэффициент передачи выражается значение импеданса:
(73)
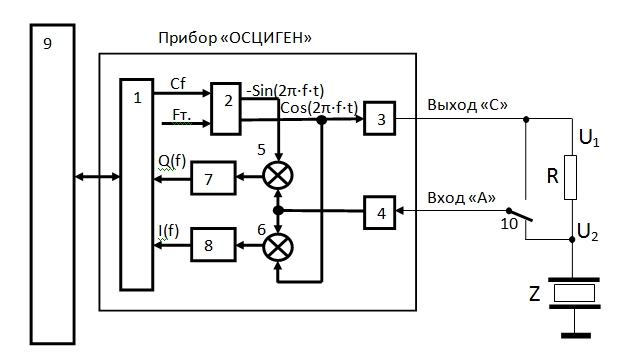
Рисунок 24 – Схема прибора ”ОСЦИГЕН”. 1 – интерфейс; 2 – блок прямого цифрового синтеза частоты; 3 – цифро-аналоговый преобразователь; 4 – аналого-цифровой преобразователь; 5,6 – цифровые умножители; 7,8 – цифровые фильтры низких частот; 9 – компьютер; 10�� ��– переключатель; R – активное сопротивление; Z – измеряемое комплексное сопротивление; Fт. – тактовая частота (50 – 100 МГц); частота f < Fт./2; f=Cf· Fт./232;
Cf – код частоты.
Для автоматизации и повышения точности измерения импеданса, в дополнение к прибору ”ОСЦИГЕН” было сконструировано вспомогательное устройство. Его схема представлена на рисунке 25.
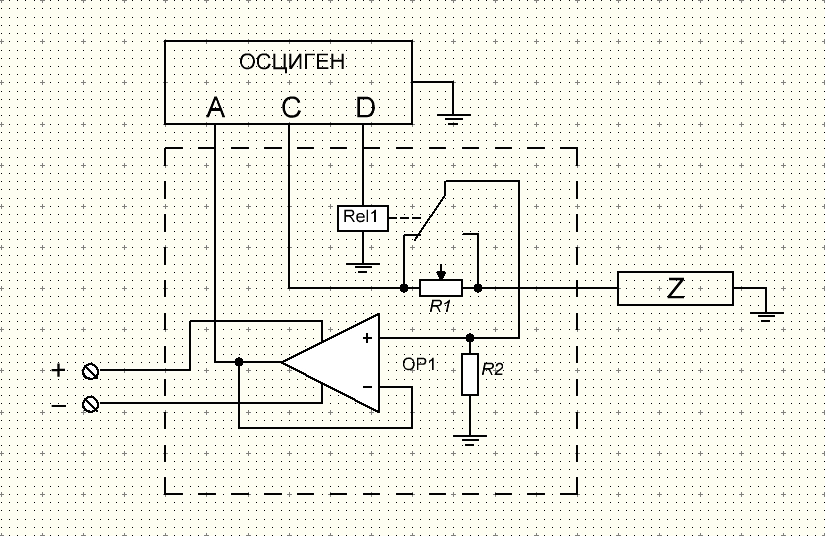
Рисунок 25 – вспомогательное устройство к прибору ”ОСЦИГЕН”.
Устройство выполнено в экранированном корпусе. Устройство имеет 3 три разъёма – для выводов A, C и D прибора ”ОСЦИГЕН”. Через разъем С подается синусоидальный сигнал на образец. Активное сопротивление , через которое подается синусоидальный сигнал, сделано переменным для более точной подстройки диапазона измерения. На канале А установлен операционный усилитель для снижения входной емкости прибора ”ОСЦИГЕН” и подтягивающий резистор. Канал D используется для включения и выключения реле, которое переключает ключ, соединенный с каналом А, то есть измерение напряжений и происходит автоматически.
Окончательная схема экспериментальной установки приведена на рисунке 26. Высокотемпературная ячейка с тиристорным регулятором переменного тока позволяет нагревать исследуемый образец (в данном случае – пластинка монокристалла кремния) до различных температур, что обеспечивает различную проводимость, и, соответственно, различные годографы импеданса. Измерения производятся прибором ”ОСЦИГЕН”, вспомогательное устройство автоматизирует этот процесс и повышает точность измерения.
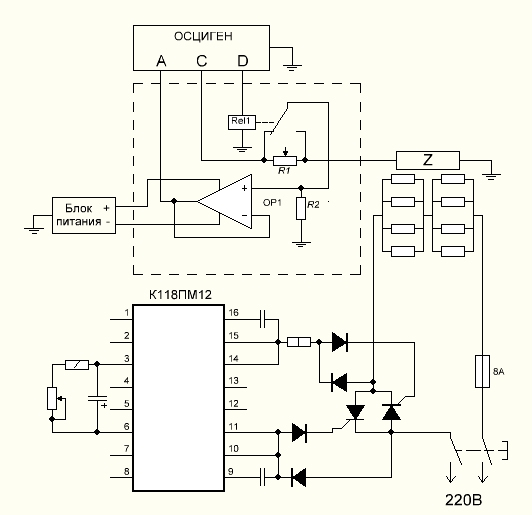
Рисунок 26 – Окончательная схема экспериментальной установки.
Данная установка пригодна только для грубой оценки параметров исследуемого материала. Для получения более точных результатов необходимо исключить влияние емкости кабелей, идущих от высокотемпературной ячейки к вспомогательному устройству, также необходимо, чтобы площадь образца как можно точнее соответствовала площади электродов высокотемпературной ячейки. Также, если суметь изготовить электроды высокотемпературной ячейки прозрачными, можно проводить эксперименты по взаимодействию исследуемого материала с излучением, что расширит список характеристик, получаемых из спектра импеданса.
Ниже представлен годограф импеданса для пробной паралелльной RC-цепочки, полученный с помощью вышеописанной установки. Емкость конденсатора , сопротивление резистора Точки – измерение импеданса по вышеописанной методике. Линия – теоретический расчет по формуле: (1/Z)=(1/R1) + i·(2·f·C1). Измерение и расчет делались для частот f в интервале от 10 килогерц до 3,6 мегагерц. По осям отложены действительная и мнимая части Z в омах.
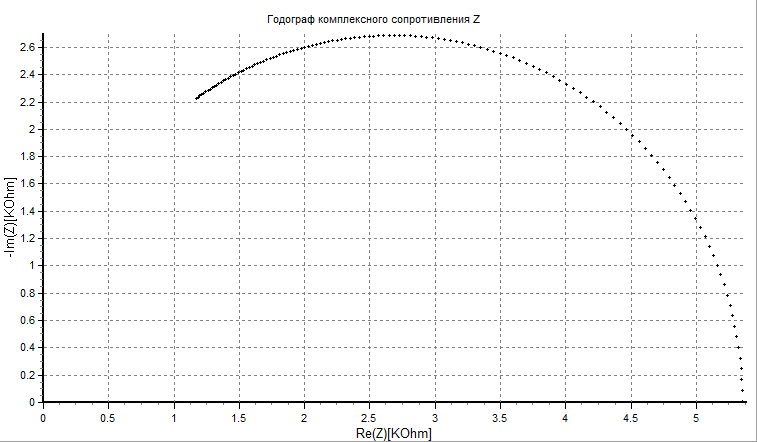
Рисунок 27 – Годограф импеданса паралелльной RC-цепочки.
4 Расчет характеристик и анализ полученных результатов
4.1 Расчет эквивалентных схем замещения
Измерения производились при четырех значениях температуры, ниже приведены годографы импеданса для каждого измерения.
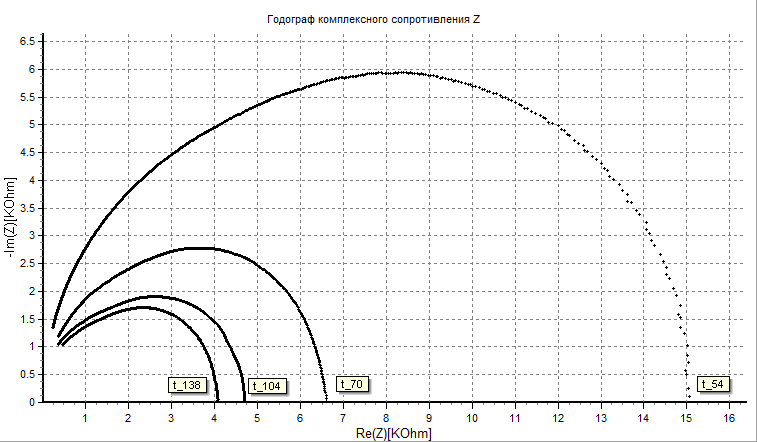
Рисунок 28 – Годографы импеданса пластинки кремния при различных температурах.
Основы методики расчета эквивалентных схем описаны в пункте 2.1. При измерении импеданса прибор “ОСЦИГЕН” формирует текстовый файл со значениями частоты, реальной и мнимой частями импеданса. Из файла выбираются значение частоты, соответствующее максимальной мнимой части импеданса, и максимальная реальная часть импеданса. Максимальная реальная часть импеданса соответствует активному сопротивлению, то есть значению R в эквивалентной схеме замещения, а значение емкости вычисляется из соотношения, указанного на рисунке 19:
(74)
где – частота, соответствующая максимальному значению мнимой части импеданса.
Приведем значения и для каждой температуры (начиная с самой низкой): , , , , , , , . Тогда можно рассчитать значения С для каждой температуры по формуле (74):
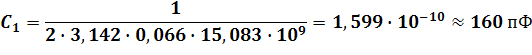
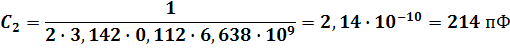
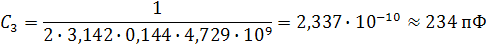
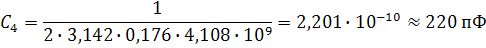
Таким образом, исследуемый образец можно представить, например, при температуре , как паралелльную RC-цепочку с сопротивлением и емкостью . С помощью рассчитаных значений можно рассчитать некоторые характеристики материала, напрмер диэлектрическую проницаемость.
4.2 Расчет диэлектрической проницаемости
Рассчитать диэлектрическую проницаемость исследуемой кремниевой пластинки можно также с помощью выражения 74.
Запишем в выражении 74 как формулу плоского конденсатора:

и выразим отсюда :
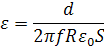
Площадь обкладок конденсатора можно принять равной площади поверхности кремниевой пластинки. Но как уже писалось выше, для более точного измерения необходимо, чтобы площади электродов высокотемпературной ячейки и площадь исследуемого образца совпадали как можно точнее. За расстояние между обкладками примем толщину исследуемого образца. В данном случаем, так как образец представляет собой круглую пластинку радиусом и толщиной , можно записать:
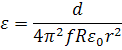
Теперь рассичаем значение для каждой температуры, начиная с самой низкой:
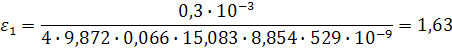
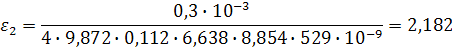
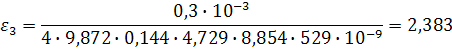
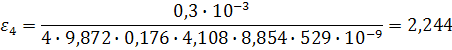
Можно заметить, что полученные значения очень сильно отличаются от табличного значения для кремния – 11,7. Это связано с тем, что значение диэлектрическо проницаемости сильно зависит от частоты электрического поля.
С увеличением частоты в области низких частот полярных диэлектриков остается постоянной до тех пор, пока время релаксации дипольных молекул остается меньше полупериода электрического поля (), т. е. за это время диполи успевают полностью упорядочиться в направлении поля. При дальнейшем росте частоты, когда время полупериода становится меньше времени релаксации, которое от частоты не зависит, начинает уменьшаться вплоть до значений, определяемых электронной поляризацией. Следовательно, на высоких частотах дипольная поляризация отсутствует (), так как диполи не успевают следовать за электрическим полем. Область уменьшения в ее частотной зависимости называется дисперсией диэлектрической проницаемости.
4.3 Анализ полученных результатов.
На основе экспериментальных данных и проведенных расчетов были получены зависимости сопротивления от частоты и зависимость емкости от сопротивления и частоты. Можно заметить, что зависимость для емкости является немонотонной на участке функцией. Также были построены годографы для каждой температуры на основе экспериментальных данных и для RC-цепочки с такими же параметрами. Можно заметить некоторое несовпадение теоретических данных с экспериментом. Это может быть связано как с некоторыми эффектами, возникающими в исследуемом образце (например, поверхностная емкость), так и с несовершенством лабораторной экспериментальной установки (об этом упоминалось выше). Ниже приведены все перечисленные графики.
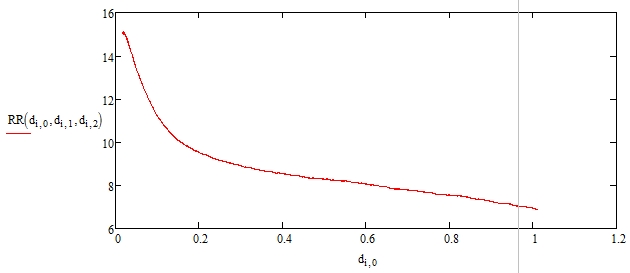
Рисунок 29 – Зависимость сопротивления от частоты.
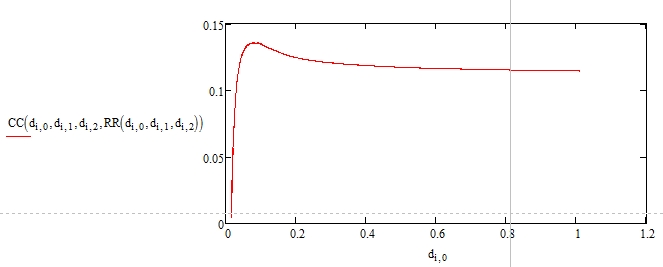
Рисунок 30 – Зависимость емкости от сопротивления и частоты.
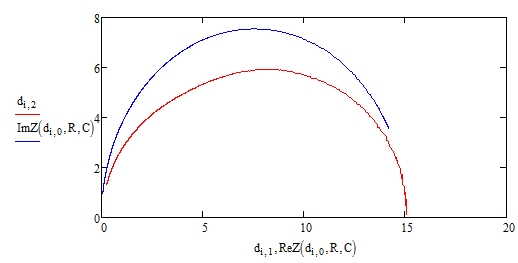
Рисунок 31 – Идеальный и реальный годографы при .
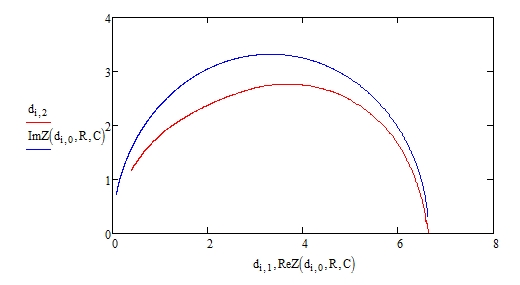
Рисунок 32 – Идеальный и реальный годографы при .
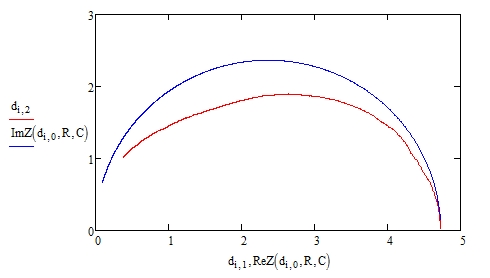
Рисунок 33 – Идеальный и реальный годографы при .
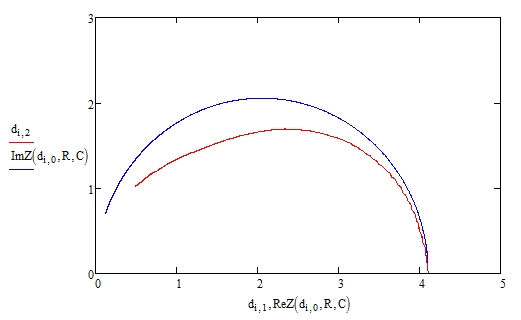
Рисунок 34 – Идеальный и реальный годографы при .
ЗАКЛЮЧЕНИЕ
В ходе данной работы был проведен теоретический литературный обзор по теме импедансной спектроскопии, методов его измерения и описания. Было сконструировано оборудование, необходимое для проведения эксперимента по импедансной спектроскопии, а именно – высокотемпературная ячейка и вспомогательное устройство для прибора ”ОСЦИГЕН”.
Используя сконструированное оборудование, прибор ”ОСЦИГЕН” и его виртуальную среду была проведена серия экспериментов по измерению импеданса с нагреванием пластинки кремния. На основе полученных годографов импеданса были рассчитаны эквивалентные схемы замещения.
Из спектров импеданса была получена такая характеристика материала, как диэлектрическая проницаемость среды. При дальнейшем развитии и совершенствовании метода можно будет получать ряд других характеристик материала.
Были предложены методы по совершенствованию и оптимизации экспериментального оборудования для получения различных характеристик исследуемого материала.
В ходе выполнения данной выпускной квалификационной работы были получены навыки проведения научных исследований в избранной области экспериментальных физических исследований с помощью современной приборной базы, а именно с помощью прибора ”ОСЦИГЕН” и сконструированного оборудования, и с помощью таких информационных технологий, как система компьютерной алгебры Mathcad (ПК-2).
Также в ходе выполнения были приобретены и освоены навыки применения на практике профессиональных знаний теории и методов физических исследований, отраженных в расчете эквивалентных схем замещения и диэлектрической проницаемости среды (ПК-3).
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Поклонский Н. А. Основы импедансной спектроскопии композитов / Н. А. Поклонский, Н. И. Горбачук. –Минск, БГУ, 2005. – 131с.
2 Тонконогов М. П. Диэлектрическая спектроскопия кристаллов с водородными связями. Протонная релаксация / М. П. Тонконогов // Успехи физических наук. – 1998. – Т.168. – № 1. – С. 29-54.
3 Васильев Р. Б. Метод спектроскопии импеданса для исследования электрофизических свойств материалов: [Методическая разработка к программам повышения квалификации] / Р. Б. Васильев – Москва, 2011. – 49 с.
4 Челидзе Т. Л. Электрическая спектроскопия гетерогенных систем / Т. Л. Челидзе, А. И. Деревянко, О. Д. Куриленко. – Киев: Наукова думка, 1977. – 231 с.
5 Забродский А. Г. Электронные свойства неупорядоченных систем / А. Г. Забродский, С. А. Немов, Ю. И. Равич. – СПб.: Наука, 2000. – 72 c.
6 Виноградов А. П. Электродинамика композиционных материалов / А. П. Виноградов; под ред. Б. З. Каценеленбаума. – М.: Эдиториал УРСС, 2001. – 208 с.
7 Графов Б. М. Электрохимические цепи переменного тока / Б. М. Графов, Е. А. Укше. – М.: Наука, 1973. – 128 с.
8 Гуль В. Е. Электропроводящие полимерные композиты / В. Е. Гуль, Л. З. Шенфиль. – М.: Химия, 1984. – 248 с.
9 Шкловский Б. И. Электронные свойства легированных полупроводников / Б. И. Шкловский, А. Л. Эфрос. – М.: Наука, 1979. – 416c.
10 Касаткин А. С. Электротехника / А. С. Касаткин, М. В. Немцов. –
М.: Издательский центр “Академия”, 2003. – 544 с.
11 Ред Э. Справочное пособие по высокочастотной схемотехнике: Схемы, блоки, 50-омная схемотехника / Э. Ред. – М.: Мир, 1990. – 256 с.
12 Хоровиц П. Искусство схемотехники / П. Хоровиц, У. Хилл. – М.: Бином, 2014. – 700 с.
13 Пат. 33237 Российская Федерация. Многофункциональный цифровой вычислительный прибор для измерения и генерации сигналов ”ОСЦИГЕН” / Заборовский В.С., Игнатьев Б.В., Гук М.Ю. – Приоритет 20.06.2003.
14 Игнатьев Б.В. / Универсальный регистратор сигнала фотоэлектронного умножителя. // Материалы ХVIII Всероссийской конференции «Оптика и спектроскопия конденсированных сред», 16–22 сентября 2012 г. – Краснодар. – С. 190–191.
15 Игнатьев Б.В. / Использование прибора «ОСЦИГЕН» для радиоспектроскопии. // Материалы ХIX Всероссийской конференции «Оптика и спектроскопия конденсированных сред», 29 сентября – 5 октября 2013 г. – Краснодар. – С. 170–171.
ВЫСОКОТЕМПЕРАТУРНАЯ ЯЧЕЙКА ДЛЯ ИМПЕДАНСНОЙ СПЕКТРОСКОПИИ КРИСТАЛЛОВ