Трехмерные геометрические преобразования
Лекция 4
Трехмерные геометрические преобразования
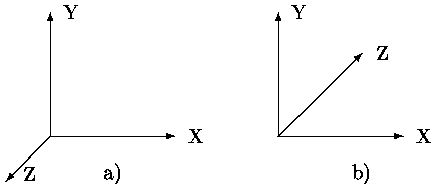
Далее при рассмотрении трехмерных преобразований, в основном, используется общепринятая в векторной алгебре правая система координат (рис. а). При этом, если смотреть со стороны положительной полуоси в центр координат, то поворот на +90° (против часовой стрелки) переводит одну положительную ось в другую (направление движения расположенного вдоль оси и поворачивающегося против часовой стрелки правого винта и положительной полуоси совпадают). В некоторых, специально оговариваемых случаях, используется левая система координат (см. рис. б). В левой системе координат положительными будут повороты по часовой стрелке, если смотреть с положительного конца полуоси. В трехмерной машинной графике более удобной является левая система координат. Тогда если, например, поверхность экрана совмещена с плоскостью XY, то большим удалениям от наблюдателя соответствуют точки с большим значением Z (см. рис. б).
Работа с однородными трехмерными координатами и матрицами преобразования (формирование и композиция) подобна таковой для двумерного случая, поэтому здесь будут рассмотрены только матрицы преобразований сдвига, масштабирования и поворота и пример конструирования матрицы преобразования по известному его результату.
Подобно тому как в двумерном случае точка в однородных координатах представляется трехмерным вектором [ X Y W ], а матрицы преобразований имеют размер 33, для трехмерного случая точка представляется четырехмерным вектором [ X Y Z W ], где W не равно 0, а матрицы преобразований имеют размер 44.
Формулы для преобразования:
Если W не равно 1, то декартовые координаты точки (x,y,z) получаются из соотношения:
|
[ x y z 1 ] = [ (X/W) (Y/W) (Z/W) 1 ].
|
Параллельный перенос:
Р` = РТ;
1 0 0 0
0 1 0 0 - матрица переноса
0 0 1 0
Tx Ty Tz 1
Масштабирование:
Р` = РS;
Sx 0 0 0
0 Sy 0 0 , S – матрица
0 0 Sz 0
0 0 0 1
Поворот:
При повороте в 3-х мерном пространстве существует 3 поворота вокруг каждой из осей.
Кроме того, существует 2 системы координат: правая и левая.
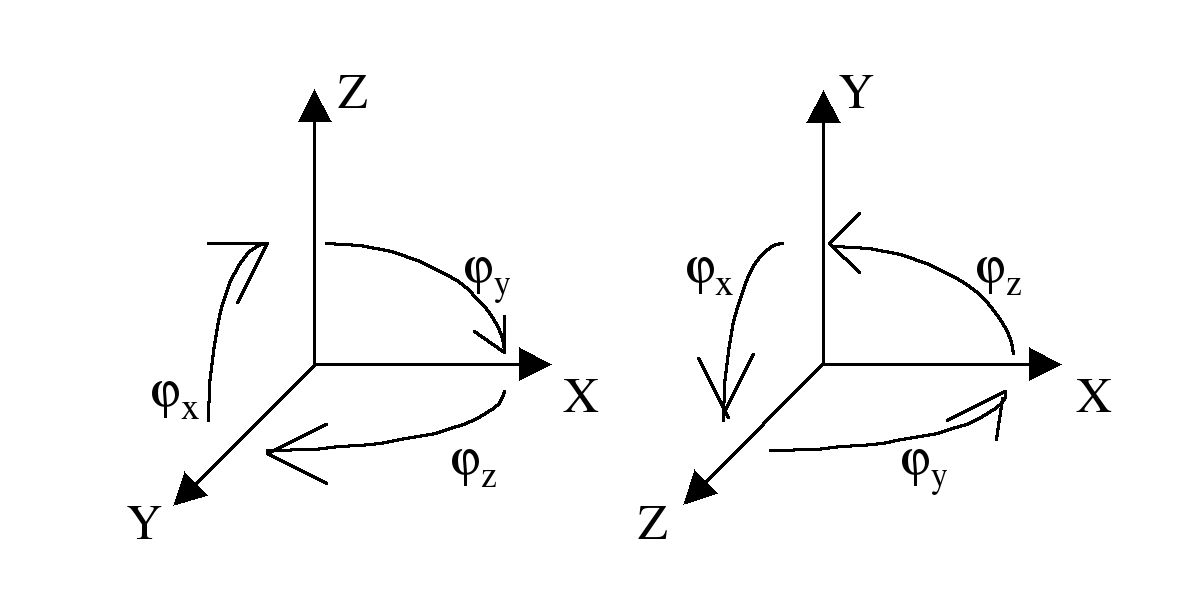
Ранее рассмотренная для двумерного случая матрица поворота является в то же время трехмерным поворотом вокруг оси Z. Так как при трехмерном повороте вокруг оси Z (поворот в плоскости XY) размеры вдоль оси Z неизменны, то все элементы третьей строки и третьего столбца равны 0, кроме диагонального, равного 1:
|
Rz(fz) =
|
|
|
cosfz
|
sinfz
|
0
|
0
|
|
|
.
|
|
|
|
|
-sinfz
|
cosfz
|
0
|
0
|
|
|
|
|
|
|
|
0
|
0
|
1
|
0
|
|
|
|
|
|
|
|
0
|
0
|
0
|
1
|
|
|
|
При повороте вокруг оси X (в плоскости YZ) размеры вдоль оси X не меняются, поэтому все элементы первой строки и первого столбца равны 0, за исключением диагонального, равного 1:
|
Rx(fx) =
|
|
|
1
|
0
|
0
|
0
|
|
|
.
|
|
|
|
|
0
|
cosfx
|
sinfx
|
0
|
|
|
|
|
|
|
|
0
|
-sinfx
|
cosfx
|
0
|
|
|
|
|
|
|
|
0
|
0
|
0
|
1
|
|
|
|
При повороте вокруг оси Y (в плоскости XZ) размеры вдоль оси Y не меняются, поэтому все элементы второй строки и второго столбца равны 0, за исключением диагонального, равного 1:
|
Ry(fy) =
|
|
|
cosfy
|
0
|
-sinfy
|
0
|
|
|
.
|
|
|
|
|
0
|
1
|
0
|
0
|
|
|
|
|
|
|
|
sinfy
|
0
|
cosfy
|
0
|
|
|
|
|
|
|
|
0
|
0
|
0
|
1
|
|
|
|
В общем случае любой поворот в пространстве может быть описан с помощью некоторых комбинаций этих трех поворотов. Причём повороты не обладают свойством коммутативности:
RX RY RZ RZ RX RY.
Любой произвольный поворот может быть представлен 6 сочетаниями элементарных поворотов. Причем в каждом случае будут свои углы (за исключением вырожденных ситуаций).
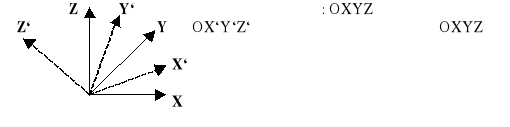
P` = P R, где R – матрица поворотов.
P` = [X`, Y`, Z`, 1];
P = [X, Y, Z, 1];
Элементы R – косинусы соответствующих углов.
a1 a2 a3 0 cos(XOX`) cos(XOY`) cos(XOZ`) 0
b1 b2 b3 0 cos(YOX’) cos(YOY’) cos(YOZ’) 0
c1 c2 c3 0 cos(ZOX’) cos(ZOY’) cos(ZOZ’) 0
0 0 0 1 0 0 0 1
Элементы матрицы R можно также рассматривать в виде векторов:
`i, `j, `k – это вектора единичной длины.
`N1 = `i ·a1 +`j ·b1 +`k·c1 `M1 = `i ·a1 +`j ·a2 +`k·a3
`N2 = `i ·a2 +`j ·b2 +`k·c2 `M2 = `i ·b1 +`j ·b2 +`k·b3
`N3 = `i ·a3 +`j ·b3 +`k·c3 `M3 = `i ·c1 +`j ·c2 +`k·c3
Запишем векторное произведение:
`N1 `N2 =`N3 `M1 `M2 =`M3
`N2 `N3 =`N1 `M2 `M3 =`M1
`N3 `N1 =`N2 `M3 `M1 =`M2
Скалярное произведение:
`N1 ·`N2 =`N1 ·`N3 =`N2 ·`N3 = 0
Композиция 3D изображений
P` = P·M; P = P`· М–1
Поворот вокруг произвольной оси, проходящей через начало координат:
z
(l, m, n)
l2+cos(j)·(1–l2) l·(1–cos(j))·m+n·sin(j) l·(1–cos(j))·n–m·sin(j) 0
l·(1–cos(j))·m m2+cos(j)·(1–m2) m·(1–cos(j))·n+l·sin(j) 0
l·(1–cos(j))·n+m·sin(j) m·(1–cos(j))·n–l·sin(j) n2+cos(j)·(1–n2) 0
0 0 0 1
M – в общем случае не ортогональная матрица, т.е. М–1 МТ,
а R–ортогональная (R–1=RT).
В общем виде матрица преобразований имеет вид:
m11 m12 m13 0
m21 m22 m23 0
M = m31 m32 m33 0
m41 m42 m43 1
Координаты точки вычисляются по следующим формулам:
X` = X*m11+Y* m21+ Z* m31+ m41
Y` = X*m12+Y* m22+ Z* m32+ m42
Z` = X*m13+Y* m23+ Z* m33+ m43
Движение по рельефу
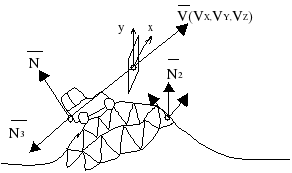
Нормаль к поверхности определяет N2 => a2b2c2
Vz как правило не известен