СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ

Лекция 6

Тема. СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ

Цель. Дать понятие распознавания цифрового сигнала.

Учебная. Разъяснить процесс распознавания цифрового сигнала.

Развивающая. Развивать логическое мышление и естественное - научное мировоззрение.

Воспитательная. Воспитывать интерес к научным достижениям и открытиям в отрасли телекоммуникации.

Межпредметные связи:

Обеспечивающие: информатика, математика, вычислительная техника и МП, системы программирования.

Обеспечиваемые: Стажерская практика

Методическое обеспечение и оборудование:

Методическая разработка к занятию.

Учебный план.

Учебная программа

Рабочая программа.

Инструктаж по технике безопасности.

Технические средства обучения: персональный компьютер.

Обеспечение рабочих мест:

Рабочие тетради

Ход лекции.

Организационный момент.

Анализ и проверка домашней работы

Ответьте на вопросы:

  1. В чем заключается отличие цифровых сигналов от аналоговых?
  2. Какие классы диаграмм используются при проведении измерений?
  3. Дайте краткое описание каждому классу.
  4. Что используется для построения глазковой диаграммы?
  5. Поясните суть глазковой диаграммы.

План лекции

  1. МЕТОД БАЙЕСА
  • Основы метода
  • Обобщенная формула Байеса.
  • Диагностическая матрица.
  • Решающее правило
    1. МЕТОД ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА
  • Основы метода.
  • Общая процедура метода.
  • Связь границ принятия решения с вероятностями ошибок первого и второго рода.

Основное преимущество статистических методов распознавания состоит в возможности одновременного учета признаков различной физической природы, так как они характеризуются безразмерными величинами — вероятностями их появления при различных состояниях системы.

  1. МЕТОД БАЙЕСА

Среди методов технической диагностики метод, основанный на обобщенной формуле Байеса (Теорема Байеса (или формула Байеса) — одна из основных теорем теории вероятностей, которая позволяет определить вероятность того, что произошло какое-либо событие(гипотеза) при наличии лишь косвенных тому подтверждений (данных), которые могут быть неточны), занимает особое место благодаря простоте и эффективности.

Метод Байеса имеет недостатки: большой объем предварительной информации, «угнетение» редко встречающихся диагнозов и др. Однако в случаях, когда объем статистических данных позволяет применить метод Байеса, его целесообразно использовать как один из наиболее надежных и эффективных методов.

Основы метода. Метод основан на простой формуле Байеса. Если имеется диагноз Di и простой признак ki, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния Di и признака ki).

 Априорная вероятность — распределение вероятностей, которое выражает предположения до учёта экспериментальных данных.

Априорное распределение вероятностей (англ. prior probability distribution, или просто prior) неопределённой величины p — распределение вероятностей, которое выражает предположения о p до учёта экспериментальных данных.

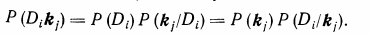(3.1)

Из этого равенства вытекает формула Байеса

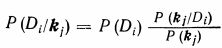(3.2)

Очень важно определить точный смысл всех входящих в эту формулу величин.

P(Di)- априорная вероятность гипотезы D

P(ki/Di) - вероятность гипотезы ki при наступлении события D (апостериорная вероятность - вероятность случайного события при условии того, что известны апостериорные данные, т.е. полученные после опыта.)

P(ki) - полная вероятность наступления события  ki

P(Di/ki) - вероятность наступления события Di при истинности гипотезы ki

Р(D)— вероятность диагноза D, определяемая по статистическим данным (априорная вероятность диагноза). Так, если предварительно обследовано N объектов и у W,- объектов имелось состояние D, то

P(Di) = Ni/N. (3.3)

Р (kj/Di) — вероятность появления признака kj; у объектов с состоянием Di. Если среди Ni, объектов, имеющих диагноз Di, у Nij проявился признак kj то

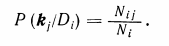(3.4)

Р (kj) — вероятность появления признака kj во всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N объектов признак к} был обнаружен у Nj объектов, тогда

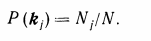(3.5)

В равенстве (3.2) Р (Di/kj) — вероятность диагноза D после того, как стало известно наличие у рассматриваемого объекта признака kj (апостериорная вероятность диагноза).

Обобщенная формула Байеса.

Эта формула относится к случаю, когда обследование проводится по комплексу признаков K, включающему признаки k1,k2 ..., kv. Каждый из признаков kj имеет тj разрядов (kj1 kj2 ..., kjS ..., kjm). В результате обследования становится известной реализация признака kj* = kjs (3.6) и всего комплекса признаков K*. Индекс *, как и раньше, означает конкретное значение (реализацию) признака. Формула Байеса для комплекса признаков имеет вид

Р (Di/K*) = Р (Di) Р (K*/Di)/P (K*) (i = 1, 2, ...,n), (3.7)

где Р (Di/K*) — вероятность диагноза D после того, как стали известны результаты обследования по комплексу признаков K, Р (Di) — предварительная вероятность диагноза D (по предшествующей статистике).

Формула (3.7) относится к любому из п возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний и потому

(3.8)

В практических задачах нередко допускается возможность существования нескольких состояний А1 ... An, причем некоторые из них могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов Di следует рассматривать отдельные состояния Di= А1, ..., Dr = Аr и их комбинации

Dr+i = A1A2 ••• и т. п.

В большинстве практических задач, особенно при большом числе признаков, можно принимать условие независимости признаков даже при наличии существенных корреляционных связей между ними.

Вероятность появления комплекса признаков K*

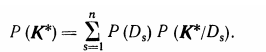. (3.11)

Обобщенная формула Байеса может быть записана так:

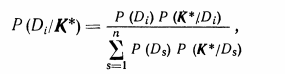(3.12)

где Р (K*/Di) определяется равенством. Из обобщенной формулы Байеса (3.12) вытекает что, разумеется,

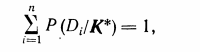(3.13)

и должно быть, так как один из диагнозов обязательно реализуется, а реализация одновременно двух диагнозов невозможна.

Следует обратить внимание на то, что знаменатель формулы Байеса для всех диагнозов одинаков. Это позволяет сначала определить вероятности совместного появления 1-го диагноза и данной реализации комплекса признаков и затем апостериорную вероятность диагноза

Отметим, что иногда целесообразно использовать предварительное логарифмирование формулы (3.12).

Если реализация некоторого комплекса признаков K* является детерминирующей (детерминирующая - определяющая направленность, избирательность в зависимости от поставленной задачи.) для диагноза Dp, то этот комплекс не встречается при других диагнозах:

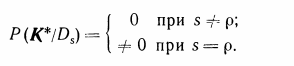
Тогда, в силу равенства (3.12)

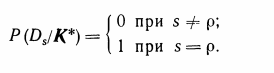
Таким образом, детерминистская логика установления диагноза является частным случаем вероятностной логики. Формула Байеса может использоваться и в том случае, когда часть признаков имеет дискретное распределение, а другая часть — непрерывное. Для непрерывного распределения используются плотности распределения. Однако в расчетном плане указанное различие признаков несущественно, если задание непрерывной кривой осуществляется с помощью совокупности дискретных значений.

Диагностическая матрица.

Для определения вероятности диагнозов по методу Байеса необходимо составить диагностическую матрицу (табл. 1), которая формируется на основе предварительного статистического материала. В этой таблице содержатся вероятности разрядов признаков при различных диагнозах. Если признаки двухразрядные (простые признаки «да—нет»), то в таблице достаточно указать вероятность появления признака P(kj,/Di).

Таблица 1

Диагностическая матрица в методе Байеса

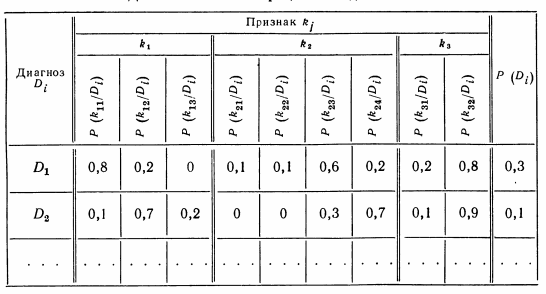
В диагностическую матрицу включены априорные вероятности диагнозов. Процесс обучения в методе. Байеса состоит в формировании диагностической матрицы. Важно предусмотреть возможность уточнения таблицы в процессе диагностики. Для этого в памяти ЭВМ следует хранить не только значения вероятности, но и следующие величины: N — общее число объектов, использованных для составления диагностической матрицы; Nt — число объектов с диагнозом D; Nij — число объектов с диагнозом D, обследованных по признаку Kj.

Решающее правило — правило, в соответствии с которым принимается решение о диагнозе. В методе Байеса объект с комплексом признаков К* относится к диагнозу с наибольшей (апостериорной) вероятностью (Апостериорная вероятность - условная вероятность случайного события при условии того, что известны данные, полученные после опыта)

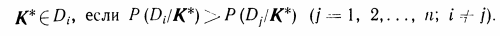(3.19)

Символ Є, применяемый в функциональном анализе, означает принадлежность множеству. Условие (3.19) указывает, что объект, обладающий данной реализацией комплекса признаков К* или, реализация K* принадлежит диагнозу (состоянию) D. Правило (3.19) обычно уточняется введением порогового значения для вероятности диагноза:

P(Di/K*)>Pi, (3.20)

где Pi — заранее выбранный уровень распознавания для диагноза D. При этом вероятность ближайшего конкурирующего диагноза не выше 1 — Pi . Обычно принимается Pi > 0,9. При условии

P(Di/K*)Pi, (3.21)

решение о диагнозе не принимается (отказ от распознавания) и требуется поступление дополнительной информации.

Процесс принятия решения в методе Байеса при расчете на ЭВМ происходит достаточно быстро.

Как указывалось, методу Байеса присущи некоторые недостатки, например погрешности при распознавании редких диагнозов. При практических расчетах целесообразно провести диагностику и для случая равновероятностных диагнозов, положив

P(D)i=1/n. (3.22)

Тогда наибольшим значением апостериорной вероятности будет обладать диагноз D, для которого P(D)i максимальна:

Иными словами, устанавливается диагноз D, если данная совокупность признаков чаще встречается при диагнозе D, чем при других диагнозах. Такое решающее правило соответствует методу максимального правдоподобия. Из предыдущего вытекает, что этот метод является частным случаем метода Байеса при одинаковых априорных вероятностях диагнозов. В методе максимального правдоподобия «частые» и «редкие» диагнозы равноправны.

  1. МЕТОД ПОСЛЕДОВАТЕЛЬНОГО АНАЛИЗА

Метод последовательного анализа, предложенный Вальдом, применяется для дифференциальной диагностики (распознавания двух состояний). В отличие от метода Байеса, число обследований заранее не устанавливается, их проводится столько, сколько необходимо для принятия решения с определенной степенью риска.

Основы метода. При использовании метода Байеса для распознавания состояний D1 и D2 следует составить отношение (для независимых признаков)

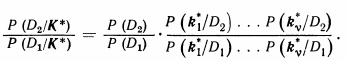
Если

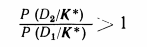
или

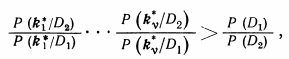
то принимается решение К*Є D2

В методе последовательного анализа рассматриваемые отношения вероятностей признаков (отношения правдоподобия) составляются не сразу, а в последовательном порядке; поэтому, как правило, требуется меньшее число обследований. Подобная форма применяется при нормальном распределении количественных признаков.

Общая процедура метода. Будем для краткости считать, что признаки являются независимыми. Пусть проведено v — 1 обследований, которые еще не дали возможности принятия решения,

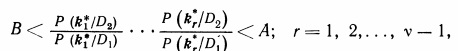
но после v-ro обследования

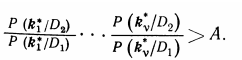
Тогда принимается решение об отнесении объекта к диагнозу D2 . К*Є D2. Если после v-гo обследования

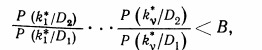
то объект относится к диагнозу D1.

Для сокращения объема обследований следует вначале проводить обследование по наиболее информативным признакам.

Связь границ принятия решения с вероятностями ошибок первого и второго рода.

При распознавании могут быть ошибки двоякого рода.

Ошибка относящаяся к диагнозу D1 (принимается решение о наличии диагноза D2, когда в действительности объект принадлежит диагнозу D1), называется ошибкой первого рода. Ошибка, относящаяся к диагнозу D2 (принимается решение в пользу диагноза D1 когда справедлив диагноз D2), называется ошибкой второго рода.

Считая состояние D1 исправным, а состояние D2 дефектным, легко понять, что ошибка первого рода является «ложной тревогой», а ошибка второго рода «пропуском дефекта».

Обозначим вероятность ошибки первого рода , второго рода . Допустим, что имеются условия и принимается решение в пользу диагноза D2. Вероятность того, что это решение будет справедливым, равна 1— . Вероятность принадлежности объекта с данной реализацией признаков к диагнозу D1 составляет . С другой стороны, в силу соотношения вероятность диагноза D2, по крайней мере, в А раз больше, чем диагноза D1 т. е.

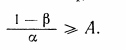(4.11)

Подобным образом можно получить и следующую оценку:

(4.12)

В практических расчетах часто принимают = = 0,05 или = = 0,10.

Домашнее задание: § конспект.

Закрепление материала:

Ответьте на вопросы:

  1. Что позволяет определить формула Байеса?
  2. В чем состоят основы метода Байеса? Приведите формулу. Дайте определение точного смысла всех входящих в эту формулу величин.
  3. Что означает, что реализация некоторого комплекса признаков K* является детерминирующей?
  4. Объясните принцип формирования диагностической матрицы.
  5. Что означает решающее правило принятия?
  6. Дайте определение методу последовательного анализа.
  7. В чем состоит связь границ принятия решения с вероятностями ошибок первого и второго рода?

Литература:

Амренов С. А. «Методы контроля и диагностики систем и сетей связи» КОНСПЕКТ ЛЕКЦИЙ -: Астана, Казахский государственный агротехнический университет, 2005 г.

И.Г. Бакланов Тестирование и диагностика систем связи. - М.: Эко-Трендз, 2001.

Биргер И. А. Техническая диагностика.— М.: «Машиностроение», 1978.—240,с, ил.

АРИПОВ М.Н , ДЖУРАЕВ Р.Х., ДЖАББАРОВ Ш.Ю. «ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ЦИФРОВЫХ СИСТЕМ» -Ташкент, ТЭИС, 2005

Платонов Ю. М., Уткин Ю. Г. Диагностика, ремонт и профилактика персональных компьютеров. -М.: Горячая линия - Телеком, 2003.-312 с: ил.

М.Е.Бушуева, В.В.Беляков Диагностика сложных технических систем Труды 1-го совещания по проекту НАТО SfP-973799 Semiconductors. Нижний Новгород, 2001

Малышенко Ю.В. ТЕХНИЧЕСКАЯ ДИАГНОСТИКА часть I конспект лекций

Платонов Ю. М., Уткин Ю. Г.Диагностика зависания и неисправностей компьютера/Серия «Техномир». Ростов-на-Дону: «Феникс», 2001. — 320 с.

PAGE \* MERGEFORMAT 5

СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ