Сравнительный анализ эконометрических моделей регрессии

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Тверской государственный технический университет»

(ТвГТУ)

Институт дополнительного профессионального образования

Кафедра «Бухгалтерский учет, анализ и аудит»

Курсовой проект

По дисциплине: «Эконометрика»

На тему: «Сравнительный анализ эконометрических моделей регрессии»

ВЫПОЛНИЛА: студентка 3курса

Института ДПО и П

Группы РБАиА-37-12

Замятина

Кристина Дмитриевна

(Ф.И.О. студента)

ПРОВЕРИЛА:

Коновалова А. С.

(Ф.И.О. преподавателя)

Ржев 2015

Содержание

ВВЕДЕНИЕ

ГЛАВА 1. АНАЛИТИЧЕСКАЯ ЧАСТЬ

Основы эконометрического исследования моделей регрессии.

Технология эконометрического исследования моделей регрессии.

ГЛАВА 2. ПРОЕКТНАЯ ЧАСТЬ

2.1 Информационно-методическое обеспечение

эконометрического исследования

2.2. Пример эконометрического исследования.

Парная и множественная регрессии.

ЗАКЛЮЧЕНИЕ

Список ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

ВВЕДЕНИЕ

Эконометрика – это наука, предметом изучения которой являются количественные закономерности и взаимозависимости в экономике на основании методов математической статистики. Основой эконометрики является построение эконометрической модели и определение возможностей использования данной модели для описания, анализа и прогнозирования реальных экономических процессов.

Создавая возможность для принятия обоснованных экономических решений, эконометрический анализ является основой экономического анализа и прогнозирования.

В любой области экономики деятельность специалиста требует применения современных методов работы, основанных на эконометрических моделях, концепциях и приемах.

В качестве предмета эконометрического исследования в курсовом проекте выбрано количество прибывших в страны ЕС на постоянное место жительства. Миграционные процессы являются чрезвычайно важным фактором для оценки перспектив развития общества, поэтому актуальность темы исследования обуславливает рост социальной значимости этих процессов в современном мире.

Экономическое исследование миграционных процессов - существенный фактор повышения эффективности развития стран. История развития человечества неразрывно связана с изменениями динамики численности населения. В Европе быстрый рост населения обусловлен в первую очередь социально-экономическими изменениями, т.е. следует за экономическим ростом и изменениями в социальной сфере.

Цели курсового проекта – разработка проектных решений по информационно-методическому обеспечению исследования в области эконометрического моделирования, а также получение практических навыков построения и исследования эконометрических моделей.

Задача курсового проекта – использование на практике знаний и навыков в построении и исследовании эконометрических моделей для проведения эконометрического анализа данных.

Конечной прикладной целью эконометрического моделирования реальных социально-экономических процессов в данном курсовом проекте является прогноз экономических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы, то есть определение тенденций миграционных процессов в странах ЕС и их зависимость от имеющихся факторов, учитываемых при построении эконометрической модели.

ГЛАВА 1. АНАЛИТИЧЕСКАЯ ЧАСТЬ

1.1. Основы эконометрического исследования моделей регрессии.

Экономической дисциплиной, занимающейся разработкой и применением статистических методов для измерения взаимосвязей между эконометрическими переменными, является эконометрика, представляющая собой комбинацию экономической теории, статистики и математики.

Эконометрические данные не являются результатами контролируемого эксперимента. Эконометрика имеет дело с конкретными экономическими данными и занимается количественным описанием конкретных взаимосвязей, то есть заменяет коэффициенты, представленные в общем виде, конкретными численными значениями. В эконометрике разрабатываются специальные методы анализа, позволяющие снизить влияние ошибок измерения на полученные результаты.

Главный инструмент эконометрики - эконометрическая модель, то есть формализованное описание количественных взаимосвязей между переменными. В методологии моделирования заложены большие возможности саморазвития, поскольку моделирование – это циклический процесс, за каждым циклом может последовать следующий, а знания об исследуемом объекте расширяются и уточняются, исходная модель постепенно совершенствуется. Недостатки, обнаруженные после предыдущего цикла моделирования, обусловленные малым знанием объекта и ошибками в построении модели, можно исправить в последующих циклах.

Можно выделить три класса эконометрических моделей:

- модель временных данных;

- регрессионная модель с одним уравнением;

- система одновременных уравнений.

Классификация задач, решаемых с помощью эконометрической модели: 1) по конечным прикладным целям:

- прогноз эконометрических и социально-экономических показателей, характеризующих состояние и развитие анализируемой системы;

- имитация возможных сценариев социально-экономического развития системы.

2) по уровню иерархии:

- задачи макроуровня (страна в целом);

- задачи мезоуровня (регионы, отрасли, корпорации);

- микроуровень (семья, предприятие, фирма).

3) по профилю эконометрической системы, направленные на изучение:

- рынка;

- инвестиционной, финансовой или социальной политики;

- ценообразование;

- распределительных отношений;

- спроса и потребления;

- комплекса проблем. [5]

Основные этапы эконометрического моделирования:

1 этап - постановочный. Определение конечных целей модели, набора участвующих в ней факторов и показателей, их роли. Основные цели исследований: анализ состояния и поведения экономического объекта, прогноз его экономических показателей, имитация развития объекта, выработка управленческих решений.

2 этап - априорный. Анализ сущности изучаемого объекта, формирование и формализация известной до начала моделирования информации.

3 этап - параметризация. Выбор общего вида модели, состава и формы входящих в нее связей. Основная задача этого этапа - выбор функции f(Х).

4 этап - информационный. Сбор необходимой статистической информации.

5 этап - идентификация модели. Статистический анализ модели и оценка ее параметров. Основная часть эконометрических исследований.

6 этап - верификация модели. Проверка адекватности модели, оценка точности модельных данных. Выясняется, насколько удачно решены проблемы спецификации и идентификации, какова точность расчетов по данной модели. Проверяется, насколько соответствует построенная модель моделируемому реальному экономическому объекту или процессу. [1]

При моделировании экономических процессов в эконометрических моделях используют:

1. Пространственные данные - набор сведений по разным объектам, взятым за один и тот же период времени.

2. Временные данные - набор сведений, характеризующих один и тот же объект, но за разные периоды времени.

Набор сведений представляет собой множество признаков, характеризующих объект исследования. Признаки могут выступать в одной из двух ролей: роль результативного признака и роль факторного признака.

Переменные делятся на:

- экзогенные, значения которых задаются извне;

- эндогенные, значения которых определяются внутри модели;

- лаговые - эндогенные или экзогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными;

- предопределенные - экзогенные переменные, привязанные к прошлым, текущим и будущим моментам времени и лаговые эндогенные переменные, уже известные к данному моменту времени.

В эконометрике в основном рассматривают ошибки спецификации модели, предполагая, что ошибки измерения сведены к минимуму. [2]

Спецификация модели - выбор вида функциональной зависимости (уравнения регрессии). Величина случайных ошибок не будет одна и та же для спецификаций модели, и сведение остаточного члена к минимуму позволяет выбрать наилучшую спецификацию.

Помимо выбора спецификации модели не менее важно также правильное описание структуры модели. Значение результативного признака может зависеть не от фактического значения объясняющей переменной, а от значения, которое ожидалось в предыдущем периоде.

Простейшая регрессионная модель всего лишь с двумя переменными входит в класс регрессионных моделей с одним уравнением, в которых одна объясняемая переменная представляется в виде функции от нескольких независимых (объясняющих) переменных и параметров. Этот класс включает модели множественной регрессии.

Более простыми являются модели временных рядов, которые объясняют поведение временного ряда, исходя только из его предыдущих значений, это модели:

- тренда,

- сезонности,

- авторегрессии,

- адаптивного прогноза,

- скользящего среднего и др. [4]

Более общими являются системы одновременных уравнений, в которых кроме объясняющих переменных в правых частях могут находиться также и объясняемые переменные из других уравнений, т.е. отличные от объясняемой переменной, стоящей в левой части данного уравнения.

При использовании отдельных уравнений регрессии предполагается, что факторы можно изменять независимо друг от друга, хотя в действительности их изменения не независимы, а изменение одной переменной чаще всего влечет за собой изменения во всей системе признаков, т.к. они являются взаимосвязанными. Необходимо уметь описывать структуру связей между переменными с помощью системы одновременных (структурных) уравнений.

Статистические и математические модели экономических явлений и процессов определяются спецификой той или иной области экономических исследований. Теория и практика экспертных оценок - важный раздел эконометрики, так как экспертные оценки используют для решения ряда экономических задач. [6]

Более известными в теоретических и учебных публикациях являются различные эконометрические модели, предназначенные для прогнозирования макроэкономических показателей. Это обычно модели, имеющие целью прогнозирование многомерного временного ряда. Они представляют собой систему линейных зависимостей между прошлыми и настоящими значениями переменных. В таких задачах оценивают как структуру модели, т.е. вид зависимости между значениями известных координат вектора в прежние моменты времени и их значениями в прогнозируемый момент, так и коэффициенты, входящие в эту зависимость. Структура такой модели - объект нечисловой природы. Свои эконометрические модели соответствуют каждой области экономических исследований. [8]

1.2. Технология эконометрического исследования моделей регрессии.

Исследование и количественная оценка объективно существующих взаимосвязей и зависимостей между экономическими явлениями - основная задача эконометрики.

Причинно-следственное отношение – это такая связь между явлениями, при которой изменение одного из них, называемого причиной, ведет к изменению другого, называемого следствием. Следовательно, причина всегда предшествует следствию.

Причинно-следственные отношения между явлениями представляют наибольший интерес для исследователя, что позволяет выявлять факторы, оказывающие основное влияние на вариацию изучаемых явлений и процессов.

Причинно-следственные связи в социально-экономических явлениях обладают следующими особенностями:

1. причина Х и следствие Y взаимодействуют не непосредственно, а через промежуточные факторы, которые при анализе опускаются.

2. социально-экономические явления развиваются и формируются в результате одновременного воздействия большого числа факторов. Одной из главных проблем при изучении этих явлений становится задача выявления основных причин и абстрагирование от второстепенных.

По направлению изменения связи подразделяются:

1. прямые (изменение результативного и факторного признаков происходит в одном направлении),

2. обратные (изменение результативного и факторного признаков происходит в противоположных направлениях).

По характеру проявления различают:

1. функциональная связь - связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака, проявляется во всех случаях наблюдения и для каждой конкретной единицы исследуемой совокупности, изучается в основном в естественных науках.

2. стохастическая зависимость - причинная зависимость, которая проявляется не в каждом отдельном случае, а в общем, при большом числе наблюдений, а одним и тем же значениям факторных признаков, как правило, соответствуют различные значения результативного признака, но, рассматривая всю совокупность наблюдений можно отметить наличие определенной зависимости между значениями признаков. Частным случаем стохастической связи является корреляционная связь, при которой изменение среднего значения результативного признака обусловлено изменением факторных признаков.

По аналитическому выражению выделяют связи:

1. линейные: изменение результативного признака прямо пропорционально изменению факторных признаков.

2. нелинейные.

Аналитически линейная стохастистическая связь между явлениями может быть представлена уравнением прямой линии на плоскости, либо уравнением гиперплоскости в n-мерном пространстве (при наличии n факторных переменных). [3]

Построение эконометрической модели - это основа эконометрического исследования. От того, насколько хорошо полученная модель описывает изучаемые закономерности между экономическими процессами, зависит степень достоверности результатов анализа и их применимости.

Построение эконометрической модели начинается со спецификации модели, заключающейся в получении ответа на два вопроса:

1) какие экономические показатели должны быть включены в модель;

2) какой вид имеет аналитическая зависимость между отобранными признаками.

В исследованиях, посвященных разработке методов прогнозирования таких финансовых показателей, как курсы валют, ценных бумаг, индексов широко применяются модели, основанные на предположении, что динамика этих процессов полностью определяется внутренними условиями.

После выделения совокупности рассматриваемых переменных следующим этапом является определение конкретного вида модели, наилучшим образом соответствующего изучаемому явлению.

По характеру связей факторов с переменной у модели подразделяются на линейные и нелинейные. По свойствам своих параметров модели подразделяются на модели с постоянной и переменной структурой.

Особый вид моделей составляют системы взаимосвязанных эконометрических уравнений.

Если на основе предварительного качественного анализа рассматриваемого явления не удается однозначно выбрать наиболее подходящий тип модели, то рассматриваются несколько альтернативных моделей, среди которых в процессе исследования выбирается та, которая в наибольшей степени соответствует изучаемому явлению. [7]

В общем случае процедуру построения эконометрической модели можно представить в виде следующих этапов:

1. Спецификация модели, т. е. выбор класса моделей, наиболее подходящих для описания изучаемых явлений и процессов.

Этот этап предполагает решение двух задач:

а) отбор существенных факторов для их последующего включения в модель;

б) выбор типа модели, т. е. выбор вида аналитической зависимости, связывающей включенные в модель переменные.

2. Оценка параметров модели, т. е. получение численных значений констант модели. При этом используется предварительно полученный массив исходных данных.

3. Проверка качества построенной модели и обоснование возможности ее дальнейшего использования. Наиболее сложным и трудоемким в эконометрическом исследовании является этап оценки параметров модели, где применяются методы теории вероятностей и математической статистики.

При решении проблемы выбора вида аналитической зависимости могут использоваться различные соображения:

- выводы аналитических исследований о качественном характере зависимости,

- описание свойств различных аналитических зависимостей,

- цели построения модели. [9]

Выбор вида эконометрической модели основывается, прежде всего, на результатах предварительного качественного или содержательного анализа, проводимого методами экономической теории. Характер предполагаемой зависимости обосновывается исходя из теоретически предположений о характере закономерности развития изучаемого явления или процесса.

Другой подход основан на анализе массива исходных данных, который позволяет выявить некоторые характеристики предполагаемых зависимостей и на этой основе сформулировать, как правило, несколько предположений о виде аналитической связи. Построенная модель используется для формулирования предположений о характере закономерности в развитии изучаемого явления, которые проверяются в течение дальнейших исследований.

Наибольшее применение в эконометрике нашли линейные модели.

Это обусловлено несколькими причинами:

- существуют эффективные методы построения таких моделей.

- в небольшом диапазоне значений факторных признаков линейные модели с достаточной точностью могут аппроксимировать реальные нелинейные зависимости.

- параметры модели имеют наглядную экономическую интерпретацию.

- прогнозы по линейным моделям, характеризуются меньшим риском значительной погрешности прогноза.

Важной составляющей процесса построения эконометрической модели является отбор факторов, существенно влияющих на изучаемый показатель и подлежащих включению в разрабатываемую модель. Оптимальный набор факторов определяется на основе качественного и количественного анализа.

На этапе постановки задачи и содержательного экономического анализа экономической модели отбираются факторы, влияние которых должно быть учтено при построении модели. В ряде случаев набор факторов определяется однозначно или с большой степенью уверенности. В более сложных случаях на следующем этапе с помощью формальных статистических методов проверяется целесообразность включения в модель каждого фактора. Прежде всего, факторы проверяются на наличие тесной линейной корреляционной зависимости между ними, существование которой приводит к получению ненадежных оценок параметров модели. [14]

Для преодоления сильной межфакторной корреляции применяются:

– исключение из модели одного или нескольких факторов. Из двух коррелирующих факторов исключаются тот, который более коррелирует с остальными факторами;

– преобразование факторов, при котором уменьшается корреляция между ними.

Одним из критериев включения факторов в модель является степень их изолированного влияния на результативный признак.

Два метода определения оптимального набора факторов:

1. метод включения. Строится уравнение регрессии с одним наиболее влияющим фактором, затем в него последовательно вводятся следующие факторы и определяется пара наиболее влияющих факторов, затем к первым двум добавляется еще по одному фактору и определяется наилучшая тройка факторов и т. д. На каждом шаге строится модель регрессии и проверяется значимость факторов. В модель включают только значимые факторы. Для проверки значимости фактора могут использоваться либо критерий Стьюдента, либо частный критерий Фишера. Процесс заканчивается, когда не остается факторов, которые следует включить в модель.

2. метод исключения. Строится уравнение регрессии с полным набором факторов, из числа которых затем последовательно исключаются незначимые или наименее значимые факторы. На каждом шаге исключается только один фактор, так как после исключения какого-либо фактора другой фактор, бывший до этого незначимым, может стать значимым. Процесс заканчивается, когда не остается факторов, которые следует исключить.

Методы включения и исключения не гарантируют определение оптимального набора факторов, но в большинстве случаев дают результаты либо оптимальные, либо близкие к ним. Не рекомендуется включать в модель очень большое число факторов, так как это может затруднить выявление качественных закономерностей и возрастает опасность включения в модель несущественных случайных факторов. Для получения надежных оценок параметров желательно, чтобы количество наблюдений превышало количество определяемых параметров не менее чем в 6-7 раз. [11]

После отбора факторов и выбора вида аналитической зависимости осуществляется оценка параметров модели. При оценке параметров модели в качестве исходных данных используется заранее подготовленный массив наблюдений. Качество оценок определяется наличием у них таких свойств как несмещенность, состоятельность и эффективность. Оценка параметра называется несмещенной, если ее математическое ожидание равно оцениваемому параметру. Оценка параметра называется состоятельной, если она сходится по вероятности к оцениваемому параметру при возрастании количества наблюдений. Оценка параметра называется эффективной, если она имеет наименьшую дисперсию среди возможных несмещенных оценок параметра, вычисленных по выборкам одного и того же объема n.

ГЛАВА 2. ПРОЕКТНАЯ ЧАСТЬ

2.1 Информационно-методическое обеспечение эконометрического исследования.

Методика эконометрического исследования включает следующие этапы: спецификация; параметризация, верификация, дополнительное исследование.

1. Спецификация моделей уравнения парной и множественной регрессии включает анализ корреляционной зависимости зависимой переменной от каждой объясняющей переменной. По результатам анализа делается заключение о модели уравнения регрессии. В результате этапа определяется модель уравнения регрессии.

2. Параметризация уравнения парной регрессии предполагает оценку параметров регрессии и их социально-экономическую интерпретацию. Для параметризации рекомендуется использовать инструмент «Регрессия» в составе надстроек «Анализ данных» MsExcel. По результатам автоматизированного регрессионного анализа определяются параметры регрессии, также дается их интерпретация.

Верификация уравнения регрессии проводится на основе результатов автоматизированного регрессионного анализа.

Таким образом, эконометрическое исследование парной регрессии включает расчет параметров уравнений регрессии, оценку дисперсий ошибок и дисперсий параметров модели, оценку силы связи фактора с результатом с помощью коэффициента эластичности, оценку тесноты связи, оценку качества уравнения с помощью средней ошибки аппроксимации, оценку статистической надежности уравнений регрессии с помощью F-критерия Фишера.

Для построения и анализа парной регрессии из статистического ежегодника выбран список из двадцати наиболее крупных стран Европейского союза, а именно число прибывших в страну на постоянное место жительства и номинальная годовая заработная плата наемных работников.

В результате анализа необходимо установить насколько заработная плата наемных рабочих в стране влияет на количество людей, прибывших в страну на постоянное место жительство.

Рассчитывается коэффициент корреляции по формуле:

, где

Коэффициент корреляции показывает тесноту связи изучаемых явлений.

Для построения уравнения парной регрессии необходимо рассмотреть возможные уравнения регрессии:

1. линейную зависимость
2. показательную зависимость
3. квадратичную зависимость
4. кубическую зависимость

Для оценки параметров регрессий ко всем этим моделям применим метод наименьших квадратов (МНК).

Идея метода состоит в получении наилучшего приближения набора наблюдений xi, yi, i = 1,…,n линейной функцией в смысле минимизации функционала:

Для расчета параметров a и b линейной регрессии решается система уравнений относительно a и b.

из которой можно определить оценки параметров a и b.

Линейный коэффициент парной корреляции равен:

Проверяется данный коэффициент на значимость, воспользовавшись t–критерием Стьюдента.

Выдвигается гипотеза H0 о случайной природе показателя, т.е. незначимом его отличии от нуля. H0: =0

Расчет оценок дисперсий ошибок и дисперсий параметров модели осуществляется по следующим формулам:

Построению уравнения показательной кривой предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:

Параметры уравнения модели находятся по следующим формулам:

Получено линейное уравнение.

Подставляя в данное уравнение фактические значения х, можно получить теоретические результаты значения . По ним рассчитывается показатель тесноты связи – индекс корреляции.

,

Проверяется данный коэффициент на значимость, воспользовавшись t–критерием Стьюдента.

Расчет оценок дисперсий ошибок и дисперсий параметров модели осуществляется по следующим формулам:

Производится построение уравнения квадратичной кривой , произведя замену

Получается линейное уравнение

Подставляя в уравнение фактические значения х, можно получить теоретические результаты значения . По ним рассчитаем показатель тесноты связи – индекс корреляции.

,

Проверяется данный коэффициент на значимость, воспользовавшись t–критерием Стьюдента.

Расчет оценок дисперсий ошибок и дисперсий параметров модели осуществляется по следующим формулам:

Производится построение уравнения кубической кривой , произведя замену

Получается линейное уравнение

Подставляя в данное уравнение фактические значения х, можно получить теоретические результаты значения . По ним рассчитаем показатель тесноты связи – индекс корреляции.

,

Проверяется данный коэффициент на значимость, воспользовавшись t–критерием Стьюдента.

Расчет оценок дисперсий ошибок и дисперсий параметров модели осуществляется по следующим формулам:

Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения:

Коэффициент детерминации дает оценку качества построенной модели. Коэффициент детерминации характеризует долю дисперсии результирующего признака у, объясняемую регрессией, в общей дисперсии результативного признака.

Коэффициент детерминации равен квадрату индекса корреляции. Чем ближе к единице , тем лучше качество подгонки, т.е. более точно аппроксимирует у.

Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

Допустимый предел значений - не более 8-10%.

Оценка значимости уравнения регрессии осуществляется с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза о равенстве фактической и остаточной дисперсий, и следовательно, фактор x не оказывает влияния на y, т.е.

H0: Dфакт=Dост

Для этого выполняется сравнение фактического и критического (табличного) значений F-критерия Фишера. определяется из соотношения значений факторной и остаточной дисперсий:

- максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости . Уровень значимости - вероятность отвергнуть правильную гипотезу при условии, что она верна.

Если <, то отклоняется и признается статистическая значимость и надежность уравнения регрессии, иначе - принимается и делается вывод о не значимости уравнения регрессии.

В заключение формируется суждение о качестве уравнения регрессии.

3. Параметризация уравнения множественной регрессии предполагает оценку параметров регрессии и их социально-экономическую интерпретацию. Для параметризации рекомендуется использовать инструмент «Регрессия» в составе надстроек «Анализ данных» MsExcel. По результатам автоматизированного регрессионного анализа определяются параметры регрессии, также дается их интерпретация.

Верификация уравнения регрессии проводится на основе результатов автоматизированного регрессионного анализа.

Таким образом, эконометрическое исследование множественной регрессии включает в себя построение уравнения множественной регрессии, расчет коэффициентов эластичности для каждого фактора и сравнительную оценку силы связи каждого фактора с результатом, экономическую интерпретацию построенной модели, построение матрицы корреляции, вычисление коэффициента множественной корреляции, расчет оценок дисперсий ошибок модели и оценок параметров модели, построение доверительных интервалов для коэффициентов модели с выбранным уровнем значимости, проверку значимости каждого коэффициента, оценку тесноты связи, оценку статистической надежности уравнения регрессии с помощью F – критерия Фишера.

Для построения и анализа множественной регрессии вводятся в модель еще несколько показателей, позволяющих учитывать несколько факторов, влияющих на число прибывших в страну на постоянное место жительства. А именно такие факторы как число безработных и ВВП страны.

Множественная регрессия – уравнение связи с несколькими неизвестными переменными:

,

где y – зависимая переменная (результативный признак),

- независимые переменные (факторы).

Для построения уравнения множественной регрессии используется линейная функция, записанная в матричной форме:

,

где , , ,

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов:

.

Строится следующая система уравнений, решение которых позволяет получить оценки параметров регрессии:

.

Ее решение в явном виде обычно записывается в матричной форме, иначе оно становится слишком громоздким.

Оценки параметров модели в матричной форме определяются выражением:

,

X – матрица значений объясняющих переменных;

Y – вектор значений зависимой переменной.

Для выявления зависимости числа прибывших на постоянное место жительства от номинальной годовой з/п наемных рабочих, числа безработных и уровня ВВП построим уравнение множественной регрессии в виде:

Для характеристики относительной силы влияния факторов на y рассчитаем средние коэффициенты эластичности. Средние коэффициенты эластичности для линейной регрессии рассчитываются по формулам:

.

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

где - определитель матрицы парных коэффициентов корреляции;

- определитель матрицы межфакторной корреляции.

Матрица парных коэффициентов корреляции:

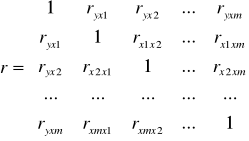
Матрица межфакторной корреляции:

Расчет оценок дисперсий ошибок и дисперсий параметров модели осуществляется по следующим формулам:

Для оценки статистической значимости коэффициентов регрессии рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из параметров. Выдвигается гипотеза о случайной природе показателей, т.е. о незначимом их отличии от нуля. Получим набор гипотез:

: b0 =0;b1 =0;b2 =0;b3 =0

Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента проводится путем сопоставления их значений с табличным значением , вычисляемым как квантиль распределения Стьюдента, где уровень значимости - вероятность отвергнуть правильную гипотезу при условии, что она верна.

Для расчета доверительных интервалов пользуются следующей формулой:

.

Качество построенной модели в целом оценивает коэффициент детерминации. Коэффициент множественной детерминации рассчитывается, как квадрат индекса множественной корреляции: .

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:

где n – число наблюдений;

m – число факторов.

Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия Фишера:

При этом выдвигается гипотеза о незначимости уравнения регрессии:

В заключение формируется суждение о качестве уравнения регрессии.

4. Проводится сравнительный анализ моделей регрессии.

2.2. Пример эконометрического исследования.

На основе статистических данных проводится эконометрическое исследования в соответствие с методикой п.2.1.

Все необходимые расчеты проводятся при помощи MS Excel, рассчитывая в ручную, при помощи функций пакета анализа данных «Регрессия» проводится проверка полученных результатов.

1. Необходимо рассчитать коэффициент корреляции.

Линейный коэффициент парной корреляции равен:

= 0,504652547

Коэффициент корреляции имеет положительное значение и равен , умеренная прямая зависимость между показателем y и фактором x: с увеличением среднегодовой з/п работников страны, количество прибывшего в страну населения увеличивается.

2. Проводится построение и анализ парной регрессии. Исходные данные представлены в Таблице 1.

Таблица 1. Исходные данные для построения и анализа парной регрессии

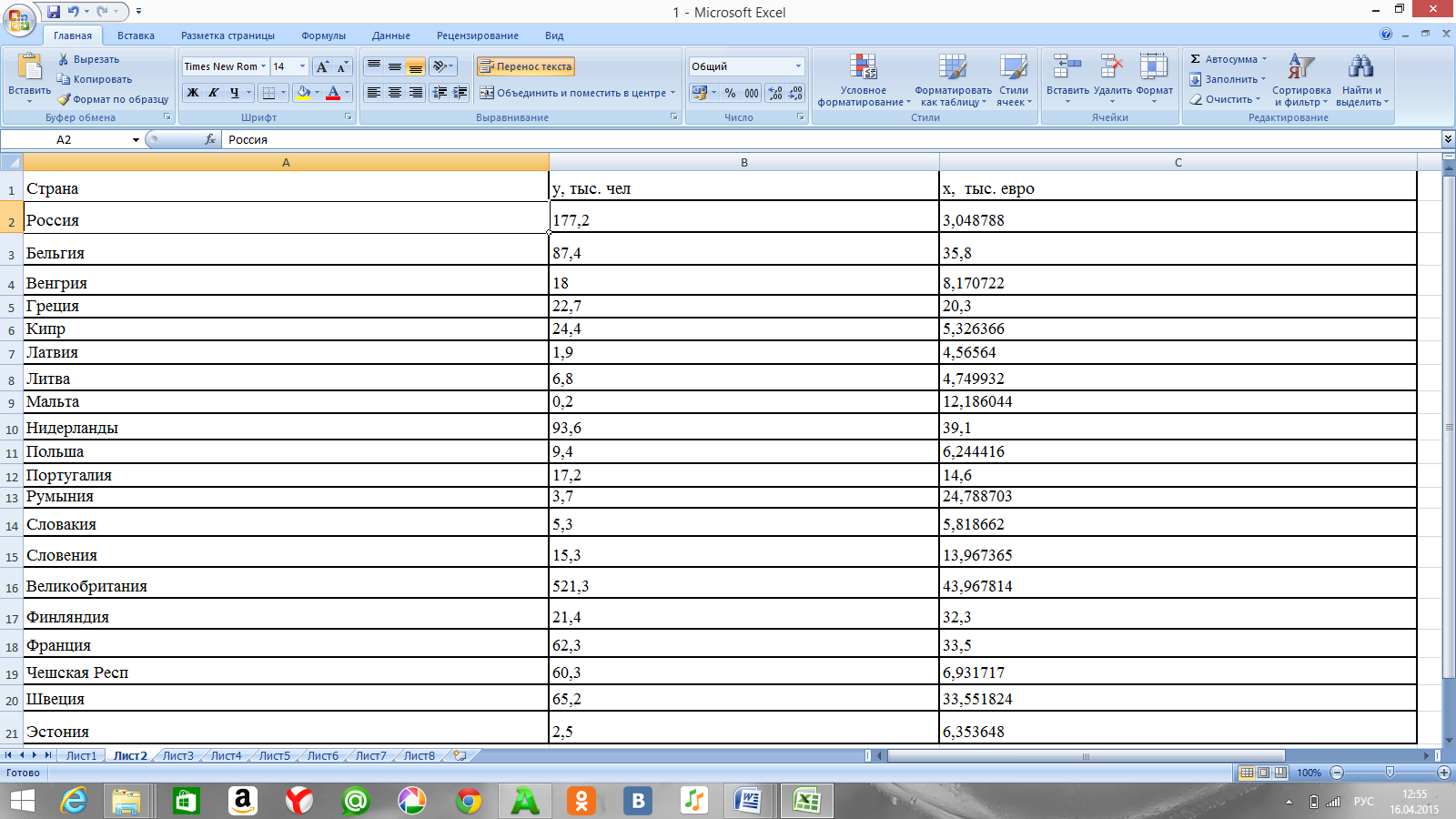
y - число прибывших в страну на постоянное место жительства, тыс. чел;

x - номинальная годовая заработная плата наемных работников, тыс. евро.

В результате анализа необходимо установить насколько заработная плата наемных рабочих в стране влияет на количество людей, прибывших в страну на постоянное место жительство.

Оценка параметров a и b.

;

Уравнение регрессии:

Коэффициент регрессии b=4,279 показывает среднее изменение результата с изменением фактора на одну единицу: с увеличением годовой з/п наемных рабочих на 1 тыс.евро. количество прибывших на постоянное место жительства увеличится в среднем на 4,279 тыс. чел. Положительное значение коэффициента регрессии показывает прямое направление связи.

Линейный коэффициент парной корреляции равен:

= 0,504652547

Связь прямая и умеренная. Проверяется данный коэффициент на значимость.

=2.47 Tтабл(0,05;18) = 2,101

> Tтабл, коэффициент значим.

Проводится расчет оценок дисперсий ошибок и дисперсий параметров модели. Промежуточные расчеты представлены в Таблице 2.

В результате получены следующие значения:

= 10765,218 = 1477,566815 = 2,976774696

Построение уравнения показательной кривой.

Значения параметров регрессии составили

= 0,068027 = 1,68049

Получено линейное уравнение: .

После потенцирования:

Индекс корреляции.

Проверяется данный коэффициент на значимость.

=2.15 Tтабл(0,05;18) = 2,101

> Tтабл, коэффициент значим.

Проводится расчет оценок дисперсий ошибок и дисперсий параметров модели. Промежуточные расчеты представлены в Таблице 3.

В результате получены следующие значения:

= 11483,75 = 452,87517 = 3,1754617

Таблица 2. Расчет значений для линейной модели

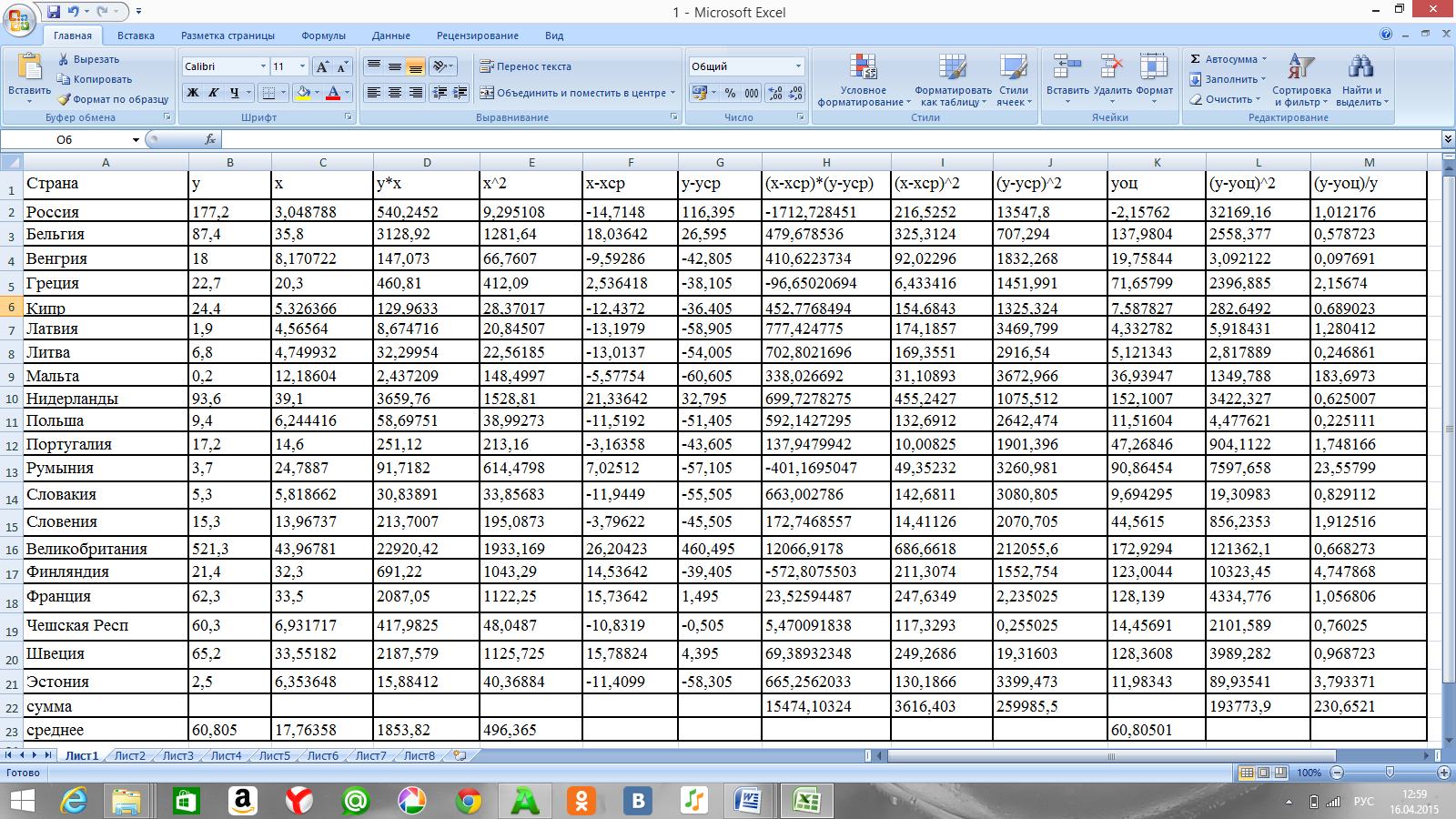
Таблица 3. Расчет значений для показательной модели

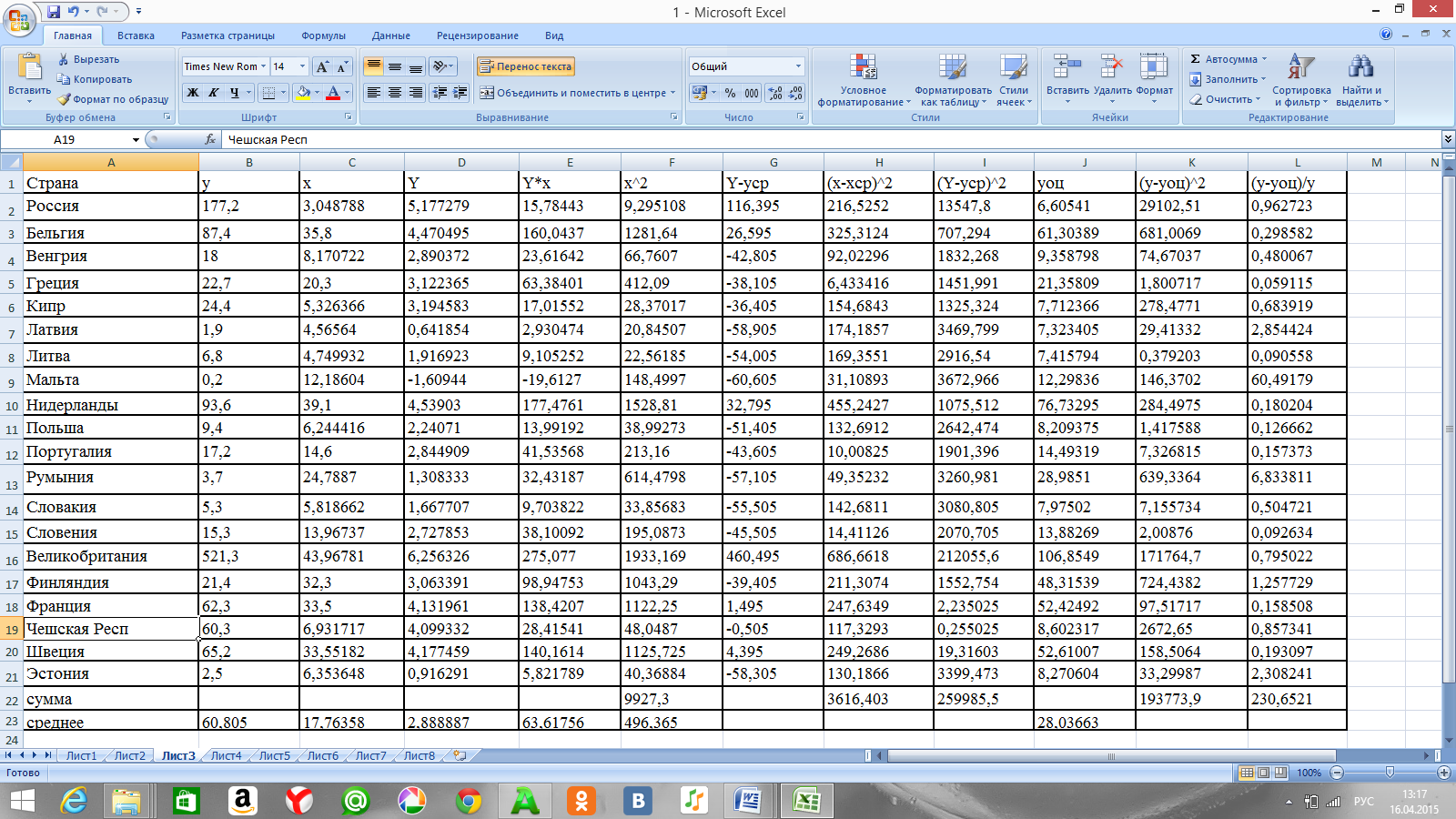
Строится уравнение квадратичной кривой.

Параметры уравнения:

Уравнение регрессии принимает вид:

Индекс корреляции.

Проверяется данный коэффициент на значимость.

=3,41 Tтабл(0,05;18) = 2,101

> Tтабл, коэффициент значим.

Проводится расчет оценок дисперсий ошибок и дисперсий параметров модели. Промежуточные расчеты представлены в Таблице 4.

В результате получены следующие значения:

= 8760,35808 = 743,283328 = 0,00123901

Строится уравнение кубической кривой.

Параметры уравнения:

Уравнение регрессии принимает вид:

Индекс корреляции.

Проверяется данный коэффициент на значимость.

=4,38 Tтабл(0,05;18) = 2,101

> Tтабл, коэффициент значим.

Проводится расчет оценок дисперсий ошибок и дисперсий параметров модели. Промежуточные расчеты представлены в Таблице 5.

В результате получены следующие значения:

= 6978,45007 = 514,7649432 = 5,9851E-07

Самая высокая степень связи переменных в модели с кубической зависимостью, т.к. коэффициент корреляции в кубической модели наиболее близок к единице, а самая низкая - в показательной модели. Дисперсии ошибок и параметров модели принимают минимальные значения в кубической.

Таблица 4. Расчет значений для квадратичной модели

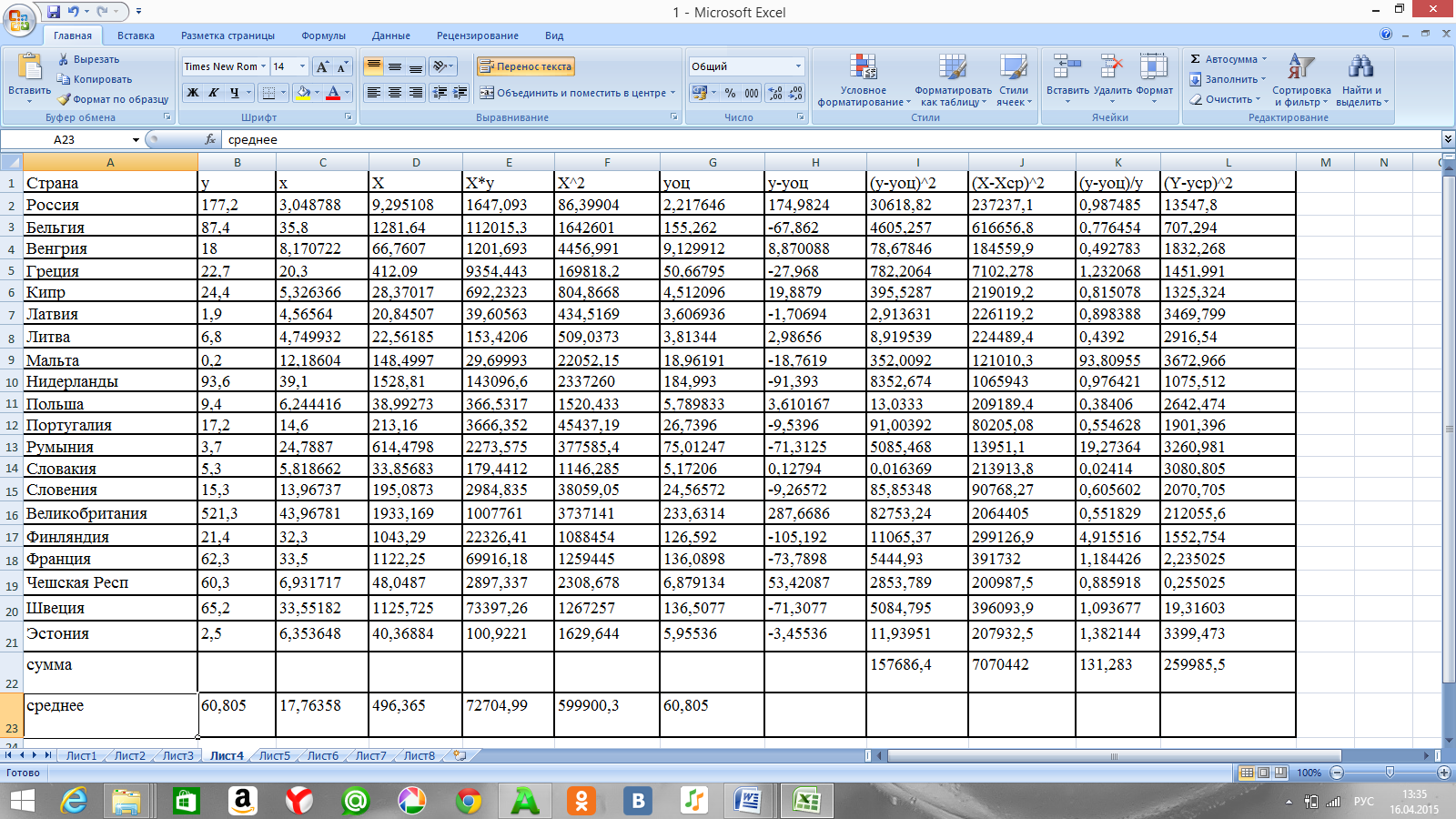
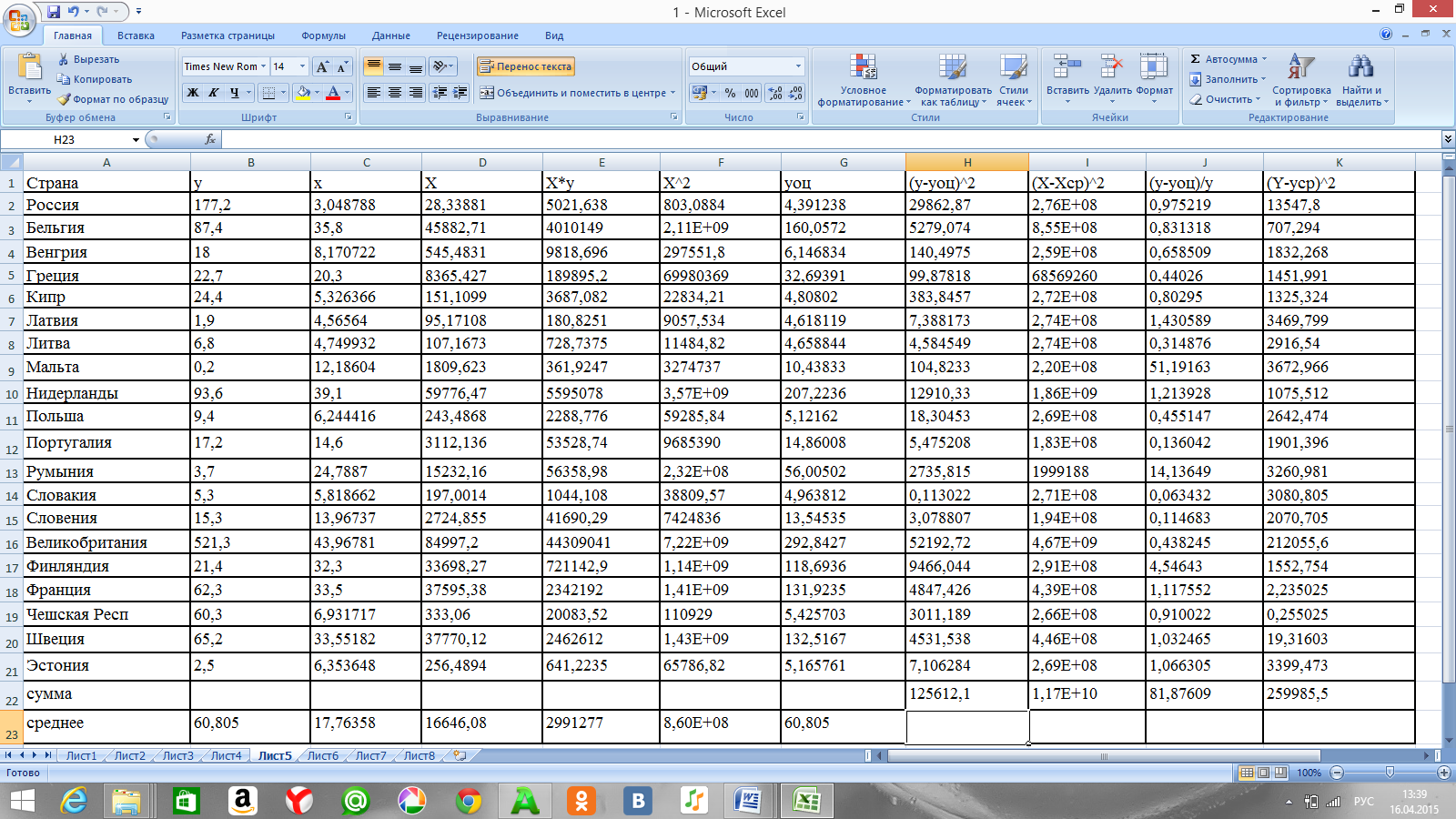
Таблица 5. Расчет значений для кубической модели

Находится средний коэффициент эластичности.

Линейная зависимость

С ростом годовой заработной платы наемных рабочих на 1% число прибывших в страну на постоянное место жительства увеличивается на 1,250028395 %.

Показательная зависимость

1,2083965

С ростом годовой заработной платы наемных рабочих на 1% число прибывших в страну на постоянное место жительства увеличивается на 1,2083965 %.

Квадратичная зависимость

С ростом годовой заработной платы наемных рабочих на 1% число прибывших в страну на постоянное место жительства увеличивается на 1,24843054 %.

Кубическая зависимость

0,938829224

С ростом годовой заработной платы наемных рабочих на 1% число прибывших в страну на постоянное место жительства увеличивается на 0,938829224 %.

Значения коэффициентов эластичности приведены в Таблице 6.

Все построенные модели подтверждают, что величина заработной платы наемных рабочих является фактором увеличения числа прибывших в страну на постоянное место жительства. Коэффициент эластичности показывает, что годовая заработная плата наемных рабочих в больше степени влияет на число прибывших в страну на постоянное место жительства при линейной и квадратичной зависимостях. В меньшей степени данная связь прослеживается в кубической зависимости.

Находится коэффициент детерминации.

Линейная зависимость

Уравнением регрессии объясняется 25% дисперсии результативного признака, а на долю остальных факторов приходится 75% ее дисперсии.

Модель линейной зависимости плохо аппроксимирует исходные данные.

Показательная зависимость =

Зависимость между показателями такая же слабая, как и в линейной модели. Вариация у всего на 20% объясняется вариацией х, а на долю остальных факторов приходится 80%. Связь в данной модели самая слабая. Поэтому качество модели неудовлетворительное.

Квадратичная зависимость

Зависимость между показателями немного лучше, чем в показательной и линейной моделях. Вариация у только на 40% объясняется вариацией х. Данную модель также не желательно использовать для прогнозирования.

Кубическая зависимость

Зависимость между показателями лучше, чем в предыдущих моделях. Вариация у на 52% объясняется вариацией х.

Значения коэффициентов детерминации представлены в Таблице 6.

Таблица 6. Расчет параметров и характеристик моделей.

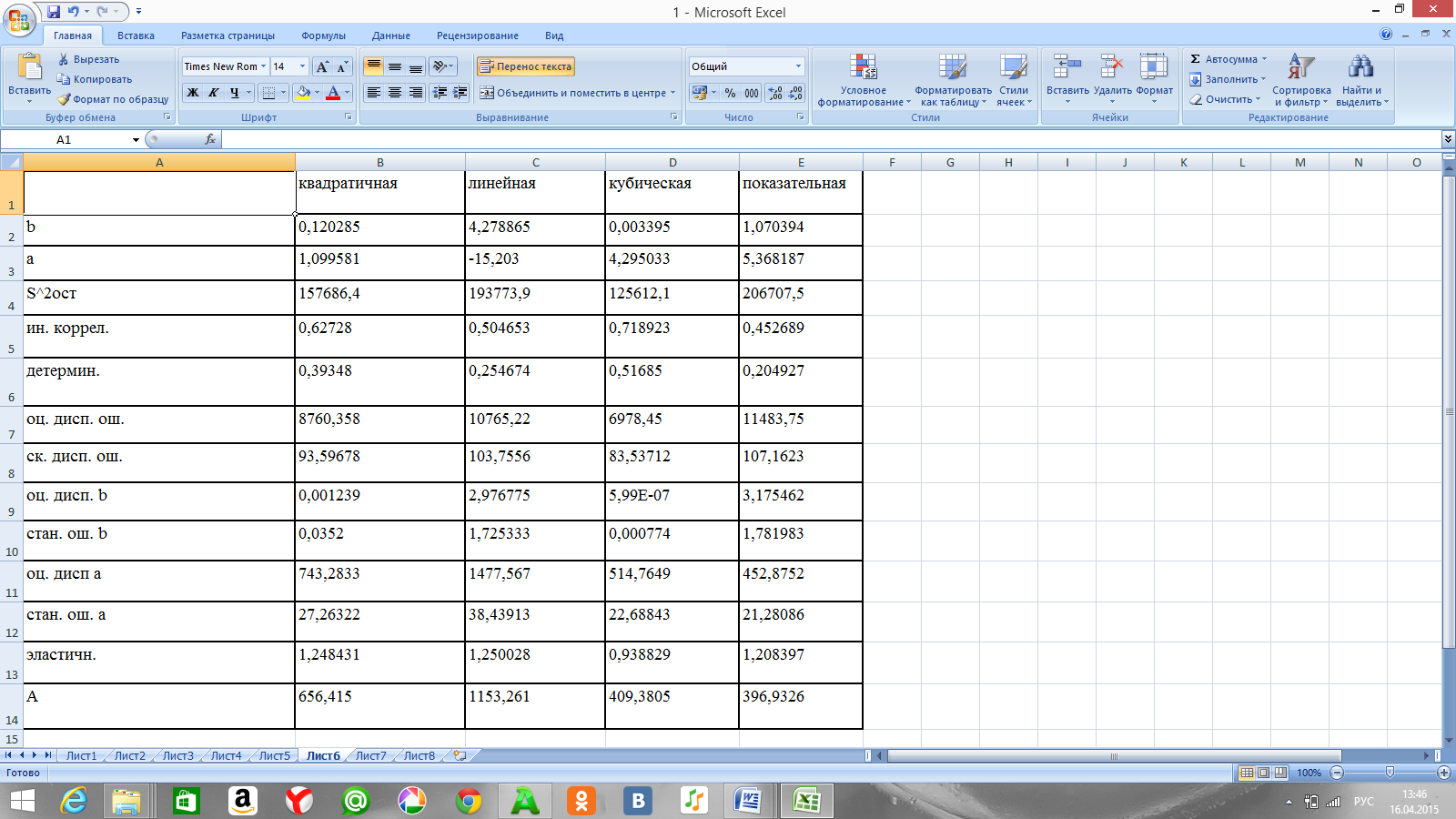
Качество построенных моделей низкое, самая высокая оценка качества у модели с кубической зависимостью, так как доля объясненной вариации составила 52%.

Определяется средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

Линейная модель =1153,261%

В среднем расчетные значения отклоняются от фактических на 1153,261%, что говорит об очень большой ошибке аппроксимации.

Показательная зависимость =396,93259

Ошибка аппроксимации несколько ниже, чем у остальных моделей, но также является недопустимой.

Квадратичная зависимость =656,415018

Наблюдается высокая ошибка аппроксимации, что свидетельствует о низком качестве подгонки уравнения

Кубическая зависимость =409,3804652

Ошибка аппроксимация также значительно превышает допустимые значения. Во всех рассмотренных моделях средняя ошибка аппроксимации значительно превышает допустимые значения, качество подгонки моделей к исходным данным очень низкое.

3. Проводится построение и анализ множественной регрессии.

Исходные данные для построения множественной регрессии приведены в Таблице 7.

Таблица 7. Исходные данные для построения множественной регрессии.

y- число прибывших в страну на постоянное место жительства, тыс. чел:

x1- номинальная годовая заработная плата наемных работников, тыс. евро.

x2- число безработных, тыс. чел.

x3- ВВП, млрд. евро.

Оценки параметров уравнения регрессии:

Уравнение множественной регрессии:

Средние коэффициенты эластичности.

= 0,12026241 = -0,06319176 = 0,86930458

Расчет данных значений приведен в Таблице 8.

С увеличением величины годовой заработной платы наемных рабочих на 1% от среднего уровня при неизменных показателях остальных факторов, число прибывших на постоянное место жительства увеличивается на 0,12%.

С увеличением численности безработных на 1% от среднего при неизменных показателях остальных факторов, число прибывших на постоянное место жительства уменьшается на 0,06%

С увеличением величины ВВП на 1% от среднего при неизменных показателях остальных факторов, число прибывших на постоянное место жительства увеличивается на 0,87%

Изменение числа прибывших в страну на постоянное место жительства находится в прямой зависимости от годовой заработной платы наемных рабочих и величины уровня ВВП страны и в обратной зависимости от численности безработных, что не противоречит и логическим предположениям. Коэффициенты эластичности, как показатели силы связи, показывают, что наибольшее изменение числа прибывших в страну вызывает величина ВВП, а наименьшее – численность безработных.

Рассчитывается коэффициент множественной корреляции:

Значение индекса множественной корреляции лежит в пределах от 0 до 1.

Рассчитывается средняя ошибка аппроксимации:

= 372,353247%

Значение средней ошибки аппроксимации свидетельствует о плохой подгонке модели под исходные данные.

Таблица 8. Расчет значений характеристик модели множественной регрессии

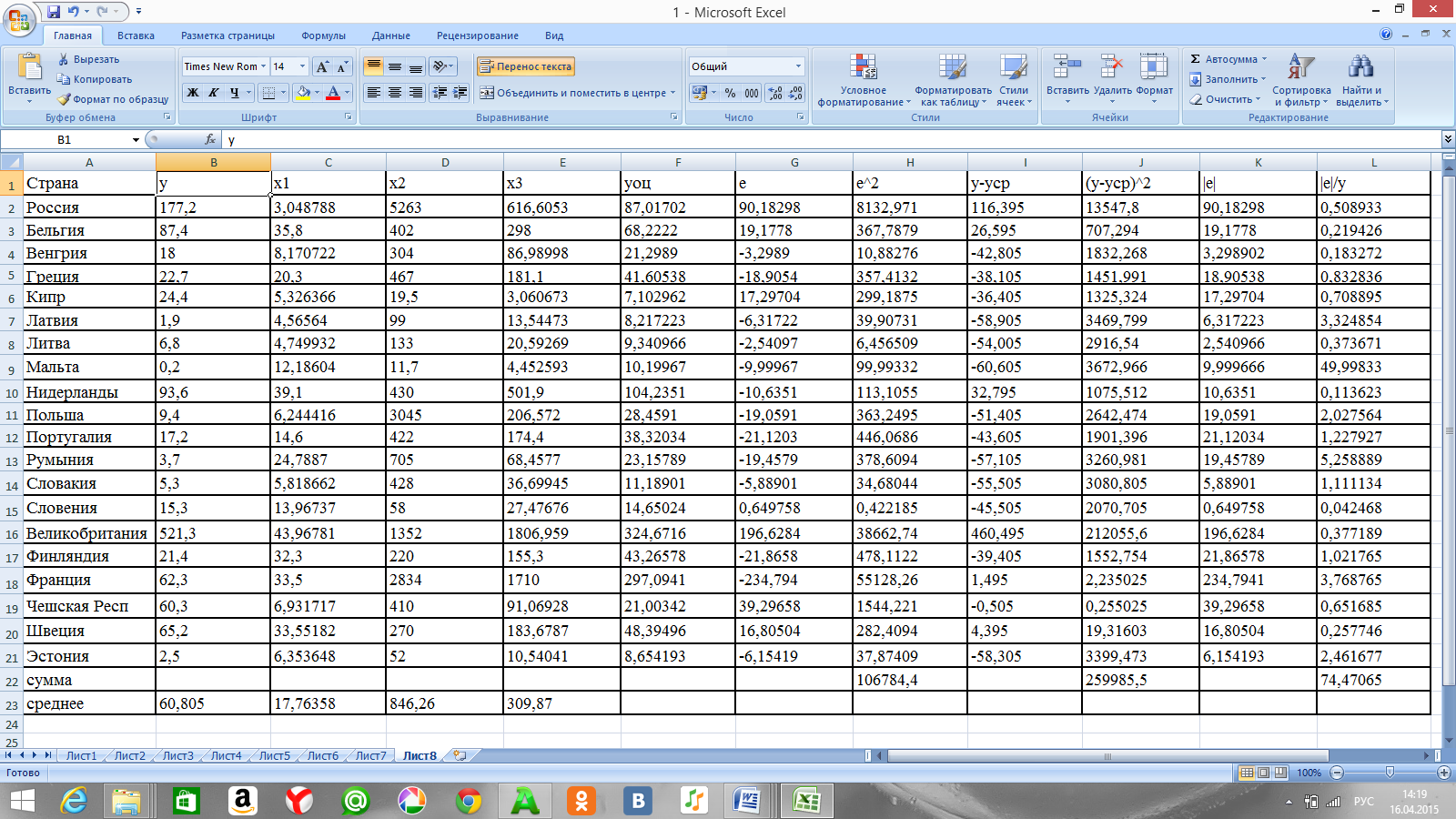
Совместное влияние всех факторов на число прибывших в страну на постоянное место жительства достаточно велико. Связь между рассматриваемым показателем и влияющими на него факторами усилилась по сравнению с парной регрессией (ryx=0.506). Наблюдается довольно сильная связь.

Необходимо учитывать, что в модели наблюдается небольшая мультиколлинеарность, что может свидетельствовать о ее неустойчивости, поскольку определитель матрицы межфакторной корреляции достаточно далек от 1. Максимальный коэффициент парной корреляции наблюдается между факторами x1 и x3 (rx1x3=0.595), что вполне объясняемо, т.к. среднегодовая заработная плата в стране должна находиться в прямой зависимости от ВВП страны.

Расчет оценок дисперсий ошибок и дисперсий параметров модели:

n = 20 – количество наблюдений, m=4 – количество параметров.

Для построенной модели оценка дисперсии ошибок составила:

=6674,02207

Оценки дисперсий параметров модели:

Стандартные ошибки параметров модели:

Промежуточные расчеты полученных данных представлены в приложении 8.

Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента.

,

,

Значения , , <, значит коэффициенты являются статистически незначимыми и случайно отличаются от 0.

>, значит является статистически значимым

Для построенной модели доверительные интервалы коэффициентов регрессии:

Все полученные коэффициенты регрессии, кроме , статистически незначимы, доверительные интервал для них достаточно большой, что может свидетельствовать о недостаточном качестве модели.

Коэффициент множественной детерминации для построенной модели

Данный коэффициент детерминации показывает, что качество модели удовлетворительное.

С добавлением еще одной переменной обычно увеличивается. Для того чтобы не допускать возможного преувеличения тесноты связи и применяется скорректированный коэффициент детерминации. При заданном объеме наблюдений при прочих равных условиях с увеличением числа независимых переменных (параметров) скорректированный коэффициент множественной детерминации убывает. Для построенной модели значения скорректированного и нескорректированного коэффициента детерминации не значительно отличаются друг от друга, но т.к. скорректированный коэффициент детерминации немного уменьшился можно предположить, что увеличение доли объясненной регрессии при добавлении новой переменной незначительно, и что добавлять переменную нецелесообразно.

Оценка значимости уравнения регрессии с помощью F-критерия Фишера.

= F (0.05,m-1,n-m)= F(0.05,1,18)= 4,413873

Линейная модель =6,150512218

Показательная зависимость =4,6394274

Квадратичная зависимость =11,6775003

Кубическая зависимость =19,25548322

Во всех рассмотренных моделях <, гипотеза отвергается.

Значимость уравнения множественной регрессии в целом с помощью F-критерия Фишера:

Так как Fтабл< Fфакт то не принимается

4. В результате проведенного исследования можно сделать следующее заключение: Все полученные уравнения регрессии значимы. По результатам F-теста и показателям коэффициента детерминации и средней ошибки аппроксимации можно сделать вывод, что среди рассмотренных моделей парной регрессии нет модели с хорошим качеством, которую можно было бы применять с целью прогнозирования. Однако, наилучшей моделью, описывающей взаимосвязь между годовой з/п наемных рабочих страны и числом прибывших в страну на постоянное место жительства, является модель с кубической зависимостью, поскольку она является значимой, коэффициент детерминации принимает наибольшее значение и средняя ошибка аппроксимации не так велика по сравнению с другими моделями, хотя и не принимает допустимого значения.

Все четыре модели парной регрессии являются статистически значимыми, однако достаточно малые значения коэффициента детерминации, большие ошибки средней аппроксимации свидетельствуют о плохом качестве данных моделей.

Сравнив параметры и характеристики данных уравнений, делается вывод, что наибольшей надежность и точностью обладает модель с кубической зависимостью. Об этом свидетельствуют наибольшее значение индекса корреляции и соответственно коэффициент детерминации, наиболее близкий к 1 и подтверждающий лучшее качество модели с точки зрения аппроксимации данных, результаты F-теста, признавшие модель значимой, а также средняя ошибка аппроксимации, меньшая, чем у других моделей. Стандартные ошибки параметров регрессии и стандартная ошибка прогноза для этой модели также принимают меньшие значения.

Уравнение множественной регрессии значимо, т.е. отвергается гипотеза о случайной природе оцениваемых характеристик. Полученная модель статистически надежна.

ЗАКЛЮЧЕНИЕ

В результате эконометрического исследования и анализа данных было рассмотрено четыре уравнения парной регрессии, устанавливающих зависимость между среднегодовой заработной платой наемных рабочих в стране и количеством людей, прибывших в страну на постоянное место жительство. Это линейная модель, показательная, модели с квадратичной и кубической зависимостью. Все построенные модели подтверждают, что рост величины заработной платы наемных рабочих, является фактором увеличения числа прибывших в страну на постоянное место жительства.

Самый высокий показатель тесноты связи переменных в модели с кубической зависимостью, т.к. коэффициент детерминации в кубической модели принимает наибольшее значение, что говорит о наибольшей надежности найденного уравнения регрессии. Модель в виде кубической зависимости наилучшим образом описывает взаимосвязь числа прибывших в страну на постоянное место жительства и годовой заработной платы наемных рабочих. Во всех рассмотренных моделях средняя ошибка аппроксимации значительно превышает допустимые значения, что говорит о низком качестве подгонки моделей. Однако модель с кубической зависимостью является лучшей с точки зрения аппроксимации данных и оценки тесноты связи, поскольку имеет наибольшую по сравнению с другими моделями долю объясненной вариации – 52% (коэффициент детерминации наиболее близок к 1).

По всем рассмотренным параметрам, уравнение регрессии с кубической зависимостью, является лучшим из рассмотренных. Но не оптимальным для практического использования и прогнозирования, что объясняется большим разбросом данных, а также тем, что число иммигрантов зависит от множества факторов, которые невозможно учесть в парной регрессии.

Не достаточно хорошие характеристики модели могут быть вызваны наличием в исходных данных единиц с аномальными значениями исследуемых признаков: в Великобритании число прибывших на постоянное место жительства значительно превышает данный показатель для других стран. Возможно, для получения более точного и надежного результата данную страну следует исключить из выборки.

В результате построения множественной регрессии исследовано влияние на число прибывших в страну на постоянное место жительства таких факторов, как ВВП страны, численность безработных и средняя годовая заработная плата наемных рабочих.

Изменение числа прибывших в страну на постоянное место жительства находится в прямой зависимости от годовой заработной платы наемных рабочих и величины уровня ВВП страны и в обратной зависимости от численности безработных. Наибольшее изменение числа прибывших в страну вызывает величина ВВП, а наименьшее – численность безработных.

Совместное влияние всех факторов на число прибывших в страну на постоянное место жительства достаточно велико, поскольку индекс множественной корреляции принимает высокое значение. Однако это может объясняться наличием мультиколлинеарности.

Все полученные коэффициенты уравнения множественной регрессии кроме коэффициента при факторе уровень ВВП статистически незначимы, доверительные интервал для них достаточно большой.

Не смотря на это, коэффициент детерминации показывает, что качество модели удовлетворительное. Уравнение множественной регрессии значимо, т.е. отвергается гипотеза о случайной природе оцениваемых характеристик.

Однако в модели может наблюдаться гетероскедастичность, т.е. возможно необходима коррекция модели.

Данные результаты можно объяснить достаточно малым объемом выборки, в особенности с учетом глобальности исследования, наличием аномального значения исследуемого признака, не учтенностью каких-либо существенных факторов, а также тем, что число эмигрантов в страну зависит от большого числа не количественных, личных факторов, индивидуальных предпочтений.

Не смотря на отсутствие точного результата и качественного уравнения регрессии, пригодного для прогнозирования и дальнейших исследований, в ходе исследования удалось выявить, что заработная плата наемных рабочих в стране, уровень безработицы и ВВП оказывают немаловажное влияние на число прибывших в страну на постоянное место жительства.

Список использованных источников

1. Герасимов, А.Н. Эконометрика: теория и практика [Электронный ресурс]: электронный учебник / Герасимов, А.Н., Гладилин, А.В., Громов, Е.И. - М.: КноРус, 2011. - CD. - (82803-2) (У; Г 37)

2. Яковлева, А. Заказ. Эконометрика: курс лекций - М.: Эксмо, 2010. - (83407-1)

3. Валентинов, В.А. Эконометрика [Текст]: практикум - М.: Дашков и К, 2010. - 435 с. - (84265-12) (У; В 15)

4. Валентинов, В.А. Эконометрика [Текст]: учебник для вузов по спец. "Мат. методы в экономике" и др. экон. спец. - М.: Дашков и К, 2010. - 448 с. - (84266-30) (У; В 15)

5. Новиков, А.И. Эконометрика [Текст]: учеб. пособие для вузов по направлению 521600 "Экономика" и экон. специальностям - М.: ИНФРА-М, 2011. - 143, [1] с. - (86112-10) (У; Н 73)

6. Колемаев, В.А. Эконометрика [Текст]: учебник для вузов по специальности 061800 "Математические методы в экономике" / Гос. ун-т упр. - М.: ИНФРА-М, 2010. - 160 с. - (86113-10) (У; К 60)

7. Гладилин, А.В. Эконометрика [Текст]: учеб. пособие для вузов по экон. специальностям / Гладилин, А.В., Герасимов, А.Н., Громов, Е.И. - М.: КноРус, 2011. - 227 с. - (86160-10) (У; Г 52)

8. Новиков, А.И. Эконометрика [Текст]: учеб. пособие по напр. "Финансы и кредит", "Экономика" - М.: Дашков и К, 2013. - 223 с. - (93895-1) (У; Н 73)

9. Тимофеев, В.С. Эконометрика [Текст]: учебник для бакалавров по экон. напр. и спец. / Тимофеев, В.С., Фаддеенков, А.В., Щеколдин, В.Ю. - М.: Юрайт, 2013. - 328 с. - (94305-3) (У; Т 41)

10. Эконометрика [Текст]: учебник для магистров, для вузов по экон. направления и спец. / Елисеева, И.И., Курышева, С.В., Нерадовская, Ю.В., [и др.] ; под ред. И.И. Елисеевой; Санкт-Петербургский гoс. ун-т экономики и финансов - М.: Юрайт, 2012. - 449 с. - (95469-2) (У; Э 40)

11. Новиков, А.И. Эконометрика [Электронный ресурс]: учеб. пособие - М.: Дашков и К, 2013. - ЭБС Лань. - (104974-1) (У; Н 73)

12. Варюхин, А.М. Эконометрика [Текст]: конспект лекций / Варюхин, А.М., Панкина, О.Ю., Яковлева, А.В. - М.: Юрайт, 2007. - 191 с. - (105626-1) (У; В 18)

13. Эконометрика [Электронный ресурс]: учебник / Балдин, К.В., Башлыков, В.Н., Брызгалов, Н.А., [и др.] ; под ред. В.Б. Уткина - Москва: Дашков и К, 2013. - ЭБС Лань. - (107123-1) (У; Э 40)

14. Перепелица, Н.М. *Эконометрика : практикум (направление 100700.62 Торговое дело) [Электронный ресурс]: в составе учебно-методического комплекса / Тверской гос. техн. ун-т, Каф. МЕН - Тверь: ТвГТУ, 2012. - Сервер. - (107926-1)

EMBED Equation.3

Сравнительный анализ эконометрических моделей регрессии