Расчет на прочность балки с жесткозаделанным левым и свободно опертым правым концом, нагруженной на части длины равномерной нагрузкой
АННОТАЦИЯ
В представленной работе выполнен расчет на прочность балки с жесткозаделанным левым и свободно опертым правым концом, нагруженной на части длины равномерной нагрузкой. Методом начальныхпараметров получены выражения для вычисления прогиба, угла поворота, изгибающегомомента и перерезывающей силы точек оси балки. Для получения численных значенийискомых величин по этим выражениям проведён расчёт и построены эпюры исследуемыхвеличин средствами электронных таблиц Microsoft Excel и математического пакетаMathCad. Также составлена программа на языке программирования Visual Basic.
Работа содержит 26 страниц и 18 рисунков.
THE SUMMARY
In given work the account beam, with rigidly closed up left end and freely baseright end loaded on part of length with uniform loading is executed. The method of initial parameters receives expressions for calculation of a deflection,corner of turn bending moment and cutting of force of points of an axis of a beam. For receptionof numerical values of required sizes on these expressions the account is carried out and isconstructed graphics dependences of researched sizes by means of spreadsheets Microsoft Exceland MathCad. Also the program on the programming language Visual Basic is made.
The work contains - pages and - drawings.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
В последнее время в инженерной практике все больше происходит внедрениекомпьютерной вычислительной техники, предопределяющей проведение различныхрасчётов. В частности – расчет балок на изгиб с использованием компьютерныхтехнологий. Компьютерная техника в данном случае значительно уменьшает время,расходуемое на выполнение вычислений, помогает избежать вычислительных ошибок ипозволяет проводить повторные расчёты. Применение табличного процессора MicrosoftExcel и автоматизированной системы MathCAD позволяет производить расчётопределяемых характеристик автоматически, а также провести построение эпюр, которыеграфически будут отображать данные.
Совокупность методов, служащих для определения внутренних сил и выбора поним прочных размеров частей сооружений и машин, составляет сущность инженернойдисциплины «Сопротивление материалов». Изучение изгиба балки представляет собойбольшую и сложную задачу, в которой немалую роль занимает этап исследованияизогнутой оси балки и определение прогибов в наиболее характерных точках.
Напряжения, возникающие в разных сечениях балки, зависят от величины изгибающего момента (М) и перерезывающей силы (Q) в соответствующих сечениях. Изгибающиймомент – это момент внешних сил относительно сечения балки. Перерезывающая сила –это сила, действующая перпендикулярно продольной оси балки.При исследовании балок нужно знать величины M и Q в любом сечении.
Изменение этих величин по всей длине балки удобнее всего представить графически. Длячего используются графики, называемые эпюрами изгибающих моментов иперерезывающих сил. Для построения эпюр используют различные методы: поопределенным реакциям, способ сложения сил, непосредственное интегрированиедифференциального уравнения изогнутой оси балки, метод начальных параметров.
Целью данной выполняемой работы является расчёт методом начальныхпараметров балки длиной l=2,5 м, выполненной из одного материала, с жёсткозаделанным левым и свободно опёртым правым концом, нагруженной на части длины гидростатической нагрузкой q=20 кН, с=0,5 м.
1.МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ ПРИ РАСЧЕТЕ БАЛКИ НАИЗГИБ
В качестве исходного уравнения метода начальных параметров принимаетсядифференциальное уравнение4-го порядка:
(1.1)
где EI – жесткость балки, – прогиб, q – нагрузка.
Это уравнение устанавливает зависимость между погибом балки v и внешнейнагрузкой q. В данном случае, возможно найти изогнутую ось балки непосредственно повиду внешней нагрузки, не прибегая к предварительному ее статистическому расчету и несоставляя выражения изгибающего момента по участкам. Решение уравнения (1.1) приметвид:
(x), (1.2) где ,- произвольные постоянные интегрирования.
Поскольку 3! = 6 и 2! = 2, получим:
(1.3)
При этом - частное решение неоднородного уравнения (1.1) - вычисляется по формуле:
. (1.4)
Сущность метода начальных параметров состоит в том, что произвольным постоянным интегрирования , , , придан физический смысл, заключающийся в том, что:
- прогиб в начале координат (х=0) есть постоянная, уменьшенная в EI раз:
-угол наклона оси балки в начале координат есть постоянная , уменьшенная в EI раз: ;
- изгибающиймомент в начале координат есть постоянная с противоположным знаком: ;
- перерезывающая сила в начале координат есть постоянная с противоположнымзнаком:.
В связи с этим введем обозначения:
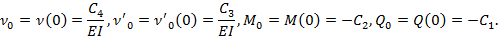
Получим выражение для определения прогиба в любой точке изогнутой балки:
(1.5)
Начало координат выбрано на левом конце балки, что обычно имеет место при проведении практических расчетов. Следовательно, указанные величины представляют прогиб, угол поворота, изгибающий момент и перерезывающую силу на левом конце балки. Последнее слагаемое в формуле (1.5) соответствует внешней нагрузке, приложенной к балке, и вычисляется в зависимости от вида нагрузки согласно теории сопротивления материалов.
Подставляя соответствующее приложенной нагрузке выражение приходим к уравнению, определяющему прогиб в любой точке оси балки с точностью до четырех начальных параметров.
Для нахождения прогиба балки необходимо найти все четыре неизвестные постоянные . Два из четырех параметров определяются сразу же изграничных условий, поставленных на левом конце балки. Для двух других начальныхпараметров необходимо сформулировать два граничных условия на другом ее конце.После определения всех четырех неизвестных постоянных, полностью найдем прогиббалки.
Первая производная по x выражения (1.5) позволяет получить выражение для углаповорота оси балки. Для вычисления изгибающего момента и перерезывающей силыиспользуются известные соотношения сопротивления материалов:
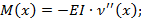
(1.6)
Т.е., для вычисления характеристик балки нужно продифференцировать выражение (1.5) для прогиба по x до третьей производной.
2. ПРИМЕНЕНИЕ МЕТОДА НАЧАЛЬНЫХ ПАРАМЕТРОВ
К ПОСТАВЛЕННОЙ ЗАДАЧЕ
Вариант 21
Задана балка, выполненная из одного материала, с жестко заделанным левым и свободно опертым правым концом, длиной l=2,5 м, нагруженная на части длины гидростатической нагрузкой q=20кН, с=0,5 м.
Рис. 2.1 Расчетная схема
Решение в общем виде выглядит:
Для рассматриваемого случая имеет вид:
(2.1)
Тогда выражение для определения прогиба запишется:
(2.2)
Чтобы получить формулы для определения величин угла поворота, изгибающего момента и перерезывающей силы, необходимо соответственно найти первую, вторую третью производные по х из выражения (2.2):
(2.3)
(2.4)
(2.5)
(2.6)
(2.7)
В данной задаче балка жестко закреплена с обоих концов. Следовательно, в начале и конце балки прогиб и угол поворота равняются нулю.
Приравняем к нулю выражения (2.2) и (2.3) при х=0:
(2.8)
(2.9)
Из уравнений (2.8) и (2.9) следует, что .
Приравниваем к нулю выражения (2.2) и (2.5) при x=l: (l)=0; (l)=0:
(2.10)
(2.11)
Подставим в уравнение (2.10) полученные выше значения =0 и =0; умножим уравнение (2.10) на EI, переносим свободные члены в правую часть и сводим данные уравнения (2.10) и (2.11) в систему:
(2.12)
Получаем систему уравнений для определения двух начальных параметров (M0, Q0).
Решив систему (2.12) и получив значения , можно вычислить все характеристики изогнутой балки: прогиб, угол поворота, изгибающий момент и перерезывающую силу, применив формулы (2.2), (2.3), (2.5), (2.7) соответственно.
3.РЕШЕНИЕ И ПОСТРОЕНИЕ ЭПЮР СРЕДСТВАМИ MS EXCEL
Для решения системы (2.12) используем матричный способ решения систем линейных уравнений. В Excel заносим в ячейки B2:В5 исходные данные для расчета (рис.3.1). В ячейках A8:B9, E8:E9 вычисляем коэффициенты и столбец свободных членов системы линейных алгебраических уравнений (2.12). Определяем обратную матрицу в диапазоне ячеек A11:B12. В ячейках Е11:Е12 вычисляем искомые значения и как результат умножения обратной матрицы на столбец свободных членов.
Рис. 3.1. Фрагмент листа Excel с исходными данными расчета в режиме отображения чисел
Рис. 3.2 Фрагмент листа Excel с решением системы уравнений (2.12) в режиме отображения формул
В ячейки A13:A24 заносятся значения координаты x, для которых будут
вычисляться смещения, угол поворота, изгибающие моменты и перерезывающая сила.
В ячейках B13:B24 вычисляется прогиб по формуле (2.2) с нормирующиммножителем EI.
В ячейках C13:C24 вычисляется угол поворота точек оси балки по формуле (2.3) снормирующим множителем EI.
В ячейках D13:D24 вычисляется изгибающий момент точек оси балки по формуле(2.5).
В ячейках E13:E24 вычисляется перерезывающая сила точек оси балки по формуле(2.7) (см. рис. 3.3).
Рис. 3.3. Фрагмент листаExcel с вычислением формул искомых величин в режиме числе
Вычисления в режиме проверки формул приведены ниже (рис. 3.4 – 3.7).
Рис. 3.4. Фрагмент листа Excel с вычислением прогиба в режиме отображения формул
Рис. 3.5. Фрагмент листа Excel с вычислением угла поворота в режиме отображения формул
Рис. 3.6. Фрагмент листа Excel с вычислением изгибающего момента в режиме отображения формул
Рис. 3.7. Фрагмент листа Excel с вычислением перерезывающей силы в режиме отображения формул
Для построения эпюр удобно воспользоваться мастером диаграмм (рис.3.8-3.11). Эпюра - это графическое изображение воздействия нагрузки.
Рис. 3.8. Эпюра прогиба оси балки
Рис. 3.9. Эпюра угла поворота оси балки
Рис. 3.10. Эпюра изгибающего момента оси балки
Рис. 3.11. Эпюра перерезывающей силы оси балки
4.РЕШЕНИЕ И ПОСТРОЕНИЕ ЭПЮР СРЕДСТВАМИ MATHCAD
Задание исходных данных:
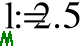
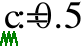
Рис. 4.1. Фрагмент листа MathCAD с заданием исходных данных
Систему линейных уравнений с квадратной матрицей удобно решать с помощью встроенной функции lsolve.
Определение коэффициентов M0 и Q0:

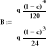
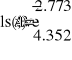
Рис. 4.2. Фрагмент листа MathCAD с решением системы
Следовательно, M0= -2,773; Q0=4.352
Средствами MathCAD вычисляем характеристики балки на изгиб (прогиб, угол поворота, изгибающий момент, перерезывающую силу) и строим эпюры (рис. 4.3 – 4.6).

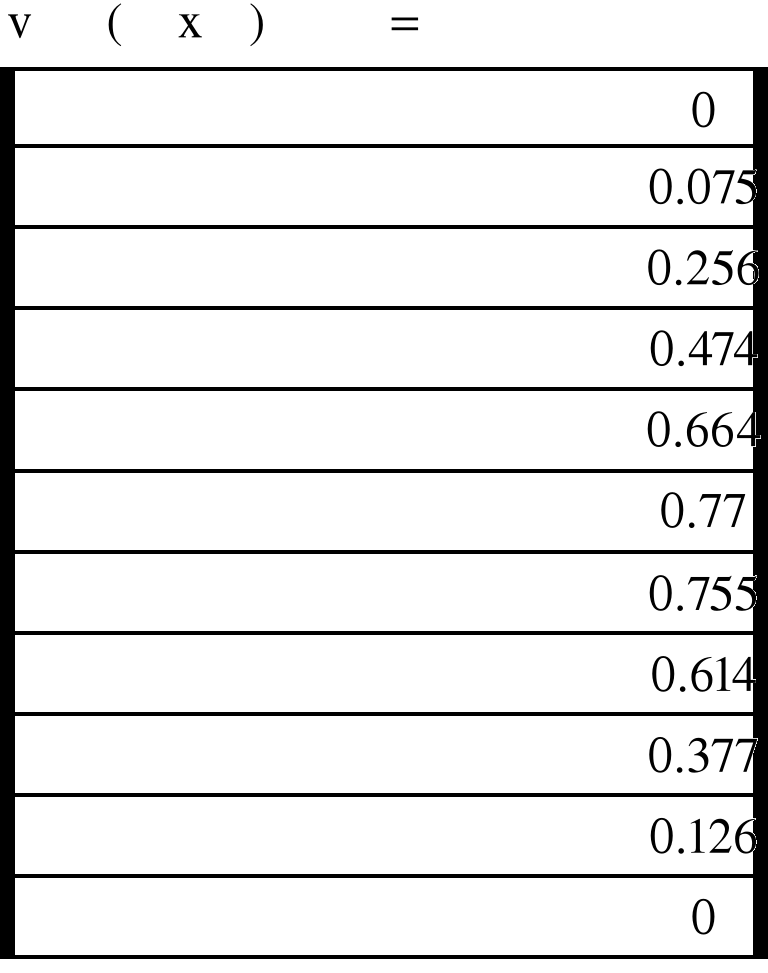
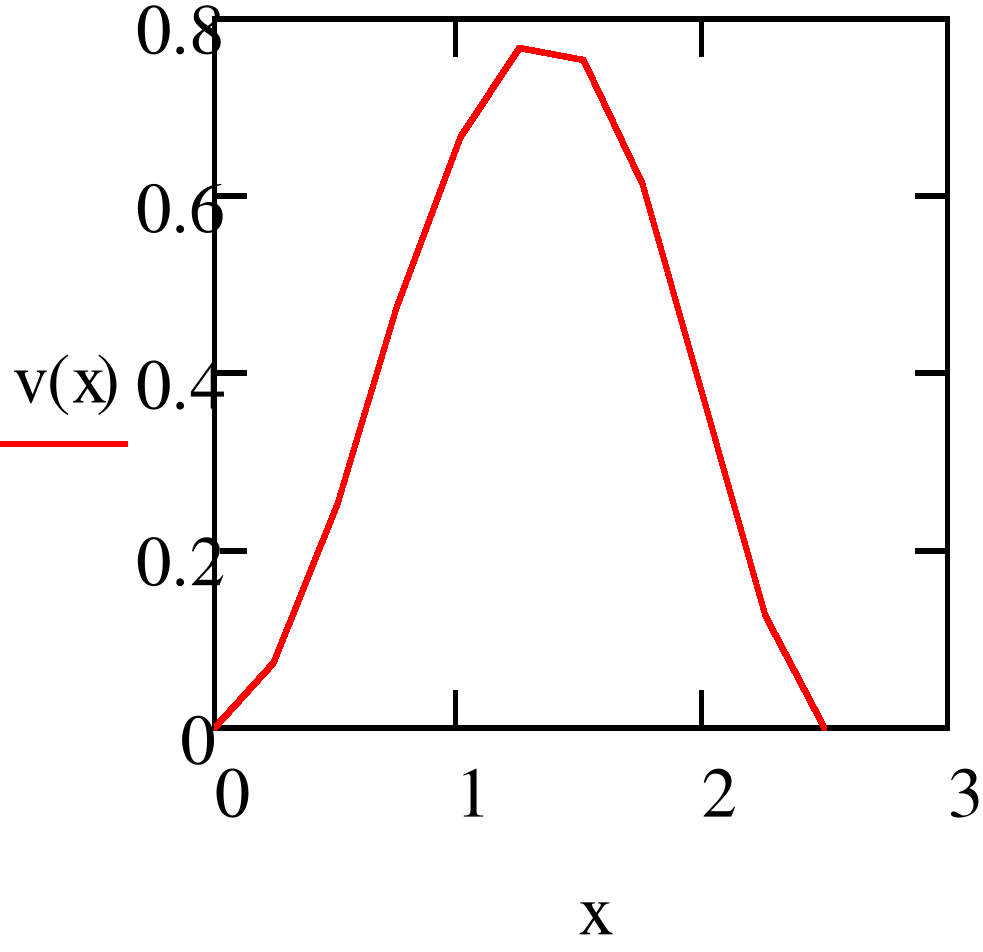
Рис.4.3.Эпюра прогиба оси балки
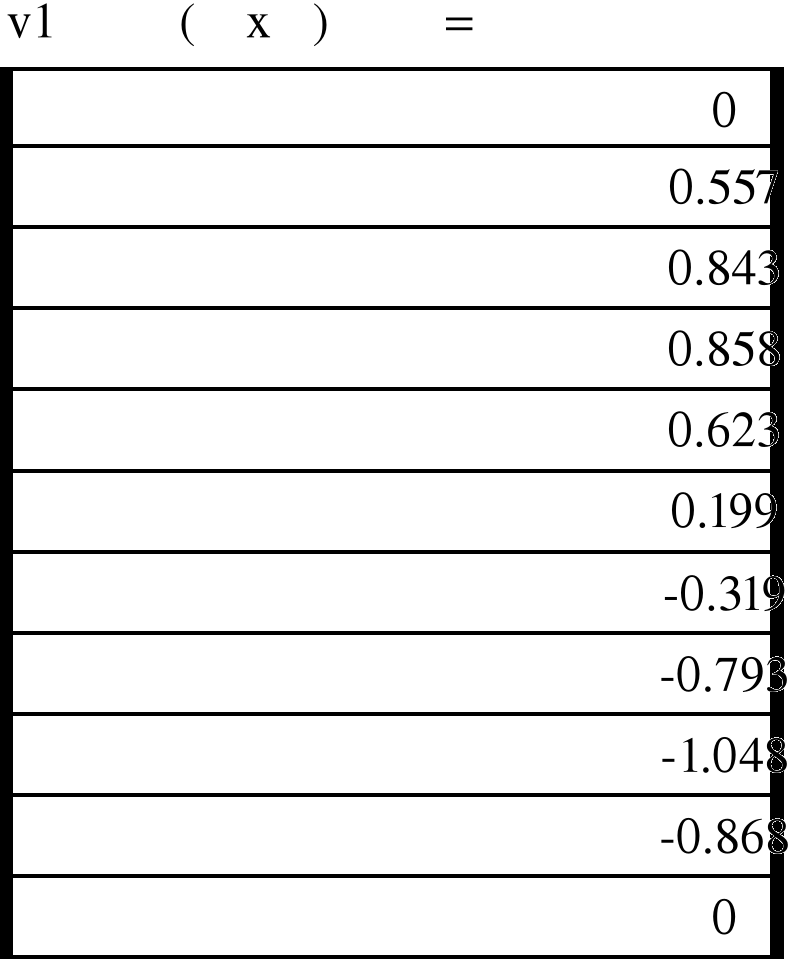
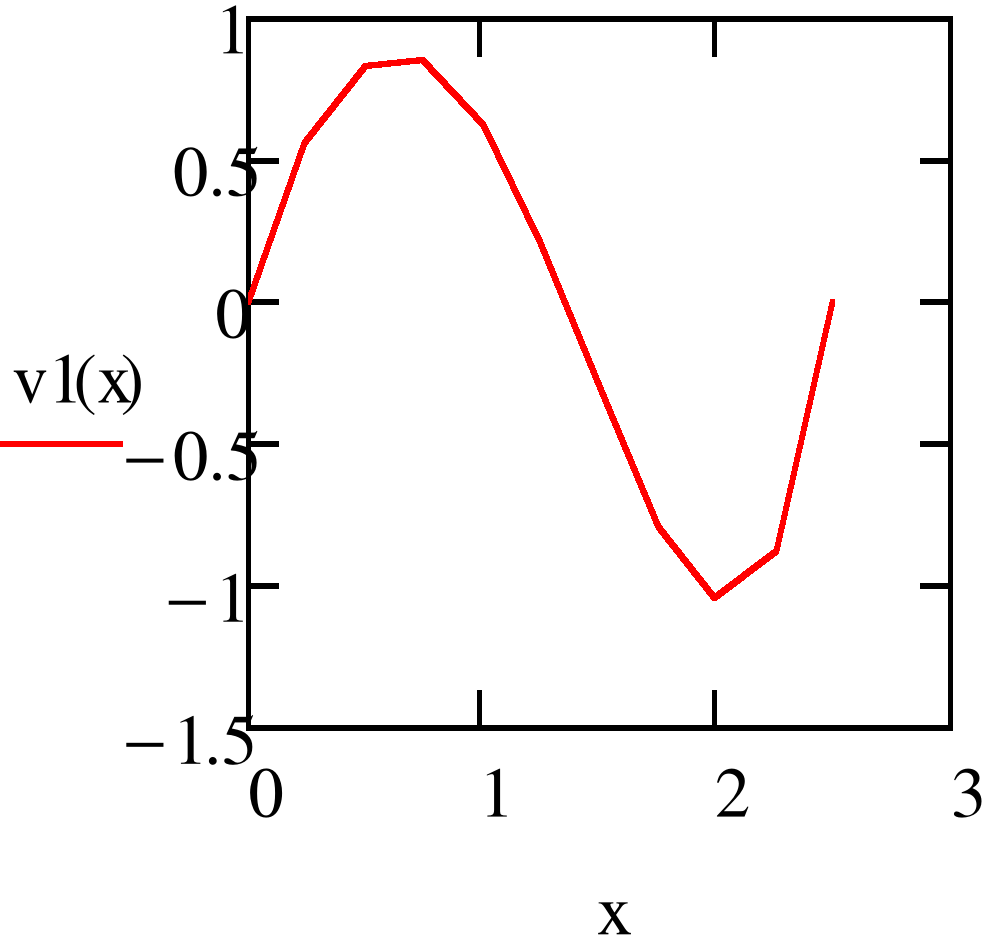
Рис. 4.4.Эпюра угла поворота оси балки
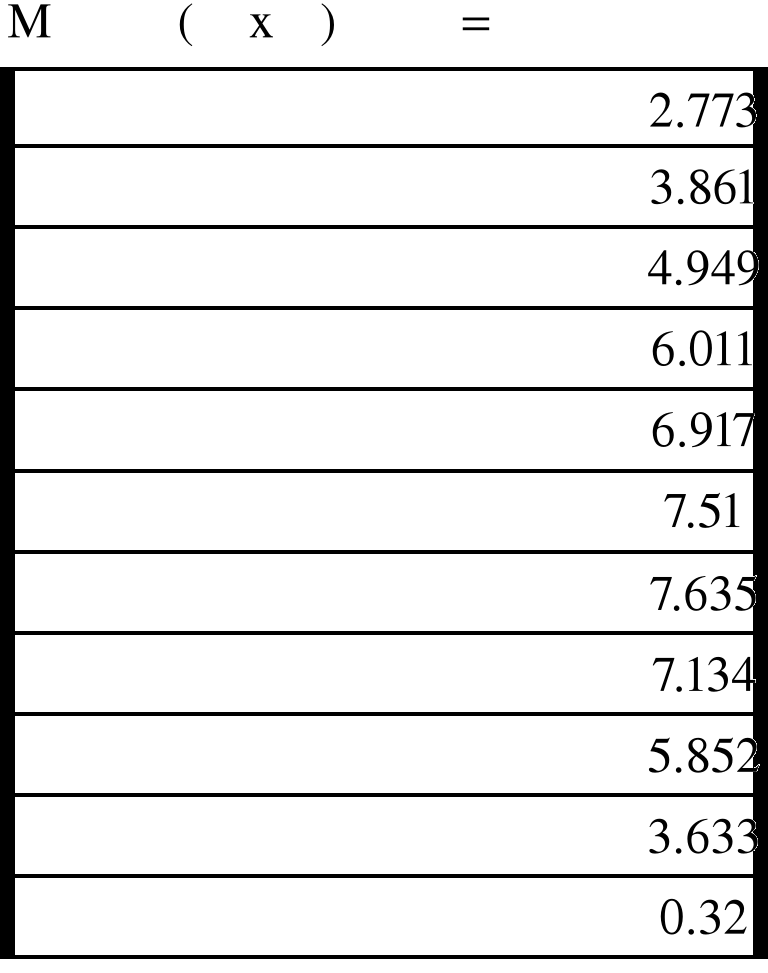
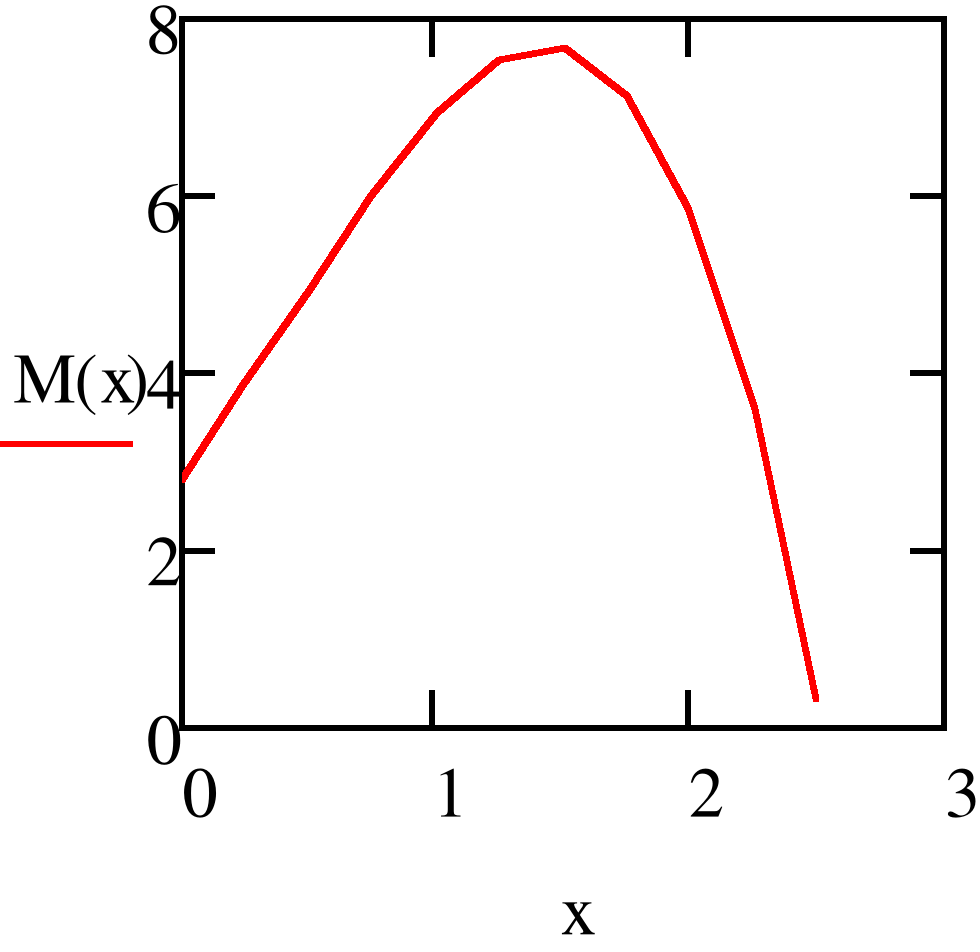
Рис. 4.4.Эпюра изгибающего момента балки
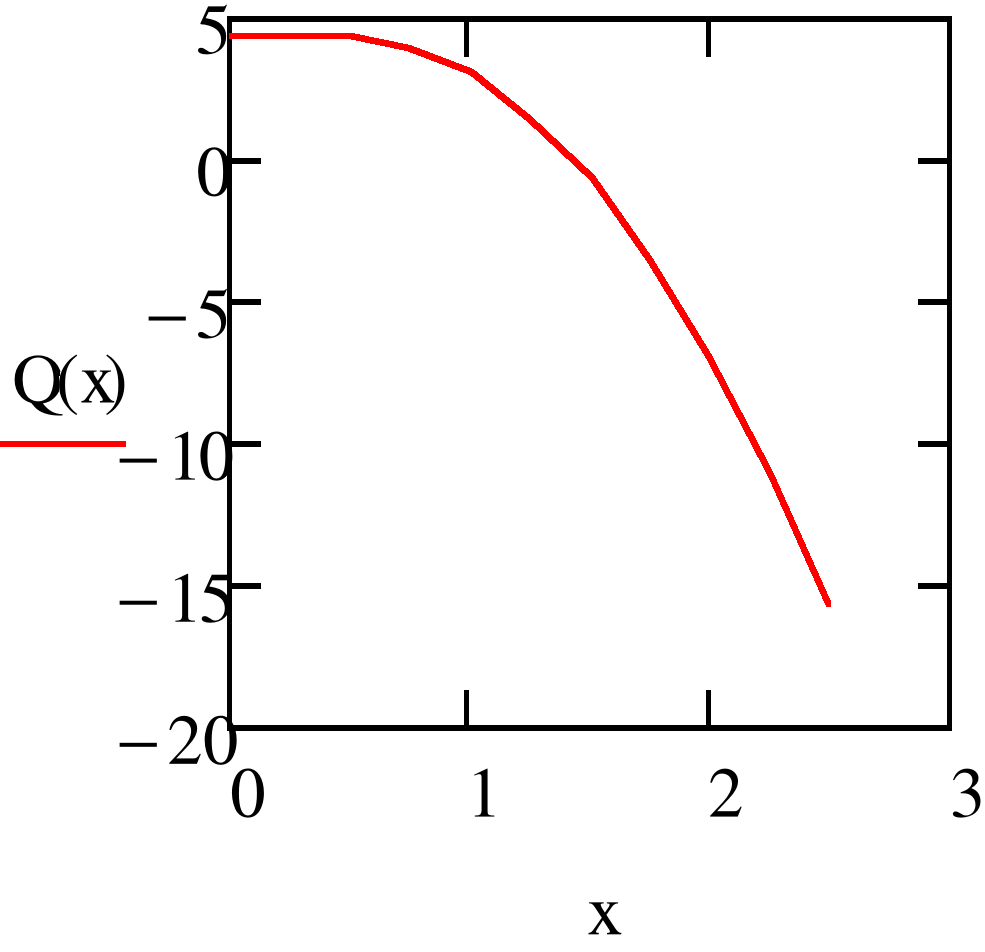
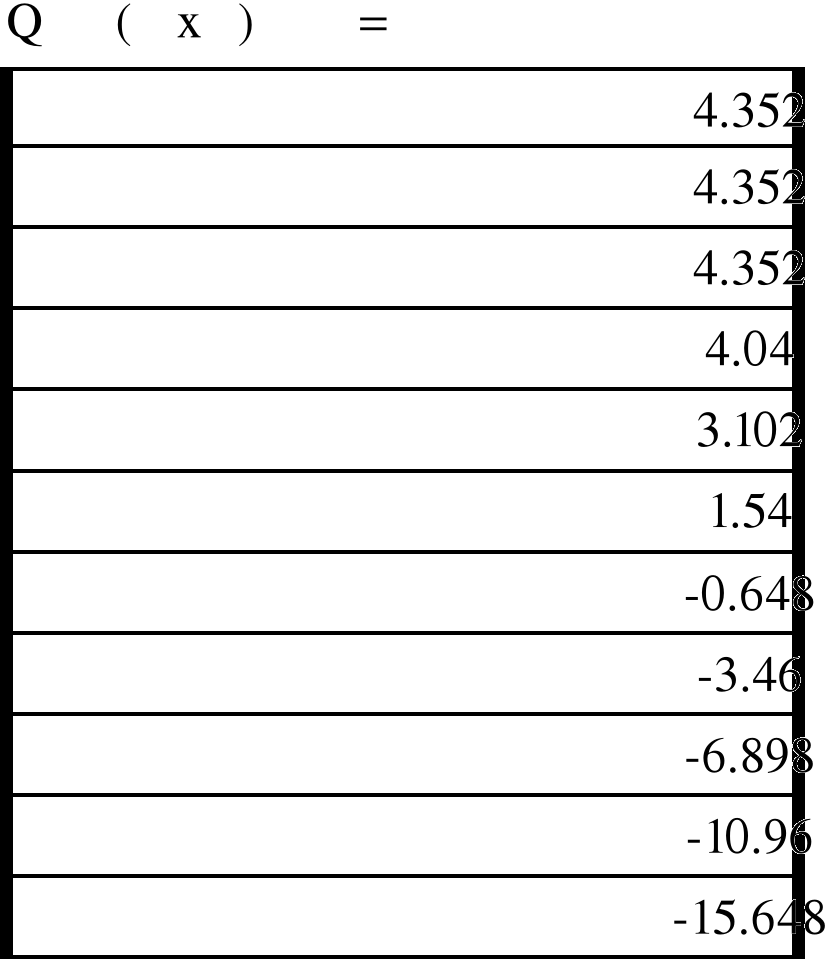
Рис. 4.5.Эпюра перерезывающей силы балки
5. РЕШЕНИЕ В СРЕДЕ ПРОГРАММИРОВАНИЯ VISUAL BASIC
Вычисления проводятся по полученным формулам (2.2), (2.3), (2.5), (2.7) с использованием одного из операторов цикла: For…Next, Do…Loop или While…Wend.
Задача сведена к просчету значений четырех функций при изменении аргумента на промежутке с некоторым шагом (задача табулирования функции).
Интерфейс приложения для вычисления прогиба, угла поворота, изгибающего момента и перерезывающей силы показан на рис.5.1. Для вывода результатов был применен объект ListBox.
Рис. 5.1. Интерфейс и результаты вычисления прогиба, угла поворота, изгибающего момента и перерезывающей силы
Программный код, написанный в среде программирования Visual Basic:
Рис. 5.2. Программный код в среде программирования Visual Basic
ВЫВОДЫ
В курсовой работе была решена задача по сопротивлению материалов – расчетбалки на изгиб методом начальных параметров - с применением ранее полученных знанийпо курсу информатики, а также с использованием методической литературы иконсультаций у преподавателя.
Курсовая работа была выполнена и оформлена с помощью программ: текстовыйредактор Microsoft Word, электронные таблицы Microsoft Excel, графический редакторPaint, автоматизированная система MathCad, среда программирования Visual Basic.
В данной курсовой работе расчет балки на изгиб, благодаря программам MicrosoftExcel и MathCad, был выполнен в несколько раз быстрее и нагляднее, по сравнению собычным расчетом, без использования компьютерной техники, что перспективно дляинженеров в настоящее время.
В результате проведенных расчетов были вычислены все характеристики
изогнутой балки: прогиб, угол поворота, изгибающий момент и перерезывающая сила.Полученные результаты и эпюры, выполненные разными программами, совпадают.
ИСПОЛЬЗОВАННЫЕ ИСТОЧНИКИ
- Беляев Н.М. Сопротивление материалов. – М.: Наука, 1976. – 608 с.
- Бидасюк Ю.М. Mathsoft® MathCAD11. Самоучитель. – М.: Издательский дом «Вильямс», 2004. – 224 с.
- Быкова О.Г. Информатика: Методические указания к курсовой работе для студентовспециальности 130504 / Санкт-Петербургский ГосударственныйГорный Институт им.Г.В.Плеханова, (технический университет). – СПб,2007, 44 с.
- Овчинникова Е.Н. Информатика. VISUAL BASIC: программирование циклических процессов. Графические возможности: Методические указания к лабораторным работам для студентов всех специальностей / Национальный минерально-сырьевой университет «Горный». – СПб, 2013, 40с.
- Онушника И.О., Талалай П.Г.Правила оформление курсовых и квалификационных работ: Методические указания.- СПб: Санкт-Петербургский государственный горный институт (технический университет), 2005.- 50 с.
- Рудикова Л.В. MicrosoftExcel для студента.- СПб: БХВ-Петербург, 2005.- 368 с.
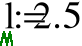
конец
Начало
q, l, с
X=0
x QUOTE 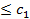
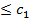
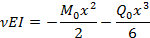
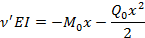
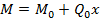
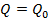
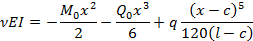
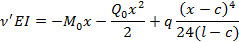
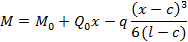
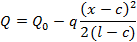
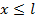
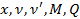
да
нет
да
нет
-
Расчет на прочность балки с жесткозаделанным левым и свободно опертым правым концом, нагруженной на части длины равномерной нагрузкой