Теория систем массового обслуживания
Министерство образования и науки РФ
Пермский национальный исследовательский политехнический университет
Кафедра автоматики и телемеханики
Теория систем массового обслуживания
ИНДИВИДУАЛЬНАЯ РАБОТА
Вариант № 3.3.5
|
Выполнил:
|
студент гр. АТз-12
Ситников Н.В.
Дата ________________
Подпись _____________
|
|
|
|
|
Проверил:
|
Зав. кафедрой АТ д.т.н., профессор Южаков А.А.
Дата ________________
Подпись _____________
|
Пермь 2015
Задание.
Разработать систему массового обслуживания (систему ПВО) с ожиданием, частичной взаимопомощью между каналами и ограниченным временем нахождения заявки в системе. Создать аналитическую и имитационную модель СМО и проверить их адекватность.
Системы ПВО, характеризуется следующими параметрами:
- Скорострельность каждой пусковой установки (выстрелов в минуту) - .
- Вероятность поражения цели одной ракетой - .
- Количество пусковых установок в одном канале обслуживания - .
- Число установок, обстреливающих один самолёт - .
- Зона обстрела - .
- Скорость налетающих самолетов, при условии, что они не обстреливаются
- Скорость налетающих самолетов, при условии, что они обстреливаются- .
- Среднее расстояние между самолетами - .
- Количество каналов обслуживания -
- Число мест в очереди m=1
Расчетные характеристики:
- среднее число занятых каналов;
- вероятность занятости канала обслуживания;
- среднее время очереди.
Содержание:
- Введение.
|
4
|
- Разработка имитационной модели.
|
6
|
- Математическое описание имитационной модели.
|
6
|
- Описание блок-схемы алгоритма.
|
7
|
- Анализ полученных результатов моделирования.
|
11
|
- Разработка аналитической модели.
|
12
|
- Математическое описание аналитической модели.
|
12
|
- Расчет параметров СМО.
|
14
|
- Анализ полученных результатов моделирования.
|
17
|
- Сопоставление полученных результатов для разработанных моделей.
|
18
|
- Выводы.
|
19
|
- Список литературы.
|
20
|
- Приложения
|
21
|
|
Приложение 1. Листинги программ моделирования.
|
21
|
|
Приложение 2. Таблицы результатов моделирования.
|
24
|
|
Приложение 3. Графики, полученные в результате моделирования.
|
26
|
Введение.
Рассматривается работа системы -канальной системы ПВО на вход которой поступают самолеты противника. Самолеты, пролетающие в пределах полосы налета, могут быть обстреляны любым из каналов данной системы ПВО.
Ширина полосы налета определяется возможностями обстрела всеми каналами любой цели в пределах полосы налета. Предполагается, что если самолет летит вне пределов полосы налета (слева или справа), тот эти самолеты не могут быть обстреляны ни одним из каналов данной системы ПВО.
Глубина зоны обстрела определяется рубежом перехвата и рубежом прекращения огня, которые являются одинаковыми для всех каналов
Необходимо отметить, что характеристики зоны обстрела и зависят также от скорости налетающих самолетов , высоты их полета и т.п.
Под каналом обслуживания будем понимать всю совокупность средств, обеспечивающих стрельбу по воздушной цели(например, радиолокационная станция наведения и нескольких пусковых установок).
Основные характеристики СМО:
- Работа каждого канала характеризуется временем, которое затрачивается на обслуживание одной заявки. В общем случае это время является случайным. Для простейших пуассоновских систем время обслуживания распределено по показательному закону с параметром . Это эквивалентно тому, что на выходе непрерывно занятого канала будет простейший поток обслуженных заявок с параметром . Как правило, все каналы имеют одинаковую интенсивность обслуживания . В этом случае нет необходимости различать каналы (первый, второй, и т. д.). Помимо этого, будем считать, что заявка может обслуживаться любым из n каналов, т. е. любой из n каналов «доступен» для заявки.
- Следующим важным параметром СМО является интенсивность (плотность) потока заявок . Здесь уместно напомнить, что заявки различаются лишь моментом поступления на обслуживание, а интенсивность потока заявок определяется через средний интерал между поступлениями двух заявок:
Каждый канал обслуживания обеспечивается пусковыми установками, а каждая пусковая установка производит в среднем выстрелов в минуту. Тогда эффективная скорострельность одного канала определится так:
,
где – вероятность поражения цели одной выпущенной по ней ракетой.
Среднее время пребывания цели в зоне обстрела:
,
где – скорость полета самолета, при условии, что она обстреливается.
Далее, в силу того, что мы рассматриваем только пуассоновские системы, будем считать, что время пребывания самолёта в зоне обстрела является показательным с параметром :
.
Тогда время занятости канала будет также подчинено показательному закону с параметром
.
Таким образом, поток освобождений канала ПВО, определяемый этим выражением, имеет интенсивность
.
Таким образом, видно, что поток освобождений канала слагается из двух потоков: потока поражающих выстрелов с параметром и потока уходов непоражённых самолётов из зоны обстрела с параметром . Другими словами канал освобождается либо по причине поражения самолёта, либо по причине выхода самолёта из зоны обстрела непоражённым. Если время передачи информации велико по сравнению со временем пребывания цели в зоне обстрела (типично для системы ПВО, у которой время мало), то
При анализе работы системы ПВО необходимо знать характеристики налета. Будем считать, что налетающие самолеты образуют пуассоновский поток с интенсивностью , который определяется так:
,
где – средний линейный интервал между самолетами.
В нашем случае время передачи информации мало и параметр освобождения канала определяется по формуле
2. Разработка имитационной модели.
- Математическое описание имитационной модели.
Имитационное моделирование основано на применении методов Монте-Карло (искусственной реализации вероятностных законов). С помощью генератора вырабатываются независимые реализации случайного процесса, интересующие нас характеристики находятся путём усреднения по множеству реализаций.
Приведём построение имитационной модели для заданной СМО.
Исходные данные для имитационной модели:
Дисциплина обслуживания - СМО с ожиданием, частичной взаимопомощью между каналами и ограниченным временем нахождения заявки в системе
- - число каналов обслуживания;
- - интенсивность простейшего входящего потока заявок;
- - интенсивность потока обслуживания заявок;
- - интенсивность простейшего потока освобождения канала;
Интенсивности поступления и обслуживания заявок распределены по пуассоновскому закону.
При разработке имитационной модели для реализации входного потока заявок и потока обслуживания из равномерной случайной величины, генерируемой ЭВМ, необходимо получить случайную величину, распределённую по пуассоновскому закону. Пусть - случайная величина, равномерно распределённая в интервале . Для пуассоновского распределения примем
Осуществив интегрирование, получим:
Решая это уравнение относительно , имеем:
.
Случайное число распределено равномерно в интервале , следовательно также случайная величина, принадлежащая интервалу . Поэтому и распределены одинаково. Отсюда имеем:
.
Определяемая этим соотношением случайная величина х имеет пуассоновский закон распределения. Таким образом, интервал времени между заявками определяется следующим образом:
,
где - случайная величина в диапазоне , генерируемая ЭВМ.
Требуемые характеристику СМО можно определить следующим образом:
,
- Вероятность полной загрузки:
,
- Среднее число занятых каналов:
,
Таким образом, используя имитационную модель можно получить требуемые параметры.
Имитационное моделирование включает следующие этапы:
1. Построение входного потока заявок. Время появления заявки определяется следующим образом:
,
где - модельное время.
2. Обслуживание заявок. Для каждой заявки, стоящей на обслуживании, проверяется, не истекло ли время её обслуживания. Если время истекло, то заявка считается обслуженной и занятые ей приборы освобождаются.
3. Генерация новой заявки. Генерируется время выполнения пришедшей заявки, т.к. оно распределено по пуассоновскому закону, то время выполнения:
,
где - время выполнения пришедшей заявки.
Далее заявка ставится на обслуживание, здесь возможны два варианта:
- в системе свободно приборов и заявка обслуживается одновременно приборами. При этом заявка обслуживается параллельно и интенсивность обслуживания заявки увеличивается в раз;
- число свободных приборов меньше . Заявка становится на обслуживание и обслуживается параллельно оставшимся числом приборов.
Блок-схема имитационного моделирования приведена на рис.1. Описание блок-схемы алгоритма приведено ниже.
2.2. Описание блок-схемы алгоритма.
Описание блок-схемы:
1) Установка начальных значений и обнуление счётчиков заявок, выполненных заявок, отказов.
Рассмотрим функционирование одного цикла моделирования:
2) Обнуление счетчиков занятых каналов.
3) Если текущее модельное время превышает время прихода следующей заявки, то генерируется новая заявка. Заявка генерируется в виде случайного промежутка времени, который распределён по пуассоновскому закону.
4) Проверка занятости каналов. Сохраняются номера свободных каналов, если они в данный момент есть, а также их количество.
5) Если количество свободных каналов больше, чем параметр взаимопомощи l, то заявка ставится на обслуживания. Постановка заявки на обслуживание происходит в виде генерации случайного промежутка времени распределённого по пуассоновскому закону.
6) Если количество свободных приборов меньше параметра взаимопомощи l, но больше нуля, то заявка ставится на обслуживание и обслуживается оставшимся числом свободных приборов. Постановка на обслуживание осуществляется как в предыдущем пункте
7) Если нет свободных приборов, то заявка становится в очередь (число мест в очереди ограничено)
8) Если нет мест в очереди, то заявка получает отказ в обслуживании и увеличивается на 1 счётчик отказов.
Далее идёт следующая итерация цикла.
9) Вычисление требуемых параметров СМО: -среднее число занятых каналов, - вероятность занятости канала, пз –вероятность полной занятости.
На основании изложенного алгоритма была разработана программа (Приложение 1). При имитационном моделировании для получения статистически достоверных результатов необходимо некоторое число реализаций. Чем больше , тем точнее оценки. В нашем случае количество реализаций можно найти по формуле:
,
где - дисперсия; - задаваемая точность; -уровень значимости.
При использовании данной формулы необходимо знать дисперсию , но она изначально неизвестна. Поэтому зададимся произвольным числом реализаций (10 реализаций), определим дисперсию, и найдём количество необходимых реализаций.
(В таблице 1 приложения 2 представлены полученные реализации).
Посчитаем дисперсию:
Зададимся точностью и уровнем значимости : для инженерных расчетов приемлемой считается погрешность не более 10%, поэтому точность можно взять,а уровень значимости . В этом случае число реализаций . Таким образом, имитационное моделирование было произведено с большей точностью.
2.3. Анализ полученных результатов моделирования.
В результате имитационного моделирования были получены следующие значения статических характеристик:
|
Число каналов обслуживания,
|
Искомый параметр
|
Результаты моделирования
|
|
|
|
1,012
|
|
|
|
0,576
|
|
|
|
0,323
|
|
|
|
1,731
|
|
|
|
0,482
|
|
|
|
0,288
|
|
|
|
3,584
|
|
|
|
0,427
|
|
|
|
0,234
|
Рассмотренный выше алгоритм построения имитационной модели реализован в программе imitaciya.pas. Текст программы в приложении 1, а результаты работы программы в виде таблицы — в приложении 2, графики представлены в приложении 3.
Проводя моделирование при увеличении числа обслуживающих приборов от 2 до 4, наблюдаем:
- увеличение среднего числа обслуживающих каналов;
- уменьшение среднего времени очереди;
- уменьшение вероятности полной занятости.
Существенным достоинством имитационной модели является возможность при многократном моделировании получить достаточно точные оценки рассчитываемых вероятностных показателей. Поэтому было произведено 10-ти кратное моделирование и усреднение полученных данных. Подробные результаты представлены в Приложении 2.
3. Разработка аналитической модели.
3.1. Математическое описание аналитической модели
При рассмотрении системы ПВО взаимопомощь между каналами состоит в том, что одну цель могут одновременно обстреливать каналов, при этом эффективная скорострельность увеличивается в раз.
Постановка задачи: На вход n – канальной СМО поступает простейший поток заявок с плотностью . Плотность простейшего потока обслуживания каждого канала . Если поступившая на обслуживание заявка застаёт все каналы свободными, то она принимается на обслуживание и обслуживается одновременно каналами (). При этом поток обслуживаний одной заявки будет иметь интенсивность . Если поступившая на обслуживание заявка застаёт в системе одну заявку, то при вновь прибывшая заявка будет принята к обслуживанию одновременно каналами с производительностью . Если поступившая на обслуживание заявка застаёт в системе i заявок (, при этом , то поступившая заявка будет обслуживаться каналами с общей производительностью . Если вновь поступившая заявка застаёт в системе заявок и при этом выполняются совместно два неравенства , то заявка будет принята на обслуживание. В этом случае часть заявок будет обслуживаться каналами, а одна заявка будет обслуживаться меньшим, чем числом каналов, но в обслуживании будут заняты все каналы. Если вновь поступившая заявка застанет в системе все каналы занятыми, то она получает отказ и не обслуживается.
Этой системе соответствует граф состояний:
За состояние принимается наличие в системе одной заявки.
Таким образом, возможны два варианта
1) , т. е. остаток от деления числа каналов обслуживания на число каналов, которые одновременно обслуживают одну заявку, равен нулю. В этом случае каждая заявка обслуживается каналами.
2) . Если в системе h заявок, то заявка обслуживается приборами, одна заявка приборами.
Так как система пуассоновского типа, то . Поэтому можно записать систему алгебраических уравнений в общем виде:
- вероятность того, что система находится в состоянии .
Последнее уравнение системы представляет собой условие нормировки, так как мы имеем дело с полной группой событий. Решив данную систему алгебраических уравнений можно найти вероятности нахождения системы в каждом из состояний.
Ниже представлен общий вид формул, по которым рассчитываются интересующие нас вероятностные характеристики
Вероятность занятости канала:
Для упрощения дальнейших выкладок введём обозначения:
, , ,
С учетом этих обозначений получим:
, где (0 < i < h)
,(h<j<n)
,где (0<r<m)
Вероятность занятости каналов:
Среднее число занятых каналов:
Вероятность полной загрузки:
и - табличные функции пуассоновского распределения
Определим значения интенсивности потока поступления заявок и потока освобождения каналов :
3.2. Расчёт параметров СМО.
Произведем расчет по графу состояний СМО.
- Запишем граф состояний и систему уравнений для двухканальной СМО ().
Система будет иметь 4 состояния:
- X0 – нет заявок на обслуживании;
- X1 – 1 заявка на обслуживании (обслуживается двумя каналами);
- X2 – 2 заявки на обслуживании (обслуживаются двумя каналами);
- Х3 – 2 заявки на обслуживании (обслуживаются двумя каналами), 3-я заявка в очередь;
Граф состояний имеет вид:
Этому графу соответствует система алгебраических уравнений, которую необходимо решить для получения интересующих параметров.
Определим искомые параметры:
Среднее число занятых каналов:
Среднее время очереди:
Вероятность полной загрузки:
- Запишем граф состояний и систему уравнений для трёхканальной СМО ().
В этом случае система будет иметь 5 состояния.
- X0 – нет заявок на обслуживании;
- X1 – 1 заявка на обслуживании (обслуживается двумя каналами);
- X2 – 2 заявки на обслуживании (одна обслуживается двумя каналами, другая - одним);
- X3 – 3 заявки в системе (каждая обслуживается одним прибором);
- X4 – 4 заявки в системе (3 заявки обслуживаются тремя каналами, четвертая в очередь);
Граф состояний имеет вид:
Этому графу соответствует система алгебраических уравнений, которую необходимо решить для получения интересующих параметров.
Определим искомые параметры:
Среднее число занятых каналов:
Среднее время очереди:
Вероятность полной загрузки:
- Запишем граф состояний и систему уравнений для четырёхканальной СМО ().
В этом случае система будет иметь 6 состояний.
- X0 – нет заявок на обслуживании;
- X1 – 1 заявка на обслуживании (обслуживается двумя каналами);
- X2 – 2 заявки на обслуживании (обе обслуживаются двумя каналами);
- X3 – 3 заявки на обслуживании (одна обслуживается двумя каналами, а на 2 оставшиеся приходится по одному каналу);
- X4 – 4 заявки в системе (каждая заявка обслуживается одним каналом);
- X5 – 5 заявок в системе (четыре обслуживаются четырьмя приборами, одна в очереди);
Этому графу соответствует система алгебраических уравнений, которую необходимо решить для получения интересующих параметров.
Определим искомые параметры:
Среднее число занятых каналов:
Среднее время очереди:
Вероятность полной загрузки:
|
Число каналов обслуживания,
|
Искомый параметр
|
Аналитическая модель
|
|
|
|
1,006
|
|
|
|
0,563
|
|
|
|
0,325
|
|
|
|
1,728
|
|
|
|
0,483
|
|
|
|
0,289
|
|
|
|
2,679
|
|
|
|
0,452
|
|
|
|
0,223
|
3.3. Анализ полученных результатов моделирования.
В результате аналитического моделирования получены интересующие нас вероятностные характеристики системы. При аналитическом моделировании характеристики были посчитаны по заранее известным формулам [3]. Результаты аналитического моделирования представлены также в Приложении 2. А требуемые графики в Приложении 3. Также была исследована зависимость вероятностных характеристик системы от числа обслуживающих приборов. При увеличении числа обслуживающих приборов от 2 до 4 были выявлены следующие закономерности: вероятность обслуживания возрастает, вероятность занятости канала уменьшается, среднее число занятых каналов увеличивается. Эти закономерности в виде графиков представлены в Приложении 3.
4. Сопоставление полученных результатов для разработанных моделей.
Чтобы убедиться в адекватности применяемых моделей СМО, воспользуемся статистическим критерием , который служит для проверки однородности двух независимых выборок. Если выборки однородны, то считают, что они извлечены из одной генеральной совокупности и, следовательно, имеют одинаковые, причем неизвестные, непрерывные функции распределения и .
Таким образом, нулевая гипотеза состоит в том, что при всех значениях аргумента функции распределения равны между собой:
Для того, чтобы при заданном уровне значимости и количестве степеней свободы проверить нулевую гипотезу : об однородности двух независимых выборок объемов и ():
,
и сравнить полученное значение с табличным для данных и .
Если , гипотезу об адекватности отвергают.
Если , гипотеза об адекватности принимается.
Зададимся уровнем значимости (число степеней свободы ), при объеме выборки .
Значение для данных параметров равно 0.102.
Пусть в качестве вероятность отказа в обслуживании для аналитической модели, а – для имитационной модели.
Результаты расчетов сведём в таблицу.
|
|
|
|
|
0,266
|
0,264
|
|
|
0,394
|
0,382
|
|
|
0,421
|
0,413
|
|
|
0,441
|
0,427
|
|
|
|
|
|
Из таблицы получили , поэтому принимаем нулевую гипотезу об однородности выборок.
Таким образом, результаты сравнения показывают адекватность моделей.
5. Выводы.
В процессе выполнения данной индивидуальной работы мы познакомились с системами массового обслуживания на примере системы ПВО с конечной очередью и частичной взаимопомощью. Данная система ПВО была рассмотрена как система массового обслуживания с конечной очередью и частичной взаимопомощью между каналами обслуживания.
Для заданной системы были построены две модели: аналитическая модель и имитационная модель. Обе системы рассматриваются при следующих упрощениях: рассматривается простейший пуассоновский поток входящих заявок, простейший пуассоновский поток обслуживания, а также система работает в стационарном режиме. В аналитической модели можно путем решения алгебраической системы уравнений можно определить вероятностные характеристики системы – вероятность обслуживания, вероятность занятости канала, среднее время простоя канала и др.
Имитационная модель строилась с учетом всех особенностей функционирования реальной системы и поэтому она достаточно точно описывает все вероятностные процессы. В основу имитационной модели положено рассмотрение работы системы на некотором отрезке времени. В результате этого можно определить вероятностные характеристики системы. Листинг программы имитационного моделирования imitaciya.pas приведён в Приложении 1.
На этапе сравнения двух построенных моделей с помощью критерия были сделаны следующие вывод - с точки зрения вычисления такой характеристики системы как вероятность отказа модели (аналитическая и имитационная) адекватны.
Также была выявлена зависимость вероятностных характеристик системы от числа обслуживающих приборов, были получены следующие закономерности. Проводя моделирование при увеличении числа обслуживающих приборов от 2 до 4, наблюдаем:
- увеличение среднего числа обслуживающих каналов;
- уменьшение среднего времени очереди;
- уменьшение вероятности полной занятости.
Соответствующие зависимости в виде графиков представлены в Приложении 3.
6. Список используемой литературы.
- ГОСТ 19.105-78. ЕСПД. «Общие требования к программным документам».
- Овчаров Л. А., «Прикладные задачи теории массового обслуживания», Москва, Машиностроение, 1969.
- Гмурман В. Е., «Теория вероятностей и математическая статистика». М: Высшая школа, 1977.
7. Приложения
Приложение 1. Листинг программ моделирования.
{программа имитационного моделирования}
Program imitaciya;
const
lambda=3.57; {Интенсивность простейшего входящего потока}
muz=1.147; {Интенсивность простейшего потока освобождения канала}
mu=0.835; {Интенсивность простейшего потока обслуживания}
time_t=1000000; {Время моделирования}
n_kanalov=4; {Число каналов обслуживания}
l=2; {Параметр взаимопомощи}
var
n_svob,p:integer; {кол-во свободных в данный момент приборов}
vypolneno:real; {Количество выполненных заявок}
kolvo,otkaz:longint; {Кол-во заявок, кол-во отказов}
i,ok:integer;
t:longint; {Текущее время при моделировании}
t_z0,t_z,t_obs:real; {Интервалы обслуживания и занятости заявки}
n:array[1..n_kanalov] of real;{Массив, в котором хранится время занятости текущего канала}
t_zan:array[1..n_kanalov] of real;{Массив, в котором хранится общее время занятости каждого канала во время моделирования}
n_vyp:array[1..n_kanalov] of real;{Массив, в котором хранится кол-во заявок, выполненных каждым каналом}
n_l_z:array[1..n_kanalov] of integer;
Pobs,Pzk:real; {Вероятность обслуживания и вероятность занятости канала}
tpk:real; {Среднее время простоя канала}
n_zero:array[1..l] of integer; {Номера свободных в данный момент каналов обслуживания}
begin
randomize;
t_z0:=0;
kolvo:=0;
otkaz:=0;
vypolneno:=0;
for i:=0 to n_kanalov do {Начальное обнуление параметров}
begin
n_vyp[i]:=0;
t_zan[i]:=0;
end;
for t:=0 to time_t do {Основной цикл моделирования}
begin
for i:=1 to n_kanalov do {Цикл проверки окончания обслуживания заявки}
begin
if ((t>n[i])AND(n[i]<>0)) then {Если текущее время больше, чем время окончания}
begin {обслуживания заявки, то канал вобождается и увеличивается счётчик выполненных заявок}
n[i]:=0;
vypolneno:=vypolneno+1/n_l_z[i];
n_l_z[i]:=0;
end;
end;
if (t>=t_z0) then {Генерации прихода новой заявки}
begin
t_z:=-100/lambda*ln((random(1000)+1)/1000);{генерация случайного интервала между заявками}
t_z0:=t_z0+t_z;
inc(kolvo); {Счётчик числа пришедших заявок увеличивается на единицу }
n_svob:=0;
for i:=1 to l do n_zero[i]:=0; {Обнуляется массив номеров свободных каналов}
p:=1;
for i:=1 to n_kanalov do {Цикл поиска свободных каналов}
begin
if (n[i]=0) then
begin
inc(n_svob);
n_zero[p]:=i;
inc(p);
end;
end;
if (n_svob>=l) then begin {если число свободных каналов больше, чем l, то поступившая заявка обслуживается l приборами}
t_obs:=-100/(l*muz)*ln((random(1000)+1)/1000); {Генерация времени обслуживания заявки}
for i:=1 to l do {Распределяем обслуживание заявки по l каналам}
begin
n[n_zero[i]]:=t+t_obs; {Записываем время окончания обслуживания заявки}
n_l_z[n_zero[i]]:=l;
t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;{Общее время занятости i-го канала}
n_vyp[n_zero[i]]:=n_vyp[n_zero[i]]+1; {Число заявок, выполненных i-тым каналом}
ok:=1; {Заявка поставлена на обслужитвание}
end;
end
else
if (n_svob>0)AND(n_svob<l) then begin {если число свободных каналов меньше, чем l, то заявка обслуживается меньшим числом}
t_obs:=-100/(n_svob*muz)*ln((random(1000)+1)/1000); {Генерация времени обслуживания заявки}
for i:=1 to n_svob do {Распределяем обслуживание заявки по оставшимся свободным каналам}
begin
n[n_zero[i]]:=t+t_obs; {Записываем время окончания обслуживания заявки}
n_l_z[n_zero[i]]:=n_svob;
t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;{Общее время занятости i-го канала}
n_vyp[n_zero[i]]:=n_vyp[n_zero[i]]+1; {Число заявок, выполненных i-тым каналом}
ok:=1; {Заявка поставлена на обслужитвание}
end;
end
else ok:=0; {иначе заявка не поставлена на обслуживание}
if (ok<>1) then inc(otkaz); {Если заявка не поставлена на обслуживание, то увеличивается счётчик отказов на единицу}
end;
end; {Окончание основного цикла моделирования}
{Вычисление интересующих параметров по результатам моделирования}
pzk:=0;
for i:=1 to n_kanalov do pzk:=pzk+t_zan[i]/time_t;
pzk:=pzk/n_kanalov;
tpk:=0;
for i:=1 to n_kanalov do if (n_vyp[i]<>0) then tpk:=tpk+(time_t-t_zan[i])/n_vyp[i];
tpk:=tpk/n_kanalov;
Pobs:=mu/muz*vypolneno/kolvo;
writeln('Число заявок ',kolvo);
writeln('Выполнено ',vypolneno:5:0);
writeln('Время очереди ',toch/100:5:3); {Вывод результатов моделирования}
writeln('Вероятность полной занятости ',Ppz:5:3);
writeln('Среднее число занятых каналов ',t:5:3);
{readln; }
end.
Приложение 2. Таблицы результатов моделирования.
Таблица 1. Результаты имитационного моделирования:
|
Число каналов обслуживания,
|
Номер реализации
|
|
|
|
|
|
1
|
1,001
|
0,581
|
0,328
|
|
|
2
|
1,022
|
0,574
|
0,323
|
|
|
3
|
1,021
|
0,592
|
0,320
|
|
|
4
|
1,023
|
0,571
|
0,328
|
|
|
5
|
1,003
|
0,569
|
0,324
|
|
|
6
|
1,006
|
0,557
|
0,322
|
|
|
7
|
1,004
|
0,595
|
0,316
|
|
|
8
|
1,011
|
0,562
|
0,332
|
|
|
9
|
1,021
|
0,581
|
0,329
|
|
|
10
|
1,009
|
0,579
|
0,312
|
|
|
среднее
|
1,012
|
0,576
|
0,323
|
|
|
1
|
1,711
|
0,474
|
0,301
|
|
|
2
|
1,722
|
0,494
|
0,283
|
|
|
3
|
1,743
|
0,483
|
0,271
|
|
|
4
|
1,721
|
0,492
|
0,267
|
|
|
5
|
1,749
|
0,489
|
0,293
|
|
|
6
|
1,764
|
0,459
|
0,299
|
|
|
7
|
1,721
|
0,478
|
0,28
|
|
|
8
|
1,723
|
0,481
|
0,295
|
|
|
9
|
1,721
|
0,485
|
0,298
|
|
|
10
|
1,736
|
0,495
|
0,288
|
|
|
среднее
|
1,731
|
0,482
|
0,288
|
|
|
1
|
2,590
|
0,433
|
0,265
|
|
|
2
|
2,609
|
0,441
|
0,214
|
|
|
3
|
2,596
|
0,423
|
0,223
|
|
|
4
|
2,609
|
0,435
|
0,239
|
|
|
5
|
2,520
|
0,422
|
0,211
|
|
|
6
|
2,607
|
0,421
|
0,232
|
|
|
7
|
2,616
|
0,436
|
0,228
|
|
|
8
|
2,614
|
0,427
|
0,225
|
|
|
9
|
2,521
|
0,417
|
0,238
|
|
|
10
|
2,562
|
0,412
|
0,263
|
|
|
среднее
|
2,584
|
0,427
|
0,234
|
|
|
|
Таблица 2. Сравнение результатов имитационного и аналитического моделирования:
|
Число каналов обслуживания,
|
Искомый параметр
|
Аналитическая модель
|
Имитационная модель
|
|
|
|
1,006
|
1,012
|
|
|
|
0,573
|
0,576
|
|
|
|
0,325
|
0,323
|
|
|
|
1,728
|
1,731
|
|
|
|
0,483
|
0,482
|
|
|
|
0,289
|
0,288
|
|
|
|
2,679
|
2,584
|
|
|
|
0,452
|
0,427
|
|
|
|
0,223
|
0,234
|
|
|
Приложение 3. Графики, полученные в результате моделирования.
График 1. Зависимость среднего числа занятых каналов от числа приборов для аналитической и имитационной моделей.
График 2. Зависимость среднего времени очереди от числа каналов для аналитической и имитационной моделей
График 3. Зависимость вероятности полной загруженности системы от числа каналов для аналитической и имитационной моделей.
Зона обстрела а
Рубеж перехвата
Полоса
налета b
Рубеж прекращения огня
1
2
:
.
n
Каналы ПВО
EMBED Equation.3 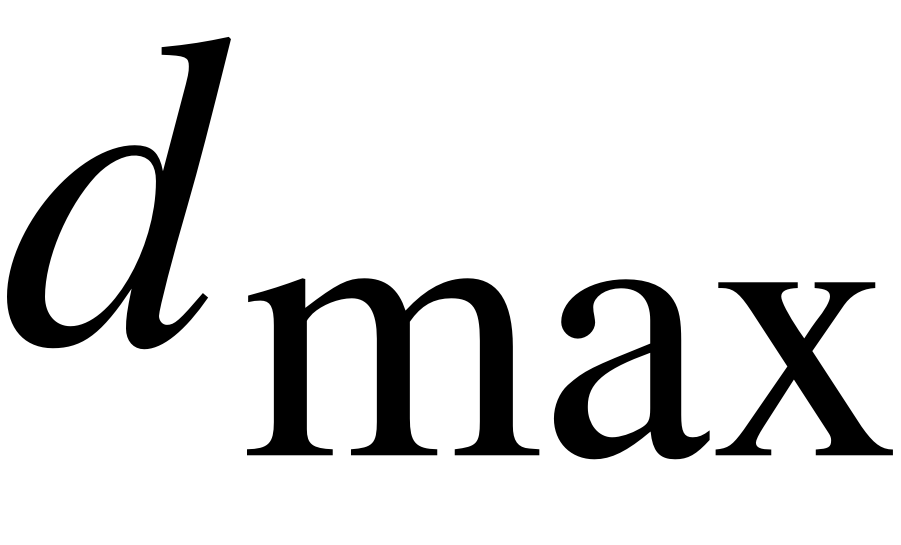
EMBED Equation.3 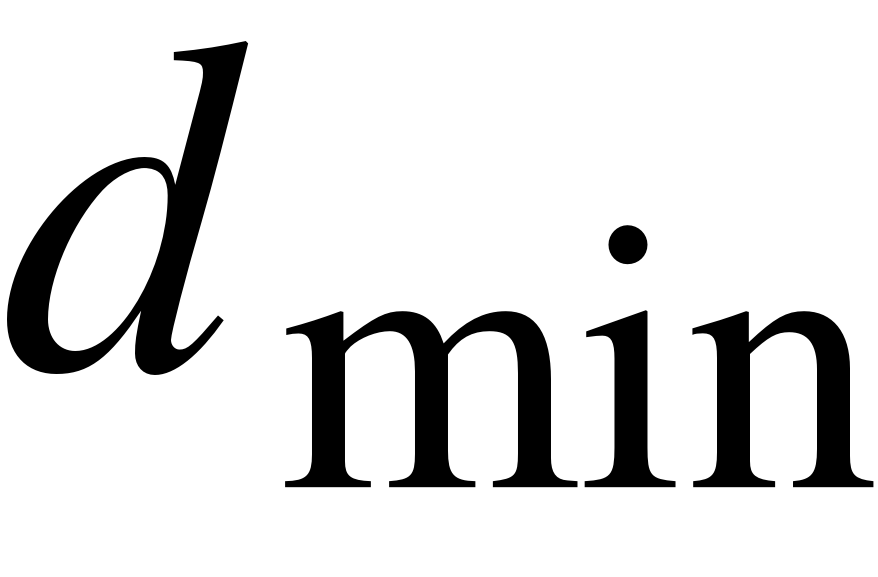
X0
X1
Xi
Xi+1
Xh-1
EMBED Equation.3 
EMBED Equation.3 
EMBED Equation.3 
EMBED Equation.3 
EMBED Equation.3 
EMBED Equation.3 
EMBED Equation.3 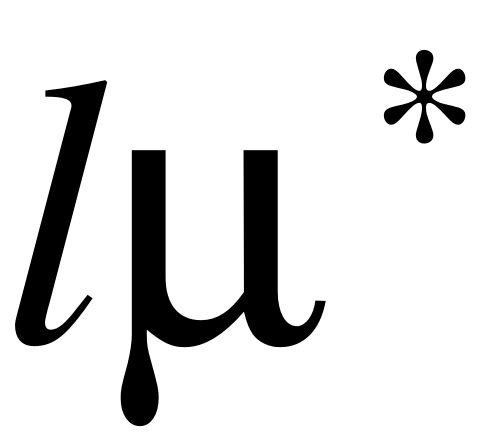
EMBED Equation.3 
EMBED Equation.3 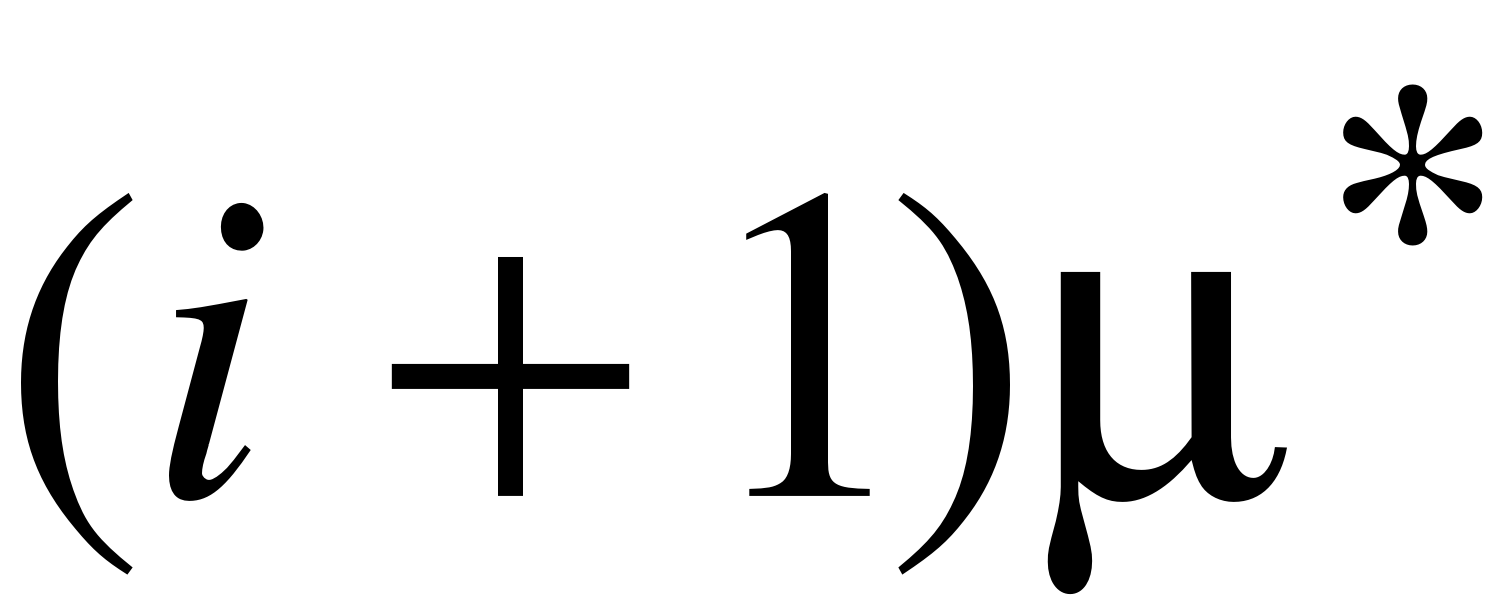
…
EMBED Equation.3 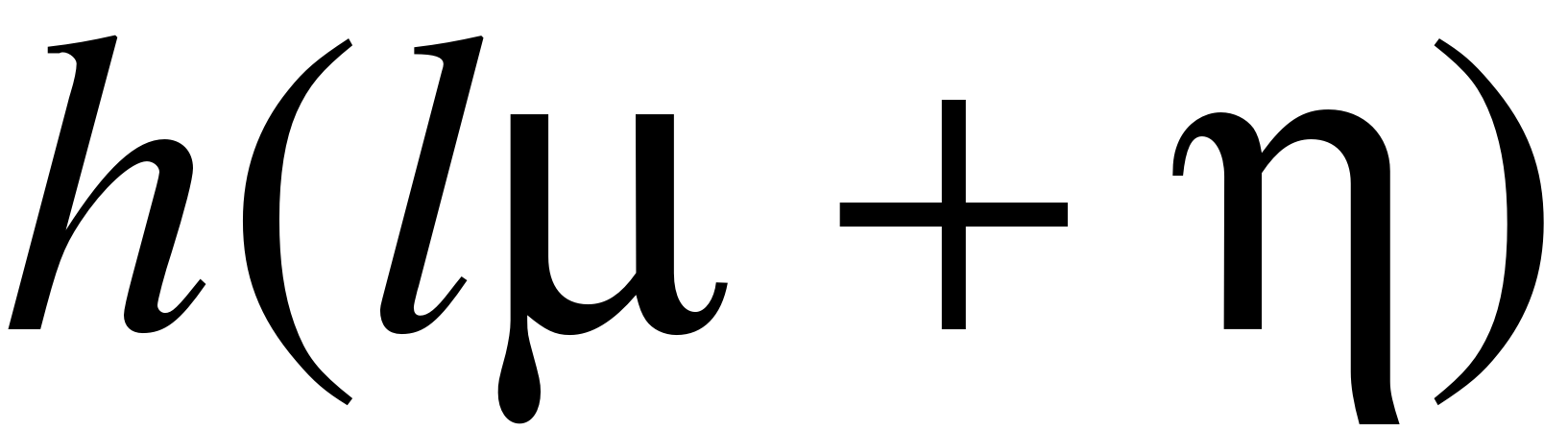
EMBED Equation.3 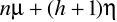
EMBED Equation.3 
EMBED Equation.3 
n(+)
n(*+m)
Xh
…
EMBED Equation.3 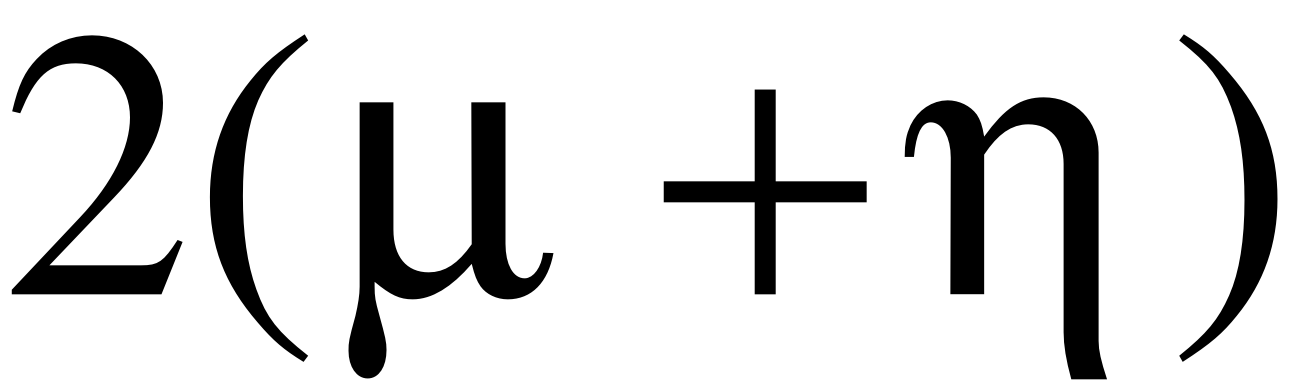
EMBED Equation.3 
EMBED Equation.3 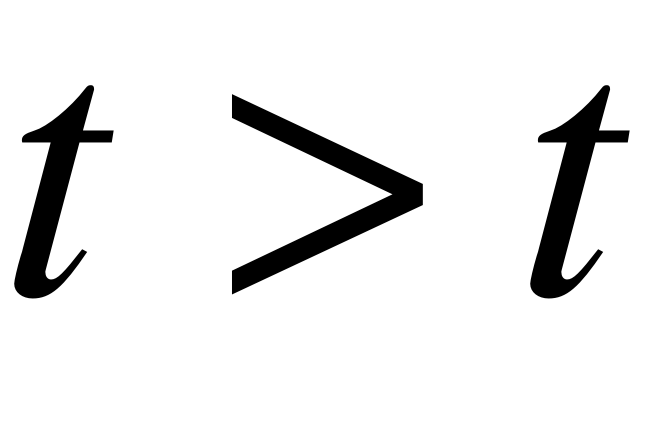
3
да (i-тый прибор свободен)
EMBED Equation.3 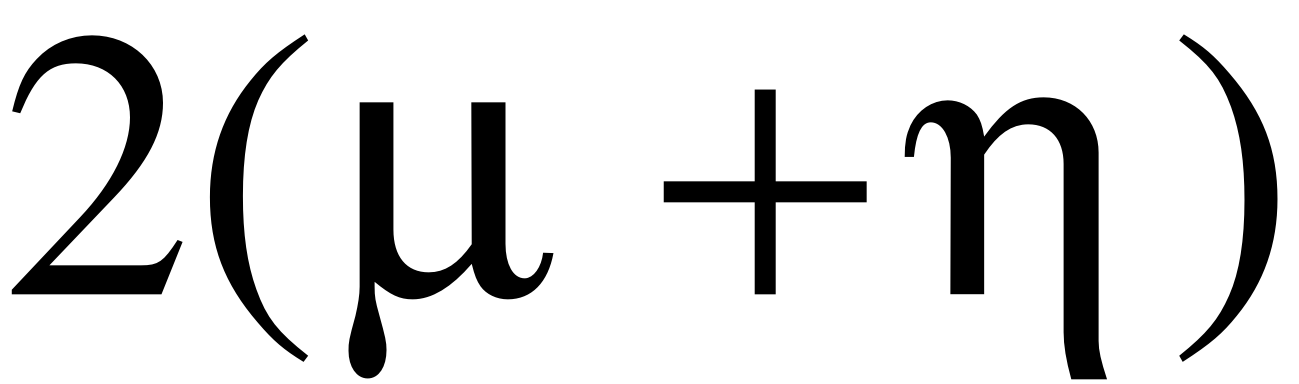
EMBED Equation.3 
EMBED Equation.3 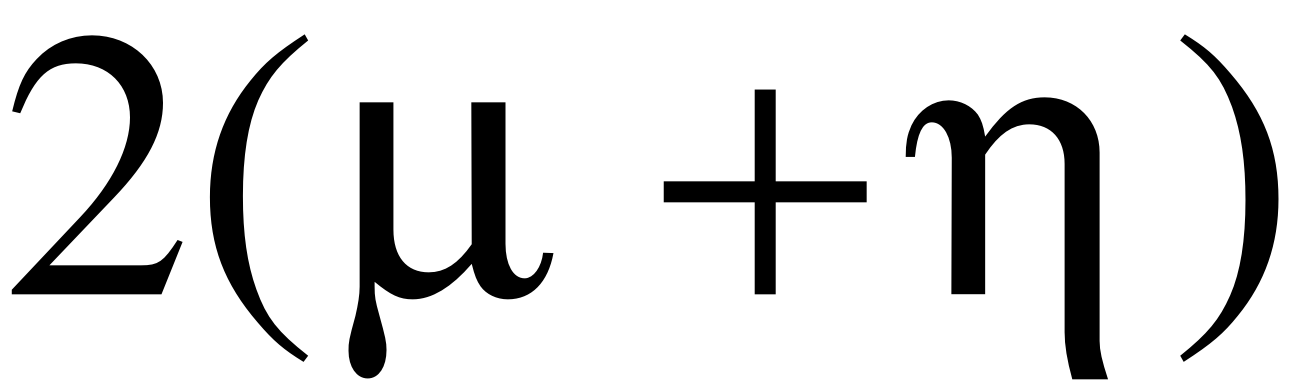
EMBED Equation.3 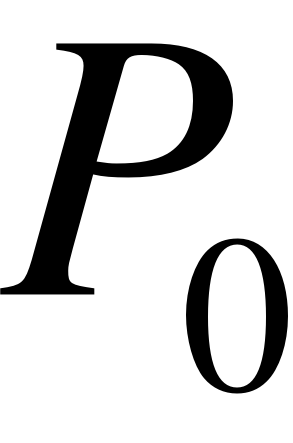
EMBED Equation.3 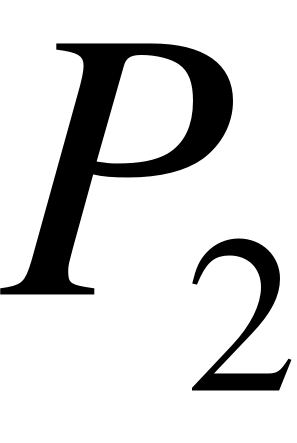
B
сли i-тый канал свободен, то записываем номер этого канала и увеличиваем счётчик свободных каналов на 1
EMBED Equation.3 
EMBED Equation.3 
да
да
А
inc(n_svob);
n_zero[n_svob]:=i;
EMBED Equation.3 
EMBED Equation.3 
нет
нет
EMBED Equation.3 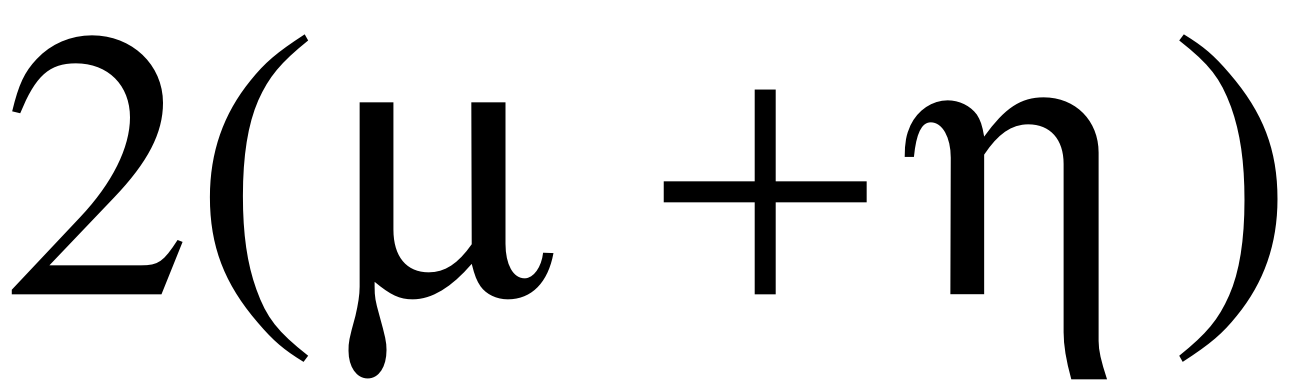
X2
n[i]=0
X2
X1
X0
For i:=1 to n
2
For t:=0 to t_time
1
EMBED Equation.3 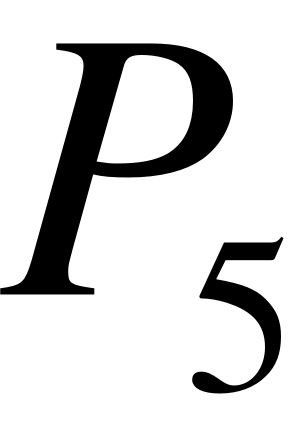
EMBED Equation.3 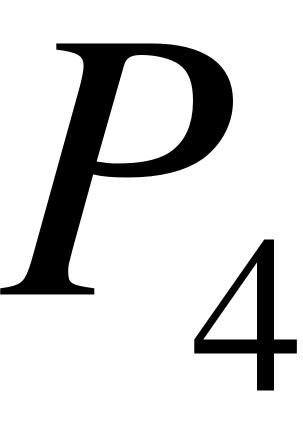
EMBED Equation.3 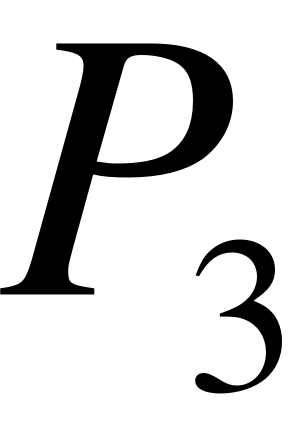
EMBED Equation.3 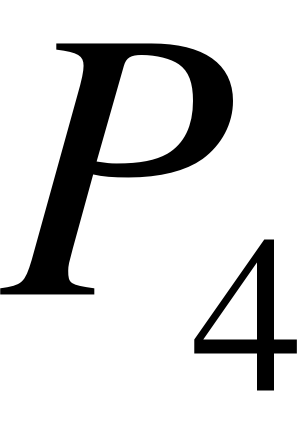
Генерация момента поступления следующей заявки и увеличение счётчика пришедших заявок
нет
For i:=1 to n_kanalov 3
EMBED Equation.3 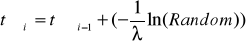 inc(kolvo);
inc(kolvo);
EMBED Equation.3 
EMBED Equation.3 
2
N[i]:=0;
vypolneno:= vypolneno+1/n_l_z[i]);
Свобождается i – тый канал, увеличивается счётчик выполненных заявок
EMBED Equation.3 
Обнуление счётчиков
EMBED Equation.3  - интенсивность поступления заявок;
- интенсивность поступления заявок;
EMBED Equation.3 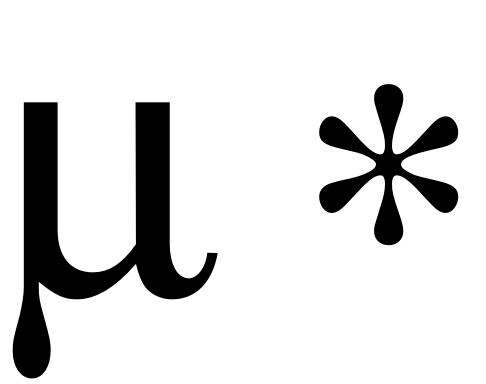 -интенсивность потока освобождения каналов;
-интенсивность потока освобождения каналов;
EMBED Equation.3 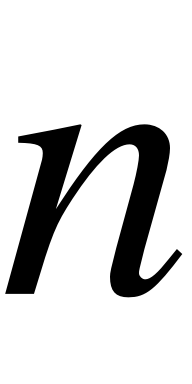 - число каналов обслуживания;
- число каналов обслуживания;
EMBED Equation.3 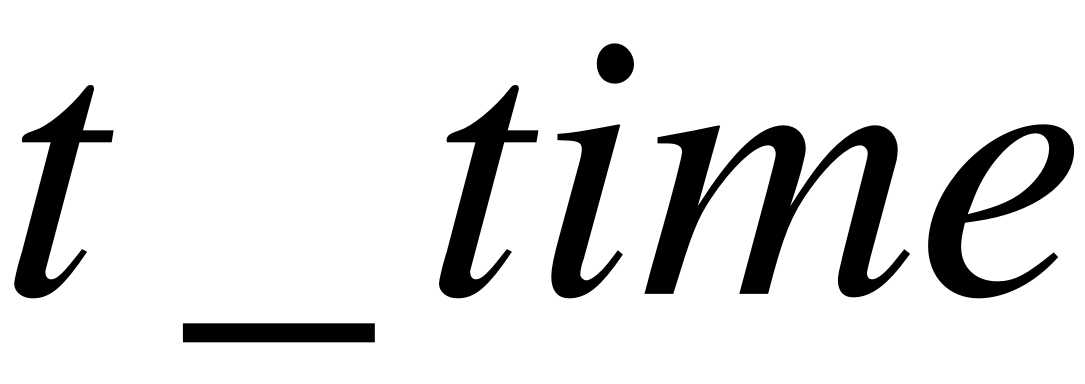 - время моделирования;
- время моделирования;
l – параметр взаимопомощи
Ввод исходных данных: EMBED Equation.3 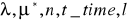
начало
EMBED Equation.3 
нет
нет
да (число свободных каналов больше l)
If n_svob>l
EMBED Equation.3 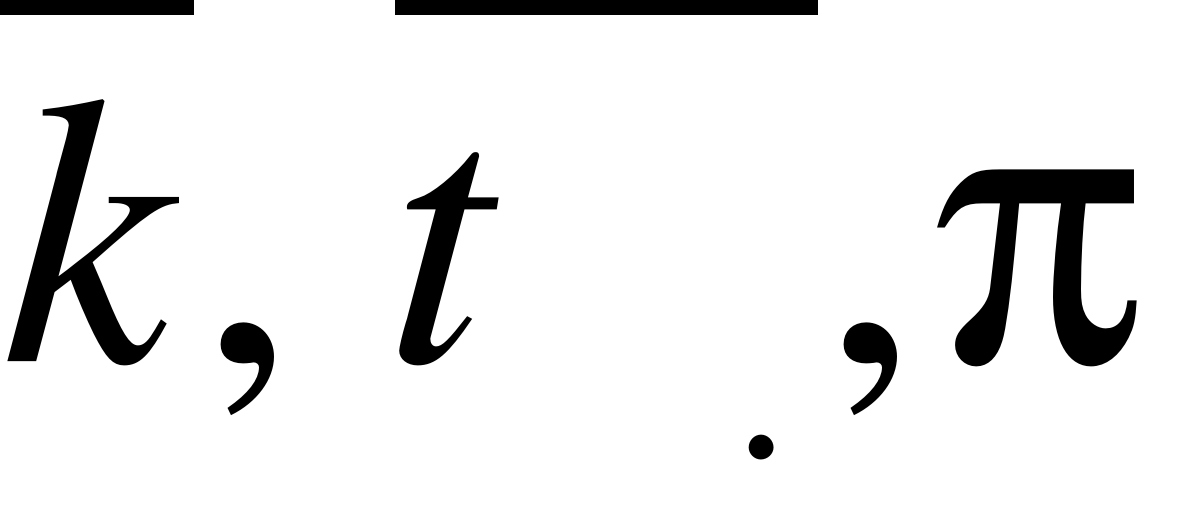
Обнуление счётчиков свободных каналов
А
Заявка ставится на обслуживание и обслуживается l приборами параллельно
t_obs:=100/(l*muz)*ln((random(1000)+1)/1000); for i:=1 to l do begin n[n_zero[i]]:=t+t_obs; n_l_z[n_zero[i]]:=l; t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;
ok:=1;
да (число свободных каналов больше 0 и меньше l)
If (n_svob>0)AND(n_svob<l)
t_obs:=100/(n_svob*muz)*ln((random(1000)+1)/1000); for i:=1 to l do begin n[n_zero[i]]:=t+t_obs; n_l_z[n_zero[i]]:=l; t_zan[n_zero[i]]:=t_zan[n_zero[i]]+t_obs;
ok:=1;
Заявка ставится на обслуживание и обслуживается оставшимися свободными приборами параллельно
нет
да
Заявка не встала на обслуживание, увеличивается счётчик отказов
Inc(otkaz);
Ok<>0
конец
1
B
Вывод результатов
ok=0
EMBED Equation.3 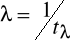
…
Xi-1
Xh+1
n(*+)
EMBED Equation.3 
Xn-1
Xn
Xn+1
Xn+m-1
Xn+m
X1
X0
EMBED Equation.3 
EMBED Equation.3 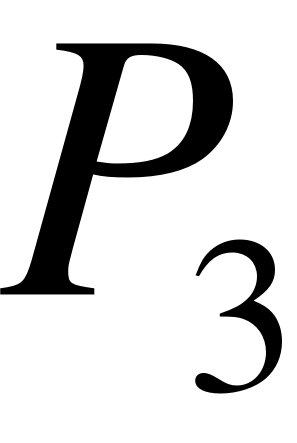
X3
EMBED Equation.3 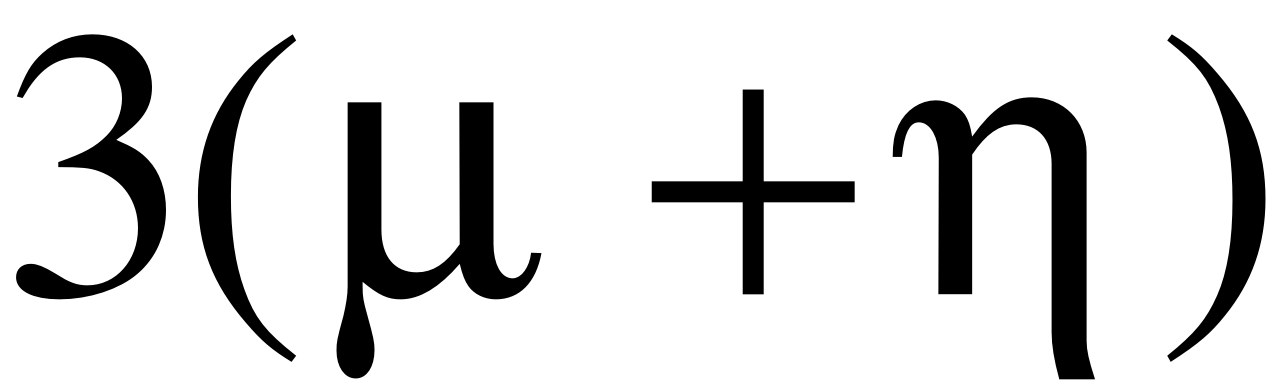
EMBED Equation.3 
X3
X4
EMBED Equation.3 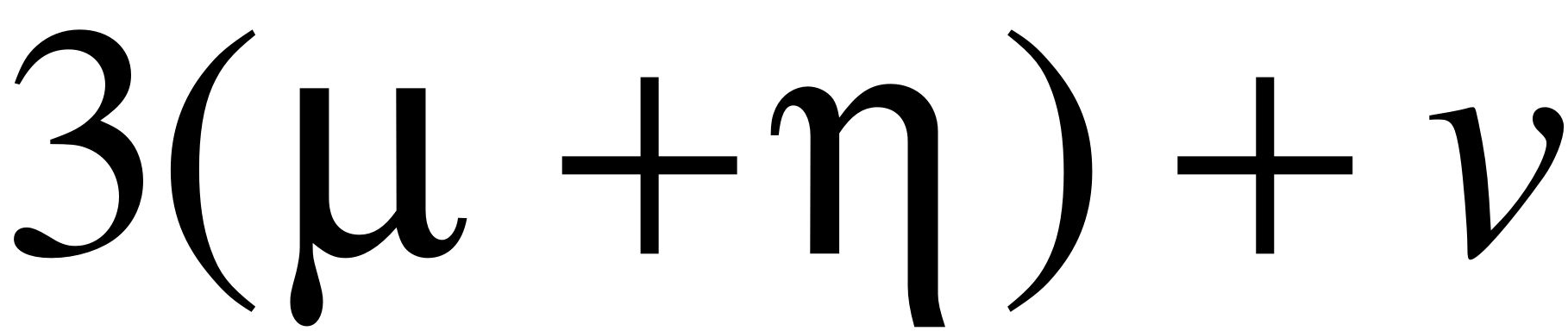
EMBED Equation.3 
EMBED Equation.3 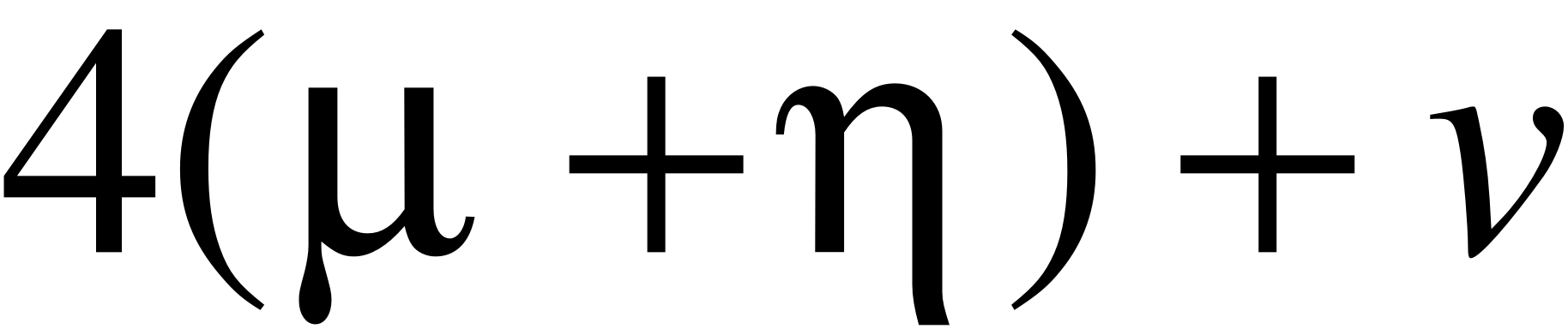
X5
EMBED Equation.3 
EMBED Equation.3 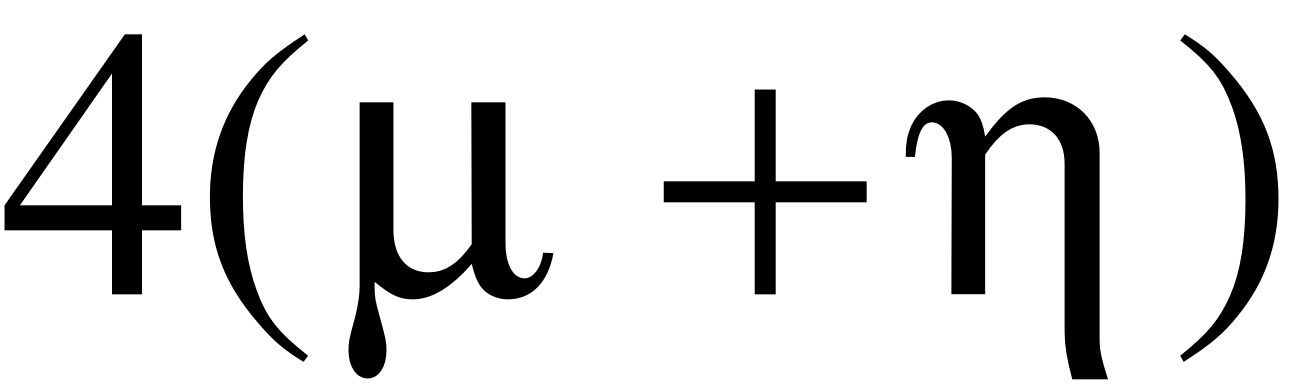
X4
EMBED Equation.3 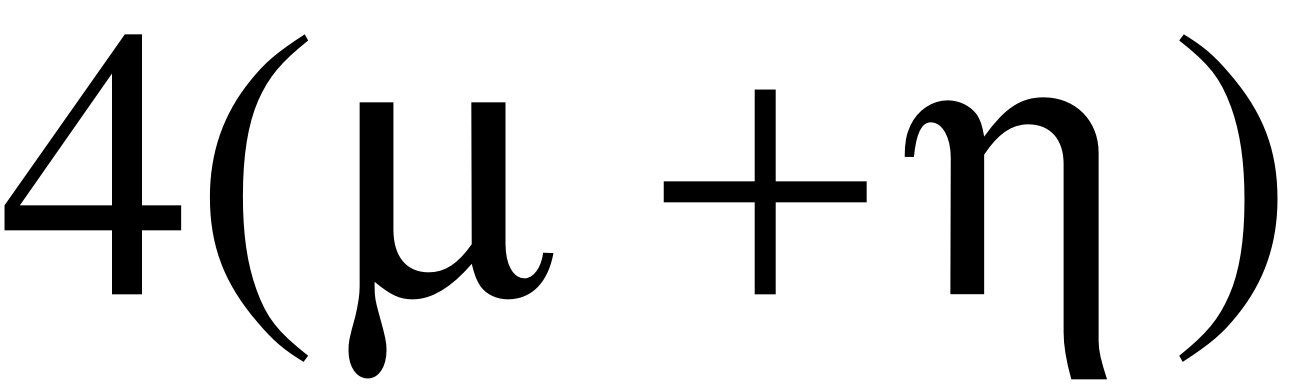
EMBED Equation.3 
X3
EMBED Equation.3 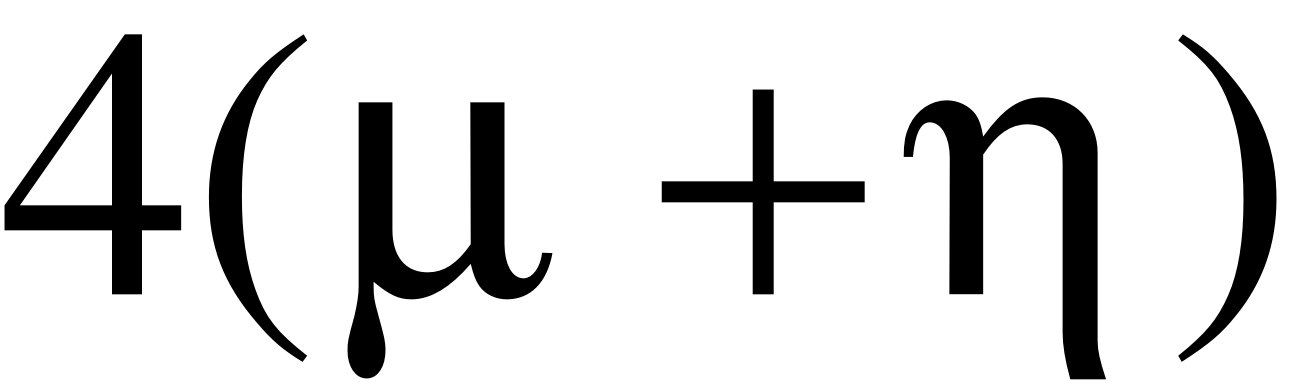
EMBED Equation.3 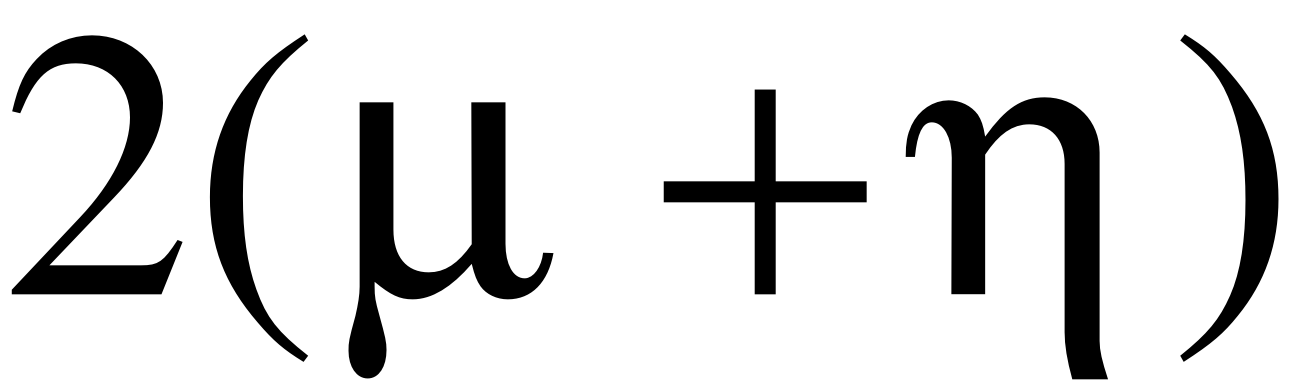
EMBED Equation.3 
EMBED Equation.3 
X2
X1
EMBED Equation.3 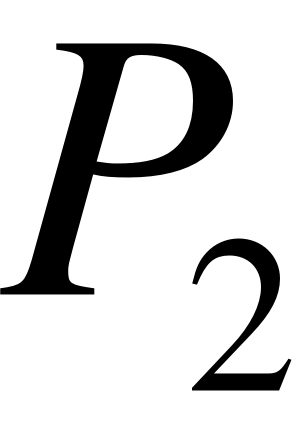
EMBED Equation.3 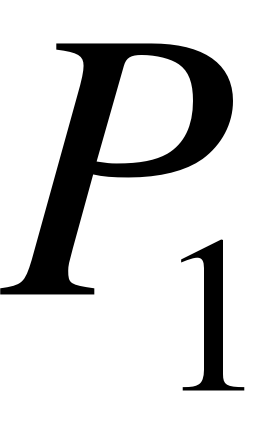
EMBED Equation.3 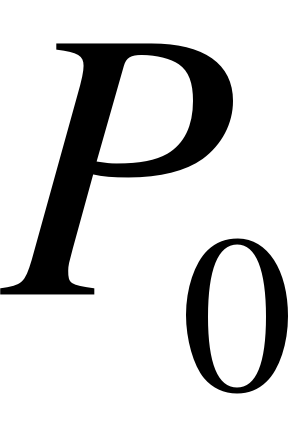
X0
Теория систем массового обслуживания