МЕТОДЫ РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ

Лекция 08

Тема. МЕТОДЫ РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ

Цель. Дать понятие о

Учебная. Разъяснить

Развивающая. Развивать логическое мышление и естественное - научное мировоззрение.

Воспитательная. Воспитывать интерес к научным достижениям и открытиям в отрасли телекоммуникации.

Межпредметные связи:

Обеспечивающие: информатика, математика, вычислительная техника и МП, системы программирования.

Обеспечиваемые: Стажерская практика

Методическое обеспечение и оборудование:

Методическая разработка к занятию.

Учебный план.

Учебная программа

Рабочая программа.

Инструктаж по технике безопасности.

Технические средства обучения: персональный компьютер.

Обеспечение рабочих мест:

Рабочие тетради

Ход лекции.

Организационный момент.

Анализ и проверка домашней работы

Ответьте на вопросы:

Что называют ложной тревогой?

Что подразумевает пропуск цели (дефекта)?

Дайте объяснение риску поставщика и риску заказчика.

Приведите формулу метода минимального числа ошибочных решений. Дайте определение неосторожного решения.

Для каких случаев предназначен метод минимакса?

Метод Неймана—Пирсона. Объясните его принцип.

Для каких целей применяется зона неопределенности?

План лекции

ЛИНЕЙНЫЕ МЕТОДЫ РАЗДЕЛЕНИЯ

РАЗДЕЛЕНИЕ В ДИАГНОСТИЧЕСКОМ ПРОСТРАНСТВЕ

МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ И МЕТОД ПОТЕНЦИАЛОВ

Одними из наиболее важных методов диагностики являются методы разделения в пространстве признаков. Эти методы основаны на естественной «гипотезе компактности», в соответствии с которой точки, отображающие одно и то же состояние (диагноз), группируются в одной области пространства признаков.

ЛИНЕЙНЫЕ МЕТОДЫ РАЗДЕЛЕНИЯ

Пространство признаков. Как уже указывалось, каждая конкретная система (объект) может быть охарактеризована вектором х в многомерном пространстве признаков:

х= {x1, x2,...,xN).

Компоненты вектора х могут быть дискретными или непрерывными величинами. Дискретные величины обычно выражают разряды (интервалы) диагностических признаков (количественных или качественных), непрерывные величины —диагностические параметры системы (температуру, давление, вибрационные перегрузки и т. п.).

Часто оказывается удобным представить объект как точку многомерного пространства (конец вектора x). Если система описывается с помощью простых (двухразрядных) признаков, то компоненты вектора выражаются двоичными числами. Тогда, естественно, каждый из объектов в пространстве простых признаков является одной из вершин единичного N-мерного куба. Например, в трехмерном пространстве объект х (011) изображается точкой, показанной на рис.1.

Во многих случаях удобно использовать трехразрядные признаки, принимая

х ={

1 наличие признака;

-1 отсутствие признака;

0 не обследовано.

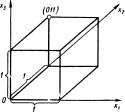
Рис. 1- Пространство простых двухразрядных признаков

Пространство признаков располагается по граням и вершинам N-мерного куба, сторона которого равна двум. Если точка (вектор) х относится к объекту (системе) с диагнозом Di-, то это записывается так:

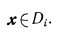(1)

Равенство (1) одновременно означает, что точка (объект) х относится к области диагноза Di в пространстве признаков.

Областью диагноза Dt называется множество точек пространства признаков (объектов), обладающих состоянием (диагнозом) Dt. Обычно, такие области заполняют достаточно компактно часть пространства признаков. Условие компактности состоит в том, что число граничных точек мало по сравнению с общим числом точек области.

Дискриминантные и разделяющие функции. Пусть в пространстве признаков (параметров) содержатся точки, принадлежащие п различным диагнозам (состояниям) D1…Dn

Дискриминантными функциями для этих диагнозов будем называть скалярные функции fx (i = 1, 2, ..., n), удовлетворяющие условию

Скаляр (от лат. scalaris — ступенчатый) — величина (возможно переменная, то есть функция), каждое значение которой может быть выражено одним числом (чаще всего подразумевается вещественное число).

Таким образом, функция ft (x) принимает для точек диагноза D1 наибольшие значения по сравнению со всеми другими дискриминантными функциями. Обозначение fx в краткой форме указывает зависимость функции от всех координат пространства х1 ..., xN; fi (x)=fi (x1 x2, ..., xN). Пример линейной дискриминантной функции для 1-го диагноза

Существенное практическое значение имеет разделение на два диагноза (состояния) D1 и D2 (например, исправное и неисправное).Этот случай часто называется дихотомией или дифференциальной диагностикой.

При распознавании двух состояний в качестве разделяющей функции можно принять разность соответствующих дискриминантных функций

Для повышения надежности распознавания применяют «пороги чувствительности»

Линейные разделяющие функции. Один из важнейших классов разделяющих функций связан с линейными дискриминантными функциями.

Методы распознавания с помощью линейных разделяющих функций называются линейными методами разделения. Диагнозы, для которых возможно такое распознавание, считаются линейно-разделимыми.

Разделяющую функцию при диагностике на два состояния можно представить в виде скалярного произведения

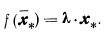
Где – весовой коэфициент

Условия разделения (решающее правило)

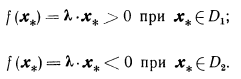
Разделяющая поверхность является плоскостью в (N + 1)-мерном пространстве или гиперплоскостью.

В практических задачах области диагнозов характеризуются обучающими последовательностями, т. е. некоторым числом объектов с заранее установленным диагнозом. В связи с этим выполнение условий линейной разделимости проверяется по обучающей выборке. Однако формулируемые ниже условия, естественно, относятся ко всей области диагноза. Так как условия разделения носят детерминистский характер:

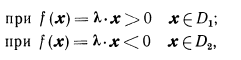
то подобное разделение возможно, если области диагнозов не пересекаются. Так как условия представляют собой строгие неравенства, то не допускается возможность касания областей. Если внутри области диагноза имеется полость или область состоит из двух замкнутых подобластей, то она не является односвязной. Достаточное условие линейной разделимости двух непересекающихся областей диагноза состоит в следующем: области диагноза должны быть выпуклыми областями. Напомним, что область называется выпуклой, если отрезок прямой, соединяющий две произвольные точки области, не выходит за ее пределы. Указанное условие можно ослабить, относя требование выпуклости только к части поверхности области, более «близкой» к другой области.

Теорема о линейном разделении содержит необходимое и достаточное условие линейной разделимости. Эта теорема формулируется следующим образом: линейное разделение областей возможно, если существует хотя бы одно направление, проекции областей на которое не перекрываются. Проекцией области на направление называется геометрическое место проекций всех точек области на данное направление.

2. РАЗДЕЛЕНИЕ В ДИАГНОСТИЧЕСКОМ ПРОСТРАНСТВЕ

Ранее рассматривались линейные разделяющие функции. Во многих случаях можно получить эффективное разделение (распознавание), используя разделяющие функции более сложного вида.

Разделяющая функция общего вида и диагностическое пространство. Рассматривается распознавание образов двух классов (диагнозов D1 и D2)с помощью разделяющей функции общего вида

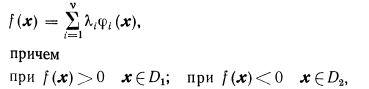
где х — вектор, изображающий объект в пространстве признаков.

Построение разделяющей функции.

Разделяющая функция будет построена, если определены коэффициенты Xt. Эти коэффициенты могут быть найдены в процессе обучения с помощью показа образцов из обучающей последовательности. Наиболее простой способ — использование алгоритмов для линейной разделяющей функции в диагностическом пространстве.

Использование диагностических комплексов (симптомов). Один из важных способов преобразования пространства признаков в диагностическое пространство — использование логических функций. Очень часто диагностическое значение имеет не наличие или отсутствие какого-либо признака, а появление или непоявление некоторого комплекса признаков.

Метод трубок дает некоторые правила, с помощью которых можно образовать диагностически ценные комплексы признаков. Объект описывается простыми признаками х1 х2, . . ., хп и представляет собой одну из вершин n-мерного единичного куба, 1 —наличие признака, 0 — отсутствие признака. Различаются два состояния D1 и D2. Для образования характерного для каждого состояния комплекса признаков используются объекты из обучающих последовательностей.

Если х0 — некоторый объект (точка в пространстве признаков), то трубкой c центром в точке х0 и радиусом r называется множество точек, для которых расстояние до центра

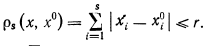
Признаки считаются существенными, если частота их появления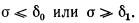

В практических расчетах можно принимать б0 = 0,3 и б1 = 0,7.

Процесс распознавания состоит в построении трубок. В трубку могут входить объекты, имеющие комплекс определенных признаков, находящийся в «окрестности» центра трубки.

Трубка называется чистой, если в нее входят некоторые из объектов данного состояния и не входят объекты другого состояния. Предъявленный для распознавания объект относится к состоянию D1 если он входит в трубки состояния D1 и не входит в трубки состояния D2.

В настоящее время достаточно эффективные общие процедуры отыскания диагностически ценных комплексов отсутствуют, однако часто инженерные и интуитивные соображения, особенно в задачах технической диагностики, помогают найти диагностически ценные комплексы и существенно снизить размерность диагностического пространства. Отметим также методы теории подобия, позволяющие образовывать безразмерные комплексы признаков.

1. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ И МЕТОД ПОТЕНЦИАЛОВ

Метод потенциальных функций является развитием идеи преобразования пространства признаков. В настоящее время метод потенциальных функций можно считать одним из наиболее разработанных и математически обоснованных методов распознавания образов (классов, диагнозов, состояний).

Основы метода потенциальных функций и метода потенциалов. В качестве дискриминантных функций f(х) для диагноза D1 в пространстве признаков в рассматриваемых методах выбираются функции, имеющие наибольшее значение для точек этой области и убывающие по мере удаления от нее. Подобным свойством обладает потенциал точечного заряда, что и дало название методам.

Метод потенциальных функций развит для разделения на два состояния (дифференциальная диагностика, дихотомия).

Диагнозы (классы) Dl и D2 считаются непересекающимися, т. е. точка х может входить только в один из указанных классов. Если известна потенциальная функция К (х, у), которую условно можно рассматривать как «потенциал» в точке х от источника в точке у, то при соответствующем выборе точек х1 и х2 можно построить разделяющую функцию. Потенциальная функция зависит от расстояния между точками:

К(х,у) = К(\х-у\).

Метод потенциалов. В этом методе для построения дискриминантных функций также используются потенциальные функции К (х,у). Однако они получаются не в результате последовательной (рекуррентной) процедуры, как в методе потенциальных функций, а строятся на основе имеющейся предварительной информации. Алгоритм построения является не самообучающимся, как в методе потенциальных функций, а заранее выбранным, детерминированным. Однако простота метода делает его привлекательным для практических приложений.

По физическому смыслу представляет собой потенциал в точке х1 от источника (заряда) в точке x2. Другой метод образования дискриминантных функций состоит в использовании среднего значения потенциальной функции

Алгоритм распознавания является обычным при использовании дискриминантных функций.

МЕТОД СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ

Этот метод, применительно к проблеме распознавания и ряду смежных проблем, позволяет оптимизировать процесс разделения в пространстве признаков.

Ранее было показано, что разделение на два состояния (класса, диагноза) в пространстве признаков может быть сведено к построению разделяющей функции f (х) и использованию правила решения

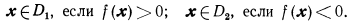
Можно усилить требования к функции потерь, считая, что она должна быть выпуклой (функцией с положительной кривизной). Построение разделяющей функции, минимизирующей погрешность приближенного решения, является оптимизацией процесса разделения в пространстве признаков. Однако применение метода минимальной погрешности в его классической форме встречает серьезные затруднения. Часть из них связана с тем, что плотность распределения р (х) обычно неизвестна и имеются только отдельные значения , входящие в обучающую последовательность.

В такой ситуации оказывается целесообразным применение метода стохастической аппроксимации.

Основной принцип сложной итерации состоит в том, что последующее приближение зависит не от одного, а от нескольких предыдущих приближений.

Домашнее задание: § конспект.

Закрепление материала:

Ответьте на вопросы:

1. На чем основаны методы разделения в пространстве признаков?
2. Опишите пространство признаков. Чем эта система может быть охарактеризована?
3. В чем состоит условие компактности?
4. Дайте пояснение линейному методу разделения.
5. Приведите достаточное условие линейной разделимости двух непересекающихся областей. Приведите пример.
6. В каком случае может быть построена разделяющая функция?
7. Опишите метод трубок, который дает некоторые правила, с помощью которых можно образовать диагностически ценные комплексы признаков.
8. Поясните физический смысл метода потенциалов.

Литература:

Амренов С. А. «Методы контроля и диагностики систем и сетей связи» КОНСПЕКТ ЛЕКЦИЙ -: Астана, Казахский государственный агротехнический университет, 2005 г.

И.Г. Бакланов Тестирование и диагностика систем связи. - М.: Эко-Трендз, 2001.

Биргер И. А. Техническая диагностика.— М.: «Машиностроение», 1978.—240,с, ил.

АРИПОВ М.Н , ДЖУРАЕВ Р.Х., ДЖАББАРОВ Ш.Ю. «ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ЦИФРОВЫХ СИСТЕМ» -Ташкент, ТЭИС, 2005

Платонов Ю. М., Уткин Ю. Г. Диагностика, ремонт и профилактика персональных компьютеров. -М.: Горячая линия - Телеком, 2003.-312 с: ил.

М.Е.Бушуева, В.В.Беляков Диагностика сложных технических систем Труды 1-го совещания по проекту НАТО SfP-973799 Semiconductors. Нижний Новгород, 2001

Малышенко Ю.В. ТЕХНИЧЕСКАЯ ДИАГНОСТИКА часть I конспект лекций

Платонов Ю. М., Уткин Ю. Г.Диагностика зависания и неисправностей компьютера/Серия «Техномир». Ростов-на-Дону: «Феникс», 2001. — 320 с.

PAGE \* MERGEFORMAT 5

МЕТОДЫ РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ПРИЗНАКОВ