РАСЧЕТ ЖЕЛЕЗОБЕТОННОЙ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ ПОДКРАНОВОЙ БАЛКИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра «Сооружение и ремонт ГНП и ГНХ»
Курсовой проект
по дисциплине «Строительные конструкции»
РАСЧЕТ ЖЕЛЕЗОБЕТОННОЙ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ ПОДКРАНОВОЙ БАЛКИ
0200.077634.019 ПЗ
Выполнил: ст. гр. БСТ-11-01 _________________ Хамидуллин Т.Д.
Проверил: _________________ Харисов Р.А.
Уфа 2013
Задание на курсовое проектирование
Рассчитать и спроектировать: железобетонную подкрановую балку двухпролетного здания.
Исходные данные:
Пролёт здания – 18 м;
Шаг колонн – 6 м;
Грузоподъемность мостового крана – 30 т.
1 КОМПОНОВКА ЭЛЕМЕНТОВ ЗДАНИЯ
1.1 Компоновочная схема здания
К элементам конструкции одноэтажного каркасного здания с балочным покрытием относятся: колонны, заделанные в фундаментах; балки (фермы, ригели, арки) покрытия, опирающие на колонны; плиты покрытия, уложенные по ригелям; подкрановые балки; фонари (Рисунок 1).
Высота здания принимается по высоте колонны:
высота здания Н = 13.2м
Размеры здания:
пролет здания L = 18 м;
число пролетов – 2;
шаг колонны LК = 6 м.
Рисунок 1 - Компоновочная схема каркаса здания
1 – колонна крайнего ряда; 2 – колонна среднего ряда; 3 – двускатная балка покрытия; 4 – подкрановая балка; 5 – ребристая плита покрытия; l – пролет здания; lK – шаг колонн; – расстояние от разбивочной оси колонны до оси подкрановой балки, равно 0,75 м; LK – пролет мостового крана; H, HB, HH, hB, hH – размеры колонны.
1.2 Подбор элементов здания и определение основных конструктивных размеров
1.2.1 Колонны
Для одноэтажных однопролетных и многопролетных зданий, имеющих пролеты до 30 м, высотой до 18 м, с фонарями и без фонарей, оборудованных мостовыми кранами грузоподъемностью до 500 кН среднего и тяжелого режима работы, при шаге колонн 6 и 12 м используются двухветьевые колонны прямоугольного сечения, марка колонн (обозначение для марки колонн: КДП – колонна двухветьевая, арабские цифры – номер колонны по несущей способности):
- крайние колонны КДП -1;
- средние колонны КДП -3.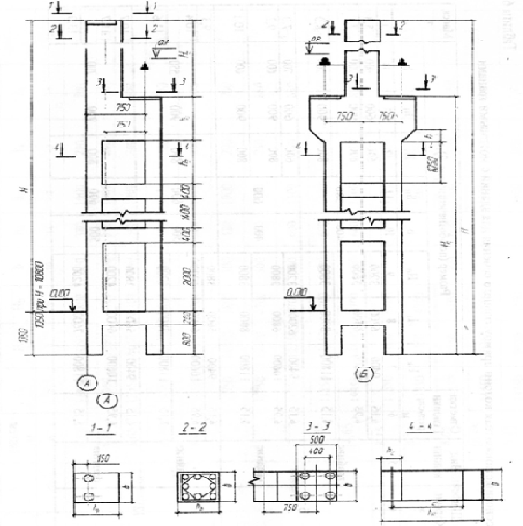 
Рисунок 2 – Колонны прямоугольного сечения.
Основные показатели выбранных колонн:
|
вид колонны
|
крайние
|
средние
|
|
марка колонны
грузоподъемность Q, кН
высота колонны Н, м
шаг колонны, м
отметка головки рельса, м
другие размеры: мм
НК
Н1
НВ
b
hВ
hН
h1
h2
масса, т
|
КДП-1
500
13,2
6
9,85
14550
9850
4700
500
380
1000
200
700
8,1
|
КДП-3
500
13,2
6
9,85
13850
9450
4400
600
600
1400
300
400
16,5
|
- Плиты покрытия
Плиты для беспрогонных покрытий представляют собой ребристые панели размерами 3х12 и 3х6, которые опираются непосредственно на ригели поперечных рам здания. Продольные ребра таких плит армируются напрягаемой стержневой или канатной арматурой, поперечные ребра и полки – сварными каркасами и сетками.
Учитывая, что по заданию шаг колонн составляет 6 м, принимаем ребристую плиту покрытия размером 3х6 со следующими характеристиками:
ширина bП = 2980 мм;
длина lП = 5970 мм;
высота hП = 305 мм;
объем бетона VП = 1,07 м3;
масса плиты mП = 2,65 т.
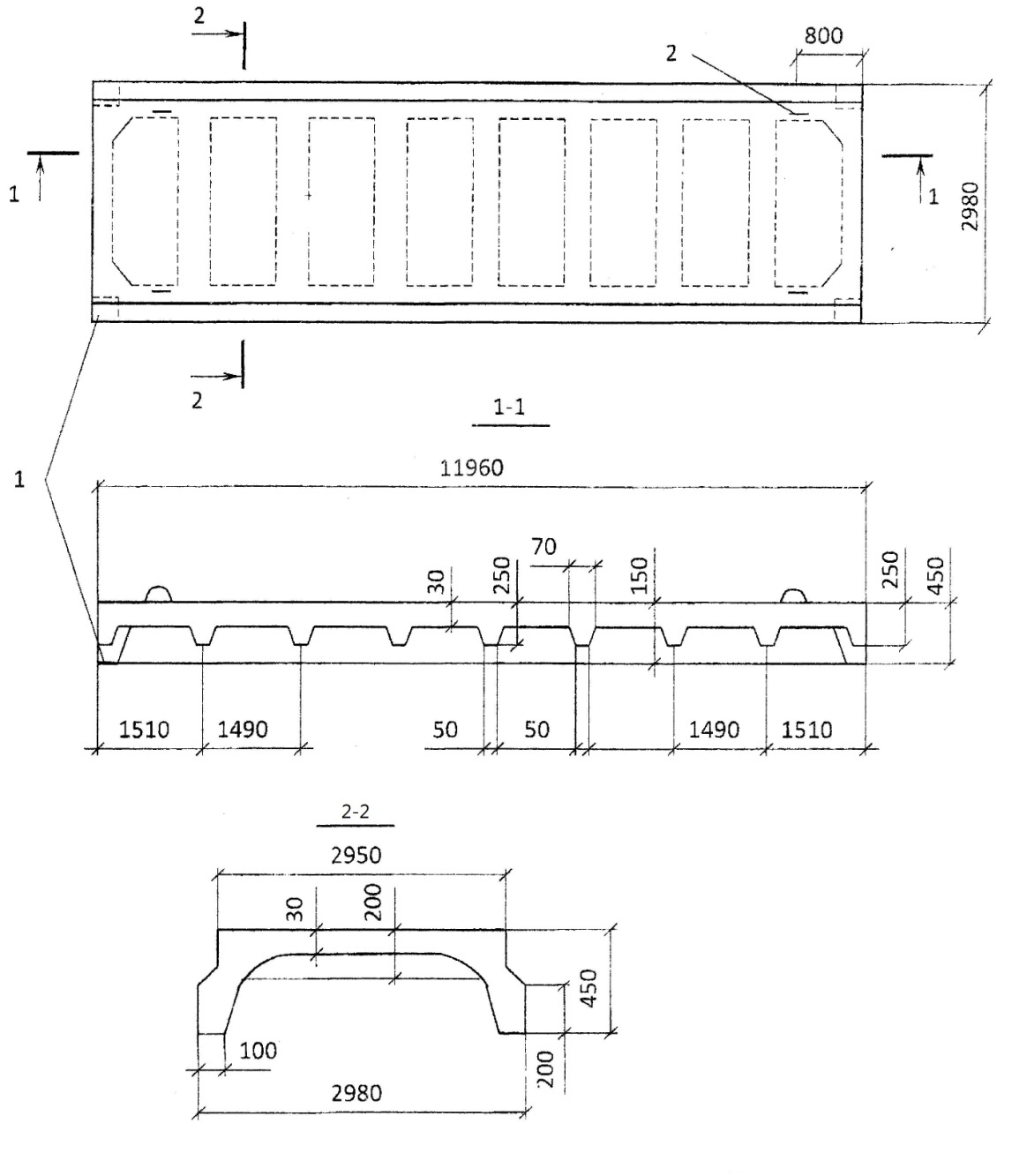
Рисунок 3 – Плита покрытия.
- Подкрановые балки
Железобетонные предварительно напряженные подкрановые балки испытывают динамические воздействия от мостовых кранов, поэтому их применение регионально при мостовых кранах легкого и среднего режима работы грузоподъемностью до 300 кН. Наиболее выгодна двутавровая форма поперечного сечения подкрановой балки с развитой полкой для повышения меткости балки в горизонтальном направлении.
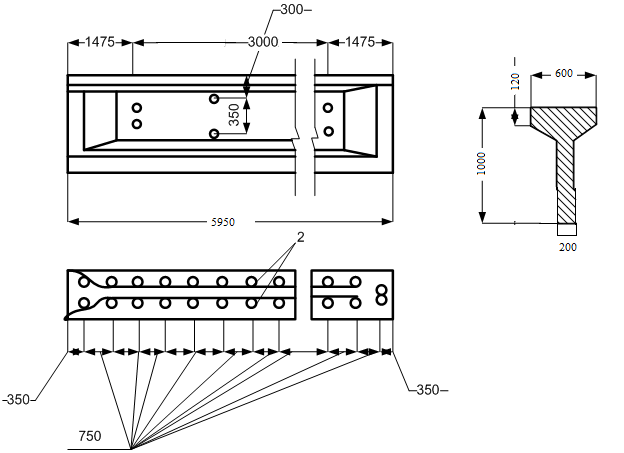
Рисунок 4 – Подкрановая балка.
Учитывая, что по заданию шаг колонн составляет 6 м, принимаем предварительно напряженную подкрановую балку со следующими характеристиками:
сечение – тавровое;
длина балки – 5950 мм;
грузоподъемность – 300 кН;
пролет – 18 м;
высота балки – 1000 мм;
верхняя ширина полок – 600 мм;
нижняя ширина полок – 0 мм;
ширина ребра – 200 мм;
верхняя высота полок – 120 мм;
нижняя высота полок – 0 мм;
объем бетона – 1,66 м3; масса балки – 4,15 т.
- Двускатная балка покрытия
Балки могут быть пролетами 12 и 18 м, а в отдельных случаях – до 24 м. Наиболее экономичная форма поперечного сечения балок – двутавровое сечение с ребром. Уклон двускатной балки принимаем 1:12. Балки выполняются из бетона марки В30– В50 и армируются проволочной, стержневой, канатной арматурой. Ребро балки армируется сварными каркасами из стержней периодического профиля.
Учитывая, что по заданию пролет здания составляет 18 м, принимаем предварительно напряженную двускатную балку со следующими характеристиками:
сечение – двутавровое;
длина балки L = 18 м;
расчетная нагрузка на покрытие q = 3,5–6,5 кН/м2;
высота сечения на опорах: hпо= 800 мм;
в середине пролета: hC = 1540мм;
высота полок верхняя hf = 220 мм;
нижняя hf = 300 мм;
ширина полок верхняя bf = 400 мм;
нижняя bf = 270 мм;
ширина ребра b = 120 мм;
объем бетона V=3,64 м3;
масса балки m = 9,1 т.
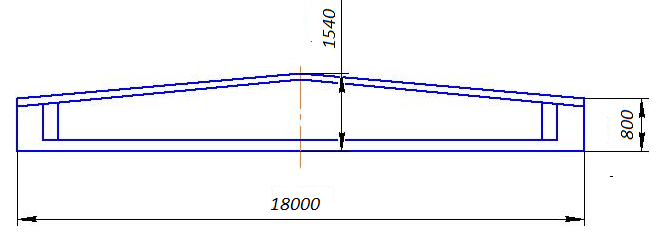Рисунок 5 – Двускатная балка покрытия.
2. Статический расчет подкрановой балки
2.1 Выбор материалов
1. Принимаем стержневую арматуру класса А- V:
для предельных состояний второй группы:
- расчетное сопротивление арматуры RS,SER =590 МПа
для предельных состояний первой группы:
- расчетное сопротивление растяжению продольной арматуры
RS=RSP=510 МПа
- расчетное сопротивление арматуры сжатию RSC=450 МПа
- расчетное сопротивление растяжению поперечной арматуры RSW=405 МПа
- модуль упругости металла арматуры Еs =1,9105МПа.
2. Бетон:
Выбираем бетон класса В30 [2].
Расчетное сопротивление для первой группы предельных состояний:
- осевое сжатие Rb ==17 МПа;
- осевое растяжение Rbt =1,2 МПа;
Расчетное сопротивление для второй группы предельных состояний:
- осевое сжатие Rb,ser =22 МПа;
- осевое растяжение Rbt,ser =1,8 МПа;
Модуль упругости бетона при растяжении и сжатии Еb= 32,5·103 МПа
Коэффициент условия работы bt=0.9;
Прочность бетона в момент обжатия принимаем:
Rbp=0,85В=0,85·30=25,5 МПа.
2.2 Расчет нагрузок, действующих на балку
На балку действуют: вес тележки мостового крана, половина веса балки мостового крана и нагрузка от собственного веса.
Примем, что нагрузка от крана приложена посередине балки. Нагрузка от веса тележки мостового крана:
кН,
где mт – масса тележки мостового крана [3];
g – ускорение свободного падения.
Нагрузка от веса балки мостового крана:
кН;
где mбм – масса балки мостового крана [3].
mбм=mк-mт=42,5-12=30,5 т,
где mк- масса крана с тележкой
Нагрузка от веса подкрановой балки:
где mБ – масса подкрановой балки;
l – длина балки.
где qНБ – нормативная нагрузка от веса подкрановой балки;
f – коэффициент надежности по нагрузке, принимаем f=1,1 (для нагрузки от собственного веса балки).
Находим суммарную нагрузку на балку от веса балки мостового крана и тележки
Находим суммарную нагрузку на балку с учетом требуемой грузоподъемности крана:
=300 кН – нагрузка от груза крана.
Так как нами принято, что нагрузки от крана приложены посередине балки, Rа=-Rв.
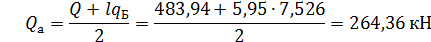
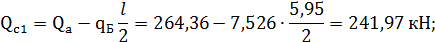
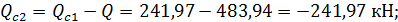
Найдем максимальный момент действующий на балку;
;
;
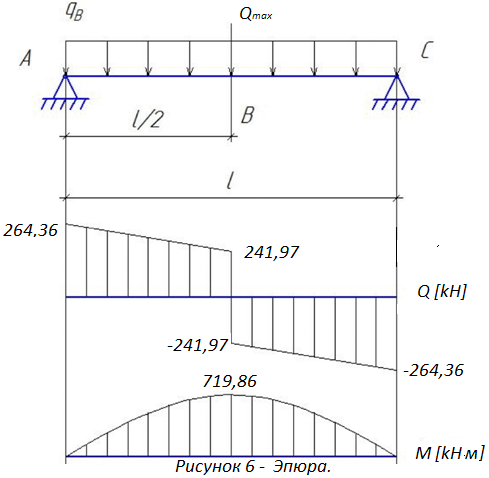
2.3 Расчет прочности балки по нормальным сечениям
Определим рабочую высоту сечения:
где h – высота подкрановой балки;
а – толщина защитного слоя бетона, принимаем а=20 мм;
f – диаметр напрягаемой арматуры, принимаем f =25 мм.
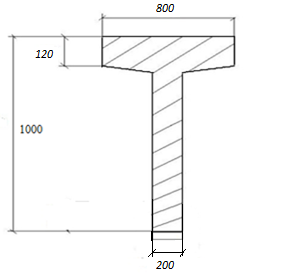
Рисунок 7 – Сечение подкрановой балки.
Рассчитаем значение относительной граничной высоты сжатой зоны бетона:
где w – характеристика сжатой зоны бетона:
w = 0,85 – 0,008·Rb = 0,85 – 0,008·17 = 0,714,
где Rb=17 МПа – расчетное сопротивление бетона сжатию;
=400 МПа – предельное напряжение в арматуре сжатой зоны.
SR – напряжение в продольной арматуре:
SR=RSP+400-SP- SP;
RSP=RS=510 МПа.
sp=0,7·Rs,ser=0,7·590=413 МПа.
Проверим выполнение следующих условий:
;
,
где р – допускаемые отклонения значений предварительного напряжения,
р=0,05·sp(при механическом способе натяжения).
Проверяем выполнение условий при р=0,05·sp=0,05·413=20,65 МПа:
413+20,65=433,65 МПа 590 МПа – условие выполняется.
413-20,65=392,35 МПа 0,3·590=177 МПа – условие выполняется.
Значение при механическом способе предварительного напряжения арматуры класса А-IV:
Тогда: SR=RSP+400-SP- SP =510+400-413-14,706=482,294 МПа.
Определим положение нейтральной линии, исходя из условия:
Условие выполняется, значит, граница сжатой зоны находится в пределах полки: хh/f и сечение рассматривается как прямоугольное, с заменой ширины b на b/f .
Вычисляем: ;
;
;
где – относительная высота сжатой зоны х/h0;
– относительная величина плеча внутренней пары сил.
Неравенство справедливо, т.к. граничные условия { и } выполняются, следовательно, при расчете по прочности железобетонных элементов с высокопрочной арматурой класса A-IV расчетное сопротивление должно быть умножено на коэффициент S6, определяемый по формуле:
где - коэффициент, принимаемый равным для арматуры класса А-IV 1,20.
Значит S6=1,20.
Определяем общую площадь сечения напрягаемой арматуры:
Определяем площадь поперечного сечения одного стержня арматуры:
.
Определяем требуемое количество стержней:
.
Общая площадь поперечного сечения стержней:
Принимаем класс арматуры A-IV.
2.4 Расчет прочности балки по наклонным сечениям
Проверяем выполнение условия:
Q K1·Rbt·b·h0;
где K1 – опытный коэффициент, принимаемый для тяжелого бетона, K1 = 0,6
493,94 кН 0,6·1,2·103·0,2·0,9675=139,3 кН.
Условие не выполняется, следовательно, в элементе появляются наклонные трещины, и его прочность по наклонному сечению должна быть обеспечена арматурой, поставленой по расчету.
Проверяем условие:
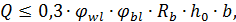
где wl - коэффициент, учитывающий влияние хомутов, нормальных к продольной оси балки, определяется по формуле:
но не более 1,3 ;
.
.
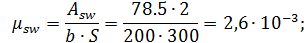
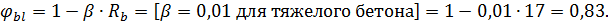
Подбираем конструктивно поперечную арматуру класса A-V, диаметром поперечных стержней d=10мм, R=545МПа, n=2. Asw=78,5мм2 - площадь поперечных стержней.
S- шаг поперечных стержней ( при h 450 мм арматура устанавливается с шагом не более h/3 = 1000/3=333.3 , S=300 мм)
Требуемое усилие, воспринимаемое поперечными стержнями, отнесенное к единице длины балки:
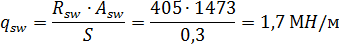
Проверим выполнение условия:
где - коэффициент, для тяжелого бетона принимается равным 0,6;
n – коэффициент, учитывающий влияние продольных сил;
.
Для предварительно-напряженных элементов вместо N подставляется усилие предварительного обжатия P:
0,5;
f – коэффициент, учитывающий влияние сжатых полок в тавровом сечении;
.
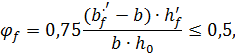
576
- условие выполняется.
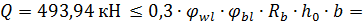
- условие выполнено.
Определяем поперечное усилие;
;
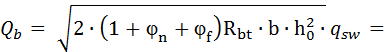
Поперечное усилие будет равно .
Расчет балки на действие поперечной силы для обеспечения прочности по наклонной трещине по наиболее опасному сечению выполняется из условия:
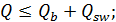
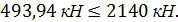
Условие выполняется, следовательно, необходимая прочность обеспечивается.
2.5 Определение геометрических характеристик приведенного сечения
Определяем отношение модулей упругости, т.е. находим коэффициент приведения:
.
Разбиваем поперечное сечение балки на два прямоугольника. Определим их площади:
;
Определяем величину х, определюящую положение нейтральной оси:
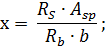
где - расчетное сопротивление арматуры растяжению.
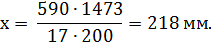
Расстояния от нулевой линии (оси) до центров тяжести рассматриваемых фигур:
Определим площадь приведенного сечения балки:
.
Определим статический момент приведенного сечения относительно нижней грани:
Расстояние от центра тяжести приведенного сечения до нижней грани:
.
Момент инерции приведенного сечения:
Момент сопротивления приведенного сечения для нижнего растянутого волокна:
;
то же для верхней грани:
.
Расстояние от центра тяжести приведенного сечения до верхней ядровой точки:
где ,
b=Rb=17 МПа – напряжение в сжатой зоне бетона;
Rb,ser=Rbn=22 МПа – расчетное сопротивление бетона по второй группе предельных состояний.
То же для нижней ядровой точки:
2.6 Потери предварительного напряжения в арматуре
Натяжение арматуры на опоры:
- первые потери:
- вторые потери:
Расчет первых потерь:
- потери от релаксации напряжения:
- потери от температурного перепада:
где t – разница температур арматуры и бетона;
- потери от деформации анкеров:
- потери от трения арматуры:
где =/6 – сумма углов поворота оси арматуры;
- потери от деформации стальных форм при изготовлении предварительно напряженных элементов с натяжением арматуры:
Суммарные значения этих потерь:
- потери напряжений от быстронатекающей ползучести для бетона, подвергнутого тепловой обработке:
где Rbp=25,5 МПа – передаточная прочность бетона;
bp – напряжение в бетоне при обжатии:
где = y0–y1= 0,2-0,158= 0,042м – эксцентриситет усилия предварительного обжатия бетона;
- усилие предварительного обжатия бетона с учетом потерь при SP =1;
Отношение удовлетворяется условию.
Суммарное значение первых потерь:
Расчет вторых потерь:
-от релаксации напряжения арматуры, напряженной на упоры:
=12,39 МПа
- потери от усадки бетона и упрочнения элемента:
- потери от ползучести бетона:
- коэффициент для бетона естественного твердения, принимаемый равным 1,0.
Суммарное значение вторых потерь:
Полные потери предварительного напряжения арматуры:
Усилие обжатия с учетом полных потерь:
2.7 Расчет по образованию трещин, нормальных к продольной оси
Расчет будем производить, исходя из условия:
МN Mcrc,
где Мcrc – момент, воспринимаемый сечением балки в стадии эксплуатаци
непосредственно перед образованием трещин в нижней части:
МN – момент внешних сил,равный нормативному моменту от внешних усилий:
Мcrc = Rbt,serWpl+Mrp,
Где Rbt,ser=1,8 МПа – расчетное сопротивление бетона (растяжение по второй группе предельных состояний);
Mrp- ядровый момент усилия обжатия.
Wpl = Wred=1,5·0,075=0,1125м3 – момент сопротивления сечения, для расчета которого принимаем =1,5.
Мcrc = Rbt,serWpl+Mrp=1,8·103·0,1125+139,7=342,2 кН·м.
Следовательно, условие МN= 654,42 кН·м < Мcrc= 342,2 кН·м не выполняется, следовательно, трещины, нормальные к продольной оси образуются.
2.8 Расчет по раскрытию трещин, нормальных к продольной оси
К балке предъявляются требования 3-й категории, т.е. допустимая ширина раскрытия трещин при действии длительной нагрузки равна 0,3 мм.
Ширина раскрытия трещин нормальных к продольной оси элемента, определяется эмпирической зависимостью:
,
где – коэффициент принимаемый равным единице для стержневой арматуры периодического профиля;
l – коэффициент, учитывающий продолжительное действие постоянных и длительных нагрузок;
– коэффициент армирования;
s – приращение напряжений от действия внешней нагрузки.
Коэффициент армирования:
.
Коэффициент, учитывающий продолжительное действие постоянных и длительных нагрузок:
.
Приращение напряжений от действия внешней нагрузки:
где z – расстояние от центра тяжести площади сечения растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне бетона:
,
где - относительная высота сжатой зоны, определяемая исходя из экспериментальной зависимости;
- дополнительный коэффициент.
Определим коэффициент:
Относительная высота сжатой зоны:
,
где =1,8 – коэффициент для тяжелого бетона равен.
Определим дополнительные коэффициенты:
;
Относительная высота сжатой зоны:
Расстояние от центра тяжести площади сечения растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне бетона:
м.
Приращение напряжений от действия внешней нагрузки:
.
Найдем ширину раскрытия трещин:
.
Сравним с предельно допускаемым значением:
0,11 мм 0,3 мм – условие выполняется, ширина раскрытия допустима.
2.9 Расчет по образованию трещин, наклонных к продольной оси
Расчет будет производиться, исходя из условия:
;
где mt – главное растягивающее напряжение;
b4 – коэффициент условий работы бетона, учитывающий влияние двухосного напряженного состояния на прочность бетона:
где = 0,01 – для тяжелого бетона;
В – класс бетона по прочности на сжатие, МПа;
В 0,3; В = 30, В = 0,0130 = 0,03, принимаем В = 0,3.
х – нормальное напряжение в бетоне на площадке, перпендикулярной продольной оси элемента, от внешней нагрузки:
у – нормальное напряжение в бетоне на площадке, параллельной продольной оси элемента, у = 0 – т.к. нет предварительного напряжения арматуры;
ху – касательное напряжение в бетоне от внешней нагрузки:
Вычислим сжимающие напряжения:
Вычислим коэффициент условий работы бетона:
Принимаем b4=1.
Проверяем выполнение условия:
- условие не выполняется, значит, трещины, наклонные к продольной оси образуются.
2.10 Расчет по раскрытию трещин, наклонных к продольной оси
Ширина раскрытия трещин, наклонных к продольной оси панели, при армировании хомутами, нормальными к продольной оси:
;
где коэффициент, равный 1,5; =1; диаметр хомутов, мм ;
напряжения в хомутах.
Диаметр хомутов в вязаных каркасах внецентренно сжатых линейных элементов должен приниматься не менее 0,25d и не менее 5 мм, где d - наибольший диаметр продольных стержней, d=25 мм.
,
где поперечная сила воспринимаемая бетоном без учета поперечных стержней;
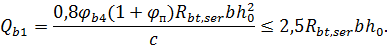
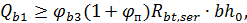
где ;
-длина проекции наиболее опасного наклонного сечения на продольную ось панели:
где - для тяжелого бетона.
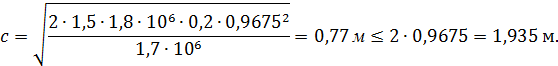
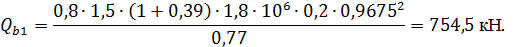
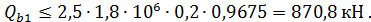
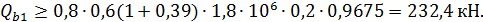
Условия выполняются, в дальнейших расчетах =754,5 кН; Q=493.94 кН.
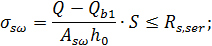
, тогда , принимаем .
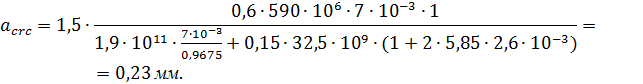
Сравним с предельно допускаемым значением:
0,23 мм 0,3 мм – условие выполняется, ширина раскрытия допустима.
2.11 Определение прогиба и кривизны балки
На участках, где не образуются нормальные к продольной оси трещины, полная величина кривизны изгибаемых, внецентренно сжатых и внецентренно растянутых элементов должна определяться по формуле:
где - кривизна соответственно от кратковременных и от постоянных и длительных временных нагрузок (без учета усилия Р), определяемая по формулам:
здесь М - момент от соответствующей внешней нагрузки (кратковременной, длительной) относительно оси, нормальной к плоскости действия изгибающего момента и проходящей через центр тяжести приведенного сечения;
jb1 - коэффициент, учитывающий влияние кратковременной ползучести бетона и принимаемый для тяжелого бетона равным 0,85;
jb2 - коэффициент, учитывающий влияние длительной ползучести бетона на деформации элемента без трещин и принимаемый равным 2.
- кривизна, обусловленная выгибом элемента от кратковременного действия усилия предварительного обжатия Р и определяемая по формуле:
.
Кривизна балки от постоянной длительной нагрузки:
Коэффициенты b1=0,85, b2=2 взяты для тяжелого бетона.
.
Тогда общая кривизна балки будет равна:
Прогиб балки определяется по формуле:
где s – коэффициент, зависящий от характера нагрузки:
s = 5/48 – при равномерно распределенной нагрузке.
Допускаемый прогиб балки:
Получается, что фактический прогиб балки меньше допускаемого, значит, подкрановая балка отвечает требованиям деформативной устойчивости.
ВЫВОД: Произведенные расчеты показали, что подкрановая балка удовлетворяет требованиям прочности и трещиностойкости по нормальным и наклонным сечениям к продольной оси балки, а также требованиям деформативной устойчивости.
3 ВЫБОР КРАНА ДЛЯ МОНТАЖА БАЛКИ
Рациональное использование кранов возможно только при правильном их выборе для монтажа конкретного объекта. Задача сводится к установлению наибольшего соответствия технических показателей грузоподъемных машин объемно-планировочным и конструктивным ремением возводимых зданий и сооружений. Непосредственно выбору предшествыет определение организационных методов монтажа, характеризующих направление и последовательность установки конструкции. При этом выясняются возможные места расположения и схемы движения кранов.
Исходные данные для подбора крана для монтажа подкрановой балки:
Масса балки: mБ=4,15 т.
Для поднятия балки применим траверсу ПИ Промстальконструкции:
Масса траверсы mс=511 кг ( Приложение 1 - Вспомогательные приспособления и оборудование для монтажа сборных конструкций).
Расчетная длина траверсы lс=5 м.
Требуемая грузоподъемность крана:
где Q= mБ - масса поднимаемого элемента, кг, Q=4150 кг
=mС=511 кг - масса такелажных приспособлений,
- масса конструкции временного усиления элемента, кг, кг;
- масса монтажных приспособлений, закрепленных на элементе, кг, кг;
Необходимая минимальная высота подъема крюка:
м,
где Нм – высота, превышение опоры монтируемого элемента под уровнем стоянки монтажного крана, м,
м;
Нк – рабочая высота колонны, м, Нк=13,2 м;
hп – высота центра крюка крана до оси оголовка стрелы, м, hп=1.5 м
hЭ – высота элемента в монтажном положении, м, hf=1,0 м;
h3 – запас по высоте, h3=0.5 м;
hтп – высота такелажного приспособления, м, hтп= lс=5 м.
Найдем высоту Н=Нкр+hп=21,2+1,5=22,7 м.
-угол наклона стрелы к горизонту;
,
где h1= Нм–hc+1 м=14,7–1,2+1=14,5 м;
b- горизонтальное расстояние от вертикали, проходящей через центр тяжести монтируемого элемента, b=18.5 м;
= arctg 0.922=43
Длина вылета стрелы и длина стрелы:
L1=h1/sin =14,5/ sin 43=21.2 м
L2=b/cos =18.5 / cos 43=25.3м
Lс= L1+ L2=21,2+25,3= 46,5 м.
Lb= L+d=Lсcos+d=46,5·cos43+1,5=35 м,
где d=1,5 м - расстояние от вращения кабины крана до начала стрелы.
Выбираем кран по следующим данным:
Qгр=4,661 т, Lс=46,5 м, Lb=35 м.
Выбираем автокран KRUPP КМК-6200.
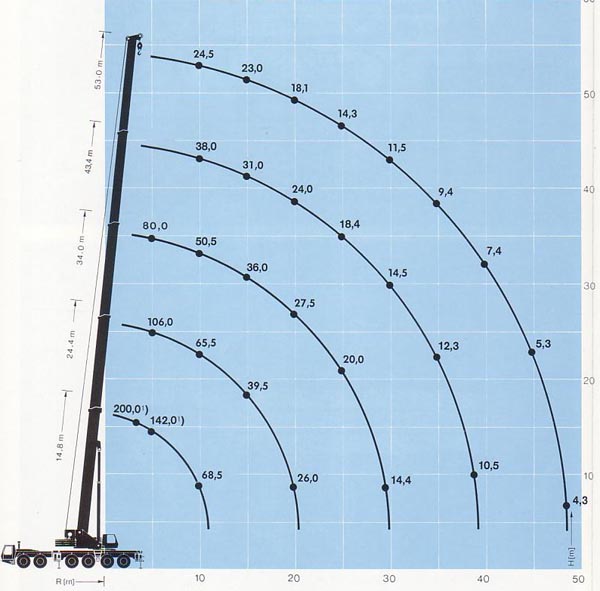
Рисунок 8 - Грузовысотные характеристики автокрана KRUPP КМК-6200.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
- Методические указания к практическим занятиям по курсу «Строительные конструкции». Компоновка элементов одноэтажного промышленного здания». – Уфа: Издательство УГНТУ, 2008г.
- СНиП 2.01.07–85*. Нагрузки и воздействия.
- СНиП 2.03.01–84*. Бетонные и железобетонные конструкции.
- Байков В.Н., Сигалов Э.Е. Железобетонные конструкции: Общий курс. Учебник для вузов. – М.: Стройздат, 1985.
- Ахметов Ф.Ш., Волохов В.Я. Каталог к подбору монтажных кранов.
- Быков Л.И., Мустафин Ф.М. и др. Строительные конструкции нефтегазовых объектов. –СПб: ООО «Недра», 2008, -780 с.
РАСЧЕТ ЖЕЛЕЗОБЕТОННОЙ ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННОЙ ПОДКРАНОВОЙ БАЛКИ