Теория вероятностей

Содержание

Введение………………………………………………………………………..3

1. Теоретическая часть
   1. Формула Байеса……………………………………………………….5
   2. Закон распределения вероятностей дискретных случайных величин………………………………………………………………...7
   3. Функции и плотности распределения непрерывных случайных величин………………………………………………………………...8
   4. Числовые характеристики важнейших непрерывных распределений…………………………………………………………9
   5. Центральная предельная теорема…………………………………..10

1. Практическая часть

Задача №1………………………………………………………………….13

Задача №2………………………………………………………………….14

Задача №3………………………………………………………………….15

Задача №4………………………………………………………………….18

Заключение…………………………………………………………………...19

Список литературы…………………………………………………………..20

Введение

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. [10]

Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине. Особенно возросла их роль в связи с развитием вычислительной техники. Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов. Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения. В этом смысле говорят, что результат измерения есть величина случайная.

Случай, случайность - с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находки, случайная ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут лет места для математики-какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности-они позволяют человеку уверенно чувствовать себя при встреча со случайными событиями.

Как наука теория вероятности зародилась в 17в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр. Слово «азарт», под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова hazard, буквально означающего «случай», «риск».[5]

Азартными называют те игры, а которых выигрыш зависит главным образом не от умения игрока, а от случайности. Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных-алгебраиста Джероламо Кардана (1501- 1576) и Галилео Галилея (1564-1642). Однако честь открытия этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым-Блезу Паскалю (1623-1662) и Пьеру Ферма. Ещё в древности было замечено, что имеются явления, которые обладают особенностью: при малом числе наблюдений над ними не наблюдается никакой правильности, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. Всё началось с игры в кости. [5]

Объект исследования – изучение алгоритмов решения задач.

Предмет исследования- применение изученных алгоритмов при решении задач.

Цель курсовой работы-решить индивидуальные задачи на основе изученного материала.

Задачи исследования:

1. Изучить основные понятия и законы в теории вероятности.

2. Научится применять основные формулы и законы теории вероятности при решении задач.

3. На основе решенных задач сделать вывод о знании понятий, формул, законов и алгоритмов решения задач по теории вероятности.

1.Теоритическая часть

1.1 Формула Байеса

Пусть события удовлетворяют условиям

, если, и .

Такую совокупность называют полной группой событий.

Пусть интересующее нас событие А может наступить после реализации одного из Hi и известны вероятности p(Hi), p(A|Hi). В этом случае справедлива формула полной вероятности

.

Пример 1. Литьё в болванках поступает из 2-х цехов: 70% из первого и 30% из второго. При этом продукция первого цеха имеет 10% брака, а второго 20%. Найти вероятность того, что одна взятая наугад болванка имеет дефект.

Решение. p(H1) =0,7; p(H2) =0,3; p(A|H1) =0,1; p(A|H2) =0,2; Р=0,7*0,1+0,3*0,2=0,13 (13% болванок в цехе дефектны).

Пример 2. В урне лежит N шаров, из которых n белых. Достаём из неё (без возвращения) два шара. Какова вероятность, что второй шар белый?

Решение. H1 – первый шар белый; р (H1) =n/N;

H2 – первый шар чёрный; p (H2) = (N-n)/N;

A – Второй шар чёрный; p (A|H1) = (n-1)/ (N-1); p (A|H2) =n/ (N-1)

Р(A)=p(H1) *p(A|H1) +p(H2) *p(A|H2) =

Формула Байеса. [8]

Предположим, что выполняются условия предыдущего пункта и дополнительно известно, что событие А произошло. Найдём вероятность того, что при этом была реализована гипотеза Hk. По определению условной вероятности

Полученное соотношение - это формула Байеса. Она позволяет по известным (до проведения опыта) p(Hi) и условным вероятностям p(A|Hi) определить условную вероятность p(Hi/А), которую называют апостериорной (то есть полученной при условии, что в результате опыта событие А уже произошло).

Пример 3. 30% пациентов, поступивших в больницу, принадлежат первой социальной группе, 20% - второй и 50% - третьей. Вероятность заболевания туберкулёзом для представителя каждой социальной группы соответственно равна 0,02, 0,03 и 0,01. Проведённые анализы для случайно выбранного пациента показали наличие туберкулёза. Найти вероятность того, что это представитель третьей группы.

Решение. Пусть H1, H2, H3 – гипотезы, заключающиеся в том, что пациент принадлежит соответственно первой, второй и третьей группам. Очевидно, что они образуют полную группу событий, причём p(H1) =0,3; p(H2) =0,2; p(H3) =0,5. По условию событие А, обнаружение туберкулёза у больного, произошло, причём условные вероятности по данным условия равны p(А/H1) =0,02; p(А/H2) =0,03; и p(А/H3) =0,01. Апостериорную вероятность p(H3/А) вычисляем по формуле Байеса:

. [8]

1.2 Закон распределения вероятностей дискретных случайных величин

Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента.

Дискретной назовём случайную величину, возможные значения которой образуют конечное множество.

Законом распределения дискретной случайной величины называется правило, по которому каждому возможному значению xi ставится в соответствие вероятность pi, с которой случайная величина может принять это значение, причём .

Пример. Абитуриент сдаёт два вступительных экзамена: по математике и физике. Составить закон распределения случайной величины х, числа полученных пятёрок, если вероятность получения пятёрки по математике равна 0,8, а по физике – 0,6.

Решение. Обозначим А1 и А2 – события, заключающиеся в том, что и математика, и физика сданы на 5. Очевидно, возможные значения х есть 0, 1, 2, причём

Полученные результаты сведём в таблицу:

xi	0	1	2
pi	0.08	0.44	0.48

. [2]

1.3 Функции и плотности распределения непрерывных случайных величин

Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента.

Непрерывной назовём случайную величину, которая может принять любое значение из некоторого промежутка.

Распределение вероятностей непрерывной случайной величины х можно задавать либо функцией распределения F(x)=p(<x), либо её производной f(x)=, называемой плотностью вероятности.

Зная F(x), можно найти плотность вероятности по формуле:

f(x)=F'(x),

а зная f(x), найдём функцию распределения:

Для непрерывной случайной величины х вероятность попадания её в промежуток с концами a и b равна:

.

Причём .

Пример. Задана следующая функция распределения:

Найти плотность распределения.

Решение.

Зная F(x), можно найти плотность вероятности по формуле:

f(x)=F'(x)= [4]

1.4 Числовые характеристики важнейших непрерывных распределений

Математическое ожидание непрерывной случайной величины определяется по формуле:

.

Дисперсия непрерывной случайной величины определяется по формуле:

.

Свойства математического ожидания и дисперсии дискретных случайных величин справедливы и для непрерывных случайных величин.

Равномерное распределение. [9]

1.5 Центральная предельная теорема

Центральная предельная теорема (ЦПТ) отвечает на следующие вопрос.

1. Когда и почему возникает в природе нормальное распределение?
2. Почему оно широко распространено в случайных явлениях природы?

ЦПТ является довольно сложным математическим результатом, но основное ее содержание может сформулировано достаточно просто. Нормальное распределение возникает в тех случаях, когда суммируется много независимых (или слабо зависимых) случайных величин Х1 , Х2,…, Хn :

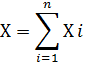
причем эти величины имеют конечные математические ожидания и конечные, сравниваемые между собой дисперсии.

Тогда каковы бы не были законы отдельных величин Х, закон распределения их суммы Х будет близок к нормальному (причем тем ближе, чем больше число слагаемых n). При достаточно больших n, можно считать, что Х € N (т,).

Становится ясно, почему нормальный закон становится распространен в технических системах: в большинстве случаев погрешности измерения параметров, отклонения вводимых управляющих воздействий и отклонения условий эксплуатации распределены по нормальному закону, так как могут быть представлены в виде суммы «элементарных отклонений», вызванных различными, практически независимыми друг от друга причинами.

Рассмотрим простейшую форму ЦПТ.

Если независимые случайные величины, имеющие одно и то же распределение (М(Х1) =

= для всех i), то при увеличении n закон распределения суммы

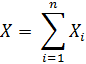
неограниченно приближается к нормальному закону распределения.

Сформулированная теорема используется в двух основных случаях: для суммы независимых случайных величин и для их среднего арифметического. [7]

Сумма независимых случайных величин. [1]

Имеем , Найдем параметры распределения случайной величины X:

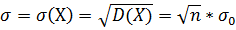
Таким образом, для случайной величины Х-суммы случайных величин -параметры нормального закона следующие:

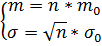
Среднее арифметическое независимых случайных величин.

Имеем . Здесь , где случайная величина Х распределена нормально, и ее параметры найдены. В этом случае

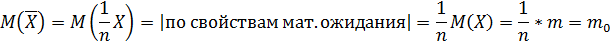
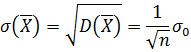
Таким образом, для случайной величины – среднего арифметического случайных величин Х-получаем:

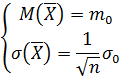
Т.е. математическое ожидание то же, что и у отдельных слагаемых Хi, а среднее квадратическое отклонение – в раз меньше. На этом свойстве основана обработка результатов физических измерений, когда усредняются результаты n независимых экспериментов: с ростом числа измерений величина становится все менее случайной, так как при . [1]

2.Практическая часть

Задача №1

Заблудившись в лесу, мальчик вышел на поляну, откуда вело 5 дорог. Известно, что для различных дорог вероятности выхода из леса за час соответственно равны 0,6; 0,3; 0,2; 0,1; 0,1. Определить вероятность того, что заблудившийся мальчик пошел по первой дороге, если известно, что он вышел из леса через час.

Решение:

А-мальчик вышел из леса через час.

=мальчик пошел по первой дороге;

=мальчик пошел по второй дороге;

= мальчик пошел по третьей дороге;

= мальчик пошел по четвертой дороге;

= мальчик пошел по пятой дороге.

Р ()= Р ()= Р ()= Р ()= Р ()=0,2

А) =0,6

(А) =0,2

(А) =0,3

(А) =0,1

(А) =0,1

Р(А)= Р()*++

Р(А)= 0,2*0,6+0,2*0,3+0,2*0,2+0,2*0,1+0,2*0,1=0,26

=

==0,46

Ответ: вероятность того, что заблудившийся мальчик пошел по первой дороге равна 0,46.

Задача №2

Рабочий обслуживает 4 независимо работающих станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго-0,75, для третьего-0,8, для четвертого-0,9. Найдите закон распределения случайной величины х, равной числу станков, которые не потребуют внимания рабочего.

Решение:

х-станок не потребует внимания.

=0 (ни один станок не потребует внимания рабочего);

=1 (1 станок не потребует внимания рабочего);

=2 (2 станка не потребуют внимания рабочего);

=3 (3 станка не потребуют внимания рабочего);

=4 (4 станка не потребуют внимания рабочего).

Р(х=0) =0,3*0,25*0,2*0,1=0,0015

Р(х=1) = =0,7*0,25*0,2*0,1+0,3*0,75*0,2*0,1+0,3*0,25*0,8*0,1+0,3*0,25*0,2*0,9=

=0,0275

Р(х=2) = =0,7*0,75*0,2*0,1+0,7*0,25*0,8*0,1+0,7*0,25*0,2*0,9+0,3*0,75*0,8*0,1+0,3*

*0,75*0,2*0,9+0,3*0,25*0,8*0,9=0,1685

Р(х=3) =0,7*0,75*0,8*0,1+0,7*0,75*0,2*0,9+0,7*0,25*0,8*0,9+0,3*0,75*0,8*0,9=

=0,4245

Р(х=4) =0,7*0,75*0,8*0,9=0,378

Ответ:

х	0	1	2	3	4
Р	0,0015	0,0275	0,1685	0,4245	0,378

Задача №3

Дана плотность вероятность f(x) непрерывной случайной величины Х. Требуется:

1. Найти параметр
2. Найти числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое, ассиметрию и эксцесс.

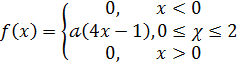
Решение:

Найдем из условия, что

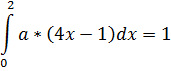
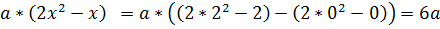
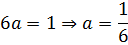
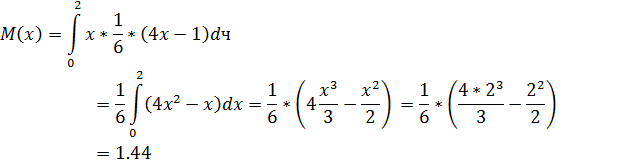
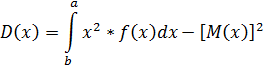
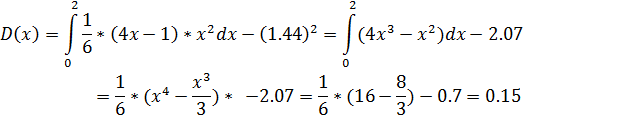
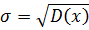
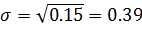
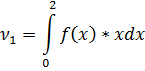
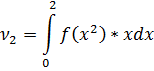
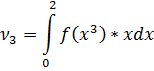
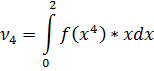
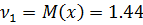
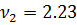
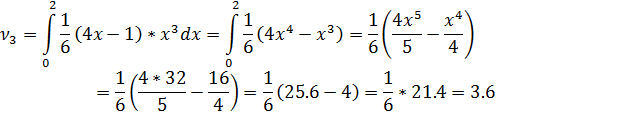
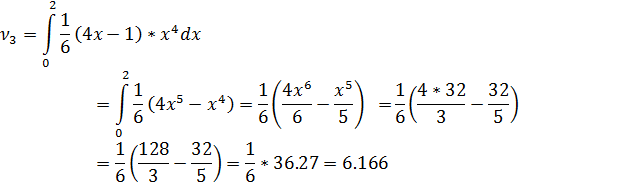
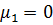
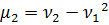
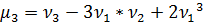
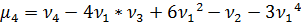
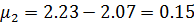
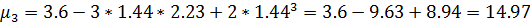
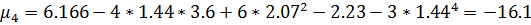
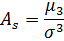
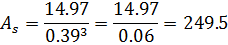
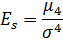
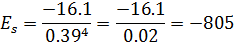
Ответ: , ,

Задача №4

Имеется 400 одинаковых микросхем, включенных параллельно в состав каскада аппаратуры. Время безотказной работы i-й микросхемы T, имеет показательное распределение, одинаковое для всех микросхем (, и измеряется в часах. При отказе i-й микросхемы каскад автоматически переключается на (i+1) -ю микросхему. Если отказали все микросхемы, то каскад выходит из строя. Выполнить грубую оценку вероятности того, что каскад проработает менее 5500 ч. Каково среднее время работы отдельной микросхемы?

Решение:

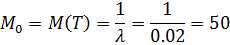
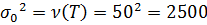
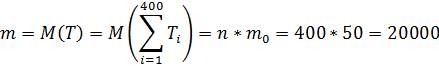
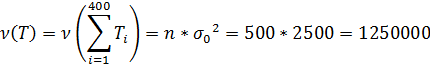
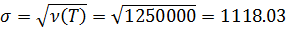
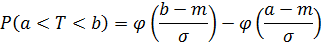
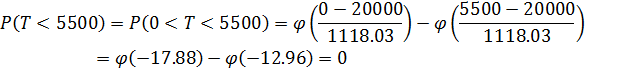
Ответ: Вероятность того, что каскад проработает менее 5500 ч,

Таким образом, скорее всего, каскад проработает дольше. Среднее время работы отдельной микросхемы каскада составляет 50ч.

Заключение

Теория вероятностей изучает закономерности, возникающие в случайных экспериментах. Случайным называют эксперимент, результат которого нельзя предсказать заранее. Невозможность предсказать результат отличает случайное явление от детерминированного. [6]

Таким образом, рассмотрев теорию вероятности, ее положения и возможности, можно утверждать, что возникновение данной теории не было случайным явлением в науке, а было вызвано необходимостью дальнейшего развития технологии и кибернетики, поскольку существующее программное управление не может помочь человеку в создании таких кибернетических машин, которые, подобно человеку, будут мыслить самостоятельно. И именно теория вероятности может способствовать появлению искусственного разума. «Процессы управления, где бы они ни протекали - живых организмах, машинах или обществе,- происходят по одним и тем же законам», - провозгласила кибернетика. А значит, и те, пусть еще не познанные до конца, процессы, что протекают в голове человека и позволяют ему гибко приспосабливаться к изменяющейся обстановке, можно воспроизвести искусственно в сложных автоматических устройствах. Важнейшим понятием математики является понятие функции, но почти всегда речь шла об однозначной функции, у которой одному значению аргумента соответствует только одно значение функции и функциональная связь между ними четко определенная. Однако в реальности происходят случайные явления, и многие события имеют не определенный характер связей. Поиск закономерностей в случайных явлениях - это задача раздела математики теория вероятности. Теория вероятности является инструментом для изучения скрытых и неоднозначных связей различных явлений во многих отраслях науки, техники и экономики.

Теория вероятности позволяет достоверно вычислить колебания спроса, предложения, цен и других экономических показателей. Также теория вероятности является основой такой науки как статистика. На формулах этого раздела математики построено так называемая теория игр.

Список литературы

1. Ахтямов, А. М. «Теория вероятностей». — М.: Физматлит, 2009
2. Вентцель Е. С. Теория вероятностей. — 10-е изд., стер. — М.: «Академия», 2005. 
3. Гмурман, В. Е. «Теория вероятностей и математическая статистика»: Учеб. пособие — 12-е изд., перераб.- М.: Высшее образование, 2006.
4. Хамитов, Г. П., Ведерникова, Т. И. «Вероятности и статистики», БГУЭП. Иркутск: 2006.
5. Чернова, Н. И. «Теория вероятностей», Новосибирск. 2007.
6. Шейнин О. Б. Теория вероятностей. Исторический очерк. Берлин: NG Ferlag, 2005.
7. Ахтямов, А. М. «Экономико-математические методы»: учеб. пособие Башк. гос. ун-т. — Уфа: БГУ, 2007.
8. Гмурман, В. Е. «Руководство к решению задач по теории вероятностей и математической статистике»: Учеб. пособие — 11-е изд., перераб. — М.: Высшее образование, 2006.
9. Чистяков В.П. Курс теории вероятностей. – СПб.: Издательство «Лань», 2006.
10. Бородин А.Н. Элементарный курс теории вероятностей и математической статистики. – СПб.: Издательство «Лань», 2006.

PAGE \* MERGEFORMAT2

Теория вероятностей