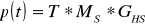Синтез стереоизображений
Лекция 10
Синтез стереоизображений
Методы наблюдения
1) делим изображение на 2, одно для левого глаза другое для правого.
Затем на экране синтезируются эти 2 изображения, в результате чего мы видим стерео изображение.
2) с помощью анаглифов:
а) цветовой (Одеваем очки со светофильтрами, допустим, синий и красный.
Наложение синий палитры на красную даст нам сиреневое изображение);
б) поочерёдное представление 2-х изображений (применяются очки в виде
оптических затворов);
в) применение очков на основе жидких кристаллов (два светофильтра, с по-
мощью изменения направления поляризации закрывается одно изображе-
ние).
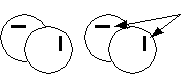
Синтез:
2 центра проекции параллельно разносятся: P-левое и Р-правое
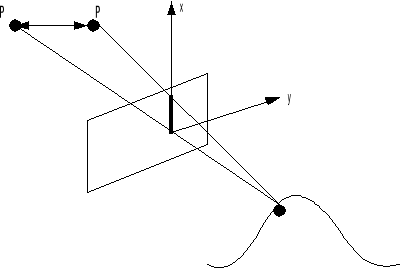
В – база
База должна
лежать в од-
ной плоскос-
ти с осью Х.
Это изображение для смещения только относительно оси Х.
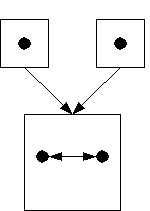
Р – продольный паралакс
10.2. Рассмотрим пример:
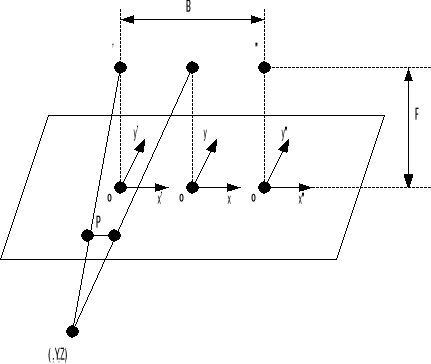
Координаты точек: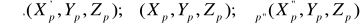 
Наблюдатель смотрит вертикально вниз.
Для центра проекции левого глаза и центра проекции правого глаза мы имеем
следующие координаты:
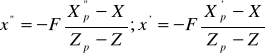
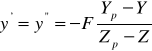
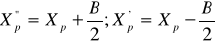
В системе координат ОХY:
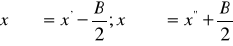
Используя эти формулы получаем:
; 
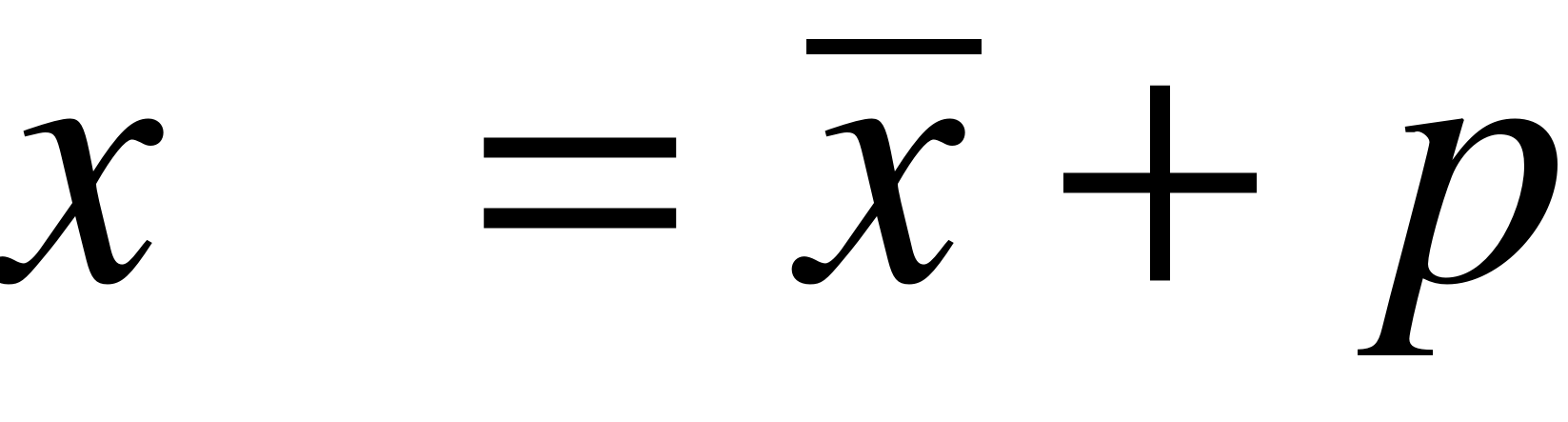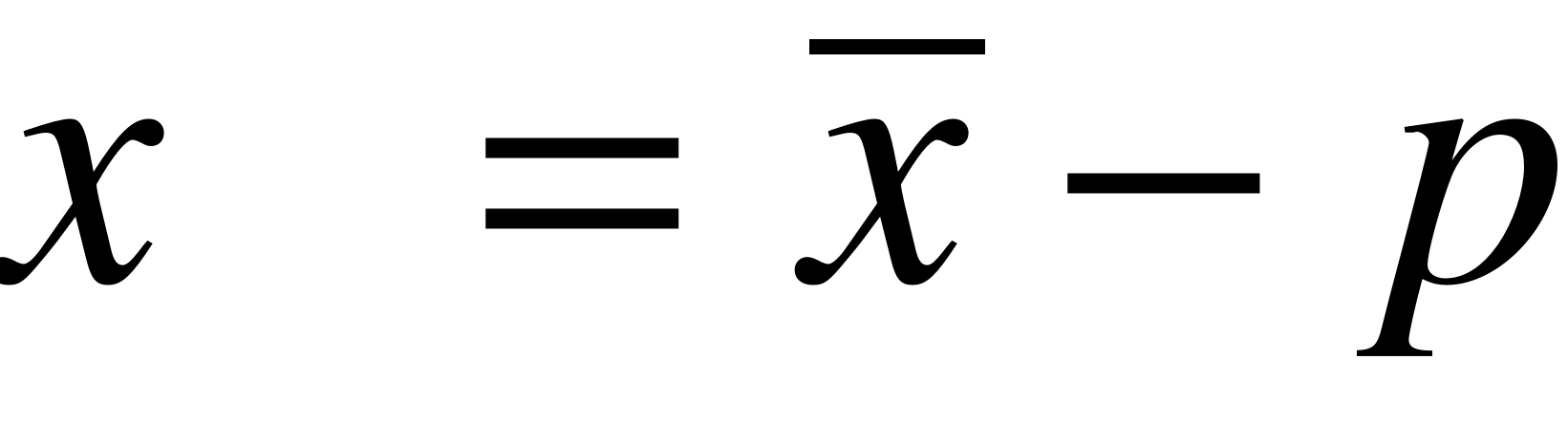, где
р – полупаралакс:
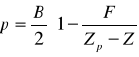, где F – фокусное расстояние
Найдём значение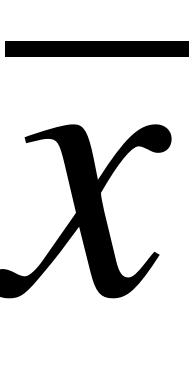 
:
; 
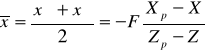
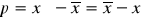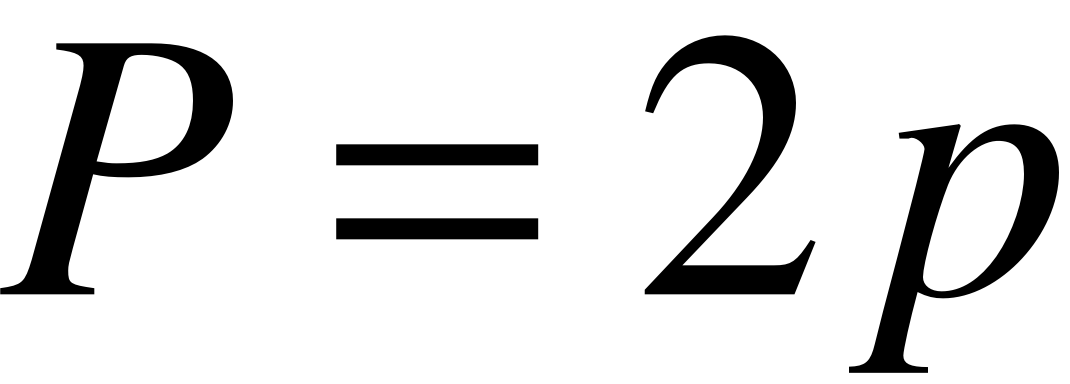
Для каждой точки можно наити изображение для левого и правого снимка.
Пусть у нас есть:
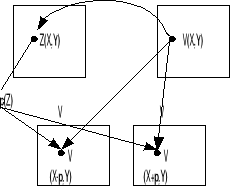
Поле высот Z(X,Y) Фотография V(X,Y)
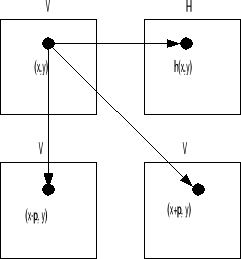
Для того чтобы получить желаемое необходимо:
Обоити все точки поля V и для каждой из них, обратившись в поле Z, получим
высоту Z(X,Y), уже имея яркость V(X,Y). Зная высоту, подставим её в формулу полупаралакса. Затем в левое поле записываем яркость V в точку (X-p,Y), а в
правое поле записываем яркость V в точку (X-p,Y).
Недостаток этого механизма:
При заполнении Vл и Vп некоторые точки могут быть не заполнены.
В качестве исходных данных мы задаём минимальный и максимальный полупа-
ралакс:
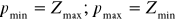
Для рассматриваемой задачи:
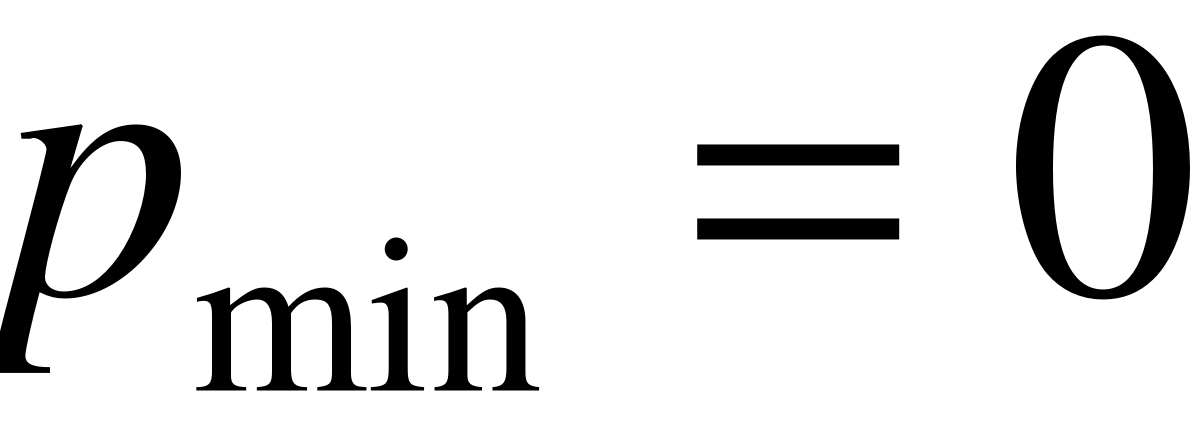
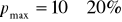от размера изображения по горизонтали (т.е. от 
)
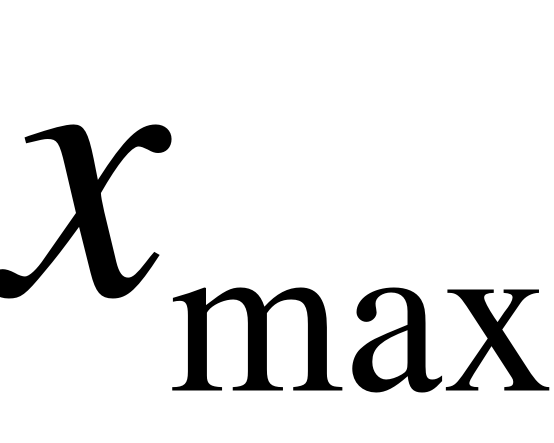Решив следующую систему, можно найти B и F:
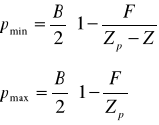
И далее подставить их в формулу полупаралакса:
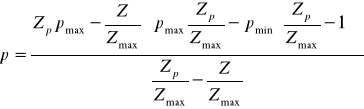, где
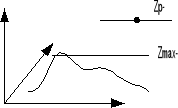
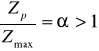, где Zp – высота наблюдателя
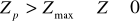
Отсюда следует следующее:
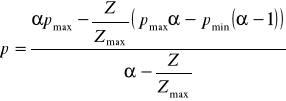
А при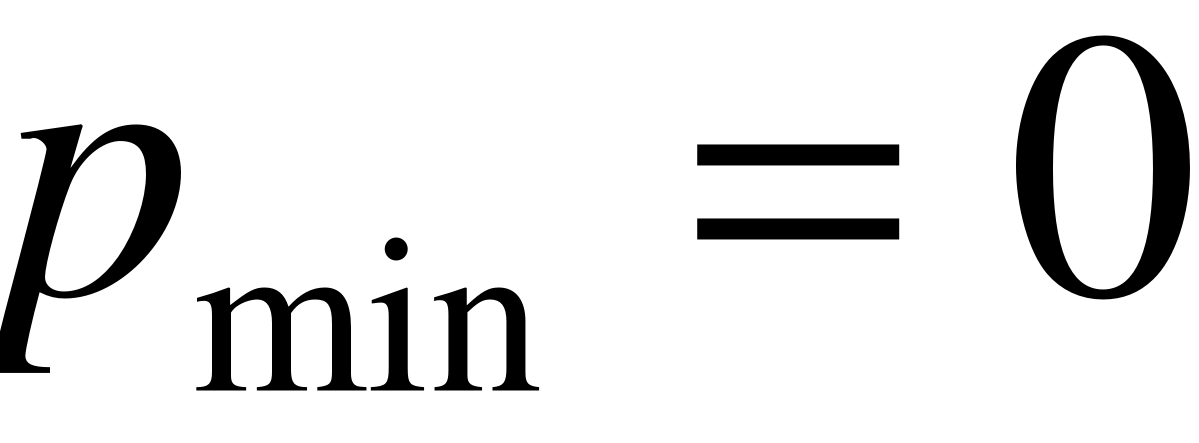 
:
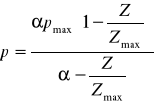
Далее вместо поля вывода будем использовать буфер глубины.
В буфере глубины содержится информация об удалённости точки от наблюда-
теля, а в поле вывода тоже фактически содержится информация об отдалённос-
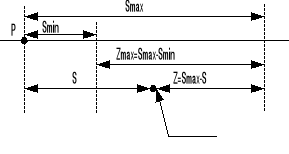
ти точки (о высоте).
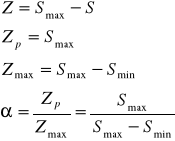
Используя формулу :
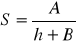, которая была получена ранее получаем, что:
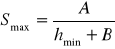, а так как 
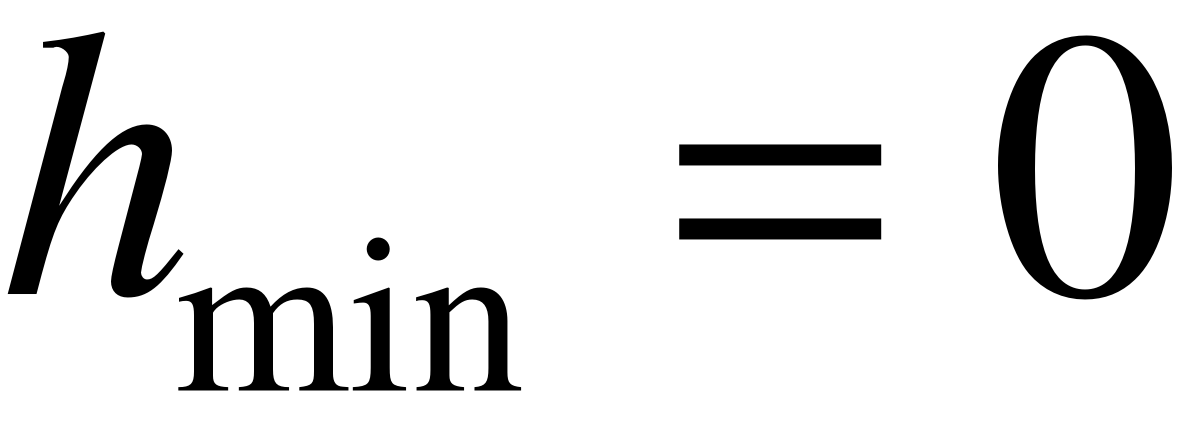, то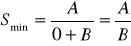 
;
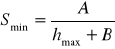
Следовательно формула полупаралакса будет выглядеть следующим образом:
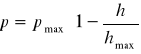
С помощью буфера глубины можно синтезировать изображение:
Представление пространственных форм.
Пусть надо изобразить пространственную кривую:
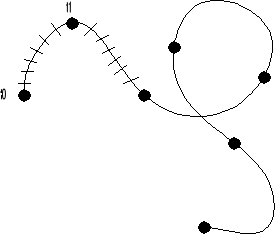
Всю кривую разобьём на криволинейные отрезки. В пределах кусочка {t0-t1}
зададим некоторый параметр t. t изменяется в диапазоне от 0 до 1.
Пространственные координаты этих кусочков:
(*)
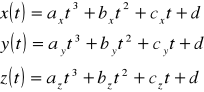Но чтобы обеспечить хорошую стыковку этих кусочков нужно соблюдать сле-
дующие условия:
1) При стыковке по уровню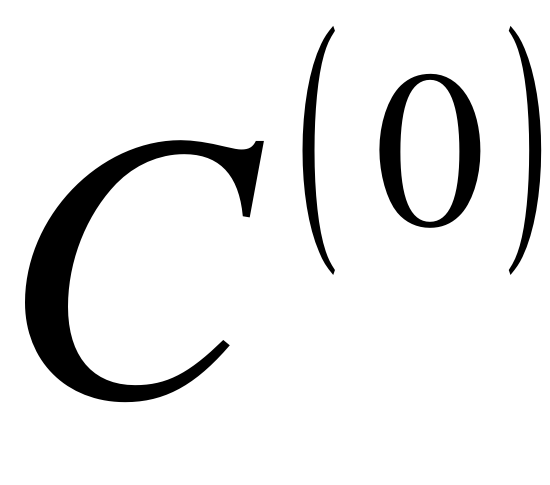 
- непрерывность по координатам;
2) При стыковке по уровню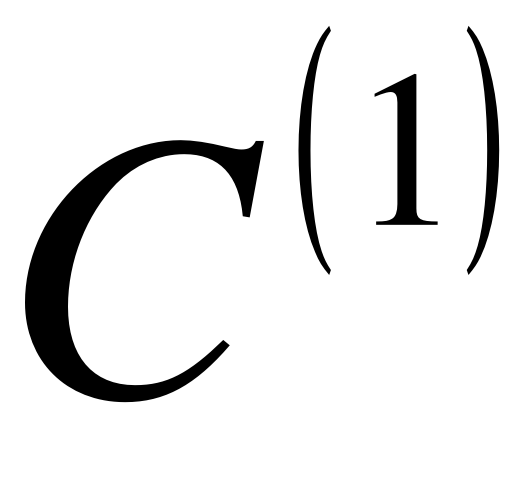 
- непрерывность по первой производной;
3) При стыковке по уровню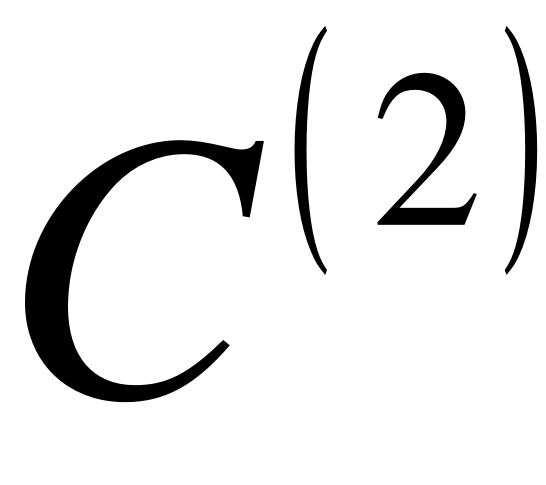 
- непрерывность на уровне второй произ-
Водной.
Математическое вычисление коэффициентов полиномов (*) см.далее
В форме Эрмита:
Для куска кривой должны быть известны:
а) координаты начальной и конечной точек:
Координаты:
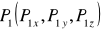и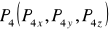 
Рассмотрим вычисления только относительно X:
; 
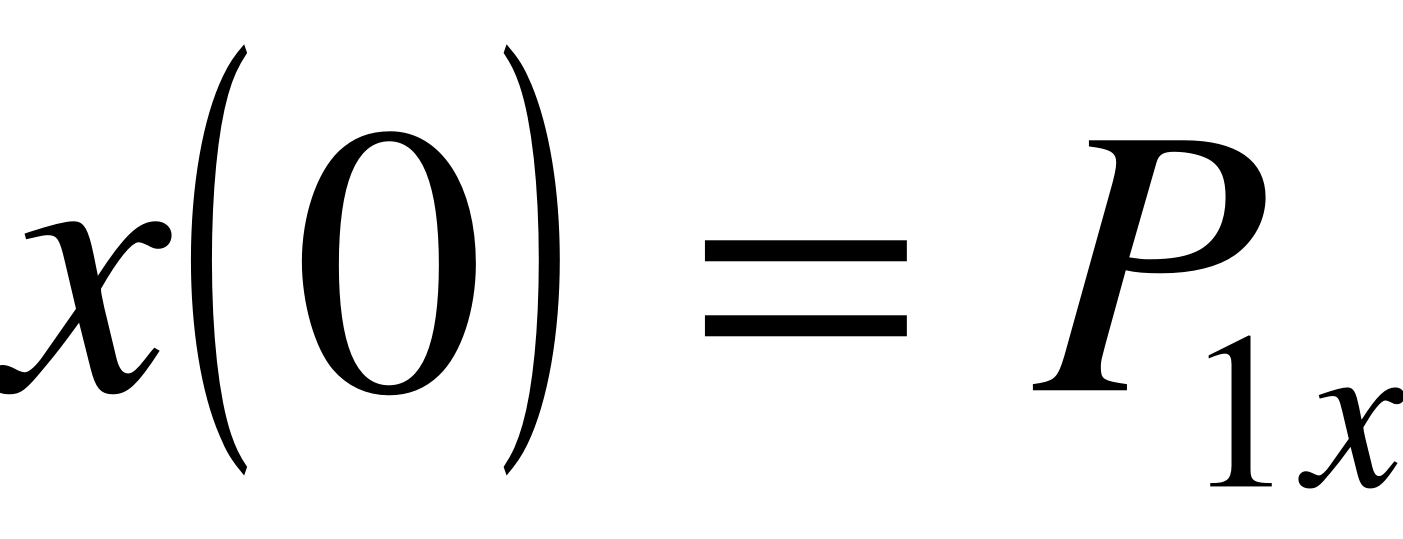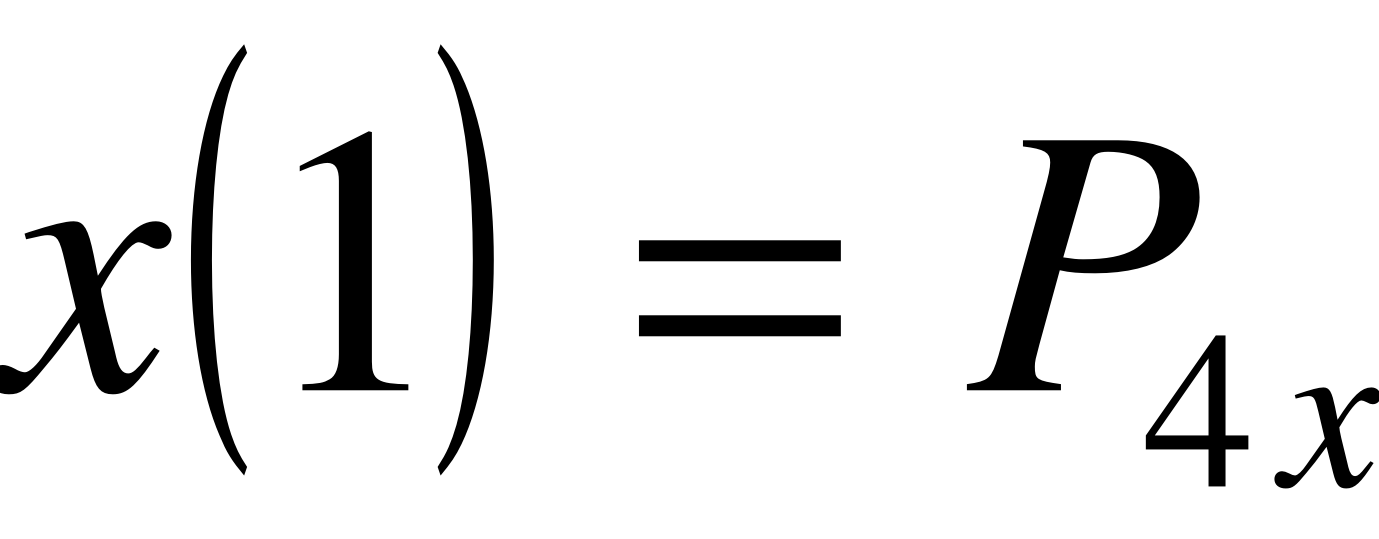
б) производные (по каждой из координат) в начальной и конечной точках:
; 
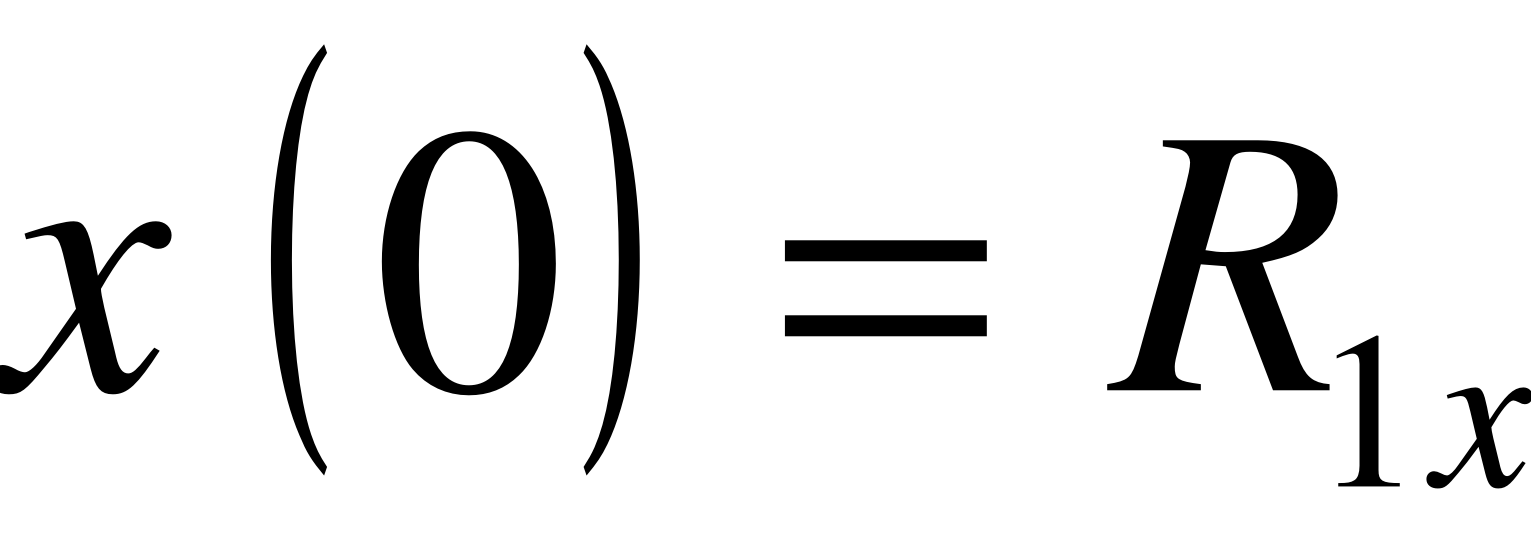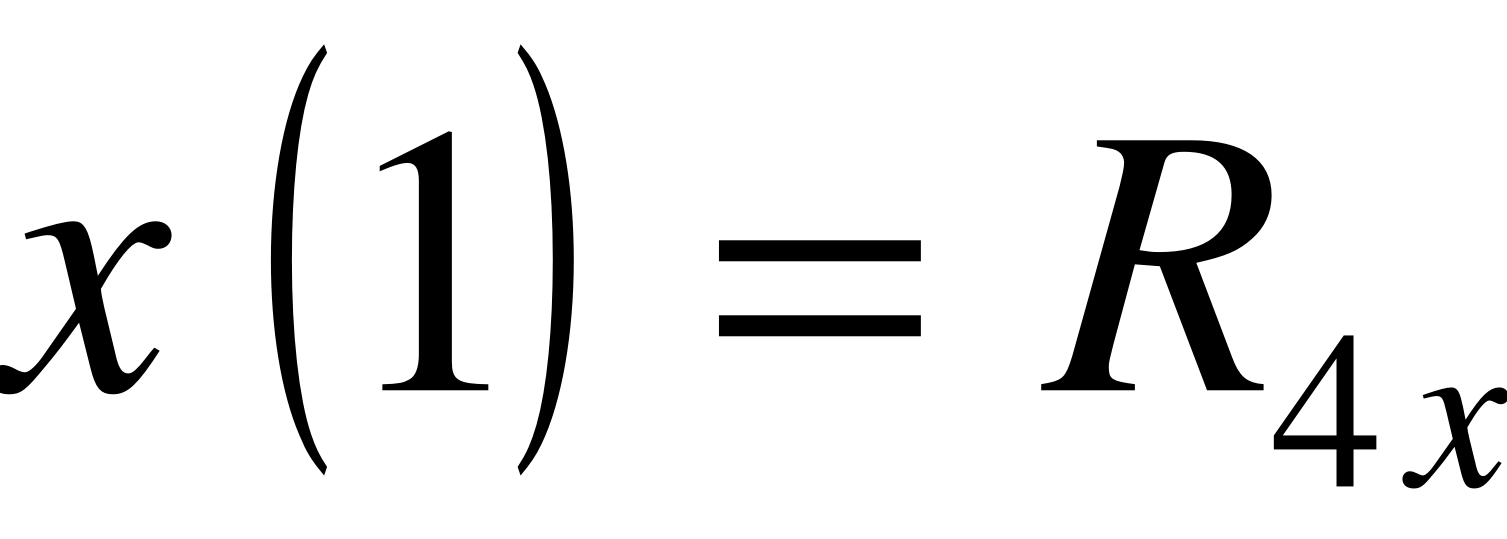
Для нахождения коэффициентов полиномов (*) обозначим:
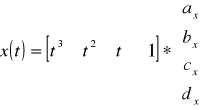
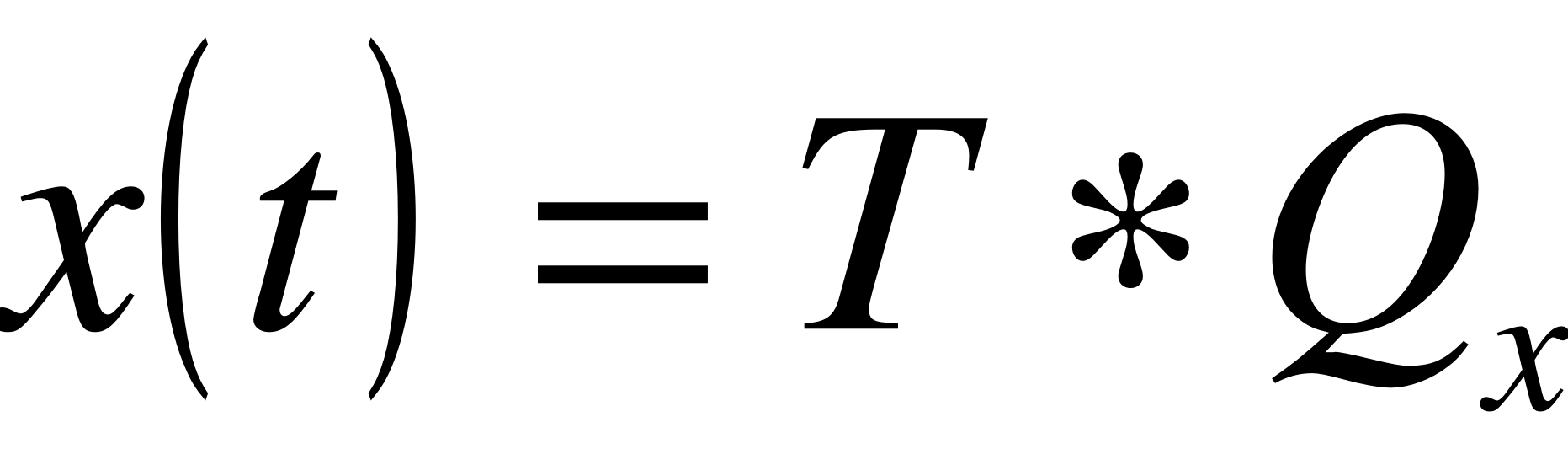, где 
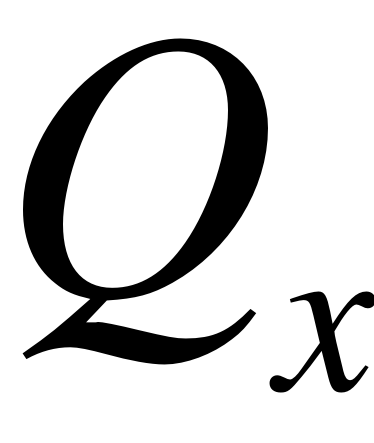- матрица коэффициентов
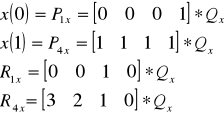
Пусть :
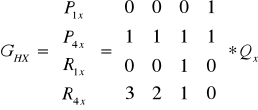
- геометрический вектор Эрмита (т.е. наши начальные данные).
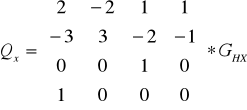
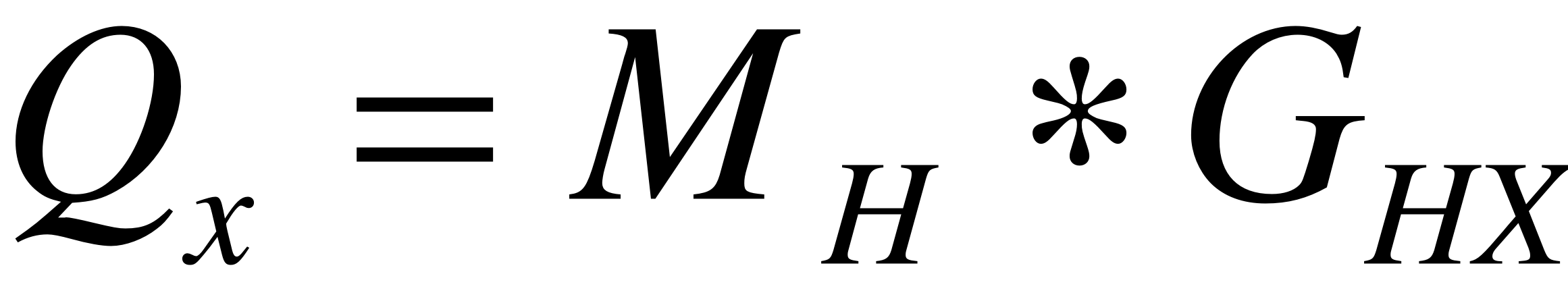, где 
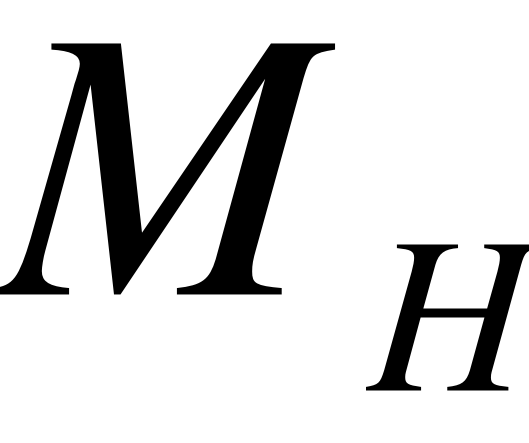- матрица Эрмитта.
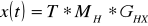
Анологичные вычисления производятся для Y и Z.
Таким образом мы получаем следующие формулы:
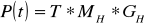и 
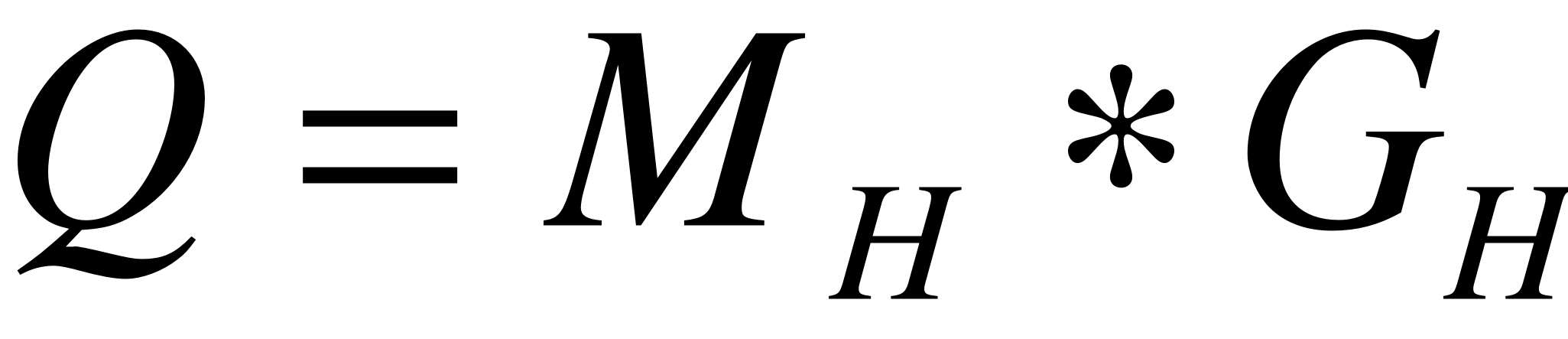
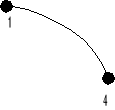
Кривая построенная по этим данным:
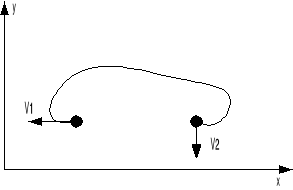
V1 и V2 – вектора скорости
Касательная к кривой задаётся от-
ношением:
Если мы хотим соединить несколько кусочков, то в месте стыковки направление касательных для конца 1-го и начала 2-го отрезков должно совпадать.
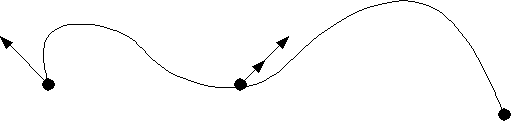
Скорости могут отличаться по длине, но они должны лежать на одной касательной.
Задание коэффициентов в форме Безье:
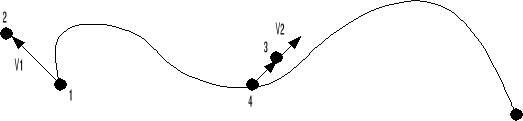
В этом случае точки 2 и 3 являются управляющими(управляют формой кривой),
а точки 1 и 4 являются опорными точками (кривая проходит через них).
Представление по Эрмиту:
; 
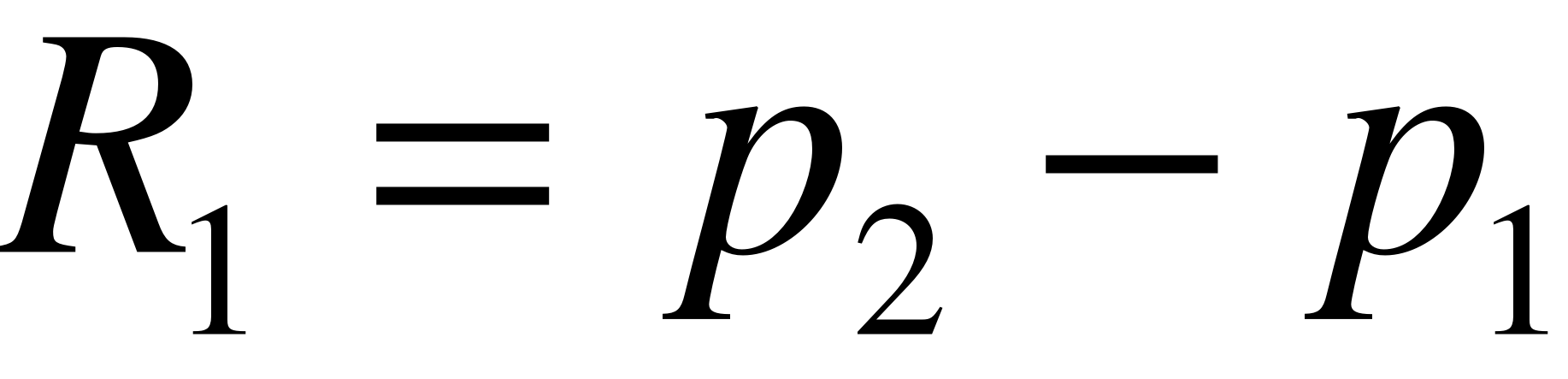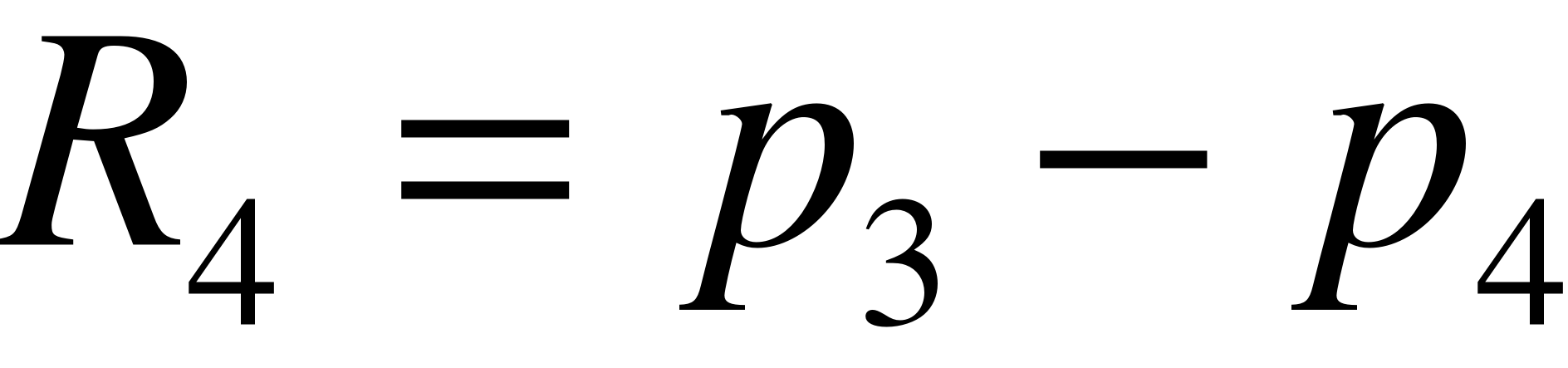
А Безье предложил следующее:
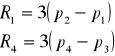
Т.е. кривая должна выити из точки 1 и прийти в точку 4, а лежать она будет вну-
три четырёхугольника, образованного точками 1, 2, 3, 4.
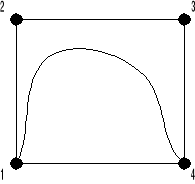
По Эрмиту:
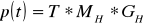, где под p может подразумеваться либо x, либо y, либо z
Запишем эту формулу для Безье:
; 
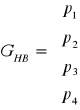Откуда следует, что:
,
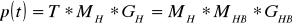где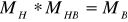 
- матрица Безье.
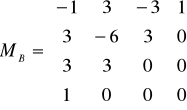
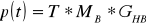, где 
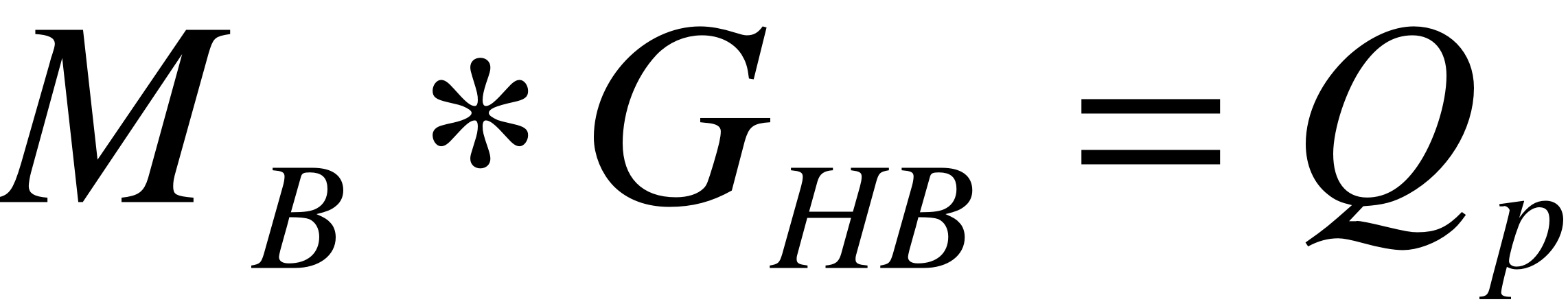- матрица коэффициентов.
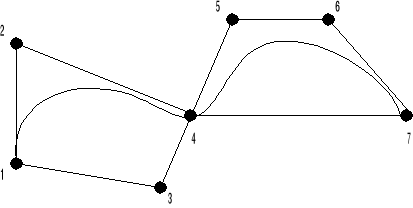
Когда мы имеем несколько кусочков кривой описанных Безье, то для стыков-
ки надо соблюсти следующее условие:
т.е точки 3 и 5 должны лежать на одной прямой (для данного случая). Это
обеспечивает одинаковую касательную в точке стыковки.
Форма сплайна:
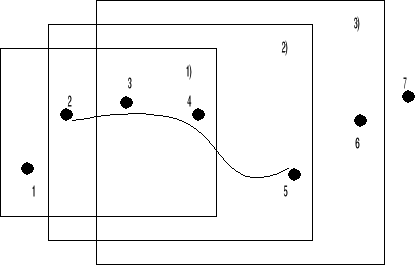
Идея: хотим провести гладкую прямую через набор точек.
Пример 1:
1) Берём первые 4-ре точки и по ним считаем уравнение кусочка кривой, но
это уравнение опишет нам кусочек кривой между точками 2 и 3.
2) Берём следующие 4-ре точки и получаем кусочек кривой между точками 3
и 4, причём можно подобрать такие коэффициенты , что в точке 3 стыков-
ка будет гладкостью 
.
Тогда:
; 
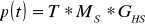
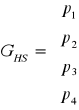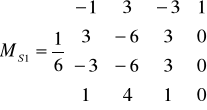
Примечание:
В рассмотренном выше примере все точки являются управляющими, т.е. кривая
проходит вблизи точек, а не по ним.
Обеспечивается гладкость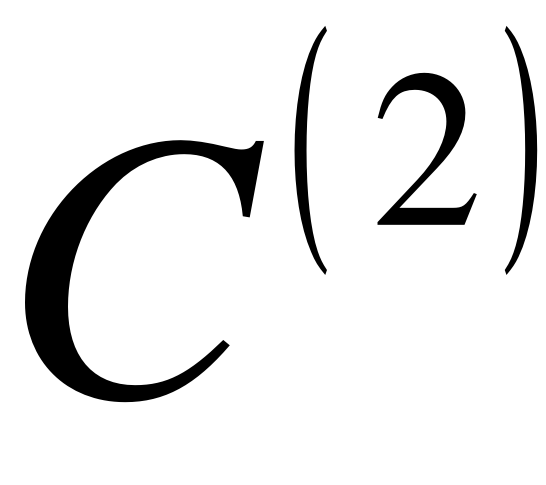 
.
Относительно решения проблемы кусочка кривой между точками 1 и 2 можно
предложить следующие варианты:
1) можно добавить фиктивные точки;
2) сделать замкнутую кривую;
3) “слить” две точки в одну.
Пример 2:
Нам нужно чтобы кривая прошла через какие-то фиксированные точки:
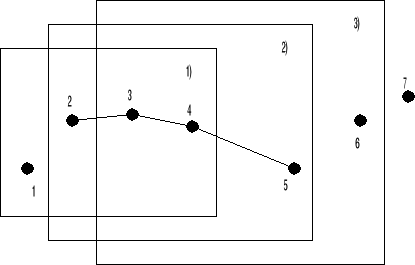
Процесс обработки тот же, что и в примере 1.
Отличие в том, что в данном случае все точки опорные и кривая проходит не вблизи , а точно по точкам. Следовательно мы проигрываем в гладкости, обеспечивая только уровень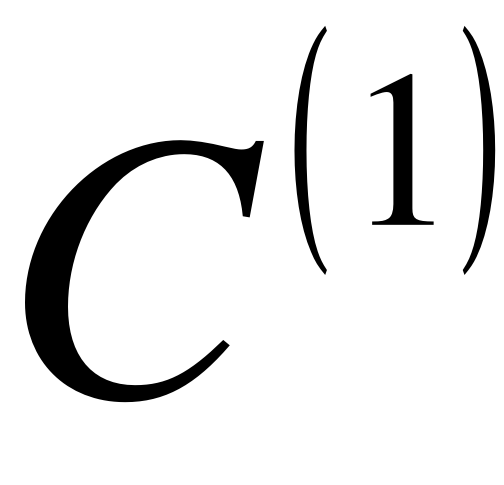 
.
Для данного случая:
; 
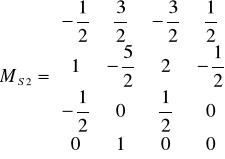Синтез стереоизображений