Моделирование освещения

Лекция 9

8. Моделирование освещения.

8.1. Основные законы освещения

8.1.1. Закон Ламберта (диффузного отражения)

Если есть некоторая поверхность и в некоторую точку этой поверхности, у которой есть нормаль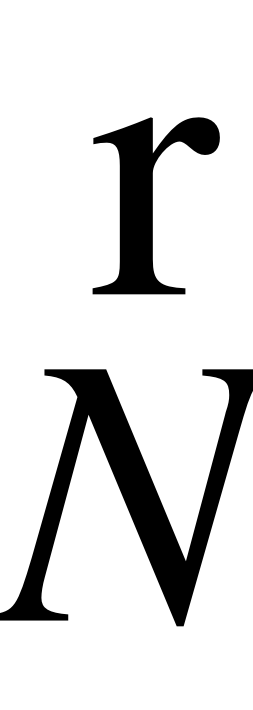, направлен луч от источника света. Для наблюдателя, находящегося в любой точке, яркость точки, которую он видит, будет выражаться следующим образом. 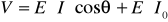, где V - яркость (для ч/б); E – альбедо (коэффициент отражения) поверхности. 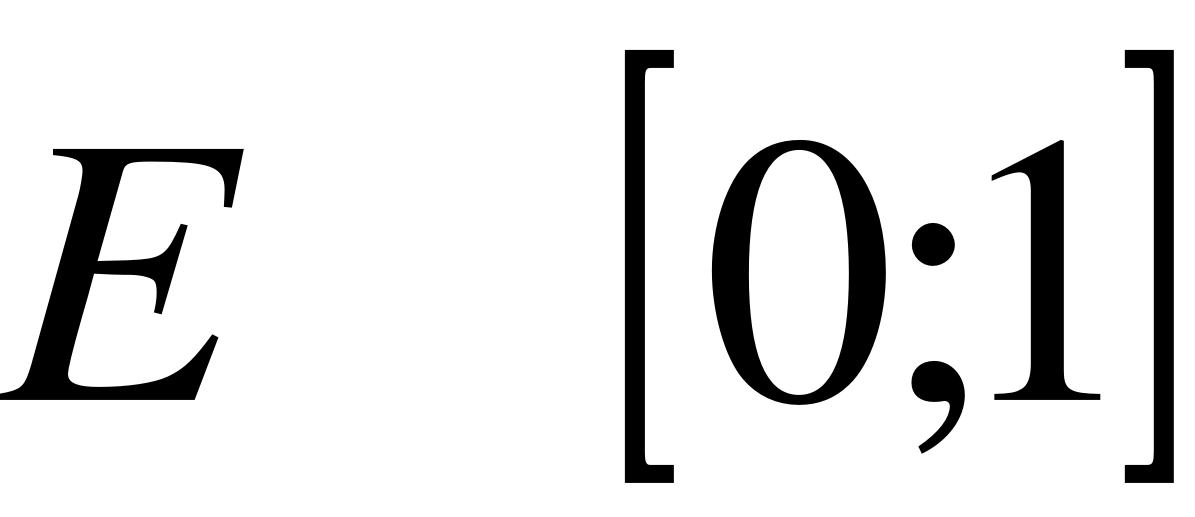, I – освещённость точки, I0 – фоновая освещенность (рассеянный свет), q - угол между нормалью (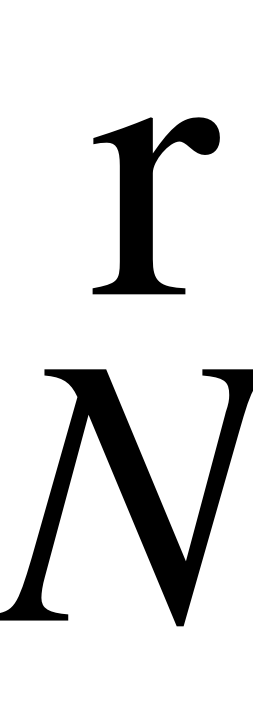) и вектором, направленным на источник света (), .

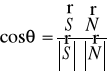Рис. 1

Данный метод не учитывает отражения света, поэтому место положения наблюдателя не играет роли. При помощи этого метода лучше всего моделируется матовые поверхности.

Рассмотренный ранее закон Ламберта можно записать в удобной форме.

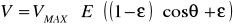где e – доля рассеянного света (рекомендуется ).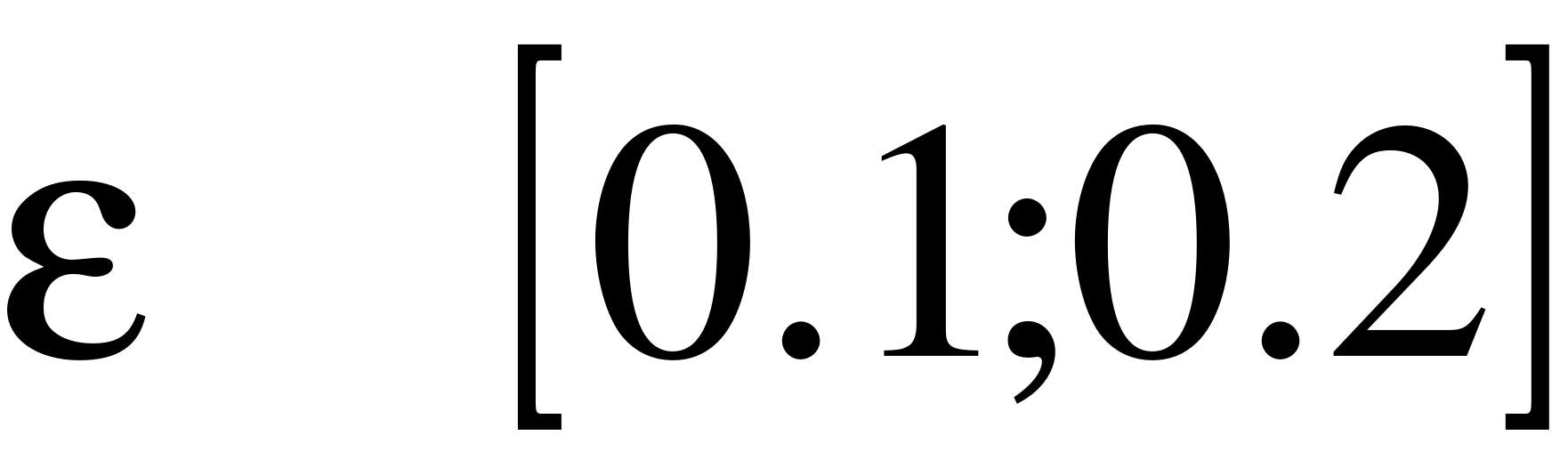

Рассматриваются два вида источников света:

а) точечный источник света:

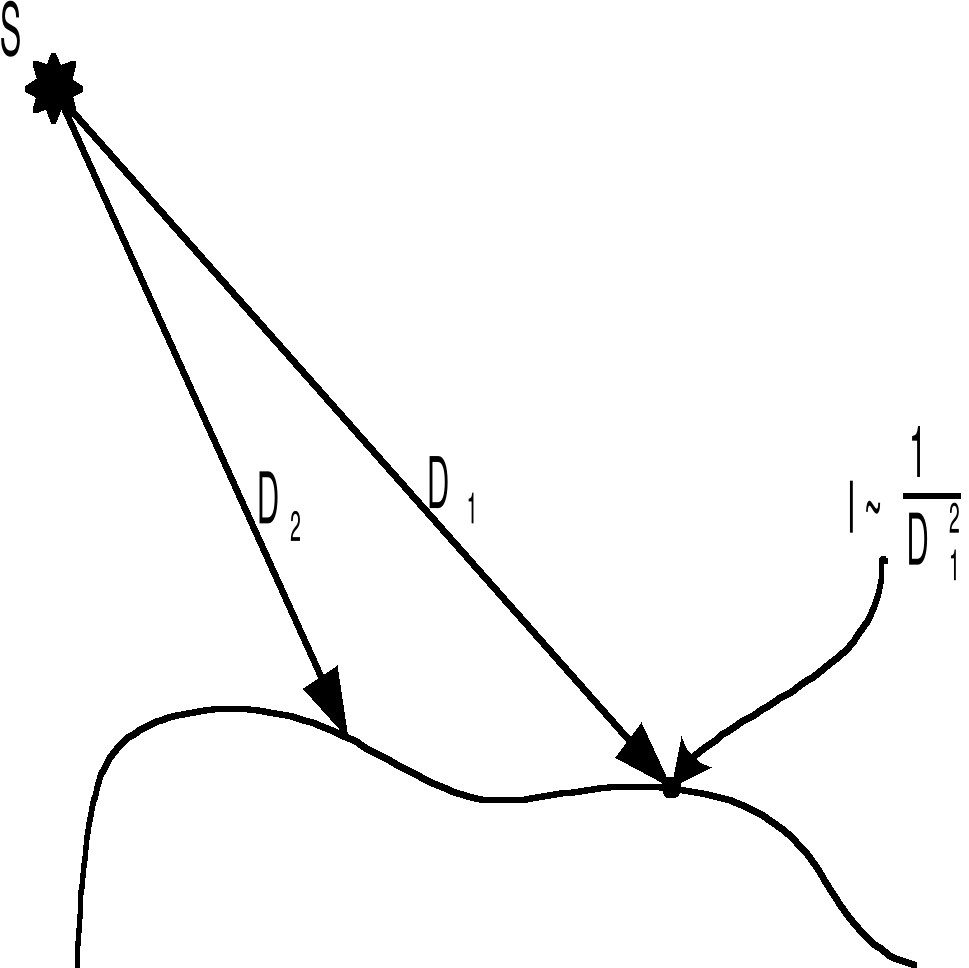
Рис. 2

б) параллельный пучок света: от удаленного источника

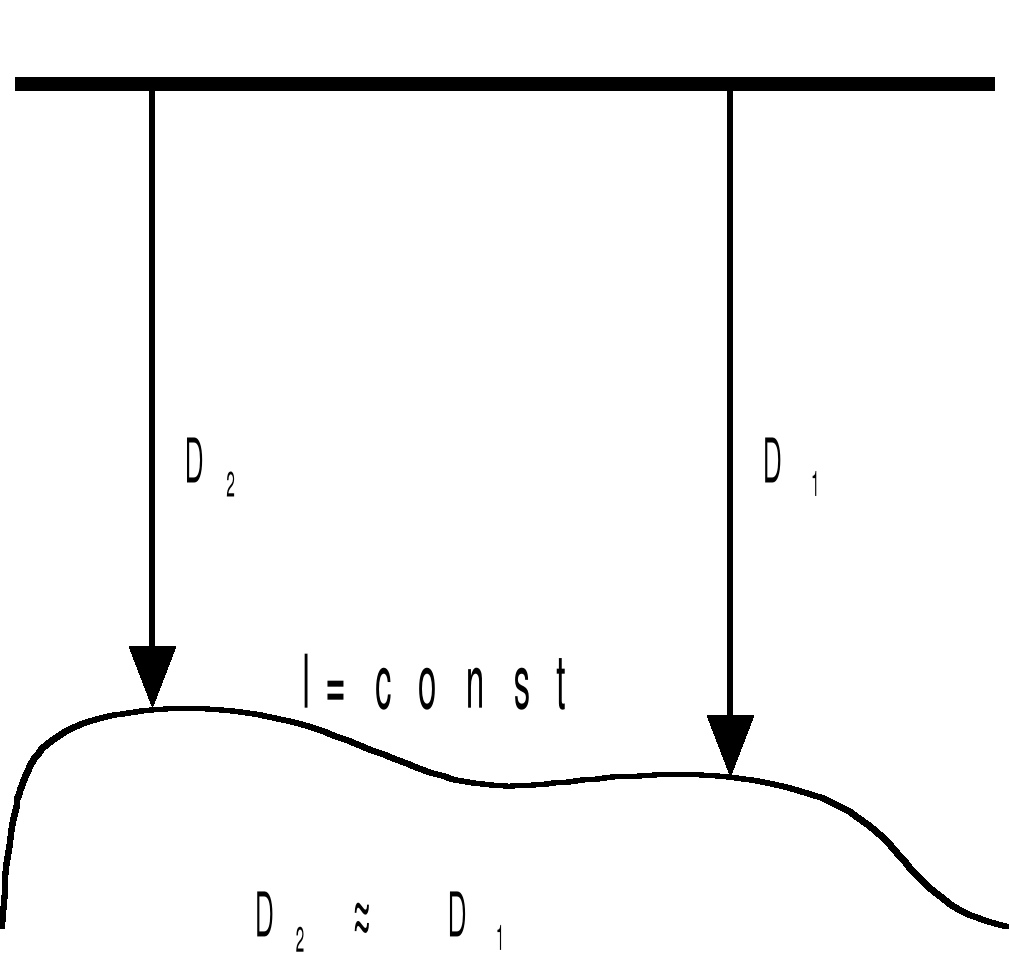
Рис.3

Закон Фонга (закон зеркального отражения)

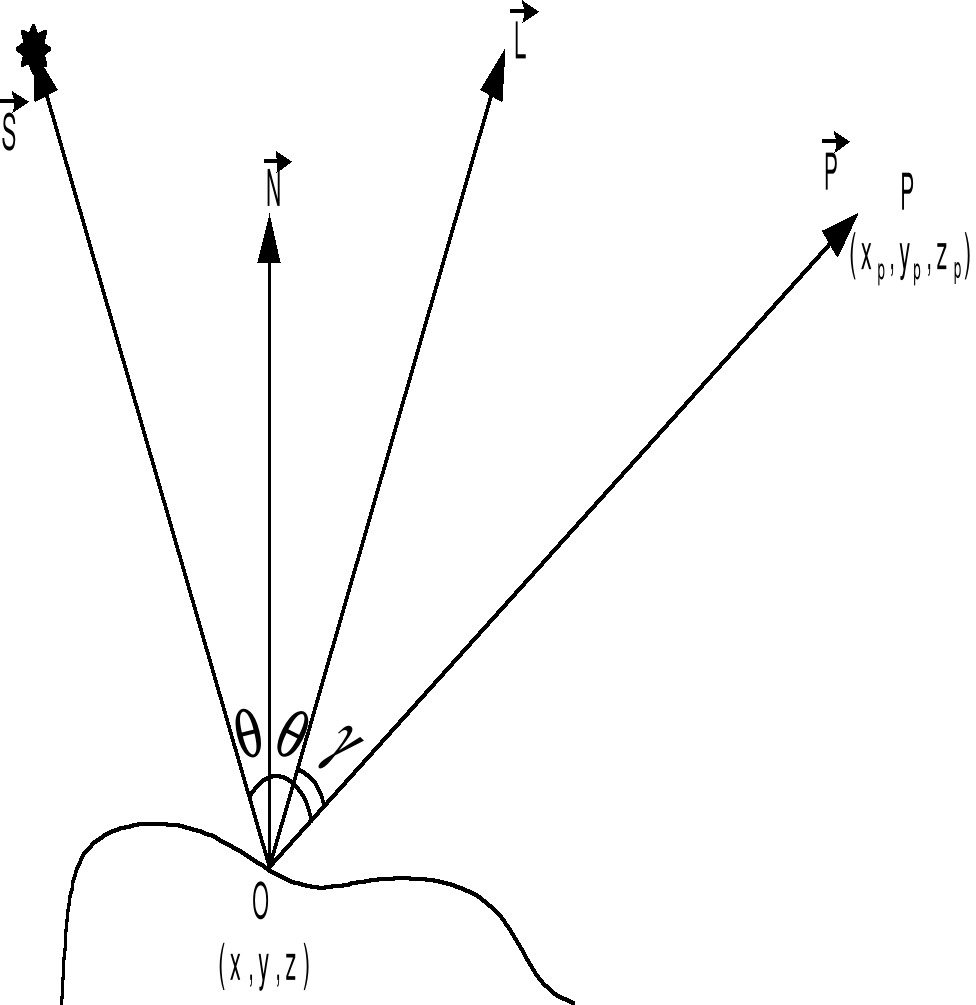
Рис.4

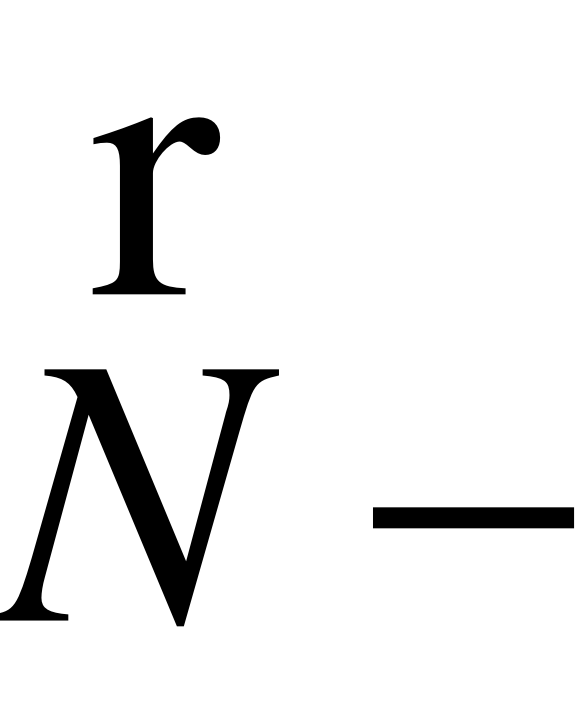нормаль к поверхности в точке (x,y,z);

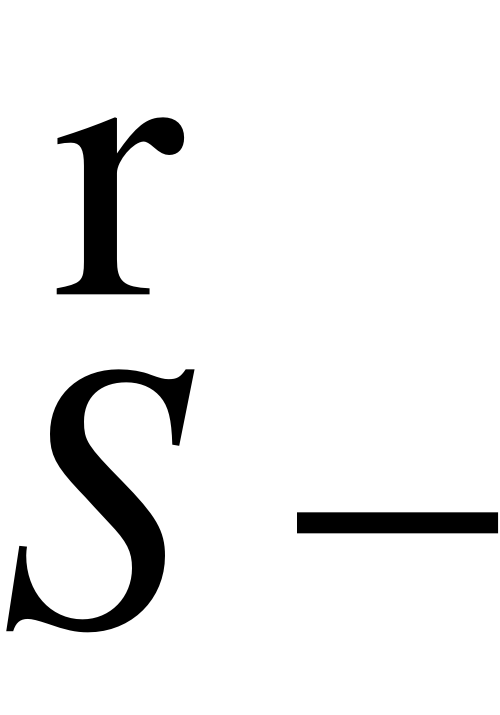падающий луч от источника S;

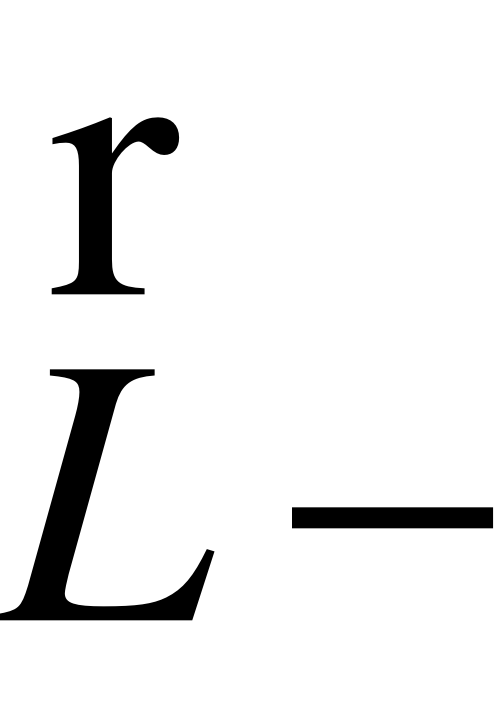отраженный луч света;

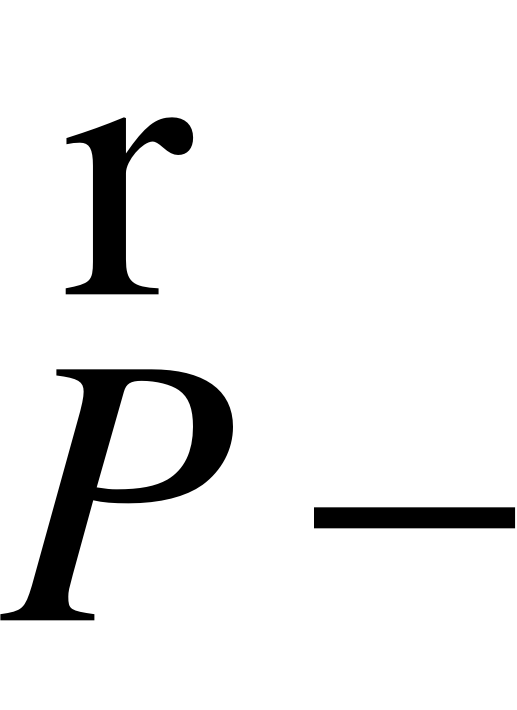направление на наблюдателя Р (xP,yP,zP);

q – угол падения и отражения;

g – угол между отраженным лучом и направлением на наблюдателя.

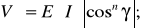формула для определения зеркальной составляющей V,

где n – степень зеркальности поверхности, 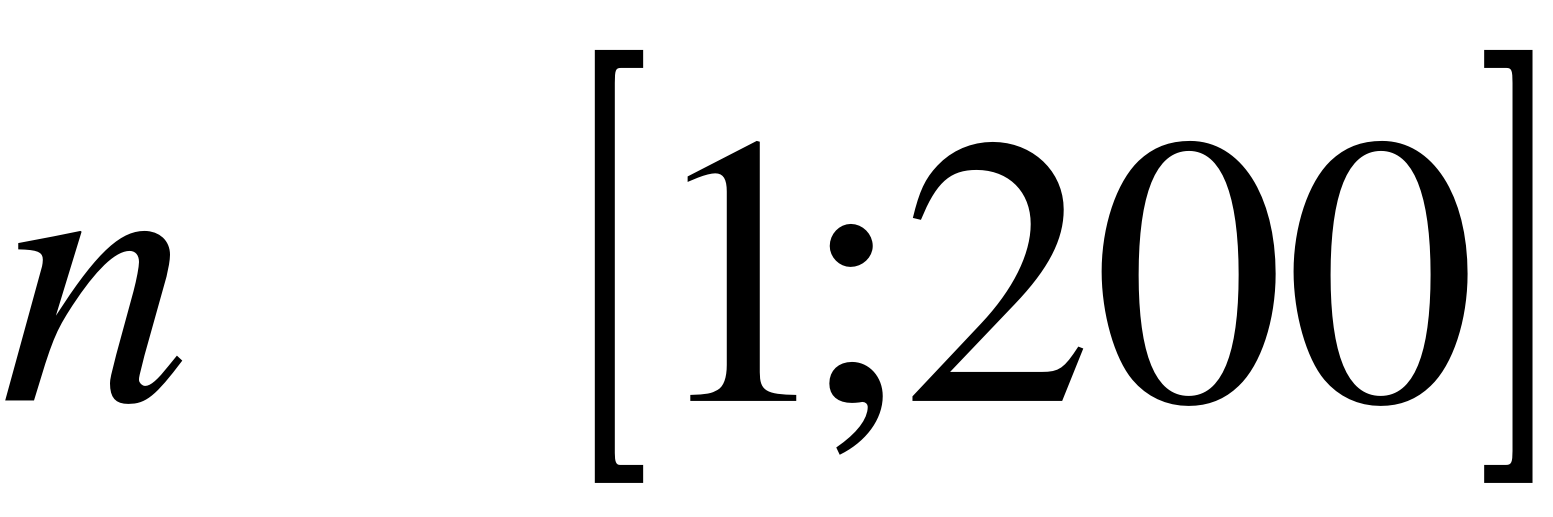. Чем больше n тем больше зеркальные свойства поверхности.

Вектора 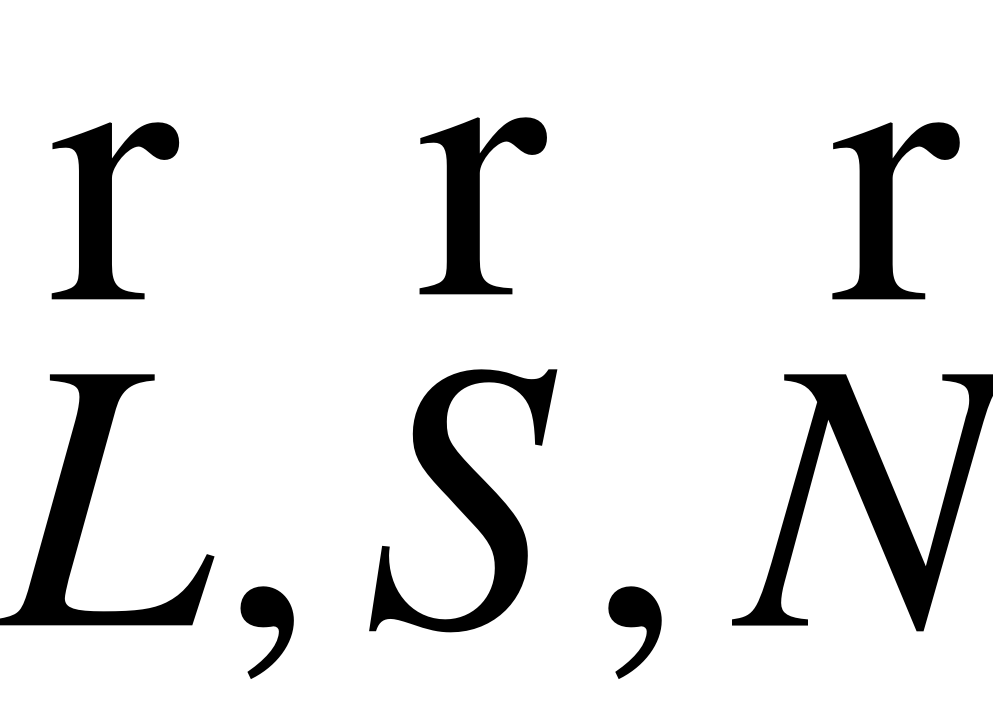нормированные и лежат в одной плоскости (см. закон отражения света)

Пусть I = const, тогда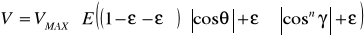

e – доля рассеянного света,

eФ – доля отраженного света, ;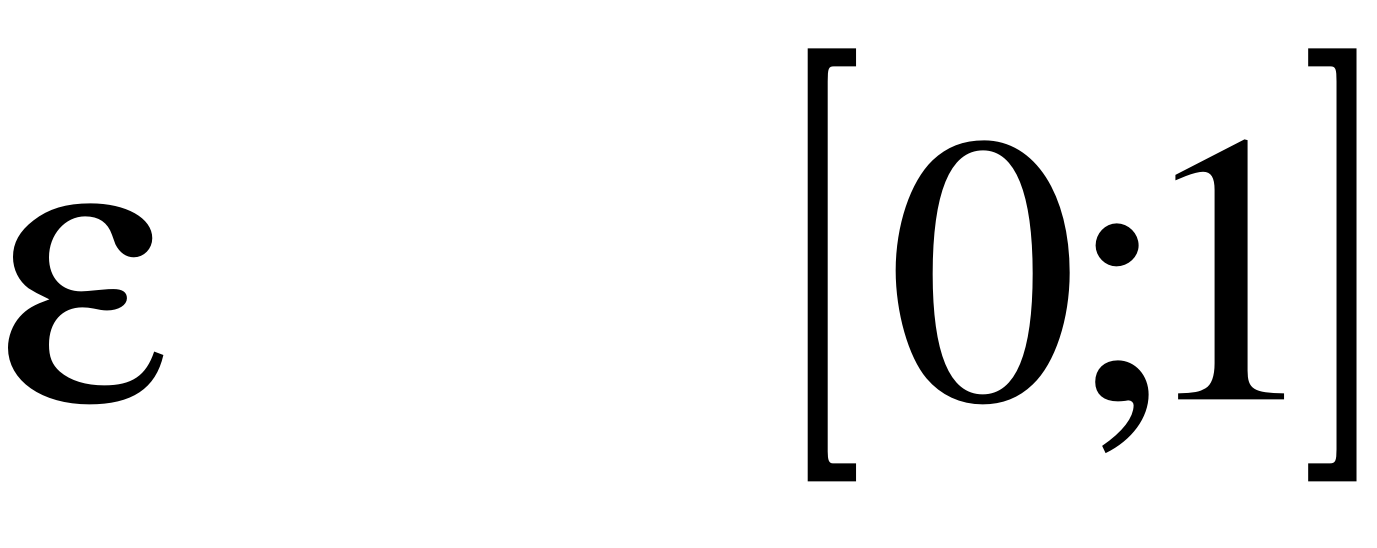

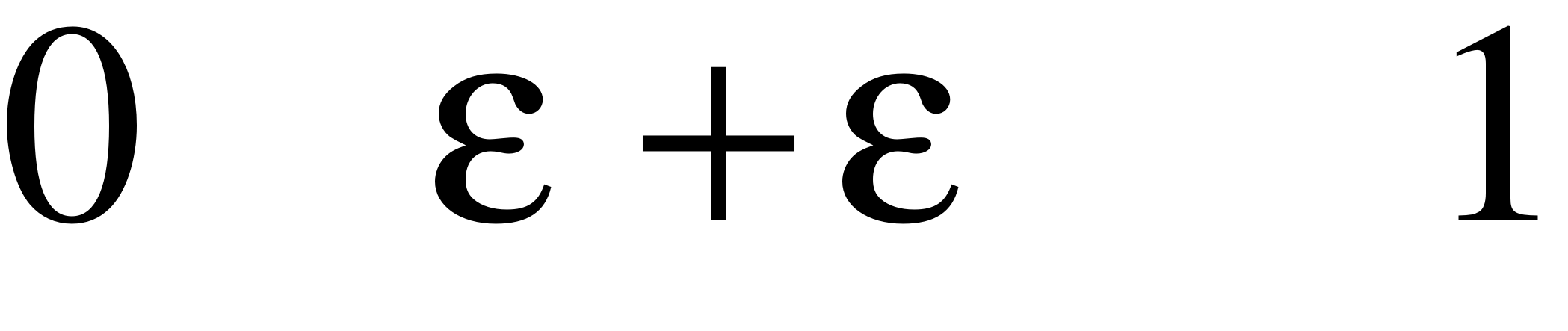
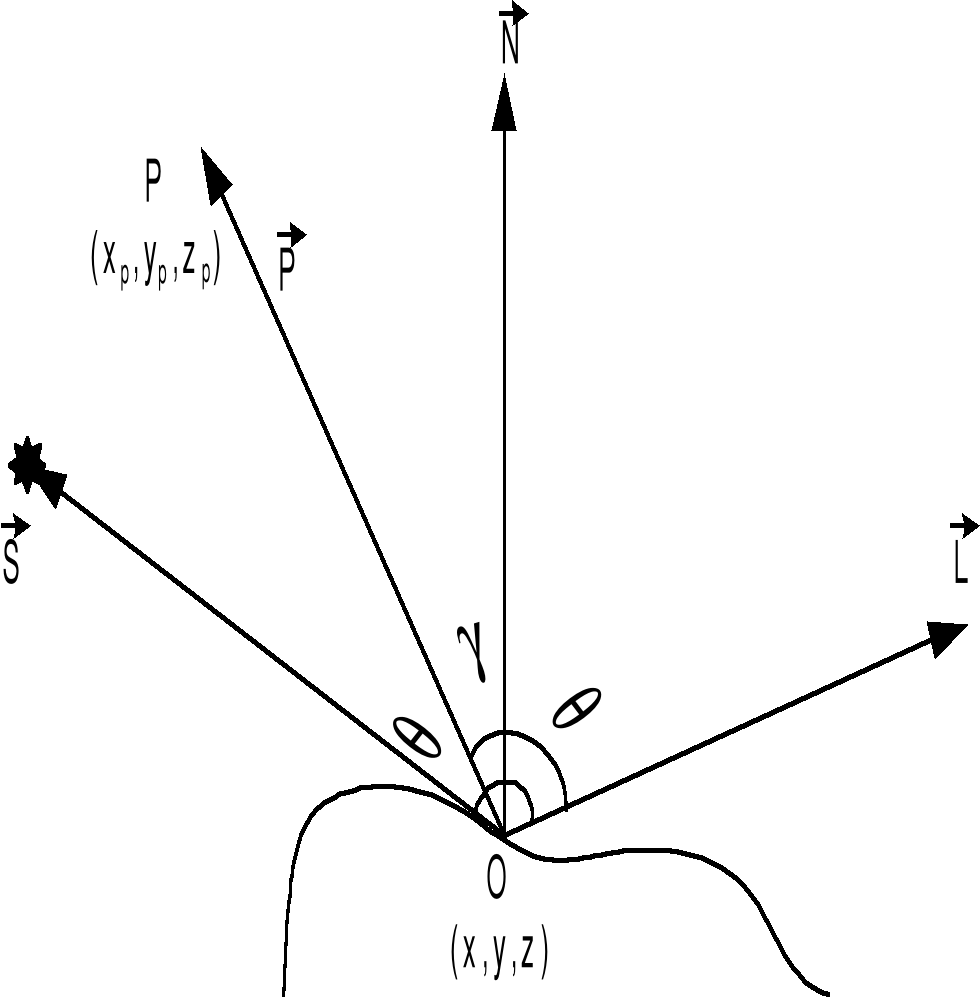
Рис. 5

Если угол g > 90° , то не надо учитывать зеркальную составляющую

Лунная модель

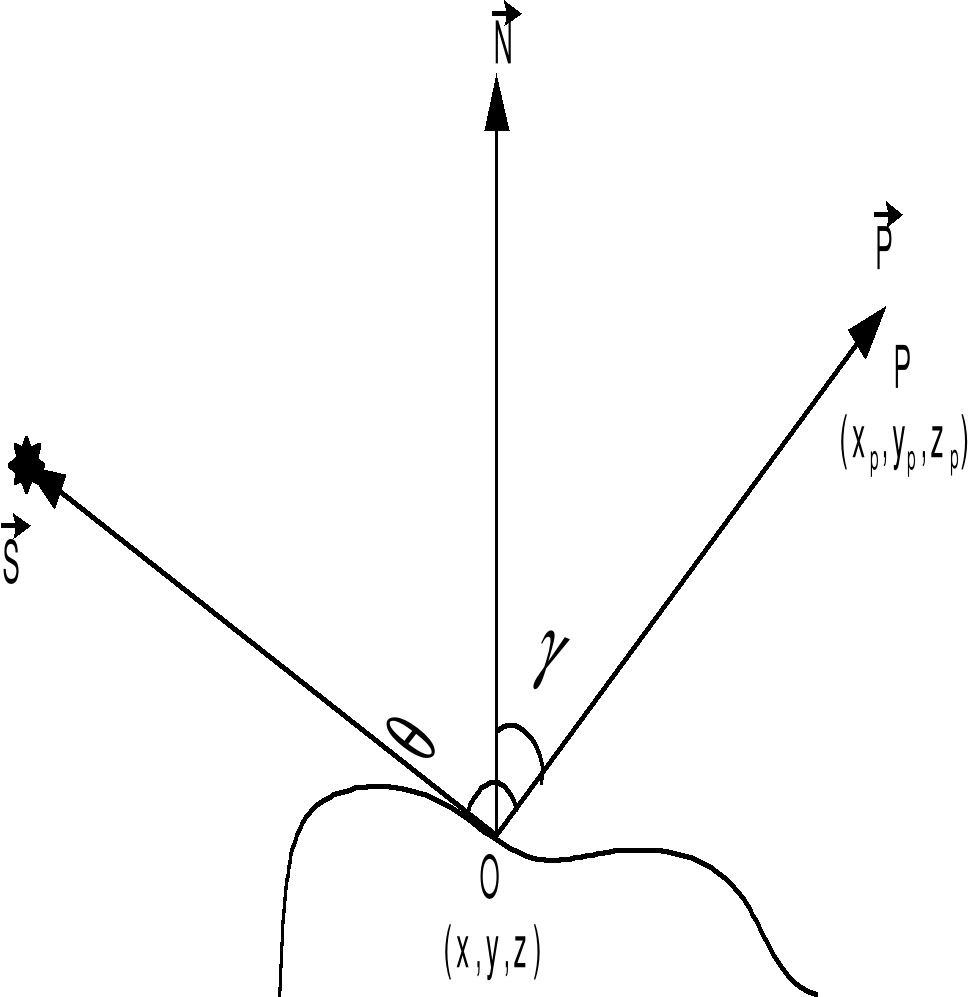
Рис. 6

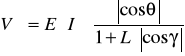– формула Гуро

VД – диффузная составляющая света. Если L = 0 , получается закон Ламберта. L >0.

По сравнению с методом Ламберта эта модель уменьшает яркость точек, на которые мы смотрим под углом 90°, и увеличивает яркость тех точек, на которые мы смотрим вскользь

Применение законов освещения при синтезе объекта изображения.

Объект с четко выраженными гранями.

Метод закраски – flat

Основная идея: каждая грань закрашивается одним цветом.

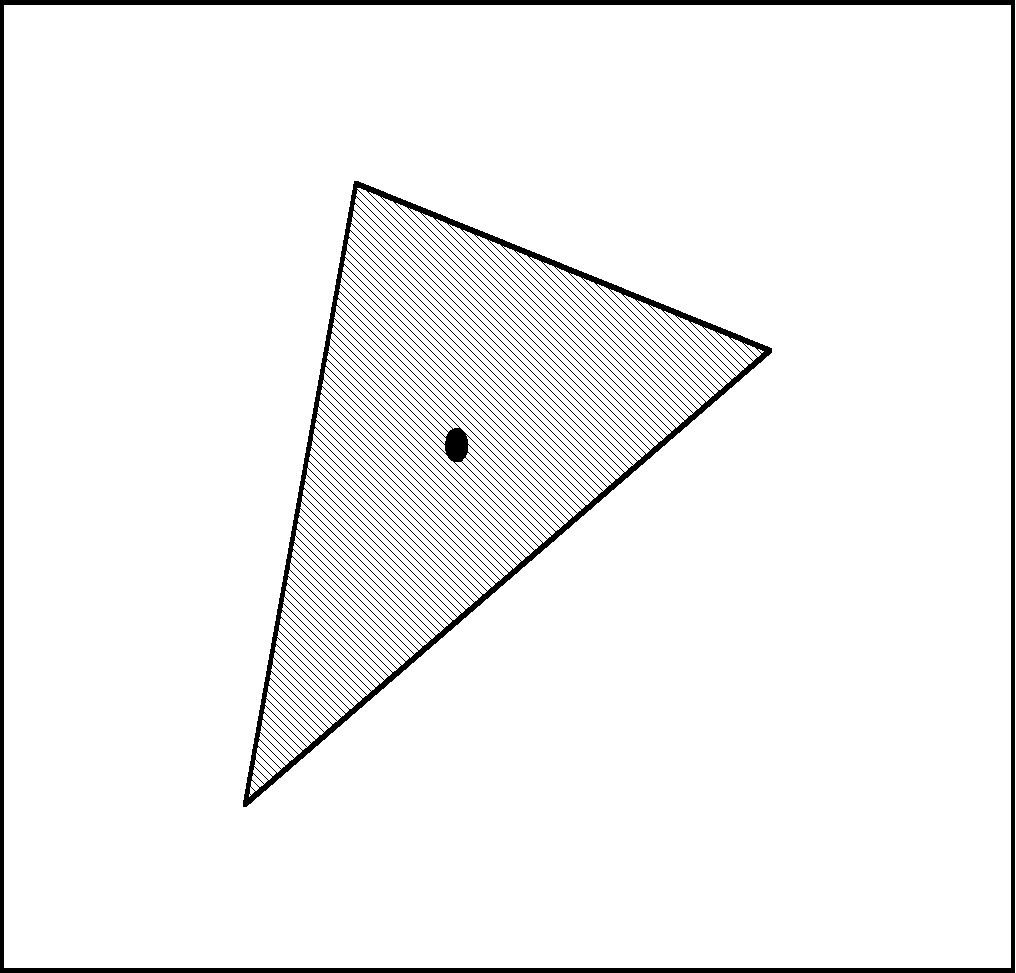
Рис. 7

Рассчитывается яркость в одной точке (например, в центре тяжести для выпуклых многоугольников) грани (по Ламберту) и производится заливка грани полученным цветом.

Метод закраски Гуро

Основная идея: заливка осуществляется с учетом линейной интерполяции яркости, вычисляется яркость только для вершин многоугольника.

Рис. 8

Недостаток метода то, что если источник света проецирутся в плоскость многоугольника, то, используя этот метод заливки, будет получен результат рис.8 (1), хотя должно быть рис.8 (2).

Закраска по Фонгу

Основная идея: для каждой точки изображения устанавливаются пространственные координаты, исходя из которых, считаем g и получаем яркость для точки.

Недостаток метода – большая сложность вычислений.

Моделирование освещения методом наложения текстуры.

Можно упростить вычисления, сведя метод Фонга к процедуре нанесения текстуры.

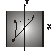
Рис. 9

Рис. 10

Основная идея: в памяти рассчитывается текстура рис. 9, затем заливка объектов осуществляется с использованием полученной текстуры.

· Рассчет вспомогательной текстуры.

Для каждой точки текстуры рассчитывается яркость по формуле

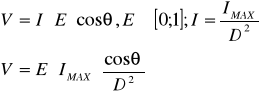
Пусть под яркость отведен 1 байт, т.е. 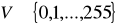– VMAX = 255.

Максимальная яркость будет в точке максимально приближенной к источнику света, т.е.

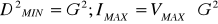
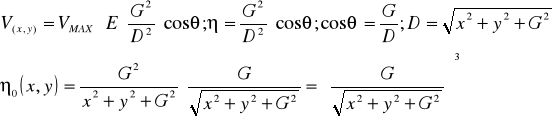
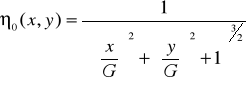
Если соответсявующим образом просматривать h, то получится яркость соответствующей точки в вспомогательной текстуре.

· Рассчет координатных точек для произвольного треугольника.

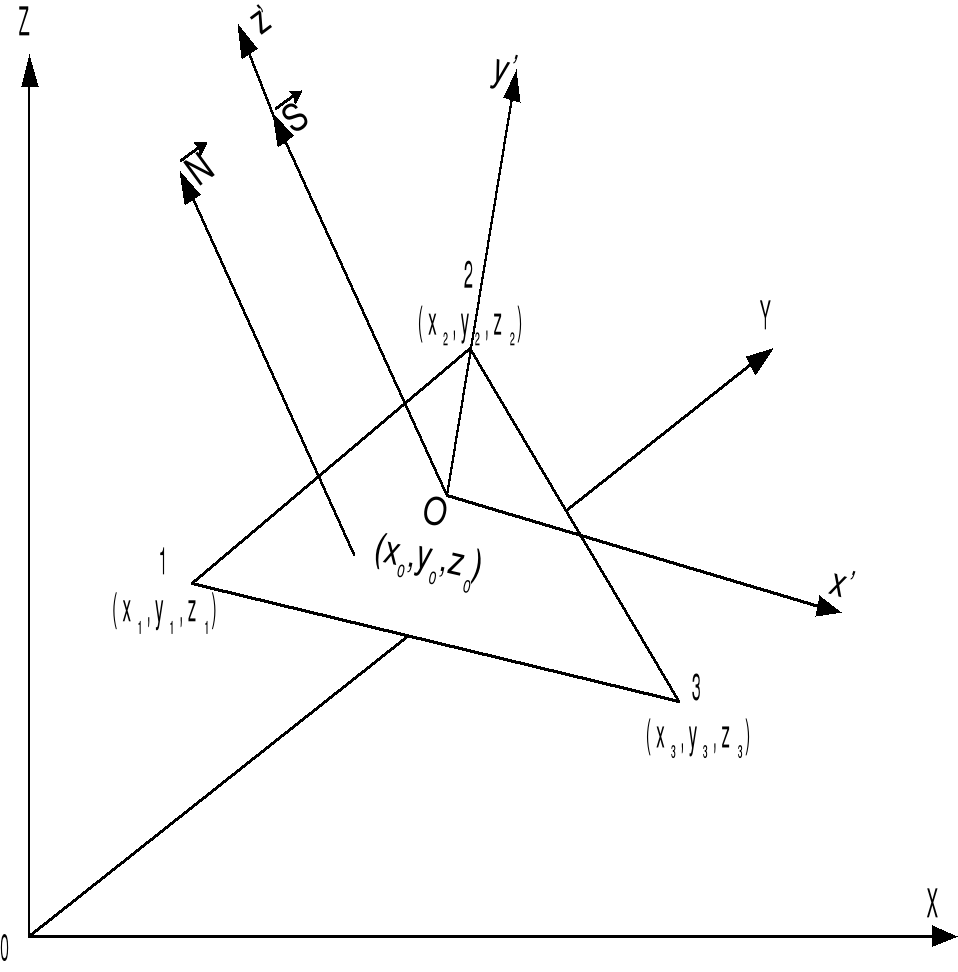
Рис. 11

В мировой системе координат задан произвольный треугольник рис. 11, необходимо провести его заливку с учетом освещенности.

Для этого строится система координат (x’,y’z’) с началом в точке О(x0,y0,z0), таким образом, что ось OZ проходит через источник света S и параллельна нормали 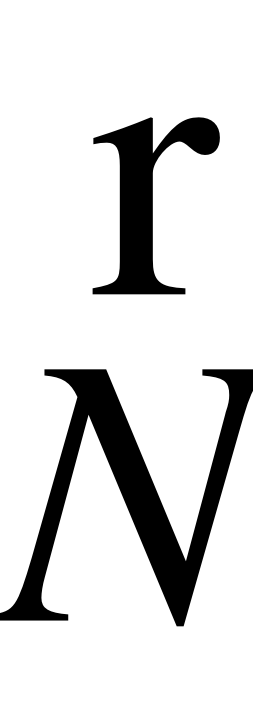, а OX и OY лежат в плоскости треугольника.

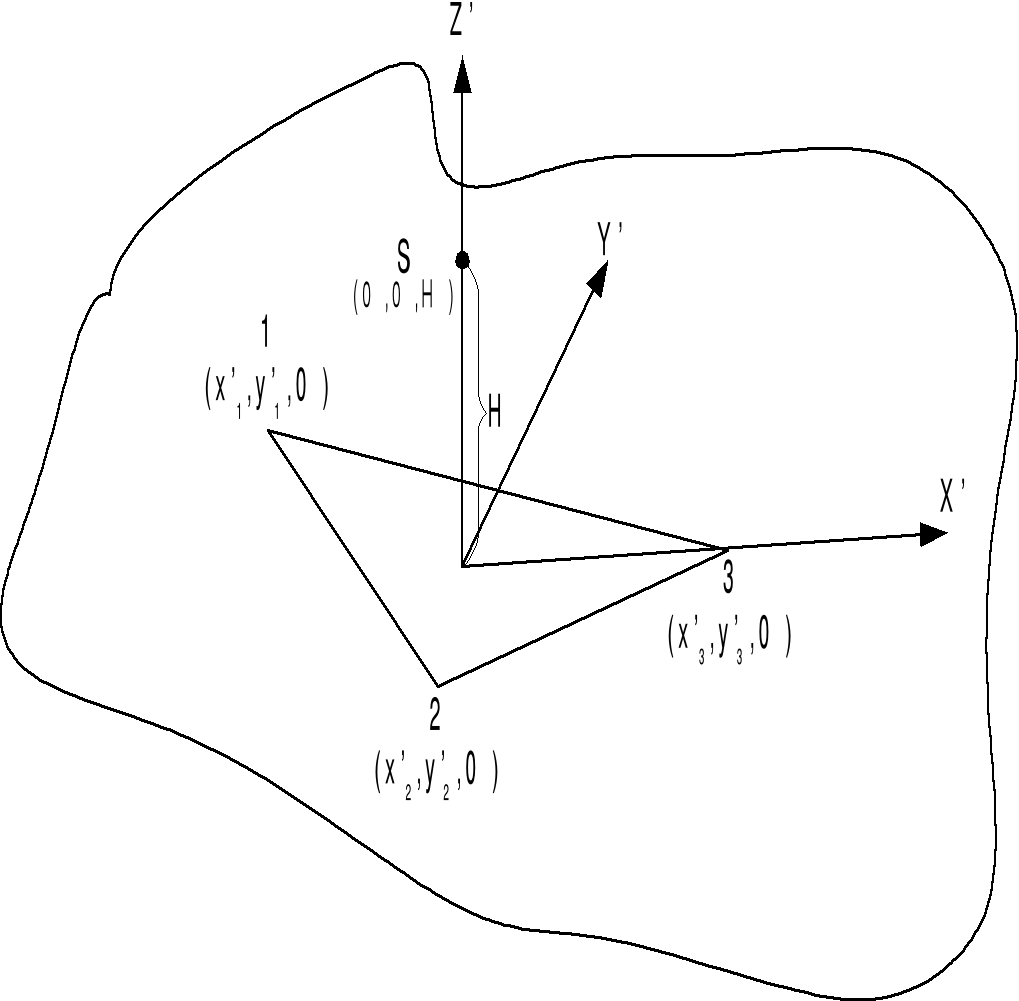
Рис. 12

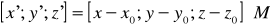, где M – матрица преобразования.

Найдем такую матрицу М, чтобы точки 1,2,3,S проецировались в точки с координатами которые озображены на рис. 12.

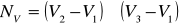– ненормированный вектор нормали

Пронормируем этот вектор: 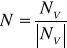; N(NX,NY,NZ)

Операясь на это выражение, вычисляем матрицу М:

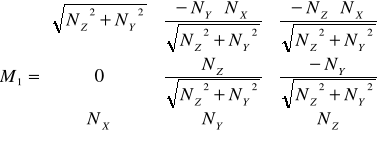
данная формула используется когда составляющая нормали NX = min;

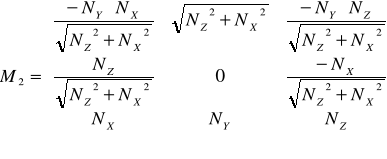
данная формула используется когда составляющая нормали NY = min;

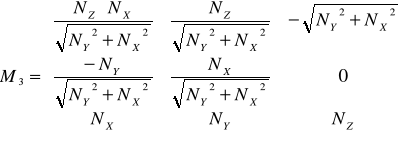
данная формула используется когда составляющая нормали NZ = min;

Для окончательного пересчета координат вершин треугольника будем пользоваться М умноженной на 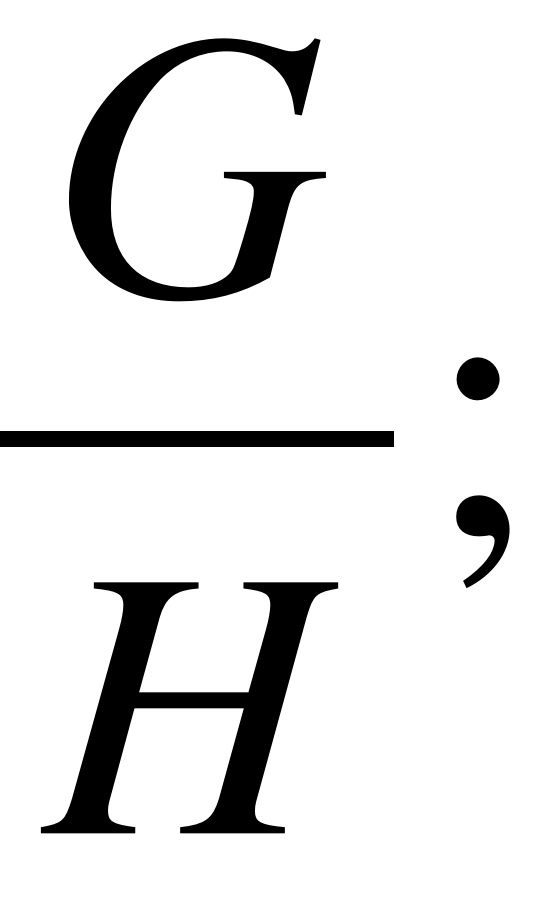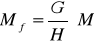; где М=М1, М2, М3.

Мf – матрица Фонга. Таким образом координаты в текстурном поле :

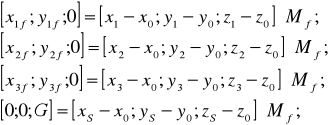
Последняя строка используется для контроля вычислений.

Схема закраски фигуры с учетом освещенности с использованием нанесения текстур.

1) Вычисляем h для каждой точки текстуры и записываем полученные результаты в таблицу, которую храним как текстурное поле.

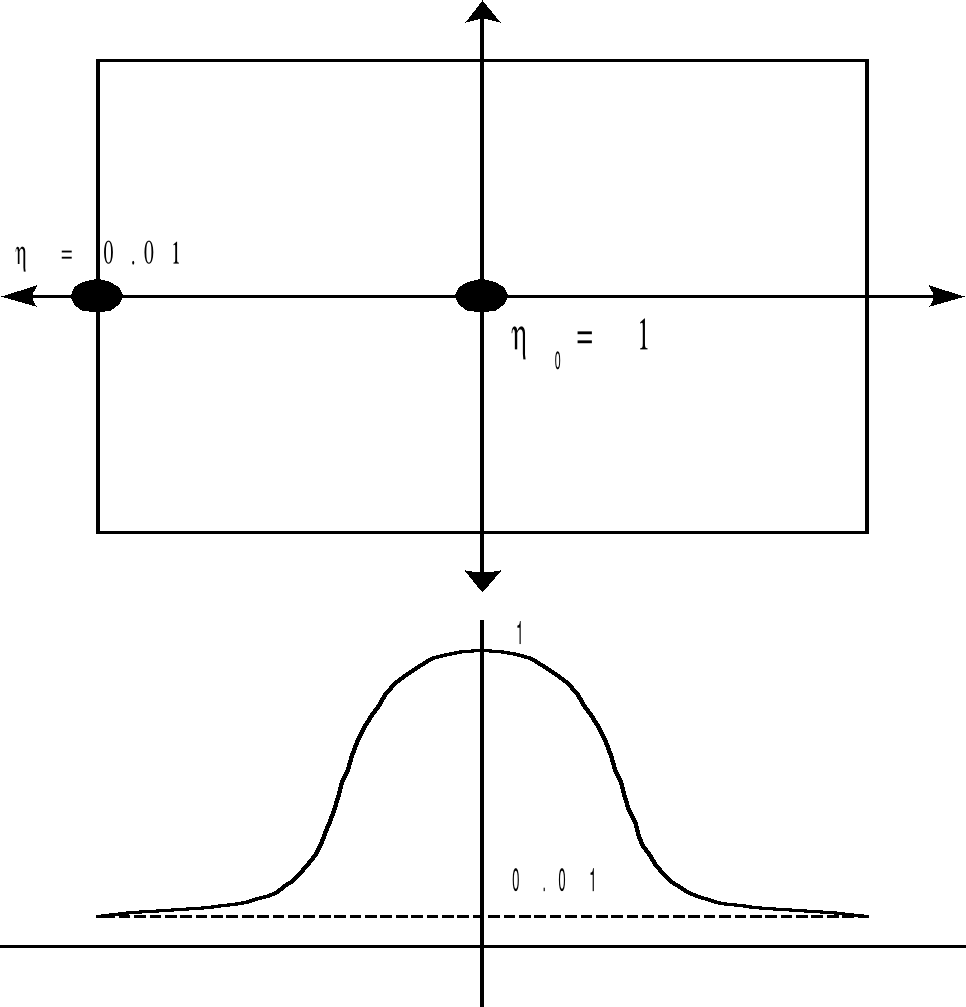
Рис. 14

На рис. 14 показан примерный диапазон и характер изменения h.

2) Высчитываем нормаль к поверхности треугольника

;

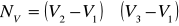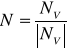
3) Пересчитываем координаты в текстурные, используя Мf

;

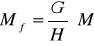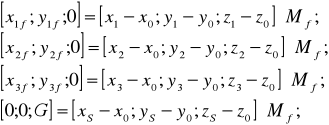
4) Рассчитываем яркость каждой точки.

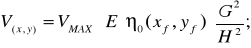
Если учитывать рассеянный свет, то 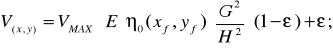, где e - доля рассеянного света.

8.2.2. Объект имеет гладкую форму.

Аналог алгоритма Гуро

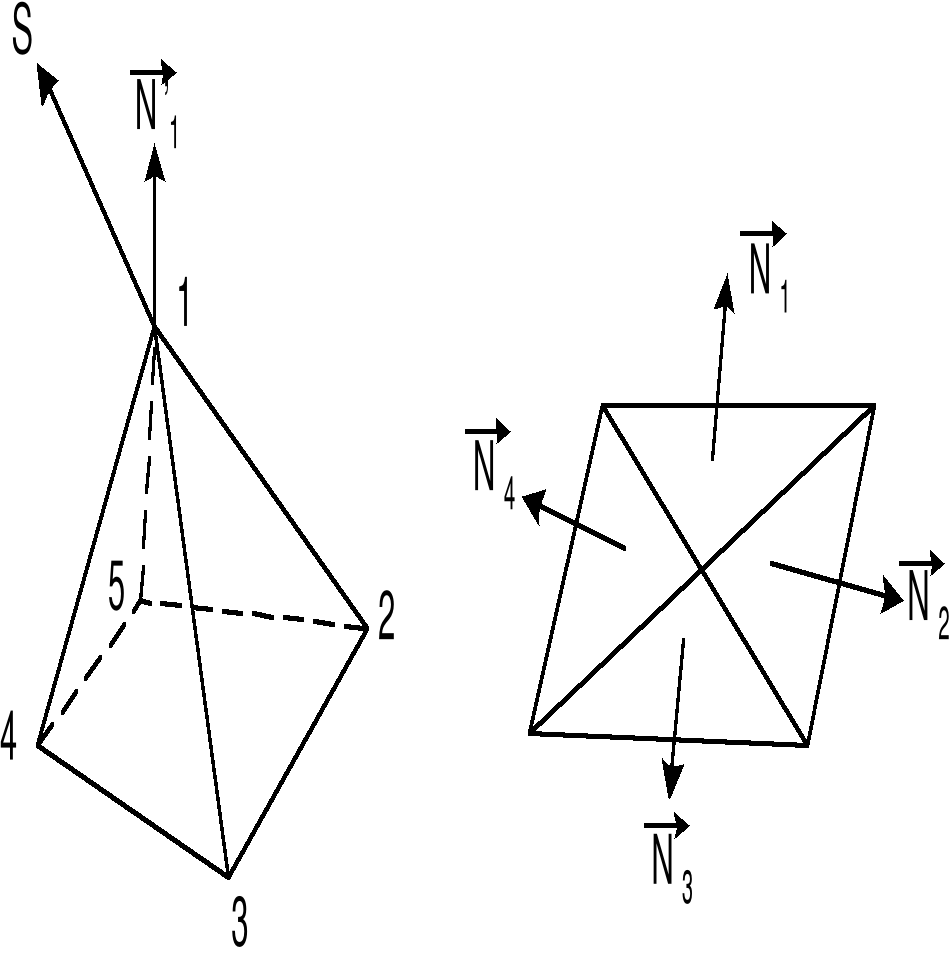
Рис. 15

Яркость рассчитывается в каждой вершине, а яркость на гранях и ребрах получается линейной интерполяцией. В качестве нормали при расчетах яркости в одной вершине используется средняя нормаль , где n – число прилегающих к этой вершине граней. – вектора площади, перпендикулярные соответсвующей грани и равные ее площади, таким образом учитывается то, что грани могут быть разного размера, а следовательно по-разному влиять на среднее значение нормали.

Рассчитанная таким методом яркость вершины используется для всех прилегающих к ней ребер, а следовательно со всех сторон вершины яркость одинакова и перепада яркости на ребрах не будет.

Аналог алгоритма Фонга

Основная идея: рассчитываются средние нормали, и производится интерполяция нормалей, т.е. линейная интерполяция по каждой координате (x,y,z).

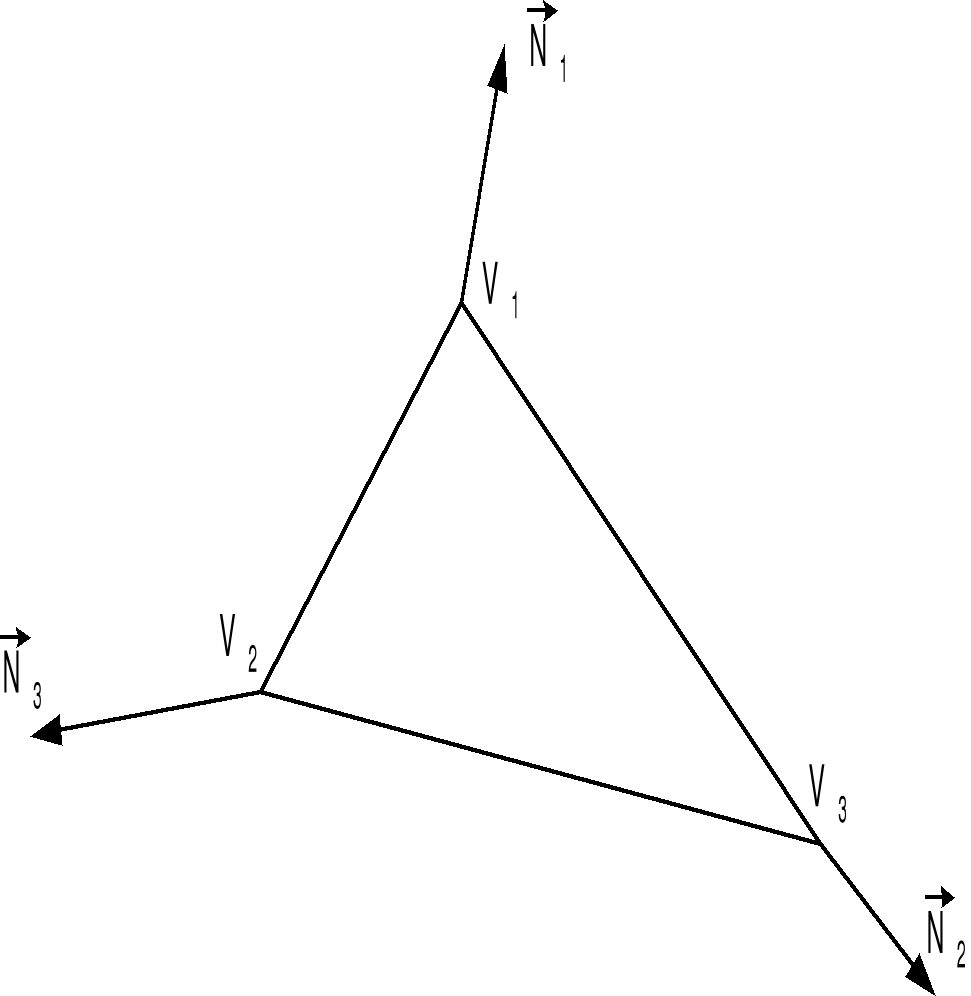
Рис. 16

Недостаток метода – если поверхность неровная, то возможны неточности рис.17

Рис.17

Трассировка лучей.

Всё что было рассмотрено ранее относится к проективным методам синтеза. Альтернативой им является трассировка лучей, так же как и проективные методы поддерживается проективно.

Суть: отслеживание луча.

Существуют:

1) Обратная трассировка луча (движение на встречу лучу);

2) Прямая трассировка луча (движение в противоположную сторону).

Обратная трассировка

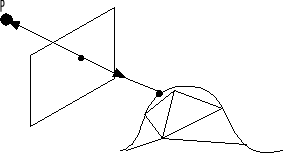
Надо найти точку пересечения луча с ближайшим многоугольником (с объектом трёхмерного изображения). Эта задача решается с помощью сортировки элементов пространственной сце-. ны.

Недостатки:

1) Для сложных сцен трассировка лучей не эффективена;

3) Струсктура вычислений сложнее, чем в проективных медодах.

Но метод трассировки лучей более эффективен, чем проективный метод для простой (гладкой) сцены, которая может быть описана математически, т. е.:

1) Решается система уравнений;

2) Находится точка пересечения;

3) Находится яркость.

Так же трассировка лучей эффективна для обработки диффузных поверхностей.