ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ И РАСПОЗНАВАНИЕ КРИВЫХ

Лекция 10

Тема. ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ И РАСПОЗНАВАНИЕ КРИВЫХ

Цель. Дать понятие о методах распознавания кривых

  1. Учебная. Разъяснить применение математической логики в диагностике состояний и использование методов распознавания для идентификации кривых.
  2. Развивающая. Развивать логическое мышление и естественное - научное мировоззрение.
  3. Воспитательная. Воспитывать интерес к научным достижениям и открытиям в отрасли телекоммуникации.

Межпредметные связи:

  • Обеспечивающие: информатика, математика, вычислительная техника и МП, системы программирования.
  • Обеспечиваемые: Стажерская практика

Методическое обеспечение и оборудование:

  1. Методическая разработка к занятию.
  2. Учебный план.
  3. Учебная программа
  4. Рабочая программа.
  5. Инструктаж по технике безопасности.

Технические средства обучения: персональный компьютер.

Обеспечение рабочих мест:

  • Рабочие тетради

Ход лекции.

  1. Организационный момент.
  2. Анализ и проверка домашней работы
  3. Ответьте на вопросы:
  4. На чем основаны метрические методы распознавания? Что используется в качестве изображения объекта?
  5. Дайте классификацию пространству признаков.
  6. Дайте объяснение алгоритму распознавания.
  7. В чем суть алгоритма распознавания при использовании метода минимального расстояния до множества?

План лекции

  1. ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ

1.1 Булевские функции

  1. Использование булевских функций для построения диагностических устройств

2 РАСПОЗНАВАНИЕ КРИВЫХ

2.1 Оценка неслучайных отклонений по контрольным уровням.

  1. ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ

Логические методы основаны на установлении логических связей между признаками и состояниями объектов, поэтому будут рассмотрены только простые (качественные) признаки, для которых возможны лишь два значения (например 0 и 1). Точно также и состояния технической системы (диагнозы) в рассматриваемых методах могут иметь только два значения (наличие и отсутствие). Два значения признака или состояния системы могут быть выражены любыми двумя символами («да» —«нет», «ложь» —«истина», 0—).

Переменные величины или функции, принимающие только два значения (0 и 1), называются логическими или булевскими. Исследованием таких переменных и функций занимается математическая логика, имеющая обширные приложения во многих технических проблемах (релейные системы, теория ЭВМ и автоматов и др.).

Детерминистское описание с помощью двоичных переменных, характерное для логических методов распознавания, является приближенной моделью реальной ситуации. Однако во многих задачах логические методы пригодны для начальных этапов распознавания. Весьма перспективны методы математической логики для второго направления технической диагностики —поиска и локализации неисправностей технических систем.

Основные понятия алгебры логики.

Логической величиной (или высказыванием) называется величина, которая может принимать только одно из двух значений: 0 или 1, «ложь» или «истина». Логические переменные обычно обозначаются заглавными буквами латинского алфавита.

Логической суммой двух логических переменных А и В (или дизъюнкцией) называют логическую величину С:

А\/В = С (1)

где V —знак логического сложения (дизъюнкции). Часто для логического сложения используется также знак + .

Величина С является истинной (С = 1), если истинно хотя бы одно из высказываний А и В или оба вместе. Таким образом, для дизъюнкции

1v1=1; 1+1=1;

v1=1; 0+1=1;

1v0=1 ; 1+0=1;

0v0=0; 0+0=0.

Логическое суммирование при словесном выражении соответствует союзу «или». Слово «или» может служить и обозначением операции дизъюнкции.

Логическим произведением двух логических величин А и В (или конъюнкцией) называют логическую величину С:

А/\В = С% (2)

где /\ —знак логического умножения (конъюнкции).

Для логического умножения используются и обычные знаки умножения x. Величина С является истинной только в том случае, когда истинными оказываются высказывания А и В. Таким образом, для конъюнкции

1/\ 1=1 x1=1

0 /\ 1=0 x1=0

1 /\ 0=0 x0=0

0 /\ 0=0 x0=0

Логическое произведение в словесном выражении соответствует союзу «и». Слово «и» может служить и обозначением операции конъюнкции.

В булевой алгебре часто используется операция отрицания высказывания А. Она обозначается А и читается «не A». Естественно, что истинность и ложность высказываний A и A противоположны.

Операции «и», «или», и «не» (конъюнкция, дизъюнкция, отрицание) позволяют составить различные комбинации высказываний, которые называются булевскими функциями и сами, разумеется, являются логическими величинами. Простейшие, наиболее употребительные булевские функции получили название операций импликации и эквивалентности. Импликация двух высказываний обозначается следующим образом:

А —> В, (14.5)

где —> —знак импликации (иногда используется знак 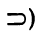). Соотношение (14.5) читается так: «A влечет В» или «если A, то В».

Импликация (следование) представляет собой операцию, результат которой С является логической величиной: (А —В) = С. (14.6)

Импликация может быть выражена с помощью двух основных операций в такой форме:

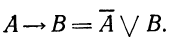(14.7)

Таким образом, импликация представляет собой простейшую булевскую функцию высказываний A и В. Если импликация является истинной, то при истинном А должно быть истинным В (А влечет В). Если А оказывается ложным, то при истинности импликации высказывание В может быть как истинным, так и ложным. Отметим, что из условия (14.5) не следует условие В —> A, т. е. высказывания А и В —неравноправны.

Рассмотрим еще эквивалентность (или тождественность) двух высказываний, обозначаемую так:

А = В, (14.8)

где = знак эквивалентности.

Условие (14.8) представляет собой логическую величину С:

(A = В) = С, (14.9)

которую можно выразить с помощью элементарных операций

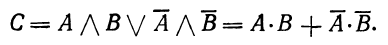(14.10)

Следовательно, если эквивалентность истинна (С = 1), то величины A и В обе или истинны, или ложны. Истинность операций приведена в табл. 4.

Таблица 4 Таблица истинности логических операций

А

B

А V В

А/\В

А -> В

A=B

0

0

0

0

1

1

1

0

1

0

0

0

0

1

1

0

1

0

1

1

1

1

1

1

Отметим еще некоторые простейшие булевские выражения, которые остаются истинными, независимо от истинности или ложности входящих в них высказываний. Например, С = А V A, С = (A V А) V В. Такие выражения называются тавтологиями.

1.1 Булевские функции. Булевской функцией называется логическая величина, значение которой зависит от других логических величин:

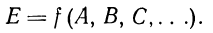(14.11)

В этом равенстве Е является булевской функцией логических переменных А, В, С, .... Как и для обычных функций, функциональная зависимость выражает последовательность операций, совершаемых над переменными. Примерами булевских функций могут служить выражения

F = AVB/\C, F = A/\B/\C. (14.12)

В дальнейшем рассматриваются булевские функции, включающие операции «или», «и» и «не». Во многих случаях для сокращения записи и наглядности используется операция импликации. Например, выражение

F = A\/B/\C\/D (14.13)

записывается в виде

F=(A-B)/\(C-D). . (14.14)

Правила абсорбции:

А + А = А А*А = А. (14.15)

Правила коммутативности:

А+Б = Б + А; А-В/\В-А. (14.16)

Правила ассоциативности:

(А + В) + С = А+ (В + С) = А+ В + С; (14.17)

(А*В)*С = А*(В*С) = А*В*С.

Правило дистрибутивности умножения относительно сложения
А*(В+С) = А*В + А*С. (14.19)

Правило дистрибутивности сложения относительно умножения
А + В*С = (А + В)*(А + С). (14.20)

Этого правила нет в обычной алгебре.

Правила отрицания (правила Моргана):

A*B = A + B (14.21)

А + В = А*В. (14.22)

Правила поглощения:

А*В + А*В = А; (A + B)*(A + В) = A;

А+А*В= А; А*(А+В) = A. (14.23)

Базис булевской функции и изображающие числа. Для задач диагностики целесообразно ввести некоторые понятия, связанные с булевскими функциями.

Базисом булевской функции будем называть совокупность всех возможных значений ее аргументов (область задания функции). Если булевская функция содержит п логических переменных, то базис состоит из 2п чисел (0 или 1). Записать базис можно разными способами, но условимся придерживаться правил, которые поясним примерами. Для функции трех аргументов (А, В, С) нормальный базис запишем в такой форме:

А 01 01 01 01

В 00 11 00 11 (14.24)

С 00 00 11 11.

Аргументы идут в порядке следования, в первой строке имеются перестановки чисел 0 и 1, во второй —перестановки пар чисел, в третьей —четверок чисел. Число одинаковых цифр в перестановке равно 2i-1, где i —номер строки. Каждую строку базиса можно рассматривать как двоичное число, которое называется изображающим числом аргумента и обозначается знаком). Каждый столбец базиса также представляет собой двоичное число, равное номеру столбца (от 0 до 7).

1.2 Использование булевских функций для построения диагностических устройств.

Диагностические устройства представляют собой приборы, моделирующие связи признаков и состояний. Они позволяют автоматически вводить двоичные признаки включением тумблеров и получать сведения о возможных состояниях системы, например, с помощью световых сигналов (загорания лампочек). Связь признаков и состояний систем выражается булевской функцией, которую будем называть булевской диагностической функцией.

Диагностические устройства можно рассматривать как реализацию условий истинности булевской диагностической функции.

Пусть имеются простые (двоичные) признаки kl9 k2, k3i ..., с помощью которых различаются состояния системы. Наличие признака обозначается числом 1, отсутствие признака числом 0. Таким образом,

1 —наличие признака; (14.26)

0—отсутствие признака.

Часто наличие или отсутствие признака kj будем обозначать следующим образом: наличие признака kj (kj = 1); отсутствие признака kj (kj = 0). Состояния системы обозначаются D1 D2 D3 ..., причем наличие состояния соответствует числу 1 и отсутствие числу 0:

1—наличие i-го состояния;
0 —отсутствие i-гo состояния.

Логические методы позволяют выявить состояния, не противоречащие имеющимся техническим сведениям о связях состояний и признаков. К числу логических методов распознавания могут быть отнесены методы теории графов, лингвистические и другие методы, которые здесь не рассматриваются.

  1. РАСПОЗНАВАНИЕ КРИВЫХ

Во многих случаях информация о состоянии системы (машины) содержится в виде записи значений диагностического параметра или его отклонений от нормального или первоначального уровня в различные моменты времени. Результаты представляются в виде непрерывных функций х (кривых) или совокупности дискретных значений 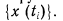. Принципиальной разницы между этими двумя видами информации нет и, ограничиваясь некоторой максимальной частотой периодической составляющей, можно указать шаг квантования, при котором за период наблюдения Т непрерывная и дискретная формы записи эквивалентны. В других случаях дискретное представление можно рассматривать как приближенное.

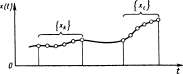
Наличие неисправности может проявиться в росте отдельных периодических составляющих в спектральном составе, в существенном изменении значений диагностического "параметра и т. п. Анализируя протекание кривой х (t), можно во многих случаях сделать важные заключения о техническом состоянии системы (машины). Установление соответствия между состоянием системы и протеканием отображающих функций х (t) будем называть распознаванием (идентификацией) кривых

Рис. 2. Обнаружение систематических отклонений по выборочным данным

Для технической диагностики представляет интерес решение двух основных вопросов.

  1. Являются ли наблюдаемые во время эксплуатации изменения кривой х (t) следствием случайных, несущественных изменений в системе или они вызваны более серьезными причинами.
  2. Если отличия в протекании кривой являются значительными, то с какими из возможных состояний системы они связаны.
    При непрерывном слежении за параметрами системы вторая задача решается после первой, при выборочном наблюдении или анализе указанные задачи независимы.

Основная идея методов распознавания кривых состоит в отображении бесконечного многообразия значений функции в конечномерное пространство признаков.

Различные методы распознавания отличаются выбором системы признаков и способами разделения состояний в пространстве признаков.

2.1 Оценка неслучайных отклонений по контрольным уровням.

В практических задачах для оценки неслучайных отклонений при непрерывной записи параметров часто используются заранее назначаемые контрольные уровни. В сущности, большинство сигнализирующих устройств диагностического назначения выдают сигналы о достижении определенного (опасного) уровня. Достижение предельного уровня при единичном выбросе еще не служит достаточно обоснованным свидетельством опасного состояния, так как возможны случайные помехи.

Часто для повышения достоверности оценки используется предупредительный уровень (отклонение 1на) и предельный уровень (отклонение 2). Например, при достижении параметром х (t) отклонения 1 сверх нормального уровня х0 загорается сигнальная лампочка, после превышения х0 2 происходит автоматическое отключение системы. Уровни 1 и 2 определяются на основании специальных испытаний и анализа последствий дефектов. Если учесть случайную нестабильность параметра, то следует принимать

Ограничение по контрольным уровням является более грубым, чем ограничение по методу средних, так как часто параметр не достигает предельного уровня, но его отклонения свидетельствуют о возникновении неисправности.

Оценка текущего значения параметра. В практических случаях возникает задача оценки текущего значения измеряемого параметра х (t). Требуется определить, является ли значение х (tn) одним из возможных, случайных отклонений или его нельзя согласовать с предыдущим течением процесса.

В связи с этим для эффективной оценки текущего значения х (t) необходимо знать не менее десяти его прежних значений.

Если условие нарушено, то значение х (t) для принятых степени значимости и доверительной вероятности не может быть согласовано с предыдущими значениями и свидетельствует о воздействии на процесс источника возмущения.

Общая задача распознавания кривых, метод признаков.

Метод признаков предназначен для решения более общей задачи распознавания —установления связи между поведением кривой и состоянием системы.

Пусть имеется некоторое число состояний системы Dt и предполагается, что каждому состоянию соответствует определенный класс кривых xt(t). Предъявляется для распознавания кривая х (t) за период времени Т и требуется отнести ее к одному из классов. Для того чтобы свести эту задачу к изученной ранее проблеме распознавания, необходимо охарактеризовать все рассматриваемые кривые в единой системе признаков, т. е. отобразить кривые в конечно-мерном пространстве признаков. Формирование пространства признаков представляет собой наиболее специфическую часть проблемы распознавания кривых.

Формирование признаков с помощью разложения в ряд по ортогональным функциям. В качестве признаков кривой х (t) на участке t0 < t < t1 можно принять коэффициенты разложения функции в ряд Фурье.

Формирование признаков по методу элементов. В качестве признаков могут быть использованы характерные элементы кривой х (t): точки минимума, максимума и др. Значительный опыт распознавания кривых по методу элементов имеется в медицинской диагностике.

В задачах технической диагностики в качестве элементов часто используется значение амплитуды колебаний с некоторой частотой. В этом случае проводится предварительный анализ спектра частот колебаний, возникающих при различных неисправностях и отказах..

Распознавание кривых по комплексу признаков. Если кривая на некотором участке представлена комплексом диагностических параметров (признаков) xl x2, ..., хп то процесс распознавания осуществляется статистическими методами, методами разделения в пространстве признаков, метрическими и др. Задача распознавания облегчается тем, что обычно признаки xt являются физически однородными параметрами (параметрами с одинаковой размерностью).

Сглаживание кривых. Во многих случаях кривая изменения диагностического параметра существенно искажается за счет неизбежных ошибок измерений. Это свойственно параметрам, записываемым вручную по показаниям стрелочных приборов или при недостаточной точности измерений и т. п. В таких случаях целесообразно проводить анализ предварительно сглаженных кривых. Существуют два основных метода сглаживания: метод наименьших квадратов и метод преобразования.

Часто применяется метод скользящего среднего. По этому методу величина xf представляет собой среднее нескольких значений, непосредственно примыкающих к измерению.

Практически осреднение проводится не более чем для 10 соседних значений параметра.

Можно заметить, что весовые коэффициенты, убывают по закону геометрической прогрессии со знаменателем q = 1 —а. Однако запоминания предыдущих значений параметра в расчетной процедуре не требуется, достаточно хранить только предыдущее сглаженное значение, что упрощает машинную реализацию алгоритма.

Выбор метода сглаживания и весовых коэффициентов определяется особенностями поведения кривой х (t), характером случайных отклонений, задачами диагностики и осуществляется на основании практического опыта. Метод сглаживания должен исключить случайные погрешности, но сохранить общую тенденцию изменения параметра.

Домашнее задание: § конспект.

Закрепление материала:

Ответьте на вопросы:

  1. Дайте определения и запишите следующие правила:
  • Правила абсорбции:
  • Правила ассоциативности:
  • Правила коммутативности:
  • Правило дистрибутивности умножения
  • Правило дистрибутивности сложения
  • Правила отрицания
  • Правила поглощения:
  1. Что представляет собой операций импликации? Приведите пример.
  2. Что называют Базисом булевской функции?
  3. Решение каких вопросов представляет интерес для технической диагностики? В чем состоит основная идея методов?
  4. По каким методам происходит формирование признаков?
  5. Как осуществляется распознавание кривых по комплексу признаков? За счет чего существенно искажается кривая изменения диагностического параметра? Какие основные методы сглаживании вы знаете?

Литература:

  1. Амренов С. А. «Методы контроля и диагностики систем и сетей связи» КОНСПЕКТ ЛЕКЦИЙ -: Астана, Казахский государственный агротехнический университет, 2005 г.
  2. И.Г. Бакланов Тестирование и диагностика систем связи. - М.: Эко-Трендз, 2001.
  3. Биргер И. А. Техническая диагностика.—М.: «Машиностроение», 1978.—,с, ил.
  4. АРИПОВ М.Н , ДЖУРАЕВ Р.Х., ДЖАББАРОВ Ш.Ю. «ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ЦИФРОВЫХ СИСТЕМ» -Ташкент, ТЭИС, 2005
  5. Платонов Ю. М., Уткин Ю. Г. Диагностика, ремонт и профилактика персональных компьютеров. -М.: Горячая линия - Телеком, 2003.-312 с: ил.
  6. М.Е.Бушуева, В.В.Беляков Диагностика сложных технических систем Труды 1-го совещания по проекту НАТО SfP-973799 Semiconductors. Нижний Новгород, 2001
  7. Малышенко Ю.В. ТЕХНИЧЕСКАЯ ДИАГНОСТИКА часть I конспект лекций
  8. Платонов Ю. М., Уткин Ю. Г.Диагностика зависания и неисправностей компьютера/Серия «Техномир». Ростов-на-Дону: «Феникс», 2001. —с.

ЛОГИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ И РАСПОЗНАВАНИЕ КРИВЫХ