Диагностическая ценность признаков

Лекция 16

Тема. Диагностическая ценность признаков

Цель. Дать понятие о диагностической ценности признаков.

Учебная. Разъяснить ценности признаков при диагностике.

Развивающая. Развивать логическое мышление и естественное - научное мировоззрение.

Воспитательная. Воспитывать интерес к научным достижениям и открытиям в отрасли телекоммуникации.

Межпредметные связи:

Обеспечивающие: информатика, математика, вычислительная техника и МП, системы программирования.

Обеспечиваемые: Стажерская практика

Методическое обеспечение и оборудование:

Методическая разработка к занятию.

Учебный план.

Учебная программа

Рабочая программа.

Инструктаж по технике безопасности.

Технические средства обучения: персональный компьютер.

Обеспечение рабочих мест:

Рабочие тетради

Ход лекции.

Организационный момент.

Анализ и проверка домашней работы

Ответьте на вопросы:

Что такое энтропия?

Каие требования задал Клод Шенон к измерению информации ?

Как связаны энтропия и пропускная способность канала?

Приведите математические свойства энтропии.

Что такое эффективность исходного алфавита?

Что называется условной энтропией первого порядка ?

Для чего предназначена взаимная энтропия или энтропия объединения?

Чему равна энтропия сложной системы ?

Что такое содержательный подход к измеению?

Приведите формулу Хартли.дайте ей пояснение.

Приведите формулу Хартли.

На чем основан основан алфавитный подход, что такое мощность алфавита ?

Что такое информация по  Шеннону? 

Что такое количество информации , мера измерения?

Дайте определение информационному объему сообщения, какие различают при этом подходы?

Какие меры информации выделяют в рамках структурного подхода к измерению информации?

Что определяет геометрическая мера измерения информации?

Что определяет комбинаторная мера измерения информации?

Что определяет аддитивная мера измерения информации?

От чего зависит количество информации в сообщении?

На чем основан объемный способ передачи последовательности знаков, сигналов?

Что в теории информации  называют количеством информации?

Какие подходы к измерению информации вам известны?

Какова основная единица измерения информации?

Сколько байт содержит 1 Кб информации?

Приведите формулу подсчета количества информации при уменьшении неопределенности знания.

Как подсчитать количество информации, передаваемое в символьном сообщении?

План лекции

1. Простые и сложные признаки и их диагностические веса
2. Диагностические веса признаков.
3. Связь диагностических весов реализаций простого признака.
4. Условный и независимый диагностические веса.
5. Диагностический вес реализации комплекса признаков.
6. Диагностическая ценность обследования
7. Выбор величины диагностических интервалов. Диагностическая ценность одновременного обследования по комплексу признаков.
8. Построение оптимального диагностического процесса Необходимый объем информации.Условия оптимальности.

ДИАГНОСТИЧЕСКАЯ ЦЕННОСТЬ ПРИЗНАКОВ

Вводные замечания. В технической диагностике очень важное значение имеет описание объекта в системе признаков, обладающих большой диагностической ценностью. Использование неинформативных признаков не только оказывается бесполезным, но и снижает эффективность самого процесса диагностики, создавая помехи при распознавании.

Количественное определение диагностической ценности признаков и комплексов признаков может быть проведено на основе теории информации. Признак определяется информацией, которая вносится признаком в систему состояний.

Простые и сложные признаки и их диагностические веса.

Простые и сложные признаки. Пусть имеется система Dn которая находится в одном из п возможных состояний Di (i = 1, 2, . . ., п). Условимся теперь называть эту систему «системой диагнозов», а каждое из состояний — диагнозом. В большинстве случаев непрерывные различные состояния системы представляются вовокупностью эталонов (диагнозов), причем выбор числа диагнозов часто определяется задачами исследования. Распознавание состояний системы D осуществляется путем наблюдения за другой, связанной с ней системой, — системой признаков.

Будем называть простым признаком результат обследования, который может быть выражен одним из двух символов или двоичным числом (например, 1 и 0; «да» и «нет»; + и — ).

С точки зрения теории информации простой признак можно рассматрирать как систему, имеющую одно из двух возможных состояний. Если kj — простой признак, то два его состояния будем обозначать: kj — наличие признака; kj — отсутствие признака. Простой признак может означать наличие или отсутствие измеряемого параметра в определенном интервале, он может иметь и качественный характер (например, положительный или отрицательный результат испытания и т. п.).

Для целей диагностики область возможных значений измеряемого параметра часто разбивается на интервалы и характерным является наличие параметра в данном интервале. В связи с этим результат количественного обследования может рассматриваться как признак, принимающий несколько возможных состояний.

Условимся называть сложным признаком (разряда т) результат наблюдения (обследования), который может быть выражен одним из т символов. Если, как обычно, в качестве символов избрать цифры, то сложный признак (разряда т) может быть выражен m-разрядным числом (например, сложный признак 8-го разряда выражается восьмиричным числом). Сложный признак может быть связан и с обследованием качественного характера, если оценка содержит несколько градаций [например, шум (увеличенный, нормальный, слабый) — трехразрядный признак]. Разряды признака часто будем называть диагностическими интервалами.

Разберем некоторые признаки.

Одноразрядный признак (т = 1) имеет только одно возможное состояние. Такой признак не несет какой-либо диагностической информации и его следует исключить из рассмотрения.

Двухразрядный признак (т = 2) обладает двумя возможными состояниями. Состояния двухразрядного признака kj можно обозначить kj1 и kj2. Пусть, например, признак kj относится к измерению параметра х, для которого установлено два диагностических интервала: х < 10 и х > 10. Тогда kj1 соответствует х 10, a kj2 обозначает х > 10.

Эти состояния альтернативны, так как реализуется только одно из них. Очевидно, что двухразрядный признак может быть заменен простым признаком kj если положить kj1 = kj и kj2 = kj. Этот простой признак можно сформулировать так: пониженное значение параметра х.

Трехразрядный признак (т = 3) имеет три возможные значения: kjl kj2 kj3. Пусть, например, для параметра x приняты три диагностических интервала: <5; 5—15; >15. Тогда для гфизнака kj, характеризующего этот параметр, возможны три значения:

х5 5<x<15 x15

т-разрядный признак k. имеет т возможных состояний: ki

Диагностические веса признаков.

Если в результате обследования выявлено, что признак kj имеет для данного объекта значение kjS то это значение будем называть реализацией признака kj. Обозначая ее k*j, будем иметь k*j = kjs.

В качестве диагностического веса реализации признака kj для диагноза Di примем

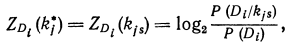(19.1)

где P (Di/kjS) — вероятность диагноза Di при условии, что признак kj получил значение kjs; Р (Di) — априорная вероятность диагноза.

Величина ZD. (kJS) называетcя величиной ценностью информации.

Таблица 9 Вероятности появления перегрузок, %

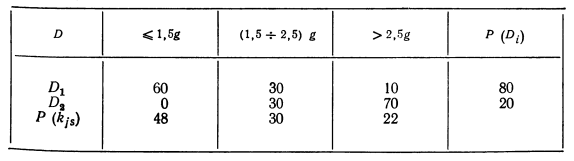
Из таблицы следует, например, что 10% исправных двигателей имеют перегрузку свыше 2,5 g.

На основании статистических данных 80% объектов имеют исправное состояние (для рассматриваемого ресурса) и 20% — неисправное. Величина перегрузки составляет признак kj имеющий три интервала. Например, Р (kj3) = Р (D1) X Р (kj3/D1 + Р (D2) Р (kj3/D2) = 0,8*0,1 + 0,2*0,7 = 0,22.

Диагностические веса интервалов признака будут такими: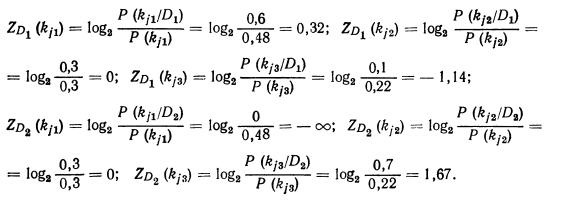

Отметим, что диагностический вес второго интервала равен нулю. Это ясно из физических соображений: из условия, что вибрационная перегрузка находится в пределах от 1,5 до 2,5g, нельзя сделать вывод о состоянии объекта.

Диагностический вес первого интервала для неисправного состояния равен —оо, что отрицает (по статистическим данным) возможность неисправного состояния.

Связь диагностических весов реализаций простого признака.

Простой признак kf может иметь две реализации: kj1= kj,kj2 = kj. В связи с этим можно говорить о наличии или отсутствии признака kj. Диагностический вес наличия признака kj для диагноза Dt

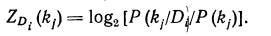(19.3)

Диагностический вес отсутствия признака
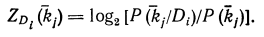(19.4)

Так как существуют очевидные соотношения
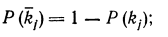(19.5)

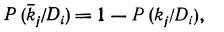(19.6)

то

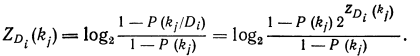(19.7)

Из формулы (19.7) вытекает, что 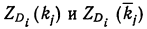всегда имеют разные знаки.

Отметим, что если признак k является случайным для данного диагноза 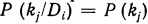, то оба диагностических веса равны нулю.

Условный и независимый диагностические веса.

Равенства (19.1) и (19.2) определяют независимый диагностический вес данной реализации признака для диагноза D. Он характерен для ситуации, в которой обследование по признаку kf проводится первым или когда результаты обследования по другим признакам еще неизвестны (например, при одновременном обследовании по нескольким признакам). Он также характерен для случая, когда вероятность появления данной реализации признака не зависит от результатов предыдущих обследований.

Однако известно, что диагностическое значение реализации признака во многих случаях зависит от того, какие реализации признаков получились в предыдущих обследованиях. Бывает, что сам по себе признак не имеет существенного значения, но его появление после некоторого другого позволяет однозначно поставить диагноз (установить состояние системы).

Пусть проводится обследование сначала по признаку k1 а затем по признакуk2.При обследовании объекта по признаку кг была получена реализация kls, и требуется определить диагностический вес реализации k2p признака k2 для диагноза Д. В соответствии с определением диагностического веса

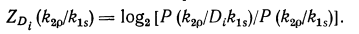(19.8)

Формула (19.8) определяет условный диагностический вес реализации признака.

Независимый диагностический вес этой реализации

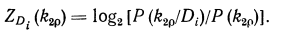(19.9)

Если признаки k1 b k2 являются независимыми для всей совокупности объектов с различными диагнозами

и условно независимыми для объектов с диагнозом Dt то условный и независимый диагностические веса реализации совпадают.

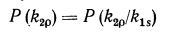
Диагностический вес реализации комплекса признаков.

Рассмотрим диагностический вес реализаций комплекса признаков K, состоящего из признака k1 с реализациями kls и признака K2 с реализациями k2р. Возможны два варианта проведения обследования по комплексу признаков: последовательный и параллельный.

При последовательном (поэтапном) обследовании сначала по признаку K1и затем по признаку K2 получим, что диагностические веса совпадают.

Диагностический вес реализации комплекса признаков не зависит от порядка проведения обследования.

Отметим, что понятие диагностического веса реализации признака применимо только по отношению к данному диагнозу, как степень его подтверждения или отрицания. Усреднение диагностического веса по всем реализациям признака и по всем диагнозам приводит к понятию информативной или диагностической ценности обследования.

Диагностическая ценность обследования

Частная диагностическая ценность обследования. Диагностический вес той или иной реализации признака еще не дает представления о диагностической ценности обследования по данному признаку. Например, при обследовании по простому признаку может оказаться, что его наличие не имеет диагностического веса, тогда как его отсутствие чрезвычайно важно для установления диагноза.

Условимся считать диагностической ценностью обследования по признаку kj для диагноза Dt величину информации, вносимую всеми реализациями признака kj в установление диагноза D. Для m-разрядного признака

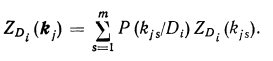(20.1)

Диагностическая ценность обследования учитывает все возможные реализации признака и представляет собой математическое ожидание величины информации, вносимой отдельными реализациями. Так как величина ZD (kj) относится только к одному диагнозу D то будем называть ее частной диагностической ценностью обследования по признаку kj.

Следует также отметить, что Zd (kj) определяет независимую диагностическую ценность обследования. Она характерна для случая, когда обследование проводится первым или когда результаты других обследований неизвестны. Величина ZD. (kj) может быть записана в трех эквивалентных формах:

Если признак kj является случайным для диагноза D то обследование по такому признаку не имеет диагностической ценности(ZDi(kf)=0).

Наибольшую диагностическую ценность имеют обследования по признакам, которые часто встречаются при данном диагнозе, а вообще редко и, наоборот, по признакам, встречающимся при данном диагнозе редко, а вообще — часто. При совпадении Р (kj/Dj) и Р (kj) обследование не имеет никакой диагностической ценности. Эти выводы совпадают с интуитивными правилами, используемыми на практике, но теперь эти правила получают точную количественную оценку.

Диагностическая ценность обследования вычисляется в единицах информации (двоичных единицах или битах) и не может быть отрицательной величиной. Последнее понятно из логических соображений: информация, полученная при обследовании, не может «ухудшить» процесс распознавания действительного состояния.

Выбор величины диагностических интервалов.

Величина ZDi (kj) может быть использована не только для оценки эффективности обследования, но и для целесообразного выбора величины диагностических интервалов (числа разрядов). Очевидно, что для упрощения анализа удобно уменьшать число диагностических интервалов, однако это может привести к уменьшению диагностической ценности обследования.

С увеличением числа диагностических интервалов диагностическая ценность признака возрастает или остается прежней, но анализ результатов становится более трудоемким. Следует иметь в виду, что увеличение числа диагностических интервалов часто требует привлечения дополнительного статистического материала для получения необходимой достоверности значения вероятностей интервалов.

Общая диагностическая ценность обследования. Известно, что обследование, обладающее небольшой диагностической ценностью для одного диагноза, может иметь значительную ценность для другого.

Диагностическая ценность одновременного обследования по комплексу признаков.

Диагностическая ценность обследования по комплексу признаков для всей системы диагнозов измеряется количеством информации, вносимой системами к1 и к2 в систему D:

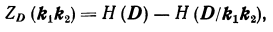(21.1)

где H (D) — априорная энтропия системы диагнозов; Н (D/k1k2) — ожидаемая энтропия системы диагнозов после обследования по признакам k1 и k2.

Построение оптимального диагностического процесса

Необходимый объем информации. В задачах диагностики чрезвычайно существенным оказывается выбор наиболее информативных признаков для описания объекта. Во многих случаях это связано с трудностью получения самой информации (число датчиков, характеризующих рабочий процесс машины, по необходимости весьма ограничено). В других случаях имеют значение время и стоимость диагностического обследования и т. п.

С теоретической точки зрения процесс диагностического обследования можно представить следующим образом. Имеется система, которая может находиться с некоторой вероятностью в одном из состояний, заранее неизвестном. Если априорные вероятности состояний Р (D) могут быть получены из статистических данных, то энтропия системы

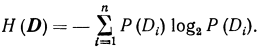(23.1)

В результате полного диагностического обследования по комплексу признаков К состояние системы становится известным (например, выясняется, что система находится в состоянии D1 тогда Р (D1) = 1, Р (Di) = 0 (i = 2, . . ., n). После проведения полного диагностического обследования энтропия (неопределенность) системы

H(D/K) = 0. (23.2)

Внесенная информация, содержащаяся в диагностическом обследовании, или диагностическая ценность обследования

JD (К) = ZD (К) = H(D)-H (D/K) = Н (D). (23.3)

В действительности, условие (23.2) удается выполнить далеко не всегда. Во многих случаях распознавание носит статистический характер и необходимо знать, что вероятность одного из состояний достаточно высока [например, P(D1)=0,95]. Для подобных ситуаций «остаточная» энтропия системы Н(D/К)0.

В практических случаях необходимая диагностическая ценность обследования

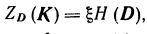(23.4)

где —коэффициент полноты обследования, 0 < < 1.

Коэффициент зависит от надежности распознавания и для реальных диагностических процессов должен быть близок единице. Если априорные вероятности состояний системы неизвестны, то всегда можно дать верхнюю оценку энтропии системы

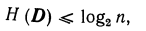, (23.5)

где п — число состояний системы.

Из условия (23.4) вытекает, что объем информации, которую необходимо получить при диагностическом обследовании, является заданным и требуется построить оптимальный процесс его накопления.

Условия оптимальности. При построении диагностического процесса следует учесть сложность получения соответствующей информации. Назовем коэффициентом оптимальности диагностического обследования по признаку kf для диагноза Di величину

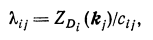(23.6)

где ZD. (kj) — диагностическая ценность обследования по признаку k1 для диагноза D. В общем случае

ZDi (kj) определяется с учетом результатов предыдущих обследований;

cif — коэффициент сложности обследования по признаку k} для диагноза D, характеризующий трудоемкость и стоимость обследования, его достоверность, длительность и другие факторы. Предполагается, что cif не зависит от проведенных ранее обследований.

Коэффициент оптимальности обследования для всей системы диагнозов

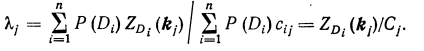(23.7)

Коэффициент оптимальности будет наибольшим, если необходимая величина диагностической ценности получается при наименьшем числе отдельных обследований. В общем случае оптимальный диагностический процесс должен обеспечить получение наибольшего значения коэффициента оптимальности всего обследования (условие оптимальности диагностического обследования).

 Домашнее задание: § конспект.

Закрепление материала:

Вопросы для самоконтроля

1. Что назввают простым признаком?
2. Что назввают сложным признаком?
3. К чему приводит использование неинформативных признаков
4. Объясните как обозначается простой признак.
5. Что называется сложным признаком?
6. Одноразрядный Двухразрядный Трехразрядный признаки – дайте им определение.
7. В чем заключена диагностическая ценность обследования, как она вычисляется?
8. Что делать для упрощения анализа на интервале?
9. Чем измеряется диагностическая ценность обследования по комплексу признаков для всей системы диагнозов?
10. С чем связан выбор наиболее информативных признаков для описания объекта?
11. Дайте описание коэффициента оптимальности.

Литература:

Амренов С. А. «Методы контроля и диагностики систем и сетей связи» КОНСПЕКТ ЛЕКЦИЙ -: Астана, Казахский государственный агротехнический университет, 2005 г.

И.Г. Бакланов Тестирование и диагностика систем связи. - М.: Эко-Трендз, 2001. Стр. 221-254

Биргер И. А. Техническая диагностика.— М.: «Машиностроение», 1978.—240,с, ил.

АРИПОВ М.Н , ДЖУРАЕВ Р.Х., ДЖАББАРОВ Ш.Ю. «ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ЦИФРОВЫХ СИСТЕМ» -Ташкент, ТЭИС, 2005

Платонов Ю. М., Уткин Ю. Г. Диагностика, ремонт и профилактика персональных компьютеров. -М.: Горячая линия - Телеком, 2003.-312 с: ил.

М.Е.Бушуева, В.В.Беляков Диагностика сложных технических систем Труды 1-го совещания по проекту НАТО SfP-973799 Semiconductors. Нижний Новгород, 2001

Малышенко Ю.В. ТЕХНИЧЕСКАЯ ДИАГНОСТИКА часть I конспект лекций

Платонов Ю. М., Уткин Ю. Г.Диагностика зависания и неисправностей компьютера/Серия «Техномир». Ростов-на-Дону: «Феникс», 2001. — 320 с.

PAGE \* MERGEFORMAT7

Диагностическая ценность признаков