Основы теории информации

Лекция 15

Тема. Основы теории информации.

Цель. Дать понятие о основах теории информации.

Учебная. Разъяснить измерения информации.

Развивающая. Развивать логическое мышление и естественное - научное мировоззрение.

Воспитательная. Воспитывать интерес к научным достижениям и открытиям в отрасли телекоммуникации.

Межпредметные связи:

Обеспечивающие: информатика, математика, вычислительная техника и МП, системы программирования.

Обеспечиваемые: Стажерская практика

Методическое обеспечение и оборудование:

Методическая разработка к занятию.

Учебный план.

Учебная программа

Рабочая программа.

Инструктаж по технике безопасности.

Технические средства обучения: персональный компьютер.

Обеспечение рабочих мест:

  • Рабочие тетради

Ход лекции.

Организационный момент.

Анализ и проверка домашней работы

Ответьте на вопросы:

Опишите основной параметр эффективности работы цифровой радиочастотной системы передачи.

Чем отличается измерение радиочастотных трактов от тракты спутниковых систем связи?

Что включает в себя измерения шумов?

Какие существует методы измерения ГВЗ?

К каким нежелательным эффектам приводит нарушение линейности радиочастотных трактов?

Что определяет амплитудно-частотная характеристика ретрансляторов?

Поясните принцип построения и работы систем радиоконтроля локального назначения.

Поясните принцип построения и работы систем радиоконтроля областного и местного значения.

Какие задачи должна решить подсистема мониторинга спектра?

Какие задачи должна решить подсистема управления спектром ?

Перечислите тнденции в использовании радиочастотного ресурса.

Как различают системы в зависимости от региона охвата?

Приведите структурную схему цифровой первичной сети, использующей радиочастотные средства.

Что является основным параметром для измерения работы усилителей ?К чему приводит перегрузка?

В каком случае «закрывается» глаз глазковой диаграммы?

К чему привоит высокий уровень шумов ?Как это выражается на глазковой диаграмме ?

Н а что вляет джиттер?

Привелите параметры антенны какие из них являются наиболее важными для эксплуатации ?

Для каких целей проводятся комплексные измерения радиочастотных трактов?

Какие выводы помогает сделать спектральный анализ?

В каких случаях используют частотомер и измеритель мощности, как проводятся эти измерения?

Какие методы измерения зависимости BER существуют в современной практике? Приведите из описание.

Что включает подсистема управления спектром и подсистема мониторинга спектра?

План лекции

1. Энтропия системы

2. Определение по Шеннону

2.1 Определение с помощью собственной информации

2.2 Свойства

2.3 Математические свойства

2.4 Эффективность

3. Условной энтропией

4. Взаимная энтропия

5. Энтропия сложной системы

  1. Измерение информации

6.1 Подходы к измерению информации

6.1.1 Содержательный подход

6.1.2 Алфавитный подход

  1. Единицы измерения информации

7.1 Структурный подход к измерению информации

7.2 Геометрическая мера

7.3 Комбинаторная мера

  1. Аддитивная мера

8. Неизмеряемость информации в быту (информация как новизна)

8.1 II ПОДХОД - объемный. Измерение информации в технике 

8.2 III ПОДХОД - вероятностный. Измерение информации в теории информации  (информация как  снятая неопределенность)

В технической диагностике, особенно при построении оптимальных диагностических процессов, широко используется теория информации. Возникшая как математическая теория связи в трудах Винера и Шеннона, теория информации получила применение и в других областях науки как общая теория связи статистических систем.

В Диагностике такими системами являются система состояний (диагнозов) и связанная с ней система признаков.

Центральное место в теории информации занимает понятие энтропии системы.

1.ЭНТРОПИЯ СИСТЕМЫ

Энтропия (от др.-греч.  — поворот, превращение) — в информатике — степень неполноты, неопределённости знаний. Явление, обратное энтропии, именуется негэнтропией.

Информационная энтропия — мера неопределённости или непредсказуемости информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения.

Например, в последовательности букв, составляющих какое-либо предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределённость появления для некоторых букв меньше, чем для других. Если же учесть, что некоторые сочетания букв (в этом случае говорят об энтропии n-го порядка, ) встречаются очень редко, то неопределённость уменьшается еще сильнее.

Энтропия — это количество информации, приходящейся на одно элементарное сообщение источника, вырабатывающего статистически независимые сообщения.

Информационная двоичная энтропия для независимых случайных событий x  с n возможными состояниями (от 1  до , n,p  — функция вероятности) рассчитывается по формуле

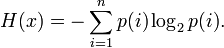
Эта величина также называется средней энтропией сообщения. Величина 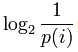 называется частной энтропией, характеризующей только -e состояние.

Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i , умноженных на их же двоичные логарифмы. Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

2. Определение по Шеннону

Клод Шеннон предположил, что прирост информации равен утраченной неопределённости, и задал требования к её измерению:

  1. мера должна быть непрерывной; то есть изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение функции;
  2. в случае, когда все варианты (буквы в приведённом примере) равновероятны, увеличение количества вариантов (букв) должно всегда увеличивать значение функции;
  3. должна быть возможность сделать выбор (в нашем примере букв) в два шага, в которых значение функции конечного результата должно являться суммой функций промежуточных результатов.

Поэтому функция энтропии 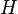должна удовлетворять условиям

  1. определена и непрерывна для всех 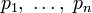, где 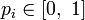для всех 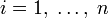и 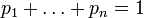. (Нетрудно видеть, что эта функция зависит только от распределения вероятностей, но не от алфавита.)
  2. Для целых положительных 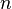, должно выполняться следующее неравенство:

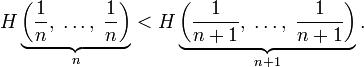
  1. Для целых положительных 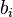, где 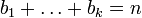, должно выполняться равенство

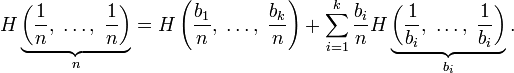
Шеннон показал,что единственная функция, удовлетворяющая этим требованиям, имеет вид

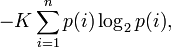
где 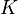 — константа (и в действительности нужна только для выбора единиц измерения).

Шеннон определил, что измерение энтропии (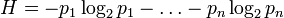), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надёжной передачи информации в виде закодированных двоичных чисел. Мера энтропии Шеннона выражает неуверенность реализации случайной переменной. Таким образом, энтропия является разницей между информацией, содержащейся в сообщении, и той частью информации, которая точно известна (или хорошо предсказуема) в сообщении. Примером этого является избыточность языка — имеются явные статистические закономерности в появлении букв, пар последовательных букв, троек и т. д.

2.1 Определение с помощью собственной информации

Также можно определить энтропию случайной величины, введя предварительно понятия распределения случайной величины 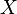, имеющей конечное число значений:

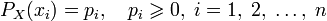
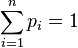
и собственной информации:

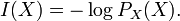
Тогда энтропия определяется как:

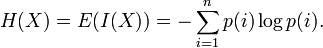
От количества возможных состояний 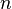случайной величины 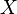зависит единица измерения количества информации и энтропии: бит, нат (Определяется через натуральный логарифм, в отличие от других единиц, где основание логарифма является целым числом. Нат равен log2e  1,443 бит)., трит (1 трит (трор) = log3(3 [возможных состояний (кодов)])).
От основания логарифма зависит числовая величина единицы измерения количества информации и энтропии.

2.2 Свойства

Энтропия является количеством, определённым в контексте вероятностной модели для источника данных. Например, кидание монеты имеет энтропию:

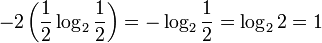бит на одно кидание (при условии его независимости), а количество возможных состояний равно: 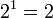возможных состояния (значения) ("орёл" и "решка").

У источника, который генерирует строку, состоящую только из букв «А», энтропия равна нулю: 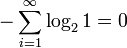, а количество возможных состояний равно: 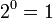возможное состояние (значение) («А») и от основания логарифма не зависит.
Это тоже информация, которую тоже надо учитывать. Примером запоминающих устройств в которых используются разряды с энтропией равной нулю, но с количеством информации равным 1 возможному состоянию, т.е. не равным нулю, являются разряды данных записанных в ПЗУ, в которых каждый разряд имеет только одно возможное состояние.

Так, например, опытным путём можно установить, что энтропия английского текста равна 1,5 бит на символ, что конечно будет варьироваться для разных текстов. Степень энтропии источника данных означает среднее число битов на элемент данных, требуемых для её зашифровки без потери информации, при оптимальном кодировании.

  • Некоторые биты данных могут не нести информации. Например, структуры данных часто хранят избыточную информацию, или имеют идентичные секции независимо от информации в структуре данных.
  • Количество энтропии не всегда выражается целым числом битов.

2.3 Математические свойства

  1. Неотрицательность: .
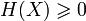  2. Ограниченность: 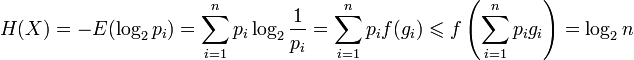, что вытекает из неравенства Йенсена для вогнутой функци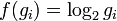и и 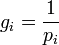. Если все 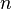элементов из 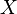равновероятны, .
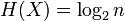  3. Если 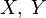независимы, то .
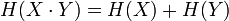  4. Энтропия — выпуклая вверх функция распределения вероятностей элементов.
  5. Если 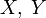имеют одинаковое распределение вероятностей элементов, то .

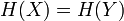2.4 Эффективность

Алфавит может иметь вероятностное распределение далекое от равномерного. Если исходный алфавит содержит 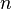символов, тогда его можно сравнить с «оптимизированным алфавитом», вероятностное распределение которого равномерное. Соотношение энтропии исходного и оптимизированного алфавита — это эффективность исходного алфавита, которая может быть выражена в процентах. Эффективность исходного алфавита с 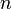символами может быть также определена как его 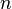-арная энтропия.

Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — типичного набора или, арифметического кодирования.

  1. Условной энтропией первого порядка (аналогично для Марковской модели первого порядка) называется энтропия для алфавита, где известны вероятности появления одной буквы после другой (то есть, вероятности двухбуквенных сочетаний):

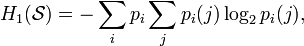
где 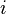 — это состояние, зависящее от предшествующего символа, и  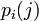— это вероятность 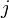при условии, что 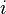был предыдущим символом.

Например, для русского языка без буквы «ё»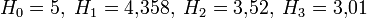

  1. Взаимная энтропия

Взаимная энтропия или энтропия объединения предназначена для расчёта энтропии взаимосвязанных систем (энтропии совместного появления статистически зависимых сообщений) и обозначается 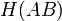, где 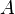характеризует передатчик, а  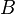— приёмник.

Взаимосвязь переданных и полученных сигналов описывается вероятностями совместных событий 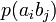, Для более общего случая, когда описывается не канал, а в целом взаимодействующие системы, матрица необязательно должна быть квадратной. Очевидно сумма всех элементов матрицы равна 1. Совместная вероятность 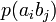событи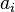й и 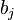вычисляется как произведение исходной и условной вероятности:

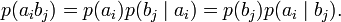
  1. Энтропия сложной системы 

Энтропия сложной системы  равна сумме энтропии всех ее однородных частей.

Энтропия сложной системы, объединяющей две статистически независимые системы, равна сумме энтропии этих систем. Так как энтропия системы неотрицательная величина, то при объединении систем энтропия возрастает или остается прежней. 

Энтропия сложной системы, объединяющей две статистически зависимые системы. Теперь вероятность того или иного состояния системы В будет зависеть от состояния, в котором находится система А. Так как зависимость систем - свойство взаимное, то подобное утверждение относится и к системе А. В рассматриваемом примере этс означает, что при сборке для сохранения постоянства зазора втулки больших размеров сочетаются с валиками больших размеров, а не с валиками произвольных размеров, как в предыдущем случае. Такая сборка называется селективной. 

Энтропия сложной системы равна сумме энтропии всех ее однородных частей. Поскольку все реальные процессы необратимы, энтропия изолированной системы может только возрастать, достигая максимума в состоянии термодинамического равновесия системы. 

Энтропия сложной системы равна сумме энтропии ее частей. 

Энтропия сложной системы, будучи аддитивным свойством, равна сумме энтропии ее составляющих.

Известно, что энтропия сложной системы, полученной объединением нескольких независимых систем, равна сумме энтропии последних

Конечно, можно просто определить энтропию сложной системы как сумму энтропии ее частей, независимо от того, находятся они в равновесии друг с другом или нет. Трудность состоит не в этом. Она заключается в том, что заранее не видно, идет ли такое определение в направлении раскрытия содержания истинного понятия энтропии. Понятия не строятся произвольно, а угадываются так, чтобы они наилучшим образом отражали действительные закономерности. Если мы подозреваем, что энтропия растет при всяком необратимом переходе в равновесие, и именно в с этим предполагаемым свойством стремимся определить ее для неравновесных состояний, то сделав это, мы сейчас же должны выяснить, сохраняется ли при новом определении предполагаемое свойство возрастания. 

Применяя теорему умножения вероятностей, доказывают, что энтропия сложной системы, состоящей из двух или нескольких независимых простых систем, равна сумме энтропии этих простых систем. Нельзя ли считать, что сумма этих энтропии и есть энтропия сложной системы, хотя сложная система и не находится в равновесии. 

  1. Измерение информации

6.1 Подходы к измерению информации

Как измерить информацию? Часто мы говорим, что, прочитав статью в журнале или просмотрев новости, не получили никакой информации, или наоборот, краткое сообщение может оказаться для нас информативным. В то же время для другого человека та же самая статья может оказаться чрезвычайно иноформативной, а сообщение — нет. Информативными сообщения являются тогда, когда они новы, понятны, своевременны, полезны. Но то, что для одного понятно, для другого — нет. То, что для одного полезно, ново, для другого — нет. В этом проблема определения и измерения информации.

При всем многообразии подходов к определению понятия информации, с позиции измерения информации нас будут интересовать два из них: определение К. Шеннона, применяемое в математической теории информации (содержательный подход), и определение А. Н. Колмогорова, применяемое в отраслях информатики, связанных с использованием компьютеров (алфавитный подход).

6.1.1 Содержательный подход

Согласно Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией — той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации.

По Шеннону, информация — уменьшение неопределенности наших знаний.

Неопределенность некоторого события — это количество возможных исходов данного события.
Так, например, если из колоды карт наугад выбирают карту, то неопределенность равна количеству карт в колоде. При бросании монеты неопределенность равна 2.

Содержательный подход часто называют субъективным, так как разные люди (субъекты) информацию об одном и том же предмете оценивают по-разному.

Но если число исходов не зависит от суждений людей (случай бросания кубика или монеты), то информация о наступлении одного из возможных исходов является объективной.

Если сообщение уменьшило неопределеность знаний ровно в два раза, то говорят, что сообщение несет 1 бит информации.

1 бит — объем информации такого сообщения, которое уменьшает неопределенность знания в два раза.

Рассмотрим, как можно подсчитать количество информации в сообщении, используя содержательный подход.

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных (равновозможных) событий. Тогда количество информации i, заключенное в этом сообщении, и число событий N связаны формулой:

2i = N. Эта формула носит название формулы Хартли. Получена она в 1928 г. американским инженером Р. Хартли.

Если N равно целой степени двойки (2, 4, 8, 16 и т.д.), то вычисления легко произвести "в уме". В противном случае количество информации становится нецелой величиной, и для решения задачи придется воспользоваться таблицей логарифмов либо определять значение логарифма приблизительно (ближайшее целое число, большее).

Например, если из 256 одинаковых, но разноцветных шаров наугад выбрали один, то сообщение о том, что выбрали красный шар несет 8 бит информации (28=256).
Для угадывания числа (наверняка) в диапазоне от 0 до 100, если разрешается задавать только двоичные вопросы (с ответом "да" или "нет"), нужно задать 7 вопросов, так как объем информации о загаданном числе больше 6 и меньше 7 (26<100>27)

6.1.2 Алфавитный подход

Алфавитный подход основан на том, что всякое сообщение можно закодировать с помощью конечной последовательности символов некоторого алфавита.

Алфавит — упорядоченный набор символов, используемый для кодирования сообщений на некотором языке.

Мощность алфавита — количество символов алфавита.
Двоичный алфавит содержит 2 символа, его мощность равна двум. Сообщения, записанные с помощью символов ASCII, используют алфавит из 256 символов. Сообщения, записанные по системе UNICODE, используют алфавит из 65 536 символов.

С позиций computer science носителями информации являются любые последовательности символов, которые хранятся, передаются и обрабатываются с помощью компьютера. Согласно Колмогорову, информативность последовательности символов не зависит от содержания сообщения, алфавитный подход является объективным, т.е. он не зависит от субъекта, воспринимающего сообщение. Чтобы определить объем информации в сообщении при алфавитном подходе, нужно последовательно решить задачи:

Определить количество информации (i) в одном символо по формуле 2i = N, где N — мощность алфавита

Определить количество символов в сообщении (m)

Вычислить объем инофрмации по формуле: V = i * m.

Например, если текстовое сообщение, закодированное по системе ASCII, содержит 100 символов, то его информационный объем составляет 800 бит.
Для двоичного сообщения той же длины информационный объем составляет 100 бит. В компьютерной технике бит соответствует физическому состоянию носителя информации: намагничено — не намагничено, есть отверстие — нет отверстия. При этом одно состояние принято обозначать цифрой 0, а другое — цифрой 1.

  1. Единицы измерения информации

Количество информации  - это мера уменьшения неопределенности.

В технике (теория кодирования и передачи сообщений) под количеством информации понимают количество кодируемых, передаваемых или хранимых символов.

Бит - двоичный знак двоичного алфавита {0, 1}.

Бит- минимальная единица измерения информации.

Байт - единица количества информации в системе СИ.

Байт - это восьмиразрядный двоичный код, с помощью которого можно представить один символ.

Единицы измерения информации в вычислительной технике

1 бит

 

 

1 байт

= 8 бит

 

1 Кбайт (килобайт)

= 210 байт = 1024 байт

~ 1 тысяча байт

1 Мбайт (мегабайт)

= 210 Кбайт = 220 байт

~ 1 миллион байт

1 Гбайт (гигабайт)

= 210 Мбайт = 230 байт

~ 1 миллиард байт

Информационный объем сообщения (информационная емкость сообщения) - количество информации в сообщении, измеренное в битах, байтах или производных единицах (Кбайтах, Мбайтах и т.д.).

 В информатике, как правило, измерению подвергается информация, представленная дискретным сигналом. При этом различают следующие подходы:

структурный. Измеряет количество информации простым подсчетом  информационных элементов, составляющих сообщение. Применяется для оценки возможностей запоминающих устройств, объемов передаваемых сообщений, инструментов кодирования без учета статистических характеристик их эксплуатации.

статистический. Учитывает вероятность появления сообщений: более информативным считается то сообщение, которое менее вероятно, т.е. менее всего ожидалось. Применяется при оценке значимости получаемой информации.

семантический. Учитывает целесообразность и полезность информации. Применяется при оценке эффективности получаемой информации и ее соответствия реальности.

7.1 Структурный подход к измерению информации

В рамках структурного подхода выделяют три меры информации:

геометрическая. Определяет максимально возможное количество информации в заданных объемах. Мера может быть использована для определения информационной емкости памяти компьютера;

комбинаторная. Оценивает возможность представления информации при помощи различных комбинаций информационных элементов в заданном объеме. Комбинаторная мера может использоваться для оценки информационных возможностей некоторого системы кодирования;

аддитивная, или мера Хартли.

7.2 Геометрическая мера

Определяет максимально возможное количество информации в заданных объемах. Единица измерения – информационный элемент. Мера может быть использована для определения информационной емкости памяти компьютера. В этом случае в качестве информационного элемента выступает минимальная единица хранения – бит. Список самых распространенных более крупных единиц и соотношение между ними приведено ниже:

8 бит = 1 байт (сокращенно б или Б),

1024 Б = 1 килобайт (сокращенно Кб или К),

1024 К = 1 мегабайт (сокращенно Мб или М),

1024 М = 1 гигабайт (сокращенно Гб или Г).

Тогда, например, объем винчестера – 3 гигабайта; объем основной памяти компьютера – 32 мегабайта и т.д.

Пример 1. Пусть сообщение  

5555 6666 888888

закодировано одним из специальных методов эффективного кодирования – кодирование повторений – и имеет вид:

5(4) 6(4) 8(6)        .        

Требуется измерить информацию в исходном и закодированном сообщениях геометрической мерой и оценить эффективность кодирования.

В качестве информационного элемента зададимся символом сообщения. Тогда:

I(исх.) = l(исх.) = 14 символов;

I(закод.) = l(закод.) = 12 символов,

где I(исх.), I(закод.) – количества информации, соответственно, в исходном и закодированном сообщениях;

l(исх.), l(закод.) – длины (объемы) тех же сообщений, соответственно.

Эффект кодирования определяется как разница между I(исх.)  и I(закод.) и составляет 2 символа.

Очевидно, геометрическая мера не учитывает, какими символами заполнено сообщение. Так, одинаковыми по количеству информации, измеренной геометрической мерой, являются, например, сообщения «компьютер» и «программа»; а также 346 и 10В.

7.3 Комбинаторная мера

Оценивает возможность представления информации при помощи различных комбинаций информационных элементов в заданном объеме. Использует типы комбинаций элементов и соответствующие математические соотношения, которые приводятся в одном из разделов дискретной математики – комбинаторике.

Комбинаторная мера может использоваться для оценки информационных возможностей некоторого автомата, который способен генерировать дискретные сигналы (сообщения) в соответствии с определенным правилом комбинаторики.

Комбинаторная мера используется для определения возможностей кодирующих систем, которые широко используются в информационной технике.

Пример 1. Определить емкость ASCII-кода, представленного в двоичной или шестнадцатеричной системе счисления.

ASCII-код – это сообщение, которое формируется как размещение с повторениями:

для двоичного представления – из информационных элементов {0, 1}, сообщение длиной (объемом) 8 символов;

для шестнадцатеричного представления – из информационных элементов {0, 1, 2, …., А, В, С, …. F}, сообщение длиной (объемом) 2 символа.

Тогда в соответствии с положениями комбинаторики:

I(двоичное) = РП(28) = 28 = 256;

I(шестнадцатеричное) = РП(162) = 162 = 256,

где I(двоичное), I(шестнадцатеричное) – количества информации, соответственно, для двоичного и шестнадцатеричного представления ASCII-кода.

Таким образом, емкость ASCII-кода для двоичного и шестнадцатеричного представления одинакова и равна 256.

Следует отметить, что все коды постоянной длины формируются по правилам комбинаторики или их комбинациям.

В случае, когда сообщения формируются как размещения с повторениями из элементов алфавита мощности h и известно количество сообщений М, можно определить требуемый объем сообщения (т.е.его длину l) для того, чтобы в этом объеме представить все сообщения: l = log hМ.

Например, есть 4 сообщения – a, b, c, d. Выполняется двоичное кодирование этих сообщений кодом постоянной длины. Для этого требуются 2 двоичных разряда. В самом деле: l = log 2 4  = 2.

Очевидно, комбинаторная мера является развитием геометрической меры, так как помимо длины сообщения учитывает объем исходного алфавита и правила, по которым из его символов строятся сообщения.

Особенностью комбинаторной меры является то, что ею измеряется информация не конкретного сообщения, а всего множества сообщений, которые могут быть получены.

Единицей измерения информации в комбинаторной мере является число комбинаций информационных элементов.

7.4 Аддитивная мера

Эта мера предложена в 1928 году американским ученым Хартли, поэтому имеет второе название – мера Хартли. Хартли впервые ввел специальное обозначение для количества информации – I и предложил следующую логарифмическую зависимость между количеством информации и мощностью исходного алфавита:

I = l log2 h,        

где I – количество информации, содержащейся в сообщении;

l – длина сообщения;

h – мощность исходного алфавита.

При исходном алфавите {0,1}; l = 1; h = 2 и основании логарифма, равном 2, имеем

I = 1*log22 = 1.

Данная формула даёт аналитическое определение бита (BIT - BInary digiT) по Хартли: это количество информации, которое содержится в двоичной цифре.

Единицей измерения информации в аддитивной мере является бит.

Пример 1. Рассчитать количество информации, которое содержится в шестнадцатеричном и двоичном представлении ASCII-кода для числа 49.

В соответствии с таблицей ASCII-кодов имеем: шестнадцатеричное представление числа 49 – 31, двоичное представление числа 49 – 00110001.        

Тогда по формуле Хартли получаем:

для шестнадцатеричного представления        I = 2log216 = 8 бит;

для двоичного представления                I = 8 log22 = 8 бит.

Таким образом, разные представления ASCII-кода для одного символа содержат одинаковое количество информации, измеренной аддитивной мерой.



Верно ли, что истрепанная книжка, если в ней нет вырванных страниц, несет для Вас ровно столько же информации, сколько такая же новая?

Каменная скрижаль весом в три тонны несет для археологов столько же информации, сколько ее хороший фотоснимок в археологическом журнале. Не так ли?

Когда московская радиостудия передает последние известия, то одну и ту же информацию получает и подмосковный житель и житель Новосибирска. Но поток  энергии радиоволн в Новосибирске намного меньше, чем в Москве.

Следовательно, мощность сигнала, также как и  размер и вес носителя, не могут служить оценкой количества информации, переносимой сигналом.  Как же оценить это количество?

Из курса физики вы знаете, что прежде, чем измерять значение какой-либо физической величины, надо ввести единицу измерения. У информации тоже есть такая единица - бит, но смысл ее различен при разных подходах к определению понятия “информация”.

 

Задача1: Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном мешочке находится 50 белых, 25красных, 25 синих шариков

1) всего шаров 50+25+25=100

2) вероятности шаров 50/100=1/2, 25/100=1/4, 25/100=1/4

3)I= -(1/2 log21/2 + 1/4 log21/4 + 1/4 log21/4) = -(1/2(0-1) +1/4(0-2) +1/4(0-2)) = 1,5 бит

 

Количество информации достигает max значения, если события равновероятны, поэтому количество информации можно расcчитать  по формуле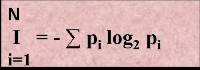 

Задача2 : В корзине лежит 16 шаров разного цвета. Сколько информации несет сообщение, что достали белый шар?

т.к. N = 16 шаров,  то  I = log2 N = log2 16 = 4 бит.

  1. Неизмеряемость информации в быту (информация как новизна)

ПРИМЕР

Вы получили какое - то сообщение, например, прочитали статью в любимом журнале. В этом сообщении содержится какое-то количество информации. Как оценить, сколько информации Вы получили? Другими словами, как измерить информацию? Можно ли сказать, что чем больше статья, тем больше информации она содержит?

Разные люди, получившие одно и то же сообщение, по-разному оценивают его информационную ёмкость, то есть количество информации, содержащееся в нем. Это происходит оттого, что  знания людей о событиях, явлениях, о которых идет речь в сообщении, до получения сообщения были различными. Поэтому те, кто знал об этом мало, сочтут, что получили много информации, те же, кто знал больше, могут сказать, что информации не получили вовсе. Количество информации в сообщении, таким образом, зависит от того, насколько ново это сообщение для получателя.

В таком случае, количество информации в одном и том же сообщении должно определяться отдельно для каждого получателя, то есть иметь субъективный характер. Но субъективные вещи не поддаются сравнению и анализу, для их измерения трудно выбрать одну общую для всех единицу измерения.

Таким образом, с точки зрения информации как новизны, мы не можем однозначно и объективно оценить количество информации, содержащейся даже в простом сообщении. Что же тогда говорить об измерении количества информации, содержащейся в научном открытии, новом музыкальном стиле, новой теории общественного развития.

Поэтому, когда информация рассматривается как новизна сообщения для получателя, не ставится вопрос об измерении количества информации.

8.1 II ПОДХОД - объемный. Измерение информации в технике (информация как сообщения в форме знаков или сигналов, хранимые, передаваемые и обрабатываемые с помощью технических устройств).

В технике, где информацией считается любая хранящаяся, обрабатываемая или передаваемая последовательность знаков, сигналов, часто используют простой способ определения количества информации, который может быть назван объемным. Он основан на подсчете числа символов в сообщении, то есть связан только с длиной сообщения и не учитывает его содержания.

Длина сообщения зависит от числа знаков, употребляемых для записи сообщения. Например, слово “мир” в русском алфавите записывается тремя  знаками, в английском - пятью (peace), а в КОИ -8 - двадцатью четырьмя битами (111011011110100111110010). 

ПРИМЕР

Исходное сообщение

Количество информации

на языке

в машинном представлении (КОИ - 8)

в символах

в битах

в байтах

рим

11110010 11101001 11101101

3

24

3

мир

11101101 11101001 11110010

3

24

3

миру мир!

11101101 11101001 11110010 11110101 00100000 11101101 1110101 11110010 00100001

9

72

9

(**  */

00101000 00101010 00101010 00100000 00101010 00101111

6

48

6

В вычислительной технике применяются две стандартные единицы измерения: бит (англ. binary digit - двоичная цифра) и байт (byte).

Конечно, будет правильно, если Вы скажете: “В слове “Рим” содержится 24 бита информации, а в сообщении  “Миру мир!” - 72 бита”. Однако, прежде, чем измерить информацию в битах, Вы определяете количество символов в этом сообщении. Нам привычней работать с символами, машине - с кодами. Каждый символ в настоящее время в вычислительной технике кодируется 8-битным или 16-битным кодом. Поэтому, для удобства была введена более “крупная” единица информации в технике (преимущественно в вычислительной) -байт. Теперь Вам легче подсчитать количество информации в техническом сообщении - оно совпадает с количеством символов в нем.

ПРИМЕР

В 100 Мб можно “уместить”:

страниц текста

50 000 или 150 романов

цветных слайдов высочайшего качества

150

аудиозапись речи видного политического деятеля

1.5 часа

музыкальный фрагмент качества CD -стерео

10 минут

фильм высокого качества записи

15 секунд

протоколы операций с банковским счетом

за 1000 лет

 

8.2 III ПОДХОД - вероятностный. Измерение информации в теории информации (информация как  снятая неопределенность)

Получение информации (ее увеличение) одновременно означает увеличение знания, что, в свою очередь, означает уменьшение незнания или информационной  неопределенности.

За единицу количества информации принимают выбор одного из двух  равновероятных  сообщений (“да” или “нет”, “1” или “0”). Она также названа бит. Вопрос ценности этой информации для получателя - это уже из иной области.

ПРИМЕР

Книга лежит на одной из двух полок - верхней или нижней. Сообщение о том, что книга лежит на верхней полке, уменьшает неопределенность ровно вдвое и несет 1 бит информации.

Сообщение о том, как упала монета после броска - “орлом” или “решкой”, несет один бит информации.

В соревновании участвуют 4 команды. Сообщение о том, что третья команда набрала большее количество очков, уменьшает первоначальную неопределенность ровно в четыре раза (дважды по два) и несет два бита информации.

Очень приближенно можно считать, что количество информации в сообщении о каком-то событии совпадает с количеством вопросов, которые необходимо задать и ответом на которые могут быть лишь “да” или “нет”, чтобы получить ту же информацию. Причем событие, о котором идет речь, должно иметь равновероятные исходы.

 ПРИМЕР

Сколько вопросов надо задать, чтобы отгадать одну из 32 карт (колода без шестерок), если ответами могут быть лишь “да” или “нет”?

Оказывается достаточно всего лишь 5 вопросов, но задавать их надо так, чтобы после каждого ответа можно было “отбрасывать” из рассмотрения ровно половину карт, среди которых задуманной не может быть. Такими , например, являются вопросы о цвете масти карты (“Задуманная карта красной масти?”), о типе карты (“Задуманная карта - “картинка”?”) и т.п.

То есть сообщение о том, какая карта из 32 задумана несет 5 бит информации.

Во всех приведенных примерах число равновероятных исходов события, о котором идет речь в сообщении, было кратным степени числа 2 (4 = 22, 32 = 25). Поэтому сообщение “несло” количество бит информации всегда было целым числом. Но в реальной практике могут встречаться самые разные ситуации.

ПРИМЕР

Сообщение о том, что на светофоре красный сигнал, несет в себе информации больше, чем бит. Попробуйте объяснить почему.

ПРИМЕР

Известно, что Иванов живет на улице Весенней. Сообщение о том, что номер его дома есть число четное, уменьшило неопределенность. Получив такую информацию, мы стали знать больше, но информационная неопределенность осталась, хотя и уменьшилась.

Почему в этом случае мы не можем сказать, что первоначальная неопределенность уменьшилась вдвое (иными словами, что мы получили 1 бит информации)? Если Вы не знаете ответа на этот вопрос, представьте себе улицу, на четной стороне которой, например, четыре дома, а на нечетной - двадцать. Такие улицы не такая уж большая редкость.

Последние примеры показывают, что данное выше определение количества информации слишком упрощено. Уточним его. Но прежде разберем еще один пример.

ПРИМЕР

Пылкий влюбленный, находясь в разлуке с объектом своей любви, посылает телеграмму: “Любишь?”. В ответ приходит не менее лаконичная телеграмма: “Да!”. Сколько информации несет ответная телеграмма? Альтернатив здесь две- либо Да, либо Нет. Их можно обозначить символами двоичного кода 1 и 0. Таким образом, ответную телеграмму можно было бы закодировать всего одним двоичным символом.

Можно ли сказать, что ответная телеграмма несет одну единицу информации?

Если влюбленный уверен в положительном ответе, то ответ “да” почти не даст ему никакой новой информации. То же самое относится и к безнадежно влюбленному, уже привыкшему получать отказы. Ответ “нет” также принесет ему очень мало информации. Но внезапный отказ уверенному влюбленному (неожиданное огорчение) или ответ “да” безнадежному влюбленному (нечаянная радость) несет сравнительно много информации, настолько много, что радикально изменяется все дальнейшее поведение влюбленного, а, может быть, его судьба!

Таким образом, с точки зрения на информацию как на снятую неопределенность количество информации зависит от вероятности получения данного сообщения. Причем, чем больше вероятность события, тем меньше количество информации в сообщении о таком событии.

Иными словами, количество информации в сообщении о каком-то событии зависит от вероятности свершения данного события.

Научный подход к оценке сообщений был предложен еще в 1928 году Р.Хартли. Расчетная формула имеет вид:

I = log2 N   или   2I = N,

где       N - количество равновероятных событий (число возможных выборов),

            I - количество информации.

Если N = 2 (выбор из двух возможностей), то I = 1 бит.

Бит выбран в качестве единицы количества информации потому, что принято считать, что двумя двоичными словами исходной длины k или словом длины 2k можно передать в 2 раза больше информации, чем одним исходным словом. Число возможных равновероятных выборов при этом увеличивается в 2k раз, тогда как I удваивается.

Иногда формула Хартли записывается иначе. Так как наступление каждого из N возможных событий имеет одинаковую вероятность  p = 1 / N, то N = 1 / p и формула имеет вид

I = log2 (1/p) = - log2 p

Пусть имеется строка текста, содержащая тысячу букв. Буква “о” в тексте встречается примерно 90 раз, буква ”р” ~ 40 раз, буква “ф” ~ 2 раза, буква “а” ~ 200 раз. Поделив 200 на 1000, мы получим величину 0.2, которая представляет собой среднюю частоту, с которой в рассматриваемом тексте встречается буква “а”. Вероятность появления буквы “а” в тексте (pa)можем считать приблизительно равной 0.2. Аналогично, pр = 0.04, pф = 0.002, ро = 0.09.

Далее поступаем согласно К.Шеннону. Берем двоичный логарифм от величины 0.2 и называем то, что получилось количеством информации, которую переносит одна-единственная бква “а” в рассматриваемом тексте. Точно такую же операцию проделаем для каждой буквы. Тогда количество собственной информации, переносимой одной буквой равно

hi = log2 1/pi = - log2 pi,

где pi - вероятность появления в сообщении i-го символа алфавита.

Удобнее в качестве меры количества информации пользоваться не значением hi , а средним значением количества информации, приходящейся на один символ алфавита

H = S pi hi = - S pi log2 pi

Значение Н достигает максимума при равновероятных событиях, то есть при равенстве всех pi

pi = 1 / N.

В этом случае формула Шеннона превращается в формулу Хартли.

В теории информации количеством информации называют числовую характеристику сигнала, которая не зависит от его формы и содержания и характеризует неопределенность, которая исчезает после получения сообщения в виде данного сигнала. В этом случае количество информации зависит от вероятности получения сообщения о том или ином событии.

Для абсолютно достоверного события (событие обязательно произойдет, поэтому его вероятность  равна 1) количество информации в сообщении о нем равно 0. Чем невероятнее событие, тем большее  количество информации несет сообщение о нем. Лишь при равновероятных ответах ответ “да” или “нет” несет один бит информации.

Количество информации при вероятностном подходе можно вычислить, пользуясь следующими формулами:

1). Формула Хартли.

I = log2 N   или   2I = N,

где       N - количество равновероятных событий (число возможных выборов),

            I - количество информации.

2). Модифицированная формула Хартли.

и формула имеет вид

I = log2 (1/p) = - log2 p

где       p - вероятность наступления каждого из N возможных равновероятных событий.

3). Формула Шеннона.

H = S pi hi = - S pi log2 pi

где       pi - вероятность появления в сообщении i-го символа алфавита;

            hi = log2 1/pi = - log2 pi -  количество собственной информации, переносимой одним символом;

            Н - среднее значением количества информации.

 Домашнее задание: § конспект.

Закрепление материала:

Вопросы для самоконтроля

  1. Что такое энтропия?
  2. Каие требования задал Клод Шенон к измерению информации ?
  3. Как связаны энтропия и пропускная способность канала?
  4. Приведите математические свойства энтропии.
  5. Что такое эффективность исходного алфавита?
  6. Что называется условной энтропией первого порядка ?
  7. Для чего предназначена взаимная энтропия или энтропия объединения?
  8. Чему равна энтропия сложной системы ?
  9. Что такое содержательный подход к измеению?
  10. Приведите формулу Хартли.дайте ей пояснение.
  11. Приведите формулу Хартли.
  12. На чем основан основан алфавитный подход, что такое мощность алфавита ?
  13. Что такое информация по  Шеннону? 
  14. Что такое количество информации , мера измерения?
  15. Дайте определение информационному объему сообщения, какие различают при этом подходы?
  16. Какие меры информации выделяют в рамках структурного подхода к измерению информации?
  17. Что определяет геометрическая мера измерения информации?
  18. Что определяет комбинаторная мера измерения информации?
  19. Что определяет аддитивная мера измерения информации?
  20. От чего зависит количество информации в сообщении?
  21. На чем основан объемный способ передачи последовательности знаков, сигналов?
  22. Что в теории информации  называют количеством информации?
  23. Какие подходы к измерению информации вам известны?
  24. Какова основная единица измерения информации?
  25. Сколько байт содержит 1 Кб информации?
  26. Приведите формулу подсчета количества информации при уменьшении неопределенности знания.
  27. Как подсчитать количество информации, передаваемое в символьном сообщении?

Литература:

Амренов С. А. «Методы контроля и диагностики систем и сетей связи» КОНСПЕКТ ЛЕКЦИЙ -: Астана, Казахский государственный агротехнический университет, 2005 г.

И.Г. Бакланов Тестирование и диагностика систем связи. - М.: Эко-Трендз, 2001. Стр. 221-254

Биргер И. А. Техническая диагностика.— М.: «Машиностроение», 1978.—240,с, ил.

АРИПОВ М.Н , ДЖУРАЕВ Р.Х., ДЖАББАРОВ Ш.Ю. «ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ЦИФРОВЫХ СИСТЕМ» -Ташкент, ТЭИС, 2005

Платонов Ю. М., Уткин Ю. Г. Диагностика, ремонт и профилактика персональных компьютеров. -М.: Горячая линия - Телеком, 2003.-312 с: ил.

М.Е.Бушуева, В.В.Беляков Диагностика сложных технических систем Труды 1-го совещания по проекту НАТО SfP-973799 Semiconductors. Нижний Новгород, 2001

Малышенко Ю.В. ТЕХНИЧЕСКАЯ ДИАГНОСТИКА часть I конспект лекций

Платонов Ю. М., Уткин Ю. Г.Диагностика зависания и неисправностей компьютера/Серия «Техномир». Ростов-на-Дону: «Феникс», 2001. — 320 с.

PAGE \* MERGEFORMAT 14

Основы теории информации